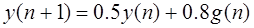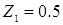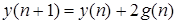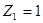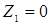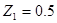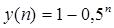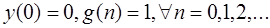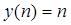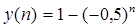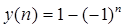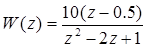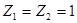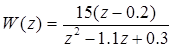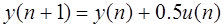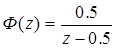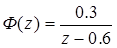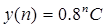Корни характеристического уравнения замкнутой системы равны степень устойчивости системы равна

2. Корневой критерий

3. Критерий Стодолы

4. Критерий Гурвица

5. Критерий Михайлова

6. Критерий Найквиста

7. Показатели качества

8. Прямые показатели качества

9. Корневые показатели качества

10. Частотные показатели качества

Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.

Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:

1) корневой критерий,

2) критерий Стодолы,

3) критерий Гурвица,

4) критерий Найквиста,

5) критерий Михайлова и др.

Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.

2. Корневой критерий

Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.

Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.

Виды корней характеристического уравнения:

положительные (корень № 1);

комплексные сопряженные (4);

По кратности корни бывают:

одиночные (1, 2, 3);

сопряженные (4, 5): s_i = a ± j w ;

Корневой критерий формулируется следующим образом:

Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.

Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.

Пример 4.1. Передаточная функция системы имеет вид:

.

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.

Следовательно, система устойчива.

3. Критерий Стодолы

Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.

То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.

4. Критерий Гурвица

Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.

W_p — передаточная функция регулятора,

W_y — передаточная функция объекта управления.

Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы): W _¥ = W_p W_y .

Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

.

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

.

Тогда после подстановки и преобразования получаем:

.

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W _¥ :

D _з( s ) = A ( s ) + B ( s ).

Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с a_{n +1} по a ₀. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a ₀, a ₂, a ₄… или a ₁, a ₃, a ₅ …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.

Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.

Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.

Пример. Дана передаточная функция разомкнутой системы

.

Требуется определить устойчивость замкнутой системы по критерию Гурвица .

Для этого определяется ХПЗС :

D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.

Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а₄ = 2, а₃ = 5, а₂ = 10, а₁ = 6, а₀ = 1.

Матрица имеет вид:

(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

,

Поскольку все определители положительны, то АСР устойчива.

5. Критерий Михайлова

Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

,

где t — запаздывание.

В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.

Порядок применения критерия Михайлова:

1) Записывается характеристическое выражение замкнутой системы:

D _з (s) = A(s) + B(s) . e — t s .

2) Подставляется s = j w : D _з (j w ) =Re( w ) + Im( w ).

3) Записывается уравнение годографа Михайлова D _з( j w ) и строится кривая на комплексной плоскости.

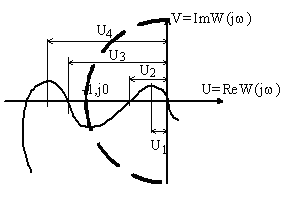
Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n — степень характеристического полинома.

Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.

6. Критерий Найквиста

Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.

1) Определяется передаточная функция разомкнутой системы .

2) Определяется число правых корней m .

3) Подставляется s = j w : W _¥ ( j w ).

4) Строится АФХ разомкнутой системы.

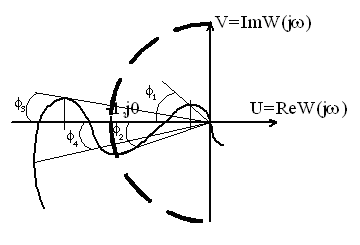
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W _¥ ( j w ) m раз охватывала точку (-1; 0), где m — число правых корней разомкнутой системы.

Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.

В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W _¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).

7. Показатели качества

Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.

Показатели качества разбиты на 4 группы:

1) прямые — определяемые непосредственно по кривой переходного процесса,

2) корневые — определяемые по корням характеристического полинома,

3) частотные — по частотным характеристикам,

4) интегральные — получаемые путем интегрирования функций.

8. Прямые показатели качества

К ним относятся: степень затухания y , перерегулирование s , статическая ошибка е_ст, время регулирования t_p и др.

Рис. 4.4

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).

Сразу по ней определяется установившееся значение выходной величины у_уст.

Степень затухания y определяется по формуле

,

где А₁ и А₃ — соответственно 1-я и 3-я амплитуды переходной кривой.

Перерегулирование s = , где y_max — максимум переходной кривой.

Статическая ошибка е_ст = х — у_уст, где х — входная величина.

Время достижения первого максимума t _м определяется по графику.

Время регулирования t_p определяется следующим образом: Находится допустимое отклонение D = 5% у_уст и строится «трубка» толщиной 2 D . Время t_p соответствует последней точке пересечения y ( t ) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.

9. Корневые показатели качества

К ним относятся: степень колебательности m , степень устойчивости h и др.

Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:

Степень устойчивости h определяется как граница, правее которой корней нет, т.е.

h = min ,

где Re ( s_i ) — действительная часть корня s_i .

Степень колебательности m рассчитывается через угол g : m = tg g . Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g — угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:

m = min .

10. Частотные показатели качества

Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.

По АФХ определяются запасы: D A — по амплитуде, D j — по фазе.

Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.

Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.

По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке М_Е как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.

Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:

; t_p = ; ; M = .

Корневой критерий

Корневой критерий позволяет определить устойчивость системы по корням характеристического уравнения. Характеристическое уравнение можно получить путем приравнивания знаменателя передаточной функции объекта или системы к нулю

Корни характеристического уравнения s, могут быть как действительные, так и комплексные. Их можно разместить на комплексной плоскости (рис. 95).

Корни характеристического уравнения могут быть:

• — действительными: положительными, отрицательными (2,6) или нулевыми (3);
• — комплексными: с положительными (корень 1), отрицательными (4) и нулевыми (5) действительными частями. В последнем случае корни (5) являются чисто мнимыми.

Рис. 95. Варианты расположение корней характеристического уравнения на комплексной плоскости

По кратности корни бывают одиночные и повторяющиеся.

Корневой критерий формулируется следующим образом. Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости (имеют отрицательные вещественные части). Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости, то не зависимо от числа корней в левой система является неустойчивой.

Чтобы корни характеристического уравнения имели отрицательные вещественные части, необходимо чтобы все его коэффициенты cij были положительны. Однако это условие является достаточным только для систем, описываемых ДУ 1-го и 2-го порядков. При п > 2 этого условия недостаточно.

Практическое использование корневого критерия рассмотрено в примере 8.

Пусть передаточная функция системы имеет вид

Её характеристическое уравнение

Так как все действительные корни и действительные части комплексных корней отрицательны, система устойчива.

Алгебраические критерии устойчивости

Под алгебраическими критериями устойчивости понимают условия, сформулированные для коэффициентов характеристического уравнения, при выполнении которых линейная система устойчива, а при невыполнении — неустойчива.

Наибольшее распространение среди алгебраических критериев устойчивости получил критерий Гурвица (немецкий математик Адольф Гурвиц, 1859 — 1919). К алгебраическим критериям относят также критерии Рауса (1877), Льенара—Шипара (1914) и др.

В основе критерия Гурвица лежит анализ коэффициентов характеристического уравнения динамической системы. Из коэффициентов характеристического уравнения

составляется матрица Г урвица, по диагонали которой от верхнего левого угла записываются по порядку все коэффициенты характеристического уравнения, начиная с а. Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз уменьшались

Определение критерия. Для устойчивости системы необходимо и достаточно чтобы главный определитель и все п диагональные миноры, получаемые из квадратной матрицы коэффициентов, были положительными при ао > 0.

Матрицы для расчета диагональных миноров получают из исходной путем последовательного включения столбцов и строк

Если хотя бы один определитель будет равен нулю, то система будет находиться на границе устойчивости.

Если хотя бы один определитель будет отрицателен, то система неустойчива, не зависимо от числа положительных или нулевых определителей.

Вычисление диагональных миноров невысоких порядков (Д. Д₅) не представляет значительного труда, и устойчивость конкретной системы может быть легко определена вручную (пример 9).

Дана передаточная функция замкнутой системы

Требуется определить устойчивость замкнутой системы по критерию Гурвица.

Для этого по знаменателю передаточной функции записывается характеристическое уравнение замкнутой системы

Поскольку максимальная степень характеристического уравнения замкнутой системы равна п = 4, то матрица Гурвица будет иметь размер 4×4.

Коэффициенты характеристического уравнения равны:

Определитель Гурвица имеет вид

Диагональные определители будут равны:

Поскольку все определители положительны и а₀ > 0, то АСР устойчива.

При исследовании устойчивости с помощью критерия Лье- нара-Шипара (Lienard, Chipard, 1914) нужно, прежде всего, проверить необходимое условие устойчивости. Если необходимое условие устойчивости выполняется, то для определения устойчивости, нет необходимости вычислять все определители Гурвица.

Определение критерия. При выполнении необходимого условия устойчивости (а₀ > 0, а >0. а_П > 0) для устойчивости

системы управления необходимо и достаточно, чтобы все ее определители Гурвица с четными индексами или все ее определители Гурвица с нечетными индексами были положительными:

Для формулировки критерия Рауса (Е. J. Routh, английский математик) составляется таблица Рауса следующим образом: в первой строке выписываются коэффициенты характеристического полинома с четными индексами, а во второй строке — коэффициенты с нечетными индексами в порядке их возрастания (табл. 6).

Таблица Рауса содержит n + 1 строку. Элементы последующих строк вычисляются по формулам:

Число столбцов по мере роста номера строки убывает. Элементы второго и последующих столбцов следует вычислять по мере надобности при вычислении элементов первого столбца. При этом вычисление можно прекратить, как только какой-либо элемент первого столбца принимает нулевое или отрицательное значение.

Определение критерия. Для того чтобы система была устойчива, необходимо и достаточно, чтобы все элементы первого столбца таблицы Рауса при а₀> 0 были положительны: Си > 0, к = 1,2. п+1.

Характеристическое уравнение замкнутой системы регулирования без запаздывания имеет вид:

Требуется определить устойчивость замкнутой системы по критерию Рауса. Составим таблицу Рауса (табл.7).

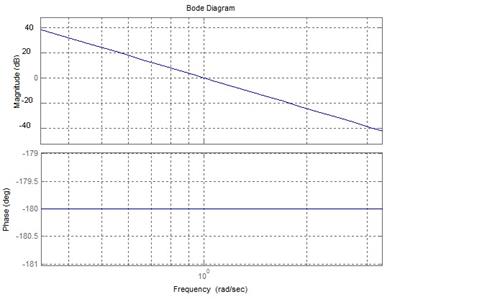
Цифровая система, описание которой задается передаточной функцией

Цифровая система, описание которой задается передаточной функцией

,

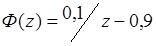
Правильный ответ:
устойчива. !Task 17

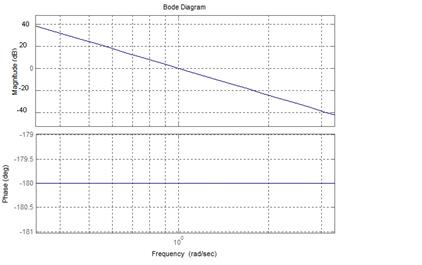
Цифровая система, описание которой задается передаточной функцией

,

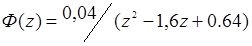
Правильный ответ:
устойчива. !Task 18

Цифровая система с единичной отрицательной обратной связью, описание разомкнутого контура которой задается передаточной функцией

,

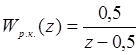
Правильный ответ:
устойчива.

Цифровая система с единичной отрицательной обратной связью, описание разомкнутого контура которой задается передаточной функцией

,

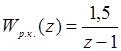
Правильный ответ:
устойчива.

3. Дидактическая единица ГОС: Цифровые системы управления

4. Тема задания: Математические модели дискретных (цифровых ) систем управления

!Task 1Порядок разностного уравненияy[(n+2)T] + 0,2y[nT] = 5 x[nT],где: T – период квантования времени, n = 0,1, … — дискретное время, равен … Правильный ответ:2.

!Task 2Порядок разностного уравненияy[(n+2)T] + 0,2y[nT] = 5 x[nT],где: T – период квантования времени, n = 0,1, … — дискретное время,равен … Правильный ответ:
2.

!Task 3Порядок разностного уравненияy[(n+1)T] + 0,2y[nT] = 5 x[(n-1)T],где: T – период квантования времени, n = 0,1, … — дискретное время,равен … Правильный ответ:
2.

!Task 4Порядок разностного уравненияy[(n+2)T] + 0,2y[(n+1)T] + y[nT] = x[nT] + 5 x[(n-1)T],где: T – период квантования времени, n = 0,1, … — дискретное время,равен … Правильный ответ:
3. !Task 5При условии, что Z – преобразование функции y[nT] равно Y(z), Z –преобразование функции y[(n+k)T] будет равно … Правильный ответ:
z k Y(z).

!Task 6Передаточная функция системы, описываемой разностным уравнениемy[(n+1)T] + 0,2y[nT] = 5 g[(n)T],где: T – период квантования времени, n = 0,1, … — дискретное время,равна … Правильный ответ:
5/(z + 0,2).

!Task 7Передаточная функция системы, описываемой разностным уравнениемy[(n+2)T] + 0,2y[nT] = 5 g[(n)T],где: T – период квантования времени, n = 0,1, … — дискретное время,равна … Правильный ответ:
5/(z 2 + 0,2).

!Task 8Передаточная функция системы, описываемой разностным уравнениемy[(n+1)T] = 0,2y[nT] + 5 g[(n)T],где: T – период квантования времени, n = 0,1, … — дискретное время, равна … Правильный ответ:
5/(z — 0,2).

!Task 10Передаточная функция системы, описываемой разностным уравнениемy[(n+1)T] = 10 g[(n)T],где: T – период квантования времени, n = 0,1, … — дискретное время, равна … Правильный ответ:
10/z .

Корни характеристического уравнения разностного уравнения

задающего описание движения цифровой системы управления, равен

Правильный ответ:

Корень характеристического уравнения разностного уравнения

задающего описание движения цифровой системы управления, равен …

Правильный ответ:

Корень характеристического уравнения разностного уравнения

,

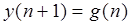
задающего описание движения цифровой системы управления, равен …

Правильный ответ:

Корень характеристического уравнения разностного уравнения

,

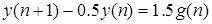
задающего описание движения цифровой системы управления, равен …

Правильный ответ:

Решение разностного уравнения

, ,

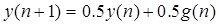
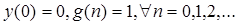
задающего описание движения цифровой системы управления при заданном начальном условии и постоянной вынуждающей функции будет иметь вид …

Правильный ответ:

Решение разностного уравнения

,

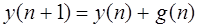
задающего описание движения цифровой системы управления при заданном начальном условии и постоянной вынуждающей функции будет иметь вид …

Правильный ответ:

Решение разностного уравнения

,

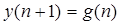
задающего описание движения цифровой системы управления при заданном начальном условии и постоянной вынуждающей функции будет иметь вид …

Правильный ответ:
y(n) = 1 — 0 n .

Решение разностного уравнения

,

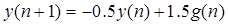
задающего описание движения цифровой системы управления при заданном начальном условии и постоянной вынуждающей функции будет иметь вид …

Правильный ответ:

Решение разностного уравнения

,

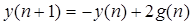
задающего описание движения цифровой системы управления при заданном начальном условии и постоянной вынуждающей функции будет иметь вид …

Правильный ответ:

Полюса передаточной функции цифровой системы

Правильный ответ:

Нули передаточной функции цифровой системы

Описание движения разомкнутого контура системы задается разностным уравнением

Передаточная функция замкнутой цифровой системы с единичной отрицательной обратной связью равна …

Правильный ответ:

Описание движения разомкнутого контура системы задается разностным уравнением

.

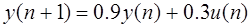
Передаточная функция замкнутой цифровой системы с единичной отрицательной обратной связью равна …

Правильный ответ:

!Task 24Командный генератор, описываемый разностным уравнением 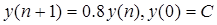воспроизводит внешние воздействия вида … Правильный ответ:

3. Дидактическая единица ГОС: Цифровые системы управления

4. Тема задания: Базовые понятия теории цифровых систем

Система автоматического управления, которая кроме звеньев, описываемых линейными дифференциальными уравнениями, содержит элементы с квантованием сигналов по времени, называется …

Правильный ответ:
дискретной.

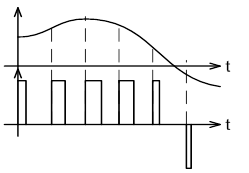
Входной и выходной сигналы импульсного элемента показаны на рисунке.

Такой вид модуляции сигнала называется …

Правильный ответ:
широтно-импульсной.

Если непрерывному изменению входного сигнала элемента на выходе соответствует последовательность импульсов одинаковой формы с равным интервалом дискретизация, амплитуда которых равна или пропорциональна значениям входного сигнала в дискретные моменты времени, то такая модуляция называется …

Правильный ответ:
амплитудно-импульсной.

Если на выходе элемента системы непрерывному изменению входного сигнала на выходе соответствует последовательность импульсов одинаковой формы, частота следования (интервал дискретизации) которых равна или пропорциональна значениям входного сигнала в дискретные моменты времени, то такая модуляция называется …

Правильный ответ:
частотно -импульсной.

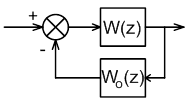
Структурная схема системы показана на рисунке.

Передаточная функция замкнутой системы равна …

Структурная схема системы показана на рисунке.

Передаточная функция замкнутой системы по ошибке равна …

Если элемент системы осуществляет амплитудно-импульсную модуляцию и непрерывному изменению входного сигнала на выходе соответствует последовательность импульсов прямоугольной формы длительностью равной интервалам дискретизации, амплитуда которых равна или пропорциональна значениям входного сигнала в дискретные моменты времени, то такой элемент называют …

Правильный ответ:
экстраполятор нулевого порядка.

Дискретное преобразование Лапласа используется для исследования …

Правильный ответ:
линейных дискретных систем.

Дискретное преобразование Лапласа позволяет получить связь дискретных изображений Лапласа выходной и входной переменных при нулевых начальных условиях в виде …

Правильный ответ:
передаточной функции.

Переходная функция есть реакция системы (элемента) при нулевых начальных условиях на воздействие вида …

Правильный ответ:
ступенчатого вида

3. Дидактическая единица ГОС: Анализ качества систем управления

4. Тема задания: Анализ качества с использованием частотных характеристик

!Task 1Показатель колебательности определяется по… Правильный ответ:
амплитудно-частотной характеристике замкнутой системы.

!Task 2Показатель колебательности равен …

Правильный ответ:
максимальному значению ординаты амплитудной характеристики замкнутой системы при начальной ординате, равной единице.

!Task 2Запас устойчивости по модулю замкнутой системы это …

Правильный ответ:
частотный показатель качества замкнутой системы, определяемый по амплитудной характеристике разомкнутой системы.

!Task 4Запас устойчивости по модулю замкнутой системы равен значению …

Правильный ответ:
значение логарифмической амплитудно-частотной характеристики разомкнутой системы, взятое с знаком минус, и вычисленное на частоте, на которой фазовый сдвиг равен –π.

!Task 5Запас устойчивости по фазе замкнутой системы определяется по …

фазовой характеристике разомкнутой системы.

!Task 6Запас устойчивости по фазе замкнутой системы вычисляется по значению …

Правильный ответ:
значению фазовой характеристики разомкнутой системы на частоте среза.

!Task 7Запас устойчивости по фазе у хорошо демпфированных систем составляет величину …

Правильный ответ:
величину 30°-60°.

!Task 8Запас устойчивости по модулю замкнутой системы у хорошо демпфированной системы составляет ______ дБ.

Правильный ответ:
6 – 20 дБ.

!Task 9Частота среза системы это …

Правильный ответ:
частотный показатель качества замкнутой системы, определяемый по амплитудной характеристике разомкнутой системы.

!Task 10Частота среза системы это …

Правильный ответ:
частота, на которой амплитудная характеристика разомкнутой системы равна 1.

!Task 11Запас устойчивости по модулю (амплитуде) системы равен …

!Task 12Запас устойчивости фазе равен …

!Task 13Запас устойчивости по фазе замкнутой системы, разомкнутый контур которой имеет передаточную функцию вида: W(s)=10/s будет равен…

!Task 14Частота среза системы с передаточной функцией разомкнутого контура

!Task 15Передаточная функция разомкнутой системы равна W(s)=100/s 2 . В этом случае частота среза системы равна _______ 1/с.

!Task 16Передаточная функция разомкнутой системы равна W(s)=10/s(0,1s+1). В этом случае частота среза системы, определяемая по асимптотической логарифмической частотной характеристике, равна _______ 1/с.

!Task 17Передаточная функция разомкнутой системы равна W(s)=25/s 2 . В этом случае частота среза системы равна _______ 1/с.

!Task 18Передаточная функция разомкнутой системы равна W(s)=10/(0,1s+1). В этом случае частота среза системы, определяемая по асимптотической логарифмической частотной характеристике, равна _______ 1/с.

!Task 19 При двукратном увеличении коэффициента передачи разомкнутой системы вида: W(s)=10/s(0,1s+1), частота среза системы …

Правильный ответ:
увеличится

!Task 20Увеличение частоты среза системы приводит к …

Правильный ответ:
увеличению быстродействия.

!Task 21Логарифмическая амплитудная характеристика разомкнутой системы на частоте ω=10 1/c проходит выше контрольной точки 20 дБ. Это означает, что амплитуда ошибки при гармоническом входном сигнале g(t) = G*sin(10t) …

Правильный ответ:
не больше G/10.

3. Дидактическая единица ГОС: Анализ качества систем управления

4. Тема задания: Анализ точности систем управления

!Task 1Значение установившейся ошибки в системе с нулевым порядком астатизма при постоянном входном воздействии можно уменьшить путем …

Правильный ответ:
путем увеличения коэффициента передачи разомкнутого контура системы.

!Task 2У системы с единичной обратной связью передаточная функция разомкнутого контура равнаW(s) = 3/(0.5s + 1) .Значение установившейся ошибки системы при входном воздействии g = 12 будет равно …

!Task 3Уменьшение коэффициента передачи разомкнутого контура статической системы приведет к увеличению …

Правильный ответ:
установившейся ошибки.

!Task 4У системы с единичной обратной связью передаточная функция разомкнутого контура равнаW(s) = 1/(5s + 1) .Значение установившейся ошибки системы при входном воздействии g = 10 равно …

!Task 5Значение установившейся ошибки у статической следящей системы с единичной обратной связью и передаточной функцией разомкнутого контура W(s) = 9/(0.1s + 1) при входном воздействии g(t) =10t равно …

!Task 6Передаточная функция разомкнутой системы равна W(s) = 10/s. Установившаяся ошибка системы, замкнутой единичной обратной связью, при входном воздействии g(t) = 20*t равна …

!Task 7У системы с единичной обратной связью передаточная функция разомкнутого контура равнаW(s) = К/(0.5s + 1) .Для обеспечения установившейся ошибки системы не боле 1 при входном воздействии g = 10 величину К следует выбрать не менее …

!Task 8У системы с единичной отрицательной обратной связью передаточная функция разомкнутого контура равнаW(s) = К/s .Для обеспечения минимальной установившейся ошибки системы при входном воздействии g = 10 величину К следует выбрать …

Правильный ответ:
больше 0.

3. Дидактическая единица ГОС: Точностные характеристики систем

4. Тема задания: Точностные характеристики систем

!Task 1Для вычисления ошибки слежения системы с единичной обратной связью, если W(s) – передаточная функция разомкнутой системы, Ф(s) = W(s)/(1+W(s)) – передаточная функция замкнутой системы, Ф_ε(s) = 1/(1+W(s)) – передаточная функция замкнутой системы по ошибке, G(s) – изображение Лапласа входного воздействия, следует использовать формулу …

!Task 2Значение ошибки устойчивой системы с астатизмом первого порядка при постоянном значении входного воздействия стремится к …

!Task 3Значение ошибки устойчивой системы с астатизмом первого порядка при линейно возрастающем входном воздействии стремится к …

Правильный ответ:
к постоянной величине.

!Task 4 Значение ошибки устойчивой системы с астатизмом первого порядка при входном воздействии g(t) = G₀*t 2 стремится к …

!Task 5В системе с единичной обратной связью и передаточной функцией разомкнутого контура W(s) амплитуда ошибки Х при гармоническом входном воздействии амплитудой G и частотой ω_к может быть вычислена по формуле …

!Task 6Повысить точность системы можно …

Правильный ответ:
используя изодромное звено

!Task 7Повысить точность системы можно …

Правильный ответ:
используя комбинированное управление.

!Task 8Использование интегрирующего звена для повышения порядка астатизма приводит к изменению запаса устойчивости по фазе на …

!Task 9Статическая система отрабатывает с постоянной установившейся ошибкой _____________ входное воздействие.

Правильный ответ:
постоянное входное воздействие.

!Task 10Система с астатизмом первого порядка отрабатывает с нулевой установившейся ошибкой _____________ входное воздействие.

Правильный ответ:
постоянное входное воздействие.

!Task 11Система с астатизмом первого порядка отрабатывает с постоянной установившейся ошибкой _____________ входное воздействие.

Правильный ответ:
линейно изменяющееся входное воздействие.

!Task 12Ошибка в системе с астатизмом первого порядка стремится к ¥ при _____________ входном воздействии.

Правильный ответ:
входном воздействии с постоянным ускорением.

!Task 13Ошибка в устойчивой статической системе стремится к ¥ при __________ входном воздействии

Правильный ответ:
линейно возрастающем входном воздействии.

!Task 14Низкочастотная часть логарифмической амплитудной характеристики определяет величину …

Правильный ответ:
постоянной времени.

!Task 15Интегральный закон управления применяется для повышения …

Правильный ответ:
точности работы системы.

!Task 16Пропорционально-интегральный регулятор описывается передаточной функцией вида ( К_i – постоянные числа ) …

3. Дидактическая единица ГОС: Анализ качества систем управления

4. Тема задания: Анализ качества переходных процессов

!Task 1После подачи на вход системы единичного воздействия был зафиксирован максимум выходной величины, равный 1.17; установившееся значение выходной величины составило 0.9. Значение перерегулирования равно ___ %.

!Task 2 При снятии переходной характеристики системы было зафиксировано значение перерегулирования, равное 50%. После уменьшения значения общего коэффициента передачи разомкнутого контура, значение перерегулирования снизилось до 30%. Запас устойчивости системы …

Правильный ответ:
увеличился.

!Task 3 При снятии переходной характеристики системы было зафиксировано значение перерегулирования, равное 30%. После увеличение значения общего коэффициента передачи разомкнутого контура, значение перерегулирования снизилось до 50%. Запас устойчивости системы …

Правильный ответ:
уменьшился.

!Task 4Корни характеристического уравнения замкнутой системы равны:λ_1,2 = -0.6 ±j0.3, λ₃ = -0.9, где j – мнимая единица. Степень устойчивости системы равна …

!Task 5 Корни характеристического уравнения замкнутой системы равны:λ_1,2 = -0.9 ±j0.3, λ_3,4 = -1.8 ±j0.6, где j – мнимая единица. Степень устойчивости системы равна …

!Task 6 Корни характеристического уравнения замкнутой системы равны:λ₁ = -10 , λ₂ = -21, λ₃ = -23 , λ₄ = -46. Степень устойчивости системы равна …

!Task 7 Корни характеристического уравнения замкнутой системы равны:λ₁ = -1+j , λ₂ = -1-j, λ₃ = -10. Степень устойчивости системы равна …

!Task 8 Корни характеристического уравнения замкнутой системы равны:λ₁ = j , λ₂ = -j. Степень устойчивости системы равна …

!Task 9После подачи на вход системы единичного воздействия был зафиксирован максимум выходной величины, равный 1.0; установившееся значение выходной величины составило 0.8. Значение перерегулирования системы равно ___ %.

!Task 10После подачи на вход системы единичного воздействия был зафиксирован максимум выходной величины, равный 1.5; установившееся значение выходной величины составило 1.0. Значение перерегулирования системы равно ___ %.

3. Дидактическая единица ГОС: Показатели качества переходных процессов

4. Тема задания: Показатели качества переходных процессов

!Task 1Величина перерегулирования σ% вычисляется по переходной функции h(t) устойчивой системы ( при известных h_max – максимальное значение, h(¥) – установившееся значение, h(0) – начальное значение) по формуле …

!Task 2Значение перерегулирования характеризует …

Правильный ответ:
запас устойчивости системы.

!Task 3Длительностью переходного процесса называется …

Правильный ответ:
интервал времени от момента приложения на вход системы единичного скачка до момента, после которого отклонение выходной величины от установившегося значения по модулю не превосходит допустимую ошибку.

!Task 4Длительность переходного процесса характеризует …

Правильный ответ:
быстродействие системы.

Передаточная функция замкнутой системы по задающему воздействию соответствует апериодическому звену второго порядка с коэффициентом передачи 0,98. Значение перерегулирования у такой системы равно …

Правильный ответ:
равно 0.

!Task 6Степенью устойчивости системы называется

Правильный ответ:
абсолютное значение вещественной части ближайшего к мнимой оси в левой полуплоскости корня характеристического уравнения системы.

!Task 7Динамические показатели качества системы служат для анализа …

Правильный ответ:
качества переходного режима работы системы.

!Task 8Перерегулирование характеризует …

Правильный ответ:
качество переходных процессов системы.

!Task 9Время переходного процесса характеризует …

Правильный ответ:
быстродействие системы.

!Task 10Частота среза желаемой логарифмической амплитудной характеристики определяется по заданному значению

Правильный ответ:
времени переходного процесса.

!Task 11Протяженность среднечастотной части желаемой логарифмической амплитудной характеристики определяется допустимой величиной …

Правильный ответ:
перерегулирования.

!Task 12Заданный показатель колебательности системы определяет …

Правильный ответ:
протяженность участка с наклоном -20 дб/декаду среднечастотной части ЛАХ.

!Task 13Среднечастотная часть логарифмической амплитудной характеристики определяется на оси частот значением …

Правильный ответ:
частоты среза.

!Task 14Среднечастотная часть логарифмической амплитудной характеристики определяет …

Правильный ответ:
время переходного процесса и перерегулирование.

!Task 15Запас по фазе для замкнутой системы определяется по фазовой характеристике разомкнутого контура на частоте …

Правильный ответ:
среза системы

3. Дидактическая единица ГОС: Устойчивость непрерывных систем управления

4. Тема задания: Частотные методы исследования устойчивости линейных систем

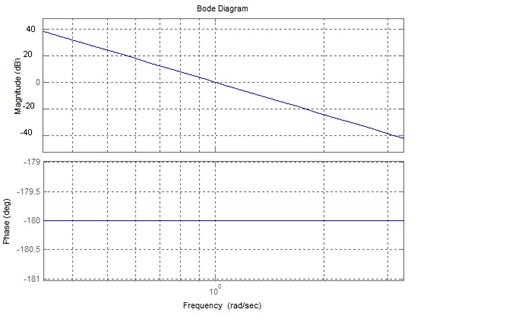
!Task 1Запас устойчивости по фазе системы определяется по логарифической амплитудно-фазо-частотной характеристике как … Правильный ответ:180°+ аргумент (фаза) частотной передаточной функции на частоте среза

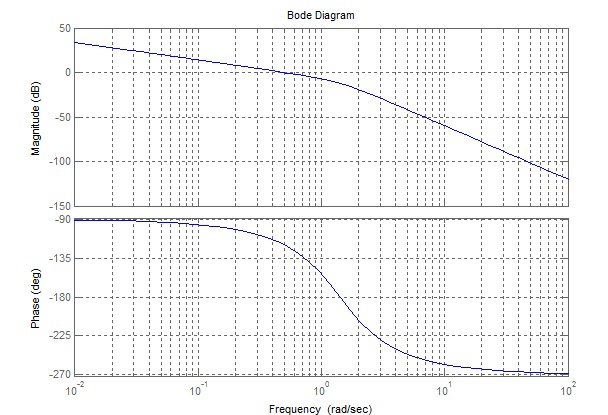
Логарифическая амплитудно-фазо-частотная характеристика системы приведена на рисунке.

Запас устойчивости по фазе данной системы равен …

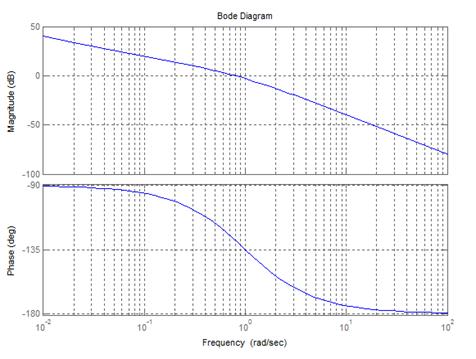
Логарифическая амплитудно-фазо-частотная характеристика системы приведена на рисунке.

Запас устойчивости по фазе данной системы …

Правильный ответ:
отсутствует, система неустойчива.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Запас устойчивости по амплитуде замкнутой системы …

Правильный ответ:
бесконечен.

!Task 5Для устойчивости замкнутой системы, необходимо, чтобы амплитудно-фазовая характеристика разомкнутой системы …Правильный ответ:
не охватывала точку (-1;j0). !Task 6На рисунке представлен годограф разомкнутой системы. Замкнутая система … 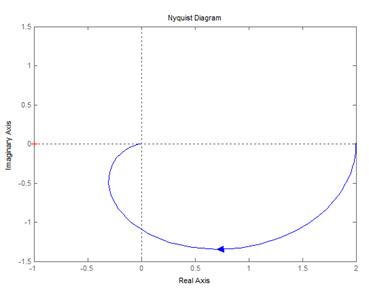Правильный ответ:
является устойчивой. !Task 7На рисунке представлен годограф разомкнутой системы. Замкнутая система … 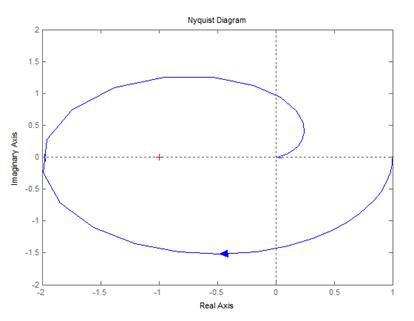Правильный ответ:
является неустойчивой. !Task 8На рисунке представлен годограф разомкнутой системы. Замкнутая система … 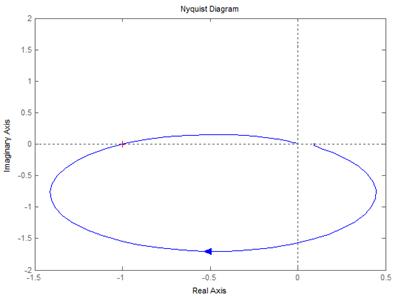Правильный ответ:
находится на границе устойчивости. !Task 9 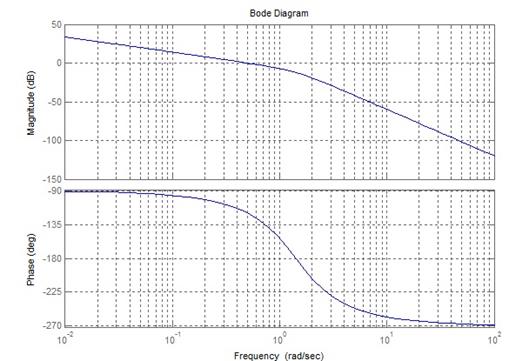Для того, чтобы повысить запас устойчивости системы по фазе необходимо Правильный ответ:
уменьшить коэффициент усиления разомкнутого контура. !Task 10На рисунке представлен годограф разомкнутой системы. Для того, чтобы замкнутая система была устойчивой необходимо … 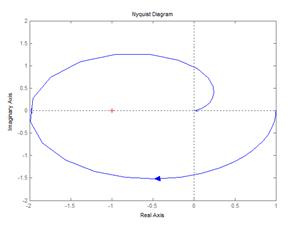Правильный ответ:
уменьшить коэффициент усиления разомкнутого контура.

Логарифическая амплитудно-фазо-частотная характеристика системы приведена на рисунке.

Запас устойчивости по фазе данной системы …

Правильный ответ:
отсутствует, система на границе устойчивости.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Запас устойчивости по амплитуде замкнутой системы …

Правильный ответ:
отсутствует, система на границе устойчивости.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Замкнутая система неустойчива. Для того, что замкнутая система стала устойчивой, необходимо …

Правильный ответ:
уменьшить коэффициент усиления системы.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Замкнутая система неустойчива. Для того, что замкнутая система стала устойчивой, необходимо …

Правильный ответ:
уменьшить коэффициент усиления системы.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Данная система …

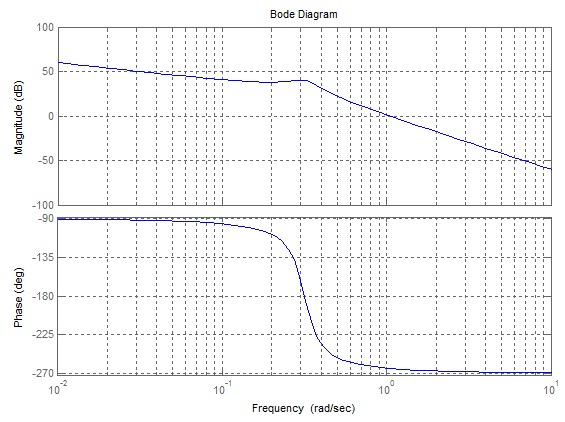
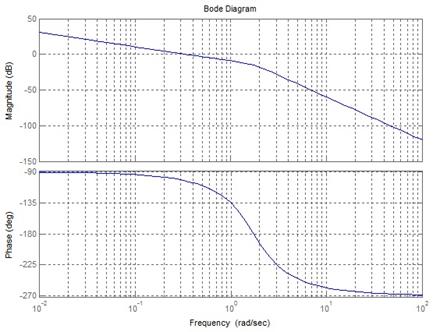
Правильный ответ:
является устойчивой

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Данная система …

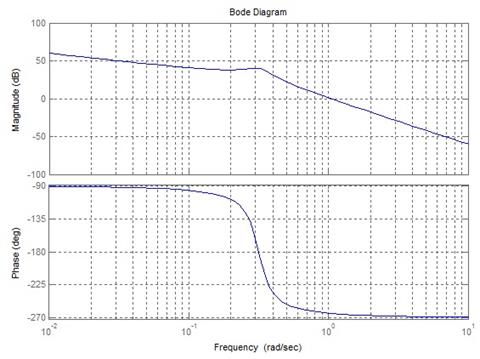
Правильный ответ:
является неустойчивой.

Логарифическая амплитудно-фазо-частотная характеристика разомкнутой системы приведена на рисунке.

Данная система … Правильный ответ:
находится на границе устойчивости. !Task 18На рисунке представлен годограф разомкнутой системы. Замкнутая система … 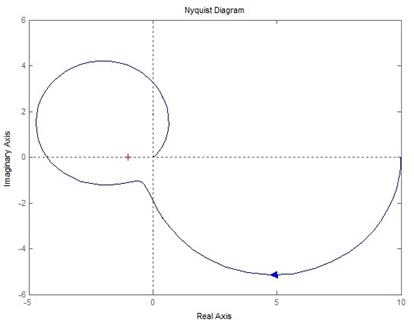Правильный ответ:
является неустойчивой. !Task 19На рисунке представлен годограф разомкнутой системы. Замкнутая система … 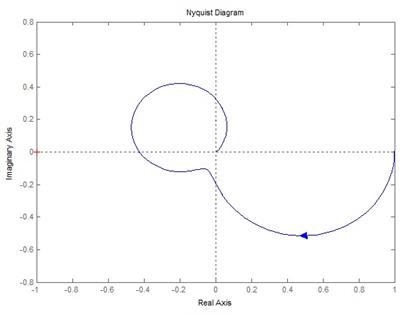Правильный ответ:
является устойчивой. !Task 20На рисунке представлен годограф разомкнутой системы. Для того, чтобы замкнутая система была устойчивой необходимо … 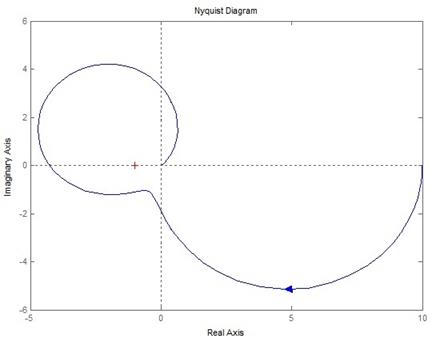Правильный ответ:
уменьшить коэффициент усиления разомкнутого контура.
!Task 21На рисунке представлен годограф разомкнутой системы. Замкнутая система … 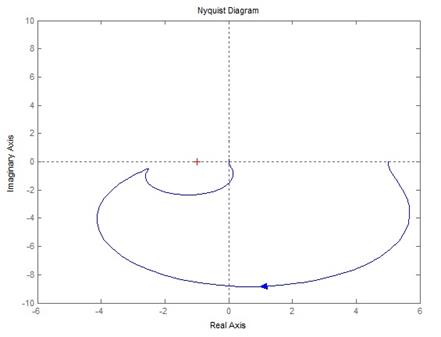Правильный ответ:
является устойчивой.

3. Дидактическая единица ГОС: Устойчивость непрерывных систем управления

4. Тема задания: Области и запасы устойчивости

Система, заданная передаточной функцией в разомкнутом состоянии вида: 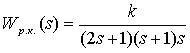в замкнутом состоянии будет находиться на границе устойчивостипри значении k равном … Правильный ответ:1.5

Разомкнутая система с передаточной функцией разомкнутого контура 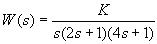будет устойчива при значении К … Правильный ответ:

📽️ Видео