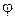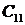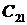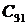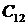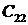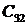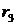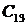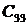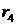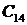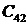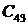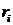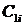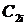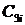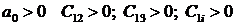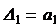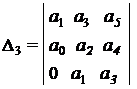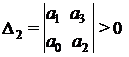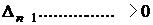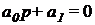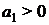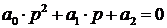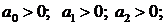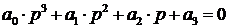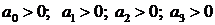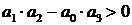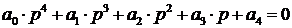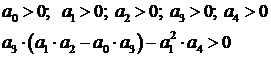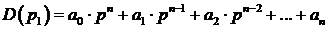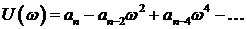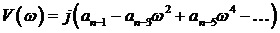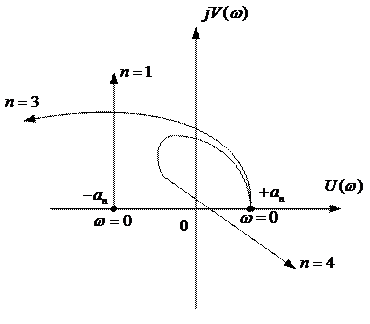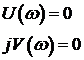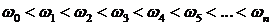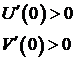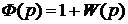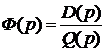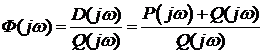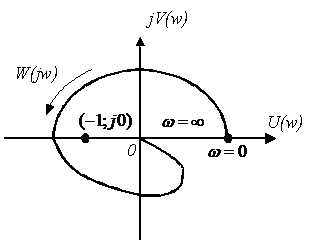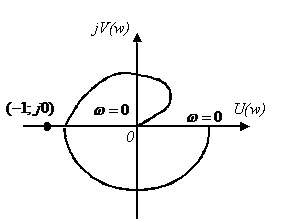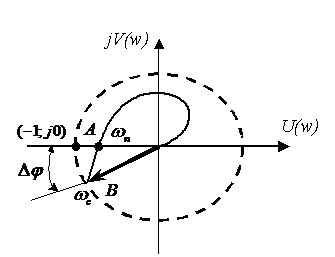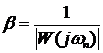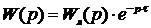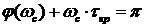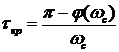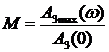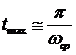Одним из косвенных показателей качества систем управления является степень удаленности корней характеристического уравнения замкнутой САУ от мнимой оси комплексной плоскости. Пусть ближайшие к мнимой оси комплексно-сопряженные корни устойчивой системы имеют значение
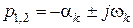
Расстояние 
Угол φ, образуемый лучами, проведенными из начала координат через эти корни, характеризует колебательность системы. Степенью колебательности системы (коэффициентом затухания колебаний) называют количественную характеристику, определяемую выражением

Чтобы система обладала заданной колебательностью, все корни характеристического уравнения должны вписываться в угол 2φ (см. рис. 7.2). Для большинства систем управления допустимое перерегулирование 
Рис. 7.2. Область расположения корней
с заданными показателями 
При корневых методах оценки качества системы, т. е. по расположению корней характеристического полинома, исходят из следующих соображений.
Решение однородного уравнения, характеризующего свободное движение системы, представляет собой сумму затухающих экспонент вида (6.2). Полагая, что качество САУ в основном определяется ближайшим к мнимой оси вещественным корнем или ближайшей к мнимой оси парой комплексно-сопряженных корней (доминирующих корней), можно записать
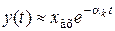
Полагая, что зона δ установления переходного процесса составляет (2…5)% от установившегося значения 


Следовательно, задаваясь временем регулирования, можно рассчитать минимальное (по модулю) значение вещественных частей корней характеристического уравнения.
Аналогично можно связать степень колебательности m системы со степенью затухания колебаний. Пусть по условиям технологии требуется, чтобы каждая последующая амплитуда колебаний затухала в k раз по сравнению с предыдущей. Тогда
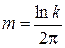
Пусть k=10, тогда в соответствие с (7.4) получим m=0,336 и
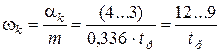
Таким образом, задаваясь временем регулирования 

Для построения в плоскости параметров областей, обеспечивающих требуемые показатели качества регулирования целесообразно использовать метод D-разбиения [6]. В качестве примера используем уравнение Вышнеградского, описывающего в параметрической форме характеристический полином 3-го порядка,

где A и B – обобщенные параметры характеристического уравнения.
Подставим выражение для комплексного корня 

Приравнивая нулю вещественную и мнимую части, получим


Полагая 


Рис. 7.3. Границы областей устойчивости,
колебательности и апериодичности на
Полагая 

Поскольку на кривой 1 ω ≠ 0, а на кривых 2 и 3 ω = 0, то области I и III являются областями комплексных, а область II – вещественных корней (см. рис. 7.3). Следовательно, если параметры A, B принадлежат области II, то переходные процессы имеют апериодический характер, причем, чем эти параметры больше, тем процессы более затянуты. Если параметры принадлежат области I, то переходные процессы имеют колебательный характер, причем, чем больше A и меньше B, тем выше колебательность. Область III является областью монотонности решения однородного дифференциального уравнения, соответствующего (7.5), а, следовательно, переходные процессы, имея колебательный характер, тем не менее, затухают монотонно (без перерегулирования).
Диаграмма Вышнеградского [19] помимо приведенных кривых содержит кривые равных вещественных частей комплексных корней (равной степени устойчивости), причем для двух случаев расположения корней, когда ближайшими к мнимой оси являются комплексные корни и, когда ближайшим к мнимой оси расположен вещественный корень (на рис. 7.3 эти кривые не показаны). В частности, на границе областей I и III (кривая 4) все три корня равно удалены от мнимой оси.
Требования повысить быстродействие и одновременно снизить перерегулирование в системе являются противоречивыми друг другу, что заставляет искать компромисс. В общем случае, с точки зрения переходного процесса наилучшей считается САУ, у которой все корни характеристического уравнения n-го порядка равны друг другу (на практике редко реализуется), т. е.
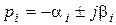
В этом случае перерегулирование не превышает 10%, а время нарастания регулирования является минимальным.
Если все корни являются вещественными, то система характеризуется отсутствием перерегулирования, т. е. апериодическими переходными процессами. Время регулирования будет тем меньше, чем меньше среднегеометрический корень 
При анализе качества системы корневыми методами необходимо учитывать влияние нулей передаточной функции на переходный процесс.
Прежде всего, нужно проверить, насколько близки нули к полюсам.
Если нуль и полюс совпадают, то их нужно сократить, и они не будут влиять на качество системы. Порядок системы при этом, естественно, будет понижен.
Если полюсы и нули передаточной функции не совпадают, то полюсы определяют отдельные составляющие переходного процесса (апериодические и гармонические), а нули определяют удельный вес каждой из этих составляющих. Чем ближе нуль передаточной функции расположен к какому-либо полюсу, тем меньше его вклад в переходную характеристику составляющей, соответствующей данному полюсу.
7.2.2. Интегральные оценки качества
В основе интегральных оценок качества лежит предположение, что качество регулирования тем выше, чем меньше площадь между кривой переходного процесса и заданным значением регулируемой переменной. Интегральные оценки качества являются строгой математической формулировкой понятия качества системы, и их минимизация позволяет определить оптимальные параметры системы управления, т. е. решить задачу параметрического синтеза системы. Для этой цели применяются процедуры безусловной и условной оптимизации [2, 6, 10-12, 19-21].
Наибольшее применение для косвенной оценки качества САУ находят интегральные оценки вида [6, 11, 12, 19]:





где 
С – некоторый весовой коэффициент, характеризующий допустимую скорость изменения ошибки регулирования, а, следовательно, выходной координаты в переходном процессе.
В критерии (7.8) подынтегральное выражение линейно относительно ошибки регулирования и такая оценка применяется только для апериодического переходного процесса, когда ошибка имеет положительный знак.
Интегральная квадратичная оценка (ИКО) вида (7.9) применяется при колебательном характере переходных процессов, характеризующихся сменой знака ошибки регулирования. Интегральная квадратичная оценка (7.10) применяется в тех случаях, когда требуется учитывать ограничения энергии управления.
Широко используемым видом оценки качества является интеграл от модуля ошибки (ИМО) – (7.11), позволяющем учесть смену знака подынтегральной функции.
Чтобы уменьшить вклад начальной ошибки в интеграл (7.11) и учесть связанную с этим ошибку была предложена [6] оценка в виде интеграла от взвешенного модуля ошибки (ИВМО) в виде (7.12).
Рассмотрим пример. Пусть передаточная функция замкнутой системы 2-го порядка имеет вид:

где 
Нормированное значение собственной частоты принято 

Рис. 7.4. Интегральные оценки
качества системы второго порядка
Как видим, оценка ИВМО по сравнению с ИКО имеет ярко выраженный минимум (хорошую избирательность), соответствующий 
Рассмотрим еще один пример. Пусть передаточная функция замкнутой системы имеет достаточно общий вид нерекурсивного фильтра n-го порядка:

Безусловная оптимизация систем первого-четвертого порядка (n=1…4), описываемых передаточными функциями (7.14), по критерию ИВМО дает оптимальные значения коэффициентов полиномов знаменателей этих передаточных функций, приведенные в табл. 7.1. Значения коэффициентов нормированы относительно собственной частоты колебаний 
На рис. 7.5 приведены кривые переходных процессов, соответствующих оптимальным по критерию ИВМО фильтрам первого-четвертого порядка.
| Порядок системы | Полином знаменателя передаточной функции |
| n=1 |  |
| n=2 |  |
| n=3 |  |
| n=4 |  |
Значения коэффициентов нормированы относительно собственной частоты колебаний 
Рис. 7.5. Переходные характеристики, соответствующие
оптимизации систем по ИВМО
Графики построены в зависимости от нормированного времени 
Кроме приведенных оценок для оптимизации систем управления применяются и другие интегральные критерии качества, в частности, лежащие в основе синтеза фильтров Баттерворта, широко применяемых при настройке контуров электромеханических систем управления.
8. Метод пространства состояний
Широкое распространение компьютеров и мощных систем программирования побуждает к исследованию САУ во временной области, а, следовательно, к непосредственному использованию описания динамических систем управления в форме обыкновенных дифференциальных уравнений без перехода к операторной форме. Кроме того, как уже отмечалось, векторно-матричные формы описания и исследования применимы не только к одномерным, линейным, стационарным САУ, но и к широкому классу многомерных, нелинейных и нестационарных САУ.
Чтобы получить пригодную для компьютерного синтеза и анализа модель САУ, необходимо представить ее в переменных состояния системы, используя далеко не единственный набор переменных. Следует отметить, что описание систем во временной области в векторно-матричной форме лежит в основе современной теории управления и оптимизации. В настоящей главе рассмотрены вопросы применения метода пространства состояния к непрерывным системам управления.
8.1. Векторно-матричное описание САУ
Состояние системы – это совокупность значений переменных системы (координат состояния), существенных с точки зрения решаемой задачи. В общем случае, в это число включают не только выходные и внутренние переменные САУ, но и задающие воздействия, и доминирующие возмущающие воздействия внешней среды. Чем полнее достоверной информации о состоянии системы в текущий момент времени, тем проще определить будущие значения всех ее переменных. Инженерно-технический персонал, разрабатывающий и эксплуатирующий технические системы управления, оперирует, как правило, с такими физическими переменными, которые могут быть измерены с помощью соответствующих датчиков. К таким физическим переменным САУ относят ускорение, скорость, перемещение, давление, расход, температуру, уровень и т. п. Координатами датчиков технологических координат САУ являются другие переменные — напряжение, ток, частота следования импульсов, двоичный код и т. п., что дает исследователю возможность выбора для синтеза и анализа необходимого набора координат состояния САУ.
Векторно-матричная модель многомерной, нелинейной, нестационарной САУ записывается в виде [6, 10, 11, 19]


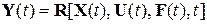
где X(t), U(t),F(t), Y(t) – соответственно векторы состояния, управления, возмущения и выходных (управляемых) координат системы,


В уравнении (8.1) вектор управления U(t) является, в общем случае, некоторой нелинейной нестационарной функцией задающих координат, координат состояния и возмущения САУ и призван обеспечить оптимальное управление системой. Описание многомерных, нелинейных, нестационарных САУ в форме (8.1) не позволяет, как правило, получить инженерное решение задачи структурно-параметрического синтеза оптимального управления U(t) или такое решение приводит к неоправданным затратам на реализацию (в техническом или экономическом аспектах). В большинстве случаев такие модели сводят к одномерным или многомерным линейным (линеаризованным) квазистационарным моделям, для которых имеются развитые методы и инженерные методики синтеза оптимального управления.
Линейную (линеаризованную) модель многомерной стационарной (квазистационарной) САУ представляют в виде системы обыкновенных дифференциальных уравнений первого порядка в форме Коши:



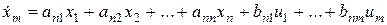
Эту же систему дифференциальных уравнений можно представить в векторно-матричной форме [6, 11, 19]:

где 



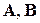


В общем случае, на объект управления помимо управляющих воздействий действуют возмущающие воздействия. В этом случае векторно-матричную модель системы представляют в виде

где 


Выходные (управляемые) переменные не всегда непосредственно принадлежат вектору состояния. В линейных САУ они линейно связаны с переменными состояния, управляющими и возмущающими переменными. В этом случае к уравнениям (8.3), (8.4) присоединяют алгебраические линейные уравнения

или 
где 
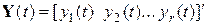
K, L, M – стационарные матрицы соответственно размерностей (r 


Следует отметить, что приведенные уравнения (8.1)…(8.6) дают описание лишь объекта управления или разомкнутой системы, если вектор управления U(t) не является функцией координат состояния САУ. В замкнутых линейных САУ управление обычно формируют как линейную форму координат состояния и, в общем случае, возмущения САУ.
В качестве примера приведем векторно-матричное описание ранее рассматриваемого электродвигателя постоянного тока как объекта регулирования по цепи якоря. Пусть выходной (регулируемой) координатой является скорость вращения двигателя. Полагая, что напряжение возбуждения 
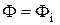



Воспользуемся векторно-матричной моделью линейных САУ в виде (8.4), (8.5). Зададимся векторами состояния, управления и возмущения в виде:

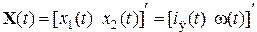


По уравнениям (8.7) найдем матрицы состояния, управления и возмущения:
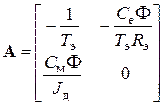


Поскольку выходная переменная всего одна и ей является координата состояния 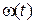
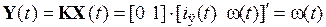
По описанию системы в форме векторно-матричных уравнений (ВМУ) можно непосредственно получить эквивалентную передаточную функцию (ПФ) и, наоборот, зная ВМУ системы, можно получить ее ПФ. Для этого в системе MATLAB имеется две функции: функция tf и функция ss.
Пусть ВМУ системы имеет вид (8.3), (8.5). Применительно к системе MATLAB ВМУ записывают в виде

Для получения ВМУ в системе MATLAB необходимо определить функцию ss(A,B,C,D). Для преобразования ВМУ к ПФ системы необходимо записать:
sys_ss=ss(A,B,C,D); % Формирование ВМУ системы;
sys_tf=tf(sys_ss), % Преобразование ВМУ к ПФ системы.
Для обратного преобразования ПФ к ВМУ необходимо записать:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); Преобразование ПФ к ВМУ системы.
Рассмотрим пример. Пусть ПФ системы имеет вид
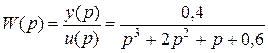
Тогда запишем скрипт преобразования ПФ к ВМУ и обратного преобразования ВМУ к ПФ:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); %Преобразование ПФ к ВМУ системы;
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Корни характеристического уравнения замкнутой системы
Характер свободного движения всей системы при наличии различных корней определяется суммой свободных составляющих формулы (3.3.), причем система бывает устойчивой, если все вещественные корни отрицательные и комплексные корни имеют отрицательную вещественную часть. Если корни нанести на плоскость комплексного переменного, то можно выделить устойчивые, неустойчивые и нейтральные зоны.




Линейная САУ устойчива, если корни характеристического уравнения расположены слева от мнимой оси. Система считается нейтральной, если корни принадлежат мнимой оси.
Неустойчивой система считается для случая, когда корни лежат справа от мнимой оси.
Вышеперечисленные условия устойчивости используются для формулирования необходимого условия устойчивости линейных САУ.
Кроме выше записанного необходимое условие устойчивости можно записать, используя известное в математике выражение:
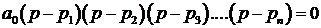
Подставив в выражение (3.6.) только устойчивые корни характеристического уравнения можно заметить, что после раскрытия скобок в уравнении (3.6.) устойчивой системы все коэффициенты характеристического уравнения будут положительными.
Необходимое условие устойчивости – положительность всех коэффициентов характеристического уравнения. В том случае, если один из коэффициентов отрицателен – линейную систему нельзя считать устойчивой.
Для уравнений первого и второго порядка условие положительности коэффициентов характеристического уравнения является кроме необходимого еще и достаточное условие. Это можно охарактеризовать тем, что уравнения первого и второго порядка просты для нахождения корней. Начиная с третьего и выше порядков характеристические уравнения трудно разрешить в нахождении корней простыми способами вычисления. Поэтому в теории автоматического управления разработаны упрощенные правила – критерии нахождения устойчивости линейных систем.
Существует два вида критериев: алгебраические и частотные. С математической точки зрения все рассматриваемые критерии равнозначны.
§ 3.2.3 Алгебраический критерий устойчивости. Критерий Рауса
Данный критерий устойчивости был разработан в 1878 г . английским математиком Раусом и который был сформулирован в виде некого правила или алгоритма, который можно представить в виде таблицы (матрицы).
Таблица Рауса составляется на основании характеристического уравнения линейной системы вида:
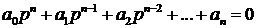
Покажем эту таблицу:
Порядок заполнения таблицы Рауса:
1) в первой строке таблицы Рауса в порядке увеличения индексов записываются коэффициенты характеристического уравнения (3.7), имеющие четный индекс: 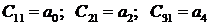
2) во второй строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения (3.7.) с нечетными индексами: 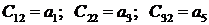
Любой из остальных коэффициентов таблицы Рауса записывается в соответствии со следующими выражениями:
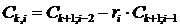
к – столбец, i – строка
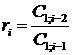
Число строк таблицы Рауса равно степени характеристического уравнения + 1 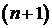
Условие устойчивости Рауса: для того, чтобы линейная САУ была устойчивой необходимо и достаточно чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при 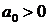
§ 3.2.4 Алгебраический критерий устойчивости. Критерий Гурвица
В 1895 г . немецкий математик Гурвиц разработал алгебраический критерий устойчивости в форме определителей, состоящих из коэффициентов характеристического уравнения (3.7).
В основе рассматриваемого критерия лежит построение главного определителя Гурвица из коэффициентов характеристического уравнения (3.7).
Порядок составления главного определителя Гурвица:
1. Записываем главную диагональ определителя Гурвица, составленную из коэффициентов характеристического уравнения от 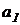
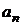
2. Вверх от главной диагонали записывают столбцы, составленные из коэффициентов характеристического уравнения с последовательно возрастающими индексами;
3. Вниз от главной диагонали записываем столбцы составленные из коэффициентов характеристического уравнения с последовательно убывающими индексами;
4. Оставшиеся пустые места определителя заполняются нулями, т.е. нули проставляются на места, где должны быть коэффициенты с индексами больше 0 и меньше 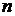
Главный определитель Гурвица имеет вид:
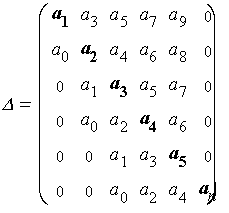 |
После построения главного определителя Гурвица, в нем очеркиваются диагональные миноры и тем самым получаются определители более низших порядков.

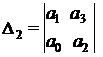
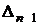
Критерий устойчивости Гурвица: для того, чтобы система автоматического управления (САУ) была устойчивой необходимо и достаточно, чтобы все определители Гурвица (3.11) имели знаки одинаковые со знаком первого коэффициента характеристического уравнения 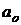
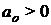
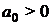
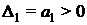
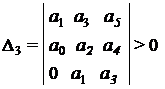
В случае, если хоть одно из условий не выполняется, то систему считают неустойчивой.
Раскрывая все определители Гурвица можно для уравнений 1-го, 2-го, 3-го и 4-го порядков записать более простую форму критерия устойчивости. Такая форма записи получила название следствия из критерия Гурвица или ее называют критерием Леера-Шепорда.
1) Для характеристического уравнения 1-го порядка:
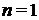
необходимым и достаточным является, чтобы:
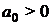
2) Для характеристического уравнения 2-го порядка:
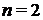
необходимым и достаточным является, чтобы:
3) Для характеристического уравнения 3-го порядка:
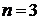
необходимым и достаточным является, чтобы:
4) Для характеристического уравнения 4-го порядка:
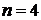
необходимым и достаточным является, чтобы:
§ 3.2.5 Частотный критерий устойчивости. Критерий Михайлова
Все частотные критерии, в том числе и критерий Михайлова, основаны на хорошо известном из курса высшей математики «Принципа аргумента», который позволяет отобразить необходимое условие устойчивости на частотной плоскости.
Все элементарные вектора 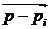

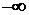
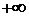
Этот частотный критерий устойчивости был сформулирован в 1938 г . советским ученым Михайловым и является интерпретацией принципа аргумента, позволяя судить об устойчивости системы наблюдая за поведением кривой называемой кривой Михайлова.
За основание построения кривой берется характеристический полином вида:
Произведя замену 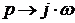
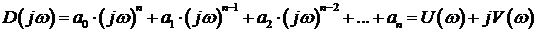
При изменении частоты 
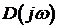
Для устойчивых систем кривая Михайлова начинаясь при 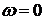

Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы кривая или годограф Михайлова при изменении 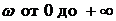
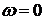
Нейтральные САУ (граница устойчивости):
Анализируя кривую Михайлова можно вывести следствие из него: при прохождении кривой Михайлова числа квадрантов комплексной плоскости, происходит последовательное поочередное пересечение действительной и мнимой соей, т.е.:
Значение частот при которых происходит пересечение кривой с вещественной или мнимой осью, должны является корнями уравнений (3.20) и (3.21), причем 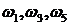
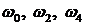
В связи с выше записанным следствие кривой Михайлова можно сформулировать следующим образом: САУ будет устойчивой тогда и только тогда, когда вещественная 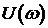
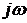
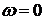
Для реализации этого следствия определяются только корни уравнения 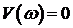
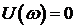
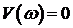
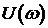
§ 3.2.6 Частотный критерий. Критерий Найквиста
Этот критерий разработан в 1923 г . американским ученым Найквистом. Он позволяет судить об устойчивости замкнутой системы по поведению АФЧХ разомкнутой системы.
Вектор 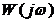

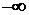
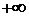
Кривая, описываемая окончанием этого вектора есть АФЧХ разомкнутой системы, причем следует отметить, что вид этой характеристики симметричен относительно начала координат, т.е.
Для доказательства критерия Найквиста используют дополнительную функцию вида:
Причем в знаменателе такой функции будет записан характеристический полином разомкнутой системы, а в числителе характеристический полином замкнутой системы:
В случае замены оператора Лапласа р на 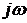
Пусть характеристическое уравнение замкнутой системы 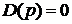
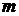
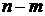
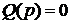
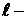
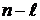
При рассмотрении этого критерия так же работает принцип аргумента, который определяет, что устойчивой система является, когда вектор 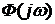
Разомкнутая система являющееся неустойчивой и имеющая 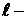
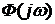

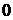
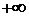
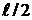
Найквистом было отмечено, что движение вектора 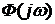
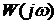
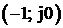
Критерий устойчивости Найквиста: если разомкнутая система автоматического управления неустойчива, то для того чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы АФЧХ разомкнутой системы 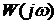

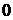
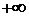
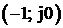
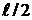
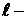
При сложной форме характеристик 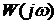
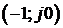
Для анализа поведения таких характеристик применяют «правило переходов» Ципкина. Назовем переход АФЧХ через действительную ось слева от точки 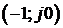

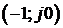
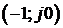
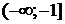
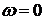
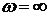
Критерий Найквиста для рассматриваемого варианта: если разомкнутая САУ неустойчива, то для того чтобы замкнутая система стала устойчива необходимо и достаточно, чтобы разность между положительным и отрицательным переходами АФЧХ разомкнутой системы через отрезок вещественной оси 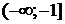

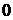
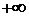
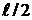
Критерий Найквиста для случая, когда разомкнутая система устойчива имеет следующую формулировку: если САУ разомкнутая устойчива, то замкнутая система будет устойчивой, если АФЧХ разомкнутой системы 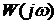
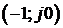
Достоинство критерия Найквиста заключается в том, что его можно использовать даже если неизвестны структуры отдельных звеньев системы, достаточно получить АФЧХ. Кроме того, рассматриваемый критерий позволяет анализировать устойчивость систем обладающих запаздыванием.
§ 3.2.7. Частотный критерий устойчивости – логарифмический частотный критерий
Критерий Найквиста позволяет судить от устойчивости системы по логарифмическим частотным характеристикам, т.е. можно заметить, что критерий Найквиста можно анализировать используя простые с точки зрения построения логарифмические частотные характеристики. Поэтому рассматриваемый критерий часто называют критерием Найквиста в логарифмической форме.
Передаточная функция разомкнутой системы обычно представляет собой произведение элементарных динамических звеньев, асимптотические характеристики которых представляют собой ломаные прямые линии.
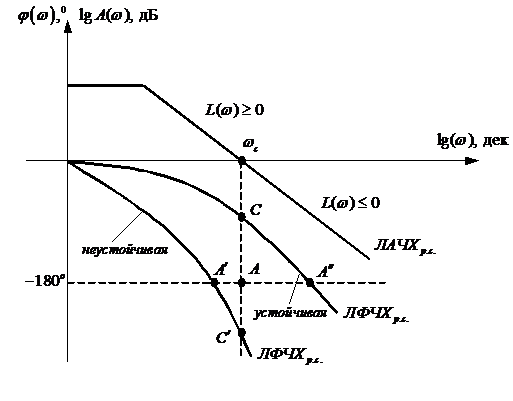
Устойчивость с использованием логарифмического критерия позволяет построив совмещено ЛАЧХ и ЛФЧХ разомкнутой системы судить об устойчивости замкнутой системы.
Замкнутая система автоматического управления устойчива, если при 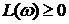
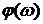
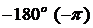
1) система устойчивая в разомкнутом состоянии будет устойчивой и в замкнутом, если точка А ЛФЧХ определяемая фазой 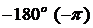
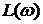
2) САУ неустойчивая в разомкнутом состоянии будет устойчива в замкнутой, если при изменении 
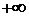
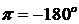
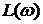
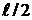
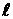
Следствие к первому случаю: САУ будет устойчивая в замкнутом состоянии, если ЛФЧХ неустойчивой разомкнутой системы при 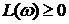
§ 3.2.8. Запасы устойчивости
При проектировании систем автоматики стремятся обеспечить их устойчивость с некоторой гарантией, чтобы изменение параметров системы в процессе ее работы не могли привести к неустойчивости системы. Для реализации такого тезиса необходимо, чтобы система обладала определенным запасом устойчивости. Запас устойчивости определяет удаленность параметров системы от границы устойчивости.
Положение системы на границе устойчивости можно определить, используя критерий устойчивости. Качественную характеристику удаления системы от границы устойчивости дают критерии Гурвица и Михайлова. Четкую количественную характеристику запаса устойчивости как по амплитуде, так и по фазе дает критерий Найквиста и логарифмический критерий.
В соответствии с критерием Найквиста система находится на границе устойчивости, если годограф Найквиста проходит через точку с координатами 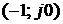
Покажем использование критерия Найквиста для нахождения запаса устойчивости по фазе и амплитуде:
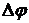
Запас устойчивости по модулю может быть в данном случае рассчитан как:
Значение модуля АФЧХ разомкнутой системы 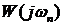
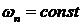
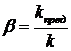
где 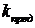
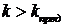
Запас устойчивости по фазе 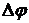
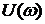
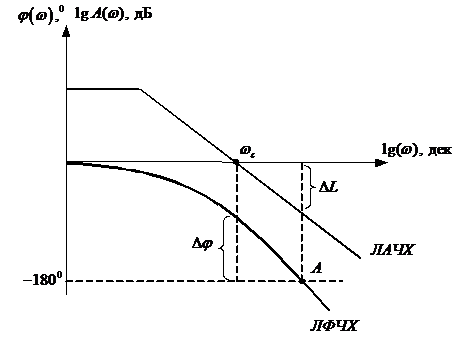
Определение устойчивости по логарифмическим частотным характеристикам может быть осуществлено достаточно простым способом. Необходимо на совмещенных логарифмических частотных характеристиках построить вертикальные проекции между осью абсцисс и значением -180º которые проведены через точки 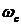
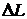
Запасы устойчивости влияют не только на работоспособность (устойчивость) системы, но также характеризуют качество работы системы. В реальных системах обычно 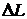
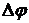
§ 3.2.9. Устойчивость систем обладающих запаздыванием
Значительное число объектов сельскохозяйственного назначения описываются математической моделью, в состав которой входит звено транспортного запаздывания, при этом общая передаточная функция такой системы состоит из произведения передаточной функции линейной части системы и передаточной функции звена транспортного запаздывания
Частотная передаточная функция в данном случае может быть записана в виде:
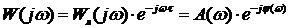
где 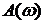
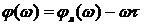
Звено чистого запаздывания не изменяет амплитуду АФЧХ, но создает дополнительный отрицательный сдвиг по фазе, зависящий от частоты 
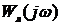
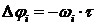
Оценку устойчивости систем с запаздыванием можно также выполнить используя логарифмический частотный критерий.
Очень часто анализируя устойчивость рассмотренных систем необходимо бывает установить значение запаздывания при котором система находится на границе устойчивости. Такое время носит название критического времени запаздывания и оно определяется из следующего выражения:
§ 3.3. Качества работы САУ
§ 3.3.1. Общие положения о качестве работы
Факт устойчивости или неустойчивости САУ говорит лишь о том, что переходная или свободная составляющая процесса регулирования с течением времени расходится или затухает, но такой анализ не дает ответа на такие важные вопросы как: быстрота затухания переходного процесса, форма кривой процесса регулирования и т.д. Поэтому следует отметить, что теория устойчивости является необходимым, но не достаточным условием практической пригодности САУ. Любая такая система кроме устойчивости должна еще обладать и требуемым качеством работы. Качество работы систем автоматики характеризует точность ее работы как в установившемся так и переходном режимах. Иными словами можно отметить, что качество работы системы автоматики характеризует точность воспроизведения системой задающего воздействия.
Проблема качества систем автоматики может быть поставлена как задача анализа, т.е. оценка уже спроектированной САУ или как задача синтеза, т.е. проектирование САУ заранее оговоренными показателями качества. При рассмотрении таких задач будем полагать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами. При изменении воздействия 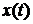
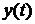
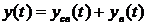
где 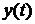
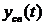
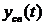
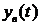
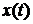
Качество работы системы автоматики можно оценить по виду переходного процесса и по его составляющим 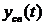
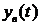
1) показатели качества переходного процесса 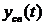
2) показатели качества, характеризующие вынужденную составляющую 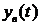
Показатели качества, определяемые непосредственно по кривой переходного процесса называют прямыми оценками качества, косвенные оценки качества не требуют нахождение кривой переходного процесса. Косвенные методы разделяют на: корневые, интегральные и частотные.
§ 3.3.2. Оценка качества регулирования при гармонических воздействиях
При гармонических воздействиях качество системы принято оценивать по амплитудо-фазовой, амплитудо-частотной и логарифмическим частотным характеристикам.
Для оценки качества переходных процессов системы можно использовать следующие величины: показатель колебательности М, резонансная (собственная частота) 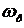
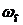
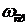
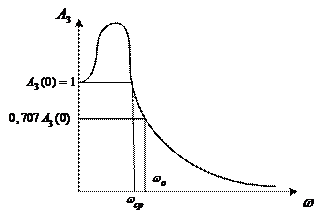
Показатель колебательности М – это отношение максимального значения АЧХ 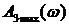
при 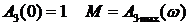
Показатель колебательности характеризует склонность системы к колебаниям. Чем выше М, тем менее качественная система при прочих равных условиях.
Частоту 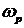
Полоса пропускания системы – это интервал частот от 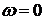
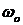
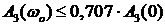
или при 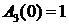
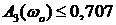
Частота среза 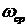
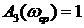
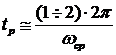
если переходный процесс имеет одно-два колебания, то время достижения переходной характеристикой первого максимума
Склонность системы к колебаниям характеризуется величинами ее запасов устойчивости по модулю и по фазе. Запасы устойчивости рассчитывают по АФЧХ и ЛЧХ. В хорошо демпфированных системах запас устойчивости по амплитуде колеблется в пределах от 6 до 20 дБ, а запас по фазе – от 30 до 60º.
Т.к. рассмотренные выше показатели косвенно определяют быстродействие, перерегулирование и т.п., то они могут быть использованы и для расчета систем, находящихся под воздействием непериодических возмущений.
Видео:Характеристическое уравнение в ДУСкачать

Типовые передаточные функции и характеристическое уравнение
Для описания системы вводят передаточные функции, связывающие определенные входы и выходы.
1. Передаточная функция разомкнутой системы определяется как произведение всех передаточных функций по основному контуру. Она единственная и не зависит от точки размыкания:
2. Передаточная функция замкнутой системы по задающему воздействию определяется как отношение изображения выходной координаты (в данном случае – скорости вращения двигателя) к изображению задающего воздействия:
3. Передаточная функция замкнутой системы по возмущающему воздействию определяется как отношение изображения выходной координаты к изображению возмущающего воздействия (в данном случае – момента нагрузки):
Стандартная схема системы
В целях унификации вводится стандартная структурная схема системы с единичной обратной связью, стандартными обозначениями входов и выходов и типовых передаточных функций.
| Y(s) |
| F(s) |
| f |
| v |
| V(s) |
| y |
| W(s) |
| ε |
| E(s) |
Рисунок 7.2. стандартная схема системы
1. Передаточная функция разомкнутой системы:



2. Передаточная функция по задающему воздействию:
Приравниваем знаменатель к нулю, получаем характеристическое уравнение замкнутой системы.

3. Передаточная функция по возмущению:
4. Передаточная функция по ошибке:
Понятие устойчивости
Очень важно изучить поведение системы во времени. В некоторых случаях процессы оказываются расходящимися, что свидетельствует о неустойчивости системы.
Для нормальной эксплуатации система должна быть устойчивой, т.е. после действия возмущения она должна возвращаться в состояние равновесия.
В качестве примера рассмотрим поведение шарика на вогнутой поверхности (желоб), выпуклой поверхности и плоской поверхности.
Устойчивая система (вогнутая поверхность), процесс сходится:
| X |
| x0 |
| t |
Неустойчивая система (выпуклая поверхность), процесс расходится:
| t |
| X |
| x0 |
Нейтральная система (горизонтальная поверхность), координата (процесс) остается постоянной.
| t |
| x0 |
| X |
Эти примеры являются механической аналогией понятия устойчивости. Рассмотрим математическое определение понятия устойчивости.
| u(t) |
| Д.У. |
| y(t) |
| U(s) |
| W(s) |
| Y(s) |
Система описывается дифференциальным уравнением:






Строго устойчивость определяется в смысле Ляпунова. Для линейных систем с постоянными параметрами считается, что система устойчива, если предел свободной составляющей равен 0

Устойчивость — внутреннее свойство системы, присущее ей вне зависимости от действующих на нее сигналов, поэтому рассматривается только свободная составляющая.
Это есть определение асимптотической устойчивости.
Свяжем требование устойчивости с расположением корней характеристического уравнения:


вещественные обозначим 
комплексные – 
Рассмотрим свободные составляющие соответствующие различным корням.
1. Корень вещественный, положительный:
| +j |
| yсв |
 |
| + |
| пл.s |
| t |
| система неустойчива |
2. Корень вещественный, отрицательный:
 +j +j |
| +j |
| пл. s |
| + |
| yсв |
| t |
| система устойчива |
3. Корни комплексные, сопряженные, с положительной вещественной частью:
| +j |
 |
 |
| yсв |
 |
| + |
| пл. s |
| t |

4. Корни комплексные, сопряженные, с отрицательной вещественной частью:
| yсв |
| +j |
 |
 |
 |
| пл. s |
| + |
| t |

Условием устойчивости является расположение корней характеристического уравнения в левой полуплоскости.
Система на границе устойчивости, если корни на мнимой оси.
Устойчивость – необходимое условие функционирования системы, поэтому в курсе уделяется много внимания методам оценки устойчивости системы.
🔍 Видео
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Регуляторы и астатизмы | Утро с теорией управления, лекция 4Скачать

29) КРИТЕРИИ УСТОЙЧИВОСТИ. КРИТЕРИЙ ГУРВИЦАСкачать

Теория автоматического управления. Лекция 12. D-разбиениеСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

10. Линейные однородные рекуррентные соотношения. Дискретная математикаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Теория автоматического управления. Лекция 23. Корневой метод Соколова Т.Н.Скачать