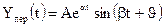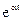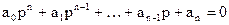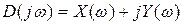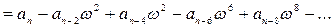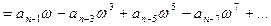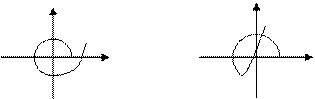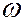Корни характеристического уравнения на комплексной плоскости (2 видео)

Содержание

Критерии устойчивости (Лекция)
Корневые критерии устойчивости
Корни характеристического уравнения на комплексной плоскости
💥 Видео

Видео:Решение уравнений на комплексной плоскостиСкачать

Критерии устойчивости (Лекция)

2. Корневой критерий

3. Критерий Стодолы

4. Критерий Гурвица

5. Критерий Михайлова

6. Критерий Найквиста

7. Показатели качества

8. Прямые показатели качества

9. Корневые показатели качества

10. Частотные показатели качества

Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.

Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:

1) корневой критерий,

2) критерий Стодолы,

3) критерий Гурвица,

4) критерий Найквиста,

5) критерий Михайлова и др.

Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.

2. Корневой критерий

Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.

Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.

Виды корней характеристического уравнения:

положительные (корень № 1);

комплексные сопряженные (4);

По кратности корни бывают:

одиночные (1, 2, 3);

сопряженные (4, 5): s_i = a ± j w ;

Корневой критерий формулируется следующим образом:

Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.

Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.

Пример 4.1. Передаточная функция системы имеет вид:

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.

Следовательно, система устойчива.

3. Критерий Стодолы

Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.

То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.

4. Критерий Гурвица

Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.

W_p — передаточная функция регулятора,

W_y — передаточная функция объекта управления.

Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы): W _¥ = W_p W_y .

Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

Тогда после подстановки и преобразования получаем:

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W _¥ :

D _з( s ) = A ( s ) + B ( s ).

Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с a_n ₊₁ по a ₀. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a ₀, a ₂, a ₄… или a ₁, a ₃, a ₅ …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.

Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.

Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.

Пример. Дана передаточная функция разомкнутой системы

Требуется определить устойчивость замкнутой системы по критерию Гурвица .

Для этого определяется ХПЗС :

D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.

Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а₄ = 2, а₃ = 5, а₂ = 10, а₁ = 6, а₀ = 1.

Матрица имеет вид:

(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Поскольку все определители положительны, то АСР устойчива.

5. Критерий Михайлова

Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

где t — запаздывание.

В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.

Порядок применения критерия Михайлова:

1) Записывается характеристическое выражение замкнутой системы:

D _з (s) = A(s) + B(s) . e — t s .

2) Подставляется s = j w : D _з (j w ) =Re( w ) + Im( w ).

3) Записывается уравнение годографа Михайлова D _з( j w ) и строится кривая на комплексной плоскости.

Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n — степень характеристического полинома.

Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.

6. Критерий Найквиста

Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.

1) Определяется передаточная функция разомкнутой системы .

2) Определяется число правых корней m .

3) Подставляется s = j w : W _¥ ( j w ).

4) Строится АФХ разомкнутой системы.

Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W _¥ ( j w ) m раз охватывала точку (-1; 0), где m — число правых корней разомкнутой системы.

Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.

В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W _¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).

7. Показатели качества

Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.

Показатели качества разбиты на 4 группы:

1) прямые — определяемые непосредственно по кривой переходного процесса,

2) корневые — определяемые по корням характеристического полинома,

3) частотные — по частотным характеристикам,

4) интегральные — получаемые путем интегрирования функций.

8. Прямые показатели качества

К ним относятся: степень затухания y , перерегулирование s , статическая ошибка е_ст, время регулирования t_p и др.

Рис. 4.4

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).

Сразу по ней определяется установившееся значение выходной величины у_уст.

Степень затухания y определяется по формуле

где А₁ и А₃ — соответственно 1-я и 3-я амплитуды переходной кривой.

Перерегулирование s = , где y_max — максимум переходной кривой.

Статическая ошибка е_ст = х — у_уст, где х — входная величина.

Время достижения первого максимума t _м определяется по графику.

Время регулирования t_p определяется следующим образом: Находится допустимое отклонение D = 5% у_уст и строится «трубка» толщиной 2 D . Время t_p соответствует последней точке пересечения y ( t ) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.

9. Корневые показатели качества

К ним относятся: степень колебательности m , степень устойчивости h и др.

Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:

Степень устойчивости h определяется как граница, правее которой корней нет, т.е.

h = min ,

где Re ( s_i ) — действительная часть корня s_i .

Степень колебательности m рассчитывается через угол g : m = tg g . Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g — угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:

m = min .

10. Частотные показатели качества

Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.

По АФХ определяются запасы: D A — по амплитуде, D j — по фазе.

Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.

Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.

По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке М_Е как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.

Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:

; t_p = ; ; M = .

Видео:Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Корневые критерии устойчивости

1) отрицательная вещественная часть

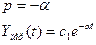
Устойчивая система.

2) положительные вещественные корни

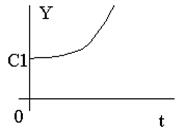
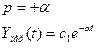
Неустойчивая система

3) корни комплексно-сопряженные с

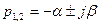
отрицательной вещественной частью

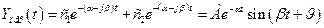
затухающие гармонические колебания

Система устойчива.

4) комплексно-сопряженные с положительной

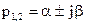
Неустойчивая система

5) комплексные корни (чисто мнимые)

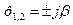
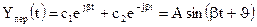Корни характеристического уравнения на комплексной плоскости

монотонный колебательный процесс

с постоянной частотой и амплитудой.

Система на границе устойчивости.

Вывод:Чтобы САУ была устойчивой необходимо, чтобы вещественные части корней были отрицательными. Если хотя бы один корень имеет положительную вещественную часть, то процесс будет расходящийся а система – неустойчива.

Если корень равен 0, то малейшее появление отрицательной составляющей сделает процесс устойчиво колебательным, а положительной – неустойчиво колебательным.

Часто корни характеристического уравнения при анализе устойчивости систем изображают на комплексной плоскости – плоскости корней характеристического уравнения

Комплексная плоскость мнимой осью разбивается на 2 части. Левую сторону называют областью устойчивости,а правую – областью неустойчивого движения.

Если корни лежат на мнимой оси или в 0, то система находится на границе устойчивости.

Вывод:Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней. Если хоть один корень справа, то система неустойчива. Таким образом, мнимая ось есть граница, за которую корни не должны переходить.

Если система имеет хотя бы один нулевой корень или хотя бы одну пару чисто мнимых корней, а все остальные корни имеют отрицательную вещественную часть, то система находится на границе устойчивости. При этом выделяют 3 типа границ устойчивости линейных систем:

1. Апериодическая граница устойчивости, которая соответствует р=0. Когда корень – нуль, то в характеристическом уравнении и система будет устойчива относительно скорости изменения управляемой величины, а сама управляющая величина может принимать произвольное значение. Система является нейтрально устойчивой.

2. Колебательная граница устойчивости, которой соответствуют чисто мнимые корни

В связи с тем, что корни характеристического уравнения определять трудно для систем высокого порядка, были разработан целый ряд критериев, с помощью которых судят об устойчивости систем.

Алгебраические критерии.

Критерий устойчивости Гурвица.

При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.

Необходимое условие является справедливым для всех систем:

Все коэффициенты характеристического уравнения должны быть положительными

Необходимое условие является и достаточным для систем 1-го и 2-го порядка.

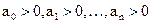
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):

Матрица коэффициентов

По диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а₁ до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс n, то на его место пишется 0.

а1 а3 а5 ………0 1=а1>0

а0 а2 а4 ………0 а1 а3

0 а1 а3 а5…. 0 2= а0 а2

………………. а1 а3 а5

…………………

Если аn=0 , то имеет место апериодическая граница устойчивости.

Если n₁=0, то это колебательная граница устойчивости.

Критерий Раусса.

Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица.

Для устойчивости систем по критерию Раусса необходимо и достаточно чтобы при а0>0 все коэффициенты первого столбца таблицы Раусса были положительными.

а₀	а₂	а₄	а₆	а₈
а₁	а₃	а₅	а₇	а₉
b₁	b₂	b₃	b₄
c₁	c₂	c₃	…	…
…	…	…	…	…

Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0

Частотные критерии

Критерий Михайлова.

Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до + .

Возьмём характеристический полином следующего вида:

(1)

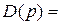
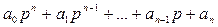
Подставим в него и выделим вещественную и мнимую части.

— вещественная часть,

— мнимая часть.

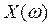
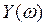
Изобразим годограф Михайловавыражения на комплексной плоскости.

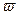
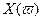
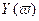
Берём значения и строим годограф. Для различных годограф имеет формы, представленные на рисунке. Эти годографы называются кривыми Михайлова.Кривая Михайлова строится по точкам, рассчитывается и для данной частоты, на кривой указываются значения частоты.

Формулировка критерия Михайлова.

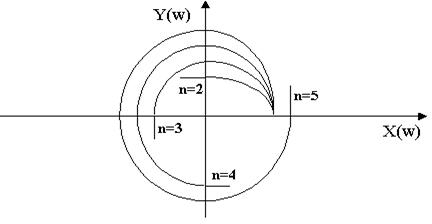
Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D(jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D(jω)=0

Другими словами, требуется, чтобы кривая Михайлова проходила последовательно квадрантов против часовой стрелки, всё время огибая начало координат и уходила в в том квадранте, номер которого соответствует показателю степени полинома. Если это условие не выполняется, то система является неустойчивой.

Устойчивая Неустойчивая Апериодическая Колебательная

граница устойчивости граница устойчивости

Другая формулировка критерия Михайлова:

Она состоит в использовании свойства перемежаемости корней многочленов 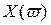и .

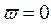
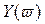
Идя по кривой Михайлова от т. в направлении возрастания частоты, мы выходим из оси , затем пересекаем ось , потом снова и т. д.

Это значит, что корни уравнений и должны следовать поочерёдно друг за другом.

Кривые и имеют приблизительно такой вид:

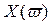
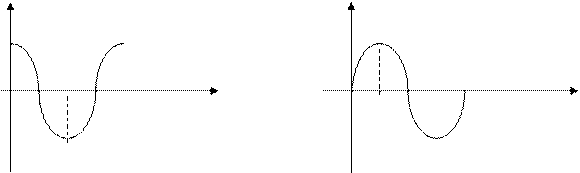
Перемежаться должны корни 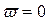, , ,… Между ними должно быть следующее соотношение:

Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Видео:Изобразить область на комплексной плоскостиСкачать

Корни характеристического уравнения на комплексной плоскости

12.1. Корневой метод оценки качества управления

Это косвенный метод, основанный на определении границ области расположения корней характеристического уравнения на комплексной плоскости, что дает возможность приблизительно оценить качество управления.

Пусть имеется дифференциальное уравнение замкнутой САУ:

Передаточная функция САУ

m — нули передаточной функции, p 1 , p 2 . p n — полюса передаточной функции.

Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ.

Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей:

Тогда уравнение динамики приобретает вид:

Общее решение данного уравнения имеет вид:

y(t) = y св + y вын = åA _i e pit + bо/a _n .

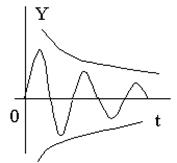
Время переходного процесса t пп определяется длительностью свободного процесса, который представляет собой сумму n экспоненциально затухающих составляющих (рис.88). Затухание каждой из составляющих определяется вещественной частью соответствующего плюса pi, которая для устойчивых систем должна быть отрицательна. Длительность переходного процесса определяется в основном свободной составляющей, имеющей наименьшее затухание, то есть наименьшее абсолютное значение вещественной части соответствующего полюса.

Если изобразить все полюса в комплексной плоскости корней (рис.89), то данный полюс (или пара комплексно сопряженных полюсов) будет наиболее близко расположен к мнимой оси.

Для приблизительной оценки качества САУ на плоскости корней выделяется область в виде трапеции, на сторонах которой находится хотя бы по одному корню, все остальные корни — внутри данной области. Эта область характеризуется параметрами: h — степень устойчивости (равна расстоянию от мнимой оси до ближайшего корня или пары комплексно сопряженных корней); m = tg(j) — колебательность (характеризует колебательность переходного процесса и величину перерегулирования); x — своего названия не имеет, равна вещественной части наиболее удаленного от мнимой оси корня.

По степени устойчивости h можно приблизительно вычислить время переходного процесса, которое определяется по моменту, когда свободная составляющая с наименьшим затуханием уменьшится до величины A _i , где A _i — начальное значение данной составляющей, то на рис.84:

y св ₃ (t) = A ₃ = A ₃ = > .

В общем случае, когда передаточная функция замкнутой САУ имеет нули, то использование данного метода может дать большую ошибку. Однако всегда качество управления будет тем лучше, чем больше h и меньше m , поэтому данный метод имеет смысл для любых САУ, но приближенно.

Зная значения h, x, m можно оценить область, за которую кривая переходного процесса выходить не будет (рис.90). Для этого строятся две кривые: u(t,h) — миноранта и v(t,h) — мажоранта, ограничивающая кривую переходного процесса соответственно снизу и сверху так, что u(t,h) e(t) v(t,h) , где e(t) = y _o -y(t) . Формулы для определения миноранты и мажоранты берутся в справочниках для конкретных случаев.

12.2. Интегральные критерии качества

Интегральные критерии позволяют судить о качестве управления путем вычисления интегралов от некоторых функций управляемой величины. Эта функция выбирается таким путем, чтобы значение определенного интеграла от этой функции по времени от 0 до + было однозначно связано с качеством переходного процесса. В то же время данный интеграл должен сравнительно просто вычисляться через коэффициенты уравнений исследуемой системы.

Например, если переходная характеристика является монотонной, то можно утверждать, что качество переходного процесса тем лучше, чем меньше площадь, ограниченная данной кривой и установившимся значением управляемой величины (рис.91). Она равна площади, ограниченной кривой изменения свободной составляющей управляемой величины и осью абсцисс.

Если система устойчива, то свободная составляющая управляемой величины в пределе стремится к нулю, поэтому площадь ограниченная данной кривой имеет конечное значение и определяется по формуле:

J_oo = .

Величина J_oo представляет собой линейную оценку качества управления .

Чем она меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум J_oo . Если имеется какой то варьируемы параметр A , то можно построить кривую J_oo = f(A) (рис.92). Ее минимум, определяемый из условия dJ_oo/dA = 0 , даст оптимальное значение A .

Пусть дано уравнение динамики замкнутой САУ:

Свободный процесс описывается однородным дифференциальным уравнением:

(a ₀ p n + a ₁ p n-1 + . + a _n )y св = 0,

y св =

J_oo = св(t)dt = .

Пусть при t = 0 САУ имела следующие начальные условия:

y св (0) = y ₀ , = y ₀ ’, . = y ₀ (n-1) .

y св () = 0,() = 0. () = 0,

так как процесс затухает и при t свободная составляющая и все производные становятся равны нулю. Подставляя эти значение, получаем:

То есть линейную оценку качества регулирования можно легко вычислить, зная начальные условия и коэффициенты дифференциального уравнения. Возможны и другие линейные оценки качества, но они используются реже, например:

J ₀₁ = св(t)tdt;

J 0n = св(t)t n dt.

Линейные оценки качества неприменимы при колебательном процессе. Так как площади, ограниченные кривой y св (t) и осью абсцисс складываются с учетом знака, то минимальному значению J_oo может соответствовать процесс с большим числом колебаний и малым быстродействием (рис.93). В этом случае более эффективны квадратичные оценки качества , например,

J 20 = y св 2 (t)dt .

Значение этого интеграла соответствует площади под кривой y св ₂ (t) и осью абсцисс, которая всегда положительна (рис.94).

Выбирая параметры САУ по минимуму J 20 мы приближаем кривую y св (t) к осям координат, что приводит к уменьшению времени регулирования (рис.95). Вывод формулы для вычисления этой оценки сложен, поэтому ограничимся замечанием, что значение вычисляется через коэффициенты дифференциального уравнения a ₀ . a _n ,b ₀ . b _m . При вычислении слагаемых в этой формуле используются определители Гурвица, так что даже расчет по ней сопряжен с определенными трудностями и требует использования ЭВМ или специальных таблиц.

При выборе параметров САУ по минимуму J 20 часто получают нежелательную колебательность процесса, так как приближение y св (t) к оси ординат вызывает резкое увеличение начальной скорости, что в свою очередь может вызвать большое перерегулирование, уменьшив при этом запас устойчивости. Для того, чтобы обеспечить плавность протекания процесса, в квадратичную оценку качества добавляется слагаемое, зависящее от скорости изменения регулируемого параметра y св ’(t). Получаем критерий качества

J ₂₁ = св ₂ (t) + t ₂ (y св ’(t)) ₂ ]dt,

где — некоторая наперед заданная постоянная времени, определяющая весовое соотношение между оценкой по y св и по y св ’. При малых значениях уменьшение колебательности будет незначительным. Завышение увеличит время переходного процесса так, что ее выбор определяется конкретными условиями.

Этот интеграл имеет наименьшее значение, если переходный процесс соответствует экспоненте с постоянной времени (рис.96). Другими словами, по соображениям качества управления следует стремиться к тому, чтобы переходная характеристика замкнутой САУ как можно меньше отличалась от характеристики инерционного звена первого порядка, имеющего наперед заданную постоянную времени , значение которой определяются техническими условиями.

Задача выбора параметров САУ по минимуму J ₂₀ и J 21 решается аналитически только в случае невысокого порядка дифференциального уравнения. Иначе используют ЭВМ.

Как влияет на качество управления близость корня характеристического полинома САУ к мнимой оси комплексной плоскости?
Как влияет на качество управления угол раскрытия трапеции области корней?
Как определить степень устойчивости САУ?
Как определить колебательность САУ?
Как можно вычислить время переходного процесса, зная как расположены корни характеристического полинома на комплексной плоскости?
Как построить мажоранту и миноранту, ограничивающую кривую переходного процесса САУ?
Что называется интегральными критериями качества САУ?
Как определить линейную и квадратичную оценки качества управления?
В чем недостатки линейной и квадратичной оценок качества управления?
Как выглядит оценка качества управления, способствующая приближению кривой переходного процесса к экспоненте?