Характеристический полином матрицы A , вычисляется следующим образом:
| A − λ E |
где E — единичная матрица, размеры которой совпадают с размерами исходной матрицы A .
Разберем подробнее приведенную выше формулу. Если матрица A задана в виде:
тогда выражение A − λ E имеет вид:
Наконец, нам нужно найти определитель:
Раскрыв этот определитель, мы получим полином n -ой степени ( n — порядок исходной матрицы), зависящий от λ :
P   ( λ ) = c n λ   n + c n − 1 λ   n − 1 + . + c i λ   i + . + c 1 λ   + c 0
Поскольку для вычисления характеристического полинома, требуется нахождение определителя матрицы, то характеристический полином может быть найден только для квадратной матрицы.
Наш онлайн калькулятор находит характеристический полином матрицы, причем в качестве элементов матрицы, можно вводить не только числа и дроби, но и параметры.
- Корни характеристического уравнения
- Матричный калькулятор онлайн
- Предупреждение
- Инструкция матричного онлайн калькулятора
- Вычисление суммы, разности, произведения матриц онлайн
- Вычисление обратной матрицы онлайн
- Вычисление определителя матрицы онлайн
- Вычисление ранга матрицы онлайн
- Вычисление псевдообратной матрицы онлайн
- Удаление линейно зависимых строк или столбцов матрицы онлайн
- Скелетное разложение матрицы онлайн
- Решение матричного уравнения или системы линейных уравнений AX=B онлайн
- Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
- LU-разложение или LUP-разложение матрицы онлайн
- Построение ядра (нуль-пространства) матрицы онлайн
- Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
- 🎦 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать

Корни характеристического уравнения
| Исходная матрица |
| Характеристическая матрица |
| Характеристический полином |
| Его корни |
По заданным элементам матрицы вычисляется его характеристическое уравнение, и находятся его корни. Ограничение сверху — матрица не больше 4 на 4, так как только для уравнения 4 степени, создан калькулятор.
Чем хорош данный калькулятор? Тем что работает в поле комплексных чисел, то есть исходные данные могут быть и вещественными и мнимыми.
Кроме этого, кроме значений можно писать любое математическое уравнение, которое корректно вычислется универсальным калькулятором комплексных чисел, что очень упрощает работу
Для чего нужны характеристические уравнения?
— Приведение поверхности или кривой 2 порядка в канонический вид
— Исследование дифференциальных уравнений на устойчивость
— Определение Жордановой формы матрицы
и многое другое.
Рассмотрим несколько примеров:
Найти общее характеристическое уравнение и его корни, если дана матрица
Введя данные слева направо, сверху снизу мы получим следующий результат
| Исходная матрица |
| Характеристическая матрица |
| Характеристический полином |
| Его корни |
Корни полинома 2, 3 и 6. Идет небольшая погрешность, в 15 знаке, но я считаю что это некритично.
Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Матричный калькулятор онлайн
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Характеристическое уравнение в ДУСкачать

Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы 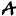
Кнопка 



При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы 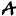
Видео:Матрицы: начало. Высшая математикаСкачать

Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Видео:Пример действий над матрицами (4): многочлен от матрицы.Скачать

Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «обратное «.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Видео:Собственные значения матрицыСкачать

Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Видео:Матричный метод решения систем уравненийСкачать

Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Видео:Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Видео:Для чего матрицы в жизни? | Высшая математика | TutorOnlineСкачать

Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы 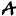
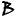
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
Видео:Многочлены от матрицСкачать

LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Видео:Как избавиться от характеристического многочленаСкачать

Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».
🎦 Видео
Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Характеристический многочлен. ТемаСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать


