Угол поворота в градусах (если положительное то против часовой стрелки)
Точка относительно которой проводится поворот
Новые координаты полученные при повороте фигуры(точки) на заданный угол
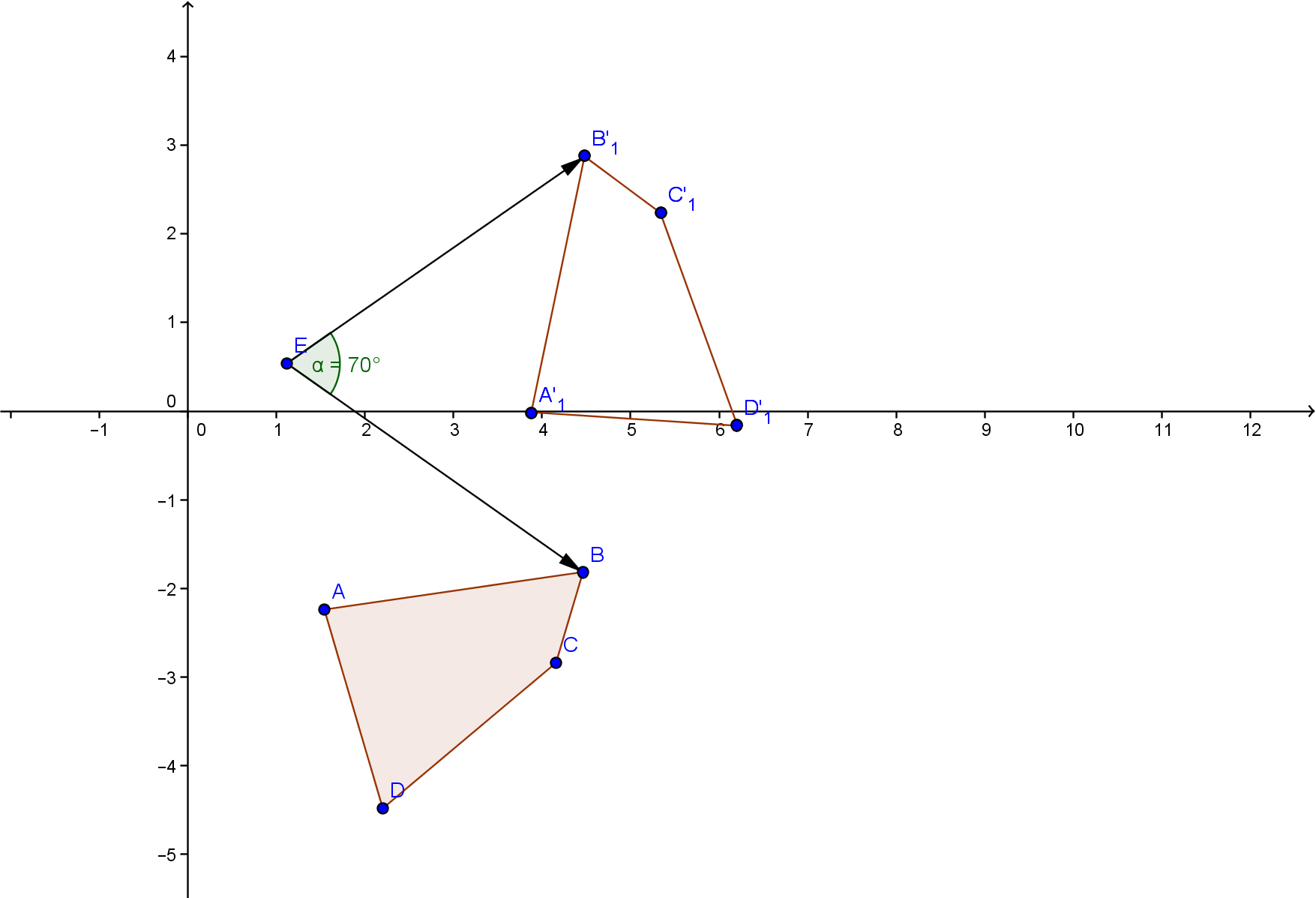
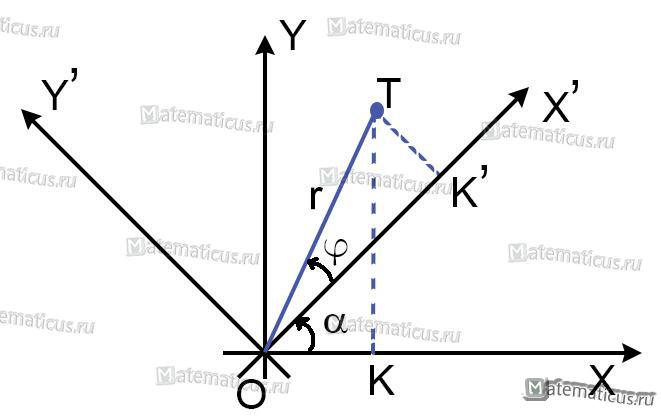
Поворот — это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.
Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать
Синтаксис
Координаты — строка, содержащая координаты в виде x:y (где x — абсцисса координаты, y — ордината координаты), разделенные хотя бы одним пробелом
Точка вращения — точка, относительно которой будет осуществляться поворот, всех заданных координат.
Поворот в градусах — поворот фигуры на заданный угол. Если число положительное — то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке.
Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать
Примеры
Пример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7)
Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3
Видео:Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать
Поворот осей координат
Чтобы найти поворот осей, зададим две системы координат, согласно рисунку
Пусть точка T в новой полярной системе координат имеет полярный радиус r и полярный угол φ. В старой полярной системе координат полярный угол точки T будет равен α+φ, а полярный радиус r будет как в новой системе координат.
Тогда уравнения примут вид:
x = r cos(α+φ)
y = r sin(α+φ)
Применяя тригонометрические тождества суммы двух углов для синуса и косинуса , получим выражения:
x = r (cosα cosφ — sinα sinφ) = r (cosφ) cosα — (r sinφ) sinα
y = r (sinα cosφ — cosα sinφ) = r (cosφ) sinα — (r sinφ) cosα
X =r cosφ и Y = r sinφ
Получим уравнения поворота осей координат
x = X cosα — Y sinα
y = X sinα — Y cosα
Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать
Если обозначим следующим образом
x = OK , y = KT — старые координаты точки T x´= OK´, y´ = KT´ — новые координаты точки T α — угол поворота осей
тогда ф ормулы поворота осей координат примут вид:
Пример До поворота осей на угол -30 0 точка L имела абсциссу x=2 и ординату y=0
Требуется найти координаты точки L после поворота осей.
Решение Подставляя в формулу, находим новые координаты осей x´, y´
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
Двумерный алгоритм преобразование в новые координаты
Видео:Составляем уравнение прямой по точкамСкачать
Поворот.
Пусть необходимо повернуть точку P(x, y) вокруг начала координат O на угол (фи) . Изображение новой точки на рис. 2.2. обозначим через P’(x’, y’). Всегда существуют четыре числа a, b, c, d, такие, что новые координаты могут быть вычислены по значениям старых координат x и y из следующей системы уравнений:
(2.1)
Для получения значений a, b, c, d рассмотрим вначале точку (x, y) = (1, 0). Полагая x =1 и y =0 в уравнении (2.1), получим
Но в этом простом случае, как это видно из рис. 2.3(а), значения x’ и y’ равны соответственно Cos (фи) и Sin (фи). Тогда будем иметь:
Аналогичным образом из рис. 2.3(б) следует
Тогда вместо системы уравнений (2.1) можем записать
(2.2)
Система уравнений (2.2) описывает поворот вокруг точки O — начала системы координат. Но часто это не то, что нам нужно. Если требуется выполнить поворот относительно заданной точки, то в этих уравнениях можно заменить: x — на (x-xo) , y — на (y-yo), x’ — на (x`-xo) и y’ — на (y`-yo) (сдвигаем систему координат) .
Система уравнений, которая описывает поворот точки вокруг любой точки:
(2.3)
Система уравнений (2.3) неудобна для реализации на PC. Применяем матричную запись.
(2.1) 
(2.2) 
(2.3)
