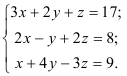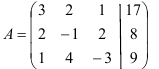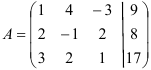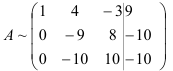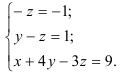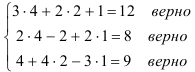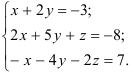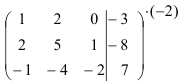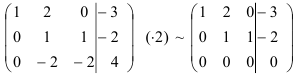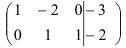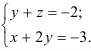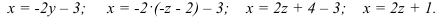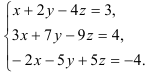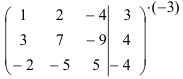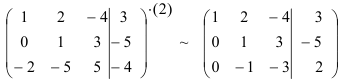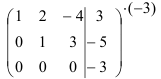Системы линейных уравнений
Задание: Решение систем линейных уравнений по правилу Крамера и методом Гаусса.
Цель: формирование умения решать системы линейных уравнений по правилу Крамера и методом Гаусса.
Задание для самостоятельной внеаудиторной работы:
5.1. Изучите теоретические основы решения системы линейных уравнений по правилу Крамера и методом Гаусса.
5.2. Решите систему уравнений, используя правило Крамера:
5.3. Решите систему линейных уравнений по методу Гаусса:
5.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?
Методические указания по выполнению работы:
Для решения систем линейных уравнений применяют правило Крамера и метод Гаусса.
1. Правило Крамера решения системы 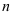
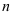
Система 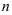
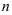

где 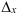

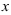
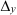

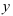
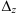

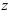
- Пример 1.
- Пример 2.
- Пример 3.
- Пример 4.
- Контрольная работа «Методы решения систем линейных уравнений»
- СПИСОК ЛИТЕРАТУРЫ
- Мерзляк 7 класс Контрольная 7
- Алгебра 7 класс (УМК Мерзляк) Контрольная работа № 7
- Вариант 1
- Вариант 2
- Вариант 3
- Вариант 4
- Мерзляк 7 класс Контрольная 7: 1 комментарий
- Добавить комментарий Отменить ответ
- Предметы
- Новые работы
- Найти контрольную:
- Авторы работ и УМК
- Предметы
- Важные страницы
- Популярное
- Предупреждение
- 💥 Видео
Пример 1.
Решите систему уравнений по правилу Крамера:
Решение:
Составим определитель 
Определитель 
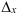
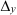
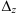
По правилу Крамера найдем неизвестные:
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
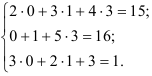
Итак, решение системы найдено правильно.
Ответ:
2. Метод Гаусса решения систем линейных уравнений
- Составьте расширенную матрицу системы — матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов.
- С помощью элементарных преобразований приведите полученную матрицу к ступенчатому виду.
- Восстановите систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и найдите значения неизвестных.
Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:
- число уравнений не равно числу неизвестных.
- если в правиле Крамера
.
Ответ на вопрос о существовании и количестве решений системы линейных уравнений дает теорема Кронекера-Капелли (критерий совместности системы линейных уравнений): система линейных уравнений с 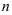
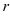
- если
(ранг матрицы равен числу неизвестных), то система имеет единственное решение;
- если
(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
Все возможные случаи решения системы линейных уравнений (одно решение, нет решений, множество решений) разобраны в примерах 2-4.
Пример 2.
Решите систему уравнений методом Гаусса:
Решение:
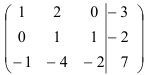
Выпишем расширенную матрицу системы и приведем её к ступенчатому виду:
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов
при последующих вычислениях.
Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом 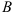
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:
Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:
Восстановим из полученной матрицы 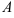
Из последнего уравнения находим: 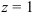
Подставим 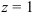
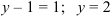
После подстановки 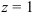
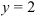
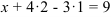
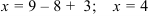
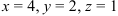
Следовательно, решение системы найдено верно.
Ответ: 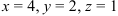
Пример 3.
Найдите все решения системы линейных уравнений:
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-2) и сложим ее со второй строкой:
Сложим первую и третью строки:
Домножим вторую строку на 2 и сложим ее с третьей строкой:
Вычеркнем нулевую строку:
Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум. Следовательно, в силу критерия Кронеккера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (три), то система имеет бесчисленное множество решений. Найдем эти решения.
Восстановим систему уравнений, равносильную исходной:
Пусть 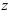
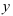
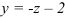
Подставим данное выражение 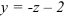
Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: 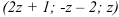
Ответ: 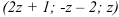
Пример 4.
Докажите, что система линейных уравнений не имеет решений:
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-3) и сложим ее со второй строкой:
Домножим первую строку на 2 и сложим ее с третьей строкой:
Сложим вторую и третью строки:
Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронеккера-Капелли, система не имеет решений.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. Контрольная №7. 7 классСкачать

Контрольная работа «Методы решения систем линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Контрольная работа №1
Системы линейных уравнений ТЕМА 1. Системы линейных уравнений.
Матрицы и действия с ними.
Определители и их основные свойства.
Методы решения систем линейных уравнений.
Видео:Контрольная работа №7 по алгебре, 7 класс. Система линейных уравненийСкачать

СПИСОК ЛИТЕРАТУРЫ
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. — М.: Физматлит, 2002. – 317 с.
Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: — М.: Физматлит, 2003. – 303 с.
Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.
Решение типового варианта контрольной работы.
Задача 1. Вычислить определитель 
Решение. Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Решим систему матричным способом, для этого вычислим обратную матрицу 


Решим систему методом Крамера. Главный определитель системы:


Запишем и вычислим вспомогательные определители

Ответ:
Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.



Таким образом, система равносильна системе
Находим
Ответ: 

При решении всеми методами одной и той же системы, мы получим один ответ.
Задача 3. Выполнить действия:
Решение. Выполним решение по действиям.



Ответ: 
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Если 





Пример:
Произведение 
Произведение 
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:

Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Мерзляк 7 класс Контрольная 7
Контрольная работа по алгебре в 7 классе «Системы линейных уравнений с двумя переменными» для УМК Мерзляк, Полонский, Якир. Ответов нет. Алгебра. Мерзляк 7 класс Контрольная 7 (4 варианта).
Алгебра 7 класс (УМК Мерзляк)
Контрольная работа № 7
Системы линейных уравнений с двумя переменными
Вариант 1
- Решите методом подстановки систему уравнений
< х + 3у = 13,
< 2х + у = 6. - Решите методом сложения систему уравнений
< 2х + 3у = 7,
< 7x – 3y = 11 - Решите графически систему уравнений
< х + у = 5,
< 4х – у = 10. - За 5 кг огурцов и 4 кг помидоров заплатили 220 р. Сколько стоит килограмм огурцов и сколько стоит килограмм помидоров, если 4 кг огурцов дороже кило грамма помидоров на 50 р.?
- Решите систему уравнений:
1) < 6х + 11у = 107,
< 5х – 2у = 11;
2) < 5х – 6у = 9,
< 15х – 18у = 26. - При каком значении а система уравнений
< 4х – aу = 3,
< 20х + 10у = 15
имеет бесконечно много решений?
Вариант 2
- Решите методом подстановки систему уравнений
< х + 5у = 15,
< 2х – у = 8. - Решите методом сложения систему уравнений
< 4х – 7у = 1,
< 2x + 7y = 11. - Решите графически систему уравнений
< х – у = 3,
< 3х – у = 13. - Масса 2 слитков олова и 5 слитков свинца равна 33 кг. Какова масса слитка олова и какова масса слитка свинца, если масса 6 слитков олова на 19 кг больше массы слитка свинца?
- Решите систему уравнений:
1) < 5х – 3у = 21,
< 3х + 2 у = 5;
2) < 2х – 3у = 2,
< 8х – 12у = 7. - При каком значении а система уравнений
< 3х + ау = 4,
< 6х – 2у = 8
имеет бесконечно много решений?
Вариант 3
- Решите методом подстановки систему уравнений
< 2х + у = 3,
< 3х + 2у = 2. - Решите методом сложения систему уравнений
< 4х + 5у = 2,
< 3х – 5у = 19. - Решите графически систему уравнений
< х + у = 4,
< х – 2у = –2. - За 8 тетрадей и 5 ручек заплатили 171 р. Сколько стоит тетрадь и сколько стоит ручка, если 3 тетради дороже ручки на 21 р.?
- Решите систему уравнений:
1) < 7х – 3у =–5,
< 3х + 4у = –18;
2) < 3х + 7у = 9,
< 6х +14у = 20. - При каком значении а система уравнений
< х + 2у = 6,
< 3х – ау = 18
имеет бесконечно много решений?
Вариант 4
- Решите методом подстановки систему уравнений
< х – 2у = 14,
< 2х + 5у = 1. - Решите методом сложения систему уравнений
< 7х – у = 10,
< 5x + y = 2. - Решите графически систему уравнений
< х – у = –3,
< x + 3y = 1. - Масса 8 пакетов муки и 3 пакетов сахара равна 30 кг. Какова масса пакета муки и какова масса пакета сахара, если масса 5 пакетов муки на 13 кг больше массы пакета сахара?
- Решите систему уравнений:
1) < 7х + 6у = 29,
< 3х – 5у = 20;
2) < 4х + 5у = 12,
< 8х + 10у = 22. - При каком значении а система уравнений
< 2х + 3у = 5,
< ах – 6у = –10
имеет бесконечно много решений?
Вы смотрели: Алгебра. Мерзляк 7 класс Контрольная 7 в 4-х вариантах. Контрольная работа по алгебре «Системы линейных уравнений с двумя переменными» по УМК Мерзляк, Полонский, Якир. Цитаты из пособия «Алгебра 7 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Мерзляк 7 класс Контрольная 7: 1 комментарий
Можно ответы на 1и 2 вариант
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Предметы
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Новые работы
Видео:7 класс. Системы линейных уравнений. Способ сложения. Решение контрольной работы А1-А2. Ершова А.П.Скачать

Найти контрольную:
Видео:Решение систем уравнений методом подстановкиСкачать

Авторы работ и УМК
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Предметы
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Важные страницы
Соглашение о конфиденциальности
(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Видео:Подготовка к контрольной работе "Матрицы и системы линейных уравнений"Скачать

Популярное
Видео:Подготовка к 9 контрольной работе (системы линейных уравнений ) , алгебра 7.Скачать

Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
💥 Видео
Контрольная работа 1 "Линейные уравнения" вариант 1. Алгебра 7 класс. Мерзляк. РешениеСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение системы уравнений методом ГауссаСкачать

7 класс. Контрольная №9 (из 10). Тема: Системы линейных уравнений. Разбираемся в методах! :)Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Контрольная работа 1Скачать

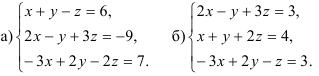
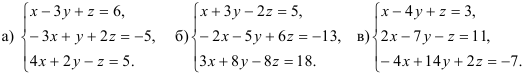
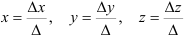

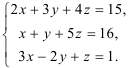
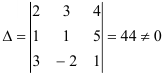
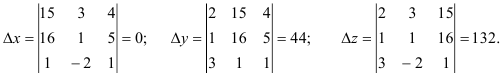
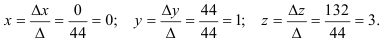
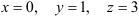
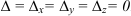 .
.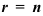 (ранг матрицы равен числу неизвестных), то система имеет единственное решение;
(ранг матрицы равен числу неизвестных), то система имеет единственное решение;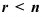 (ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.