Контрольная работа уравнение касательной к графику функции 10 класс

Контрольная работа № 7 по алгебре для 10 класса «Производная. Уравнение касательной» УМК Мерзляк Базовый уровень (два варианта). Цитаты из пособия «Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Базовый уровень» (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович, М.С.Якир, изд-во «Вентана-Граф») использованы на сайте в незначительных объемах, исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Алгебра 10 Мерзляк КР-7.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Алгебра 10 класс (Мерзляк)
Контрольная работа № 7.

Производная. Уравнение касательной.

КР-7. Вариант 1.

1. Найдите производную функции: 1) f (х) = 2х 5 – x 3 /3 + 3х 2 – 4; 2) f(x) = (3х – 5) √x; 3) f( x ) = ( x 2 + 9 x )/(х – 4); 4) f ( x ) = 2/ x 3 – 3/ x 6 .

2. Найдите уравнение касательной к графику функции f(x) = х 4 – 2х в точке с абсциссой х₀ = –1.

3. Найдите производную данной функции и вычислите её значение в данной точке х₀: 1) f(x) = √[3х + 1], х₀ = 5; 2) f (х) = sin 5 х, х₀ = π/3.

4. Материальная точка движется по координатной прямой по закону s(t) = – t 3 /3 + 2,5 t 2 + 24 t + 7 (время t измеряется в секундах, перемещение s – в метрах). Найдите скорость движения точки в момент времени t ₀ = 3.

5. Найдите уравнение касательной к графику функции f(x) = х 2 + 3х – 8, если эта касательная параллельна прямой у = 9х – 1.

КР-7. Вариант 2.

Вы смотрели: Контрольная работа № 7 по алгебре «Производная. Уравнение касательной» для 10 класса УМК Мерзляк Базовый уровень. Цитаты из пособия «Дидактические материалы. Алгебра и начала математического анализа. 10 класс. Базовый уровень». Алгебра 10 Мерзляк КР-7.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Алгебра 10 Мерзляк КР-7: 1 комментарий

А где можно найти ответы??

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Предметы

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Новые работы

Видео:Уравнение касательной к графику функции в задачах. Часть 1. Алгебра 10 классСкачать

Найти контрольную:

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Авторы работ и УМК

Видео:Уравнение касательнойСкачать

Предметы

Видео:Уравнение касательнойСкачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:Математика это не ИсламСкачать

Популярное

Видео:Алгебра 10 класс // Логарифмы // Контрольная работа // Решение, ответы // К учебнику АлимоваСкачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:Геометрический смысл производной. Уравнение касательнойСкачать

» Уравнение касательной к графику функции», 10 класс

Тип урока: изучение нового материала. Обучающиеся должны осознать большую практическую и историческую значимость производной.

Просмотр содержимого документа
«» Уравнение касательной к графику функции», 10 класс»

-Урок изучения нового материала в 10 классе

«Уравнение касательной к графику функции»

УМК: Алгебра и начала математического анализа. 10-11 классы

(базовый уровень) 2017 год

Авторы учебника: А.Г. Мордкович.

Тип урока: изучение нового материала

Тема: Уравнение касательной к графику функции

Цель: вывести формулу уравнения касательной к графику функции в заданной точке, составить алгоритм нахождения уравнения касательной, научиться составлять уравнение касательной.

отработать и систематизировать навыки и умения по теме «Касательная, уравнение касательной к графику функции».

способствовать развитию внимания;

способствовать развитию навыков устного счета;

способствовать развитию логического мышления, математической интуиции;

способствовать развитию и пониманию у учащихся меж предметных связей;

развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, умение аргументировать свою точку зрения);

создавать условия для осознания необходимости самостоятельных действий при решении проблем;

осознавать большую практическую и историческую значимость производной.

Оборудование: компьютер, проектор, презентация, учебник, программа «Живая математика», чертежи графиков функций в программе «Живая математика».

Структура и план урока:

1.Мотивация (самоопределение) к учебной деятельности.

2.Актуализация знаний и фиксация затруднения в деятельности.

3.Постановка учебной задачи.

4.Открытие нового знания.

7.Рефлексия деятельности (итог урока).

1.Мотивация (самоопределение) к учебной деятельности.

Прошу садиться! Тема сегодняшнего урока. «Уравнение касательной к графику функции». Слайд 1

2.Актуализация знаний и фиксация затруднения в деятельности.

Повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося (5-7 мин). Повторяем формулы производных и правила вычисления производных.

3.Постановка учебной задачи.

4.Открытие нового знания.

Задача 5 слайда презентации: Согласны ли вы с утверждением: «Касательная – это прямая, имеющая с данной кривой одну общую точку»? Посмотрим на графики. (слайд 6)

Чего мы еще не знаем? (1-2 мин) Учащиеся формулируют цели и задачи урока. Уточним цели и задачи урока. (слайд 7)

4.Открытие нового знания.

Слайд 8. Вернемся к известному графику. На графике проведена касательная, её уравнение задано формулой y= 2x-1. Давайте вспомним общий вид уравнения прямой. (y=kx+b). Так как касательная является прямой, то её уравнение будет иметь такой же вид. Но мы знаем, что касательная связана с производной в точке к функции, поэтому попытаемся связать коэффициенты уравнения k и b с функцией f(x) и её производной. k=tgµ=f`(a).Точка с координатами (a; f(a)) принадлежит графику функции и касательной, то есть её координаты удовлетворяют уравнению функции и уравнению касательной. Подставим их в уравнение касательной и найдём значение b. f(a)= f`(a)*a+b; b=f(a)- f`(a)*a; y= f`(a)x+ f(a)- f`(a)*a;

y=f(a)+ f`(a)(x-a) – уравнение касательной к графику функции.(слайды 9,10,11)

Алгоритм составления уравнения касательной к графику функции

Обозначить абсциссу точки касания буквой а.

3.Найти f`(х) и вычислить f`(a).

4. Подставить найденные числа а, f(a), f`(a)в формулу уравнения

y=f(a)+ f`(a)(x-a) (слайд 12)

Пример: у= 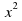, в точке а=1

Самостоятельная работа по группам (слайд 13 и 14)

Составить уравнение касательной к графику функции f(x)= 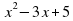в точке с абсциссой a= -1(у доски).

Слайды 15, 16, 17.

6.Самостоятельная работа (слайд 19)

ДОМАШНИМ ЗАДАНИЕМ будут номера 29.12, 29.5, отработать составление уравнения касательной, используя алгоритм.

8.Рефлексия деятельности (итог урока).

-Какую задачу ставили?

-Удалось ли решить поставленную задачу?

-Какие получили результаты?

-Где можно применить новые знания?

И, наконец, после «всяких умных вещей» немного юмора. На экране представлены графики зависимости уровня ваших знаний от времени, в интервале от начала урока до его завершения.

слайд 21

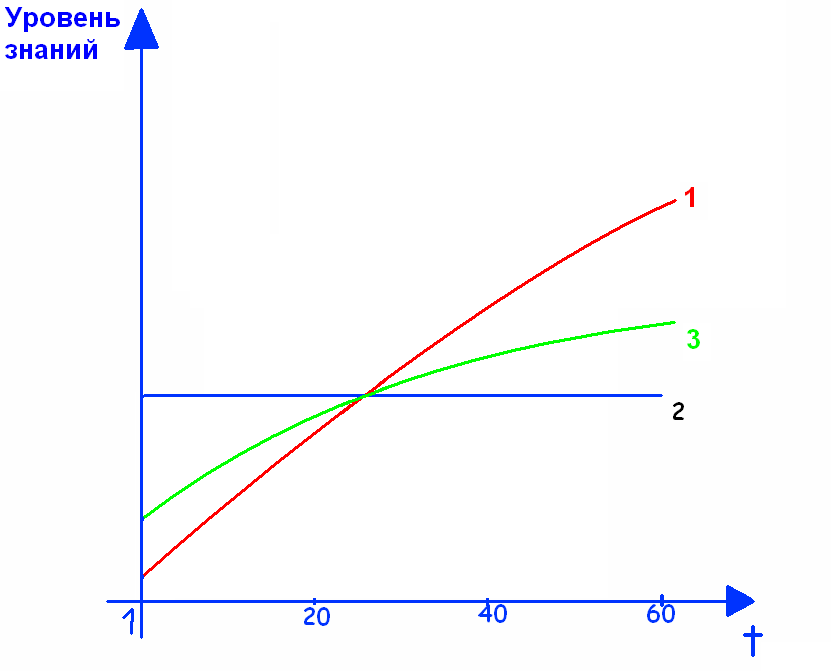
Пожалуйста, выберите тот график, который, на ваш взгляд, наиболее вам близок. Имеют ли они отношение к теме нашего урока? По этим графикам можно судить о скорости приращения ваших знаний в ходе урока. График 1 – мы достигли цели и решили задачи, поставленные в начале урока.

Спасибо за урок!

Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1,2. Учебник и задачник для учащихся общеобразовательных учреждений (базовый уровень)/ под ред. А. Г. Мордковича. — М.: Мнемозина, 2015.

Живая математика: сборник методических материалов. – М.: ИНТ. 176 с.

В. М. Чернявский Работа с программой «Живая математика».

Различные Интернет-ресурсы для поиска детьми дополнительной информации по теме «Производная».

Видео:Производная: касательная к графику.Скачать

«Уравнение касательной к графику функции», 10 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Презентация к уроку «Уравнение касательной к графику функции» Подготовила: С.А.Деревяга МБОУ Школа №67

Девиз урока: Плохих идей не бывает Мыслите творчески Рискуйте Не критикуйте

«Уравнение касательной к графику функции»

Восстанови текст f(x) fI(x) 0 -7×3+4×2+8 -21×2+8x sinx cosx -cosx sinx tgx -3cosx (x2+2) 3sinx (x2+2)-6xcosx (8x-15)5 40(8x-15)4 Sin3x 3sin2xcosx

х у -1 α у=кх+b К=tgα=2:4=0,5 b- точка пересечения с осью у У=0,5х-1 2 4 Задача 1. Записать уравнение прямой

Задача 2. Записать уравнение прямой у х α у=кх+b К=-tgα= — 4:5= — 0,8 b- точка пересечения с осью у А А(-1;2) 2= -0,8 (-1)+b b=2-0,8=1,2 У=-0,8х+1,2

Ответьте на вопросы: Какие из указанных прямых параллельны? у = 0,5х; у = — 0,5х; у = — 0,5х + 2. Почему? 2) Согласны ли вы с утверждением: «Касательная – это прямая, имеющая с данной кривой одну общую точку»?

1 x y y = x2 х = 1 y = 2х — 1 y x 1 2 3

Касательная есть предельное положение секущей при Δх → 0 = f ‘(a).

Уравнение касательной y = kx + b k = f / (x0) Найдём b y = f / (x0) · x + b f(x0) = f / (x0) · x0 + b b = f(x0) — f / (x0) · x0 y=f(x) x0 f(x0) M(x0; f(x0)) y = f(x0) + f / (x0) · (x — x0) y = f / (x0) · x+ f(x0) — f / (x0) · x0

Алгоритм: 1. Значение функции в точке касания f(x0) 2. Общая производная функции f / (x) 3. Значение производной в точке касания f / (x0) 4. Подставить найденные значения в общее уравнение касательной. y = f(x0) + f / (x0) · (x — x0)

Решение опорных задач: 1. Если задана точка касания Составить уравнение касательной к графику функции f(x) = x3 – 3x – 1 в точке М с абсциссой –2. 2. По ординате точки касания. Составить уравнение касательной в точке Графика с ординатой y0 = 1. 3. Заданного направления. Написать уравнения касательной к графику y = x3 – 2x + 7, параллельной прямой у = х. 4. Условия касания графика и прямой. При каких b прямая y = 0,5x + b является касательной к графику функции ?

5. При каких значениях аргумента производная функции, заданной графиком а) равна 0; б) больше 0; в) меньше 0?

6. На рисунке изображён график функции f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f /(x) в точке x0 .

Подведение итогов урока Что называется касательной к графику функции в точке? В чём заключается геометрический смысл производной? Сформулируйте алгоритм нахождения уравнения касательной в точке? С какими опорными задачами познакомились? Достигли ли цели урока?

«Синквейн» или «Сенкан». Сенкан – «белый стих», слоган из пяти строк (от фр. Cing – пять), в котором синтезирована основная информация. Структура сенкана. Существительное (тема). Два прилагательных (описание). Три глагола (действие). Фраза из четырех слов (описание). Существительное (перефразировка темы).

Домашнее задание п.43, №1,2 (устно), №3,22,30,(а,в), 32(а)

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 861 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 51 человек из 23 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Геометрический смысл производной | КасательнаяСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 433 материала в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 05.06.2017
• 1603
• 16

• 05.06.2017
• 536
• 3

• 05.06.2017
• 1241
• 3

• 05.06.2017
• 433
• 0

• 05.06.2017
• 656
• 1

• 05.06.2017
• 1559
• 24

• 05.06.2017
• 695
• 13

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 05.06.2017 1339
• PPTX 348.7 кбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Деревяга Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 7 месяцев
• Подписчики: 0
• Всего просмотров: 8692
• Всего материалов: 6

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте

Время чтения: 1 минута

Онлайн-конференция о профессиональном имидже педагога

Время чтения: 2 минуты

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎦 Видео

Математика 10 Класс (Алгебра и Геометрия)Скачать

Функция. 10 класс.Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Что такое касательная | Осторожно, спойлер! | Борис Трушин |Скачать

Не сдал ОГЭ Устное Собеседование shorts #shortsСкачать