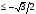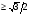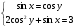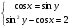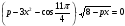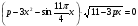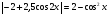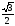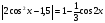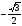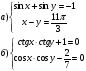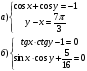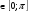Контрольная работа тригонометрические уравнения и неравенства 10 класс по вариантам

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Контрольная работа «Тригонометрические уравнения и неравенства»

Контрольная работа по алгебре 10 класса «Тригонометрические уравнения и неравенства» представлены в четырех вариантах. Эти тексты можно использовать как самостоятельные работы, как задания для индивидуальной работы.

Данные тексты контрольных работ уместны не только при изучении темы, но и при итоговой повторении в конце учебного года, и про итоговом повторении в рамках подготовки к ЕГЭ.

Просмотр содержимого документа
«Контрольная работа «Тригонометрические уравнения и неравенства»»

КОНТРОЛЬНАЯ РАБОТА «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»

Вариант № 1 Вариант № 2

а) 2 sin x + 5 cos x = 0

б) 2 sin 2 x + 3 sinx cosx – 3 cos 2 x = 1

в) sin 2x + cos 2 x = 1

г) sin x = cos 3x

д) cos 5x + cos 3x + cos x = 0

а) 3 sin x – 7 cos x = 0

б) 4 sin 2 x + sinx cosx – cos 2 x = 1

в) sin 2x + sin 2 x = 1

г) cos x = sin 3x

д) sin 5x + sin 3x – sin 4x = 0

а) cos x

б) tg x

в) 2 cos 2 x + sin x – 1

а) sin x

в) 2 sin 2 x – 5 cosx + 1 0

4) Решить уравнения и неравенства. (Дополнительное задание )

а) sin x – 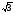cos x = 1

б) 3 + 2 sin 2x = tg x + ctg x

в) 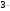(log₂sin x) 2 + log₂(1 – cos 2x) = 2

г) sin 2x + 2 sin x 0

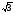
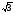
д) tg 2 x – 4 tg x + 0

е) lg log _cosx(7 – x) 0

5) Найти все значения р, при которых число х = 2 является корнем ур-ия.

Вариант № 3* Вариант № 4*( 2 ч. )

а) sin 2 x + sin 2 2x = sin 2 3x + sin 2 4x

б) 3 sin3x cos3x + 2 sin4x sin(п + x) = 3 sin5x cosx

в)

г) cos (2 sin x) =

д) sin 5 x – sin 4 x cosx = 2sin 3 x cos 2 x

е)

а) 1 – sin 4 x – 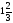cos 4 x = 0

б) 6 sin2x sin6x = 10 cos8x cos(п – x) + 3 cos 2 2x – 3 sin 2 2x

в)

г) sin (2 cos x) =

д) 3sin(x – п/4) = 2сos(x + п/3)

е)

2) Решить системы уравнений.

а) 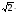(sin 2x – cos x) + 2 sin x 1 x

б) 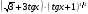0

в) 2 cos 2 (п/4 + x) – 3sin x cos x

г) 2 cos 2x – 9 sin x – 4 0 д)

а) 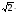(sin 2x + sin x) – 2 cos x

б) 0 в) 2sin 2 x + 5sin(п/4 + x)сos(п/4 + x) 0

г) 5 cos 2x + 22cos x + 9

4) При всех значениях параметра р решить.

а) б) cos 4x – 4 cos 4 x = р

5) При каких значениях параметра р уравнение tg (п/4 + х) + tg (п/4 – х) = 2р имеет решения?

6) При каких значениях параметра р уравнение не имеет корней?

Видео:Как решать тригонометрические неравенства?Скачать

Контрольная работа по алгебре и началам математического анализа для 10 класса по теме «Тригонометрические уравнения и неравенства»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

10 класс . Тригонометрические уравнения и неравенства. В – 1

При выполнении заданий 1 – 3 следует записать только ответ.

1. Вычислите .
Ответ: ______________________

2. Запишите решения уравнения х = – 1.

3. Решите уравнение: х + 1 = 0.

ІІ часть
Решение заданий 4 –6 может иметь краткую запись без обоснования

4. Решите уравнение:
а) 6 х = ; б) 5 х + х = 0.

5. Решите неравенство:
а) х > ; б) ( ) .

6. Решите уравнение:
а) х – 11 х – 1 = 0;
б) х – 2х – 2 х = 2;
в) х 3 х х = 0.

Решение 7 задания должно иметь обоснование, необходимо записать последовательные логические действия и объяснения

7. Решите уравнение: х + х = 2.

10 класс . Тригонометрические уравнения и неравенства. В – 2

При выполнении заданий 1 – 3 следует записать только ответ.

1. Вычислите .
Ответ: ______________________

2. Запишите решения уравнения х = 1.
Ответ: ______________________

3. Решите уравнение: х – 1 = 0.

ІІ часть
Решение заданий 4 – 6 может иметь краткую запись без обоснования

4. Решите уравнение:
а) 4 х = ; б) 3 х х = 0.

5. Решите неравенство:
а) х ; б) ( ) ≤ .

6. Решите уравнение:
а) 2 х + 7 х – 5 = 0;
б) х + 1,5 2х – 2 х = 1;
в) х + 3 х + х = 0.

Решение 7 задания должно иметь обоснование, необходимо записать последовательные логические действия и объяснения

7. Решите уравнение: х – х = 2.

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Контрольные работы «Тригонометрические уравнения и неравенства. Производная»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

Контрольные работы к учебнику «Алгебра и начала

математического анализа,10» С.М. Никольского и др.

Контрольная работа №1

Тригонометрические уравнения и неравенства

а) cos x =-1; б) sinx = ; в) ctgx =- .

2. а) sin 2 x + sinx -2=0; б) 3 sin 2 x — cosx +1=0.

3. a) sinx- cosx=0; б ) 3sin 2 x+2 sinx cosx+cos 2 x=0.

4. а) sin x =- 0,5; б) cos x = ; в) tgx =-3.

5 a) sinx+ cosx=1; б ) 2cos 2 x+sin4x=1.

6 Решите неравенство :

а) Sin x cos x >0,5; в) tgx ≤-3.

г ) 2cos 2 x+ sin x >2

7) sin 2x=cos 4 -sin 4

8) =6cos x-2

9) cos 9x-cos 7x+cos 3x-cos x=0

10) +3 cos 2 x =1-2 cos x

а) sinx =-1; б) cosx = ; в) tgx =- .

2. а ) cos 2 x-cos x-2=0; б ) 3cos 2 x-2sinx+2=0.

3. a) sinx+ cosx=0; б ) 3sin 2 x-2 sinx cosx +cos 2 x=0.

4. а) cos x =- 0,5; б) sin x = ; в) tg x =2

5 a) sinx- cosx=1; б ) 2cos 2 x-sin4x=1.

6 Решите неравенство

а ) Sin x>0,5; б )cos x

г ) 2sin 2 x- cos x >2

7) ctg x-sinx=2sin 2

8) =6sinx-1

9) 8-4sin 2 x=sin2x ctgx — 9cosx

10) sin x sin3x+sin4x sin8x=0

а) cos x =1; б) sinx = ; в) ctgx =- .

2. а ) 2 sin 2 x+sinx-1=0; б ) 3cos 2 x-sinx+1=0.

3. a) sinx- cosx=0; б ) sin 2 x+2 sinx cosx+3cos 2 x=0.

4. а) sin x = -0,6; б) cos x = ; в) tgx =-4

5 a) sinx+ cosx=-1; б ) 2cos 4x+cos 2 x=1.

6 Решите неравенство:

а ) Sin x>-0,5; б )cos x

г ) 4cos 2 x- (2 -2)sin x > 4-

7) sin 2x=cos 4 -sin 4

8) = +cos x

9) cos 9x-cos 7x+cos 3x-cos x=0

10) +3cos 2 x=1-2cos x

а) sin x =1; б) cosx = ; в) tgx =- .

2. а ) 2 cos 2 x-cosx-1=0; б ) 3sin 2 x-2cosx+2=0.

3. a) sinx+ cosx=0; б ) sin 2 x-2 sinx cosx+3cos 2 x=0.

4. а) cos x = -0,7 б) cos x = ; в) tg x =5

5 a) sinx- cosx=-1; б ) cos 4x-sin 2 x=1.

6 Решите неравенство:

а ) Sin x б )cos x>-0,5; tgx ≤ 2

г ) 4 sin 2 x+ (2 -2)cos x > 4-

7) ctg x-sinx=2sin 2

8) =6sinx-1

9) 8-4sin 2 x=sin2x ctgx — 9cosx

10) sin x sin3x+sin4x sin8x=0

Контрольная работа №2

а) ƒ(х)=6х 4 +5х 3 +3х 2 +3, х₀ =1; б) ƒ(х)=х со s x , х₀=

2. Найдите ƒ'(х), если:

а) ƒ(х)= ; б) ƒ(х)=7 7 3 ; в) ƒ(х)= log ₅ x ; г) ƒ(х) =

3.Вычислите значение производной функции у=с tg 3 x в точке х₀=

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 +3х 2 -9х-13 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)= — 6 3 4 ; б) ƒ(х)=e 3х+2 ; в) ƒ(х)=х√х 2 -3х+4

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=17+24х-4t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

8. Найдите производную функции

а) у=х 3 со s б) y = log ₈ (9 x +7)· arctg 2 3 x 4

в) y=cos —

а) ƒ(х)=3х 5 -12х 2 +6х+3, х₀ =1; б) ƒ(х)=х sinx х₀=

2. Найдите ƒ'(х), если:

а) ƒ(х)= ; б) ƒ(х)=5 5 3 ; в) ƒ(х)=5 x ; г) ƒ(х) =

3.Вычислите значение производной функции у= tg 4 x в точке х₀=-

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 -6х 2 +9х-11 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)= — 3 3 4 ; б) ƒ(х)= ln (3+2 x ); в) ƒ(х)=х√х 2 +2х+3

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=13+10t-5t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

ƒ(х)= ln

8. Найдите производную функции

а) у=х 2 со s б) y = log ₃ (9 x +7)· arcctg 2 x 3

в) y=sin —

а) ƒ(х)=-5х 4 +4х 3 +6х 2 -2 x +3, х₀ =1; б) ƒ(х)=х tgx х₀=

2. Найдите ƒ'(х), если:

а) ƒ(х)= ; б) ƒ(х)=5 5 4 ; в) ƒ(х)=10 x ; г) ƒ(х) =

3.Вычислите значение производной функции у= cos 3 x в точке х₀=-

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 -4х 2 +5х-17 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)= — 12 3 5 ; б) ƒ(х)= lg (4-3 x ); в) ƒ(х)=4х√3х 2 -2х+1

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=23+20t-5t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

ƒ(х)= ln

8. Найдите производную функции

а) у=х 3 со s б) y = log ₈ (9 x +7)· arctg 2 3 x 4

в) y=cos —

а) ƒ(х)=5х 3 -4х 4 +2х 2 -2 x +5, х₀ =1; б) ƒ(х)=х ctgx х₀=

2. Найдите ƒ'(х), если:

а) ƒ(х)= ; б) ƒ(х)=7 7 6 ; в) ƒ(х)= lg x ; г) ƒ(х) =

3.Вычислите значение производной функции у= sin 2 x в точке х₀=

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 +2х 2 -7х-13 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)= — 6 3 5 ; б) ƒ(х)=10 4 x -3 ); в) ƒ(х)=4х√4х 2 -2х+1

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=27+24t-2t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

8. Найдите производную функции

а) у=х 2 со s б) y = log ₃ (9 x +7)· arcctg 2 x 3

в) y=sin —

Краткое описание документа:

Методические материалы к контрольным работам по математике 10 класса «Тригонометрические уравнения и неравенства. Производная» представлены в четырех вариантах. Эти тексты можно использовать как самостоятельные работы, как задания для индивидуальной работы. Данные тексты контрольных работ уместны не только при изучении темы, но и при итоговой повторении в конце учебного года, и про итоговом повторении в рамках подготовки к ЕГЭ.

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Профессиональные компетенции педагога в рамках Федерального закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012

Курс повышения квалификации

Особенности методической работы в онлайн-образовании

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

• Сейчас обучается 51 человек из 25 регионов

«Домашнее обучение. Лайфхаки для родителей»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Видео:10 класс. Контрольная №4 (из 9). Тема: Тригонометрические уравнения и неравенства. Решаем, изучаем!Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 858 211 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 28.04.2015
• 1371
• 11

• 28.04.2015
• 708
• 0

• 28.04.2015
• 13513
• 34

• 28.04.2015
• 1207
• 0

• 28.04.2015
• 2357
• 0

• 28.04.2015
• 8153
• 161

• 28.04.2015
• 1742
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 28.04.2015 37965
• DOCX 162.5 кбайт
• 373 скачивания
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Максимович Надежда Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 5 месяцев
• Подписчики: 0
• Всего просмотров: 122982
• Всего материалов: 42

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Вспомни, что сказал учитель?. Упражнения для младших школьников на развитие памяти.»

«Развитие коммуникативных умений школьников посредством игровой технологии»

«Игра в архитектуру. «Благоустройство школьного двора или прилегающего к школе участка»»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

В школах России пройдет урок, посвященный Великой Отечественной войне

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Контрольная работа 1Скачать

Мерзляк 10 класс Контрольная 6

Алгебра. Мерзляк 10 класс Контрольная 6 в четырех вариантах. Контрольная работа по алгебре в 10 классе «Тригонометрические уравнения и неравенства» для УМК Мерзляк, Полонский, Якир (базовый уровень). Транскрипт заданий. Ответов нет!

Алгебра 10 класс (УМК Мерзляк)
Контрольная работа № 6

Тема: Тригонометрические уравнения и неравенства

Проверяемые темы (параграфы) учебника: 26) Уравнение cos x = b. 27) Уравнение sin x = b. 28) Уравнения tg x = b и ctg x = b. 29) Функции у = arccos x, у = arcsin x, у = arctg x и у = arcctg x. 30) Тригонометрические уравнения, сводящиеся к алгебраическим. 31) Решение тригонометрических уравнений методом разложения на множители. 32) Решение простейших тригонометрических неравенств.

Вариант 1 (транскрипт заданий)

№ 1. Решите уравнение: 1) sin 4х = –√2/2; 2) cos (х/2 – π/8) = 0; 3) cos 3x + cos 5x = 0.

№ 2. Решите неравенство: 1) cos 5x 2 х + 7sin х – 5 = 0; 2) 2sin 2 х + 1,5sin 2х – 3cos 2 х = 1; 3) sin 8х + sin 10 х + cos х = 0.

№ 4. Решите уравнение sin 2х + –√3cos 2х = 2cos 6х.

Ответов нет!

Вы смотрели: Алгебра. Мерзляк 10 класс Контрольная 6 в 4-х вариантах. Контрольная работа по математике в 10 классе «Тригонометрические уравнения и неравенства» для УМК Мерзляк, Полонский, Якир.

(с) Цитаты из пособия «Алгебра 10 класс. Методическое пособие / Е.В. Буцко и др. (базовый уровень)» использованы в учебных целях.

Видео:10 класс Контрольная работа База Тригонометрические уравнения Задание №6Скачать

Мерзляк 10 класс Контрольная 6: 1 комментарий

а где ответы, 10 А требует ответов

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

Предметы

Видео:10 класс Контрольная по тригонометрииСкачать

Новые работы

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Найти контрольную:

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Авторы работ и УМК

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Предметы

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:10 класс. Контрольная работа. База . Тригонометрические уравнения. Задание №4Скачать

Популярное

Видео:10 класс. Контрольная работа. База. Тригонометрические уравнения Задание №3Скачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

💡 Видео

Решение тригонометрических неравенств. 10 класс.Скачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Алгебра 10 класс. 29 октября. ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА! ЖЕСТЬ!Скачать

Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Алгебра, 10 класс, Подготовка к контрольной работе по теме "Тригонометрические функции"(Ш.А. Алимов)Скачать