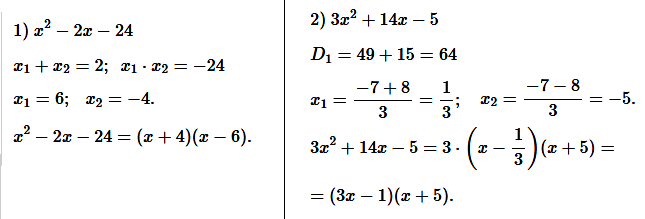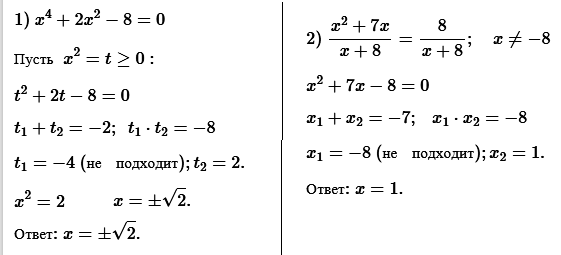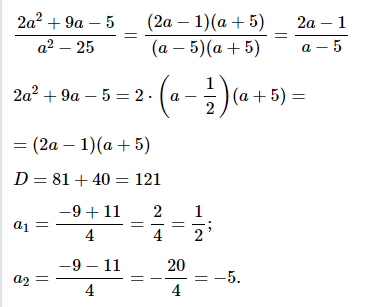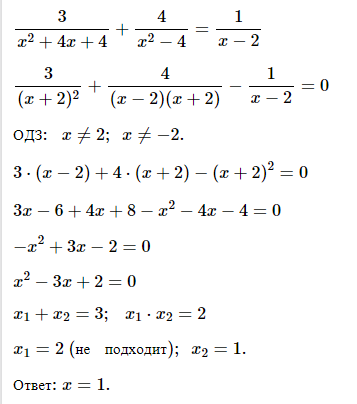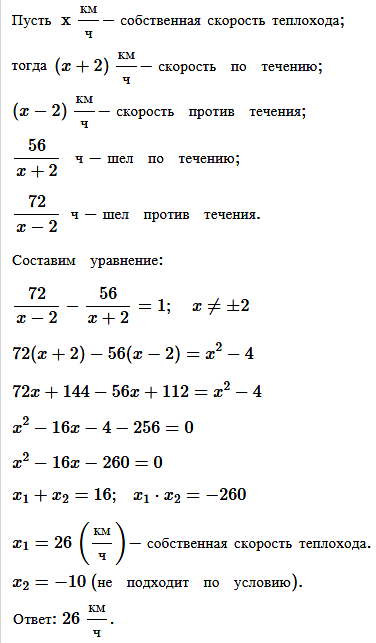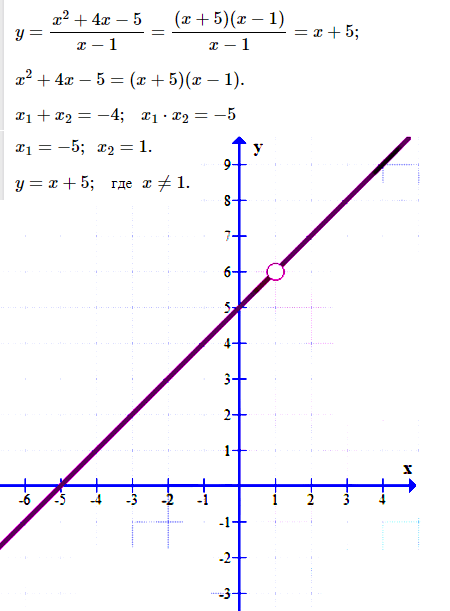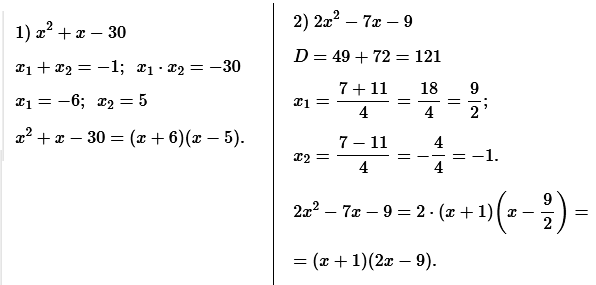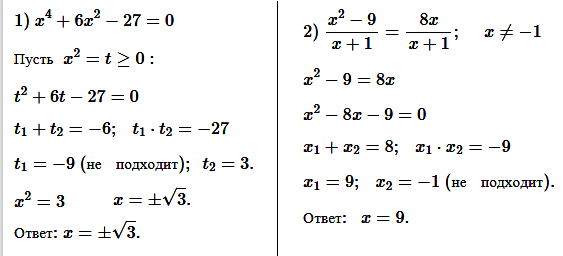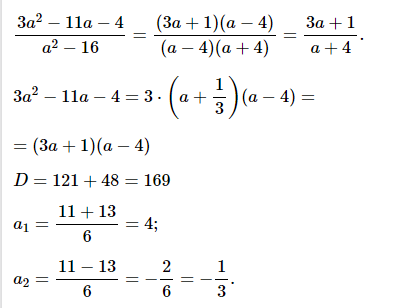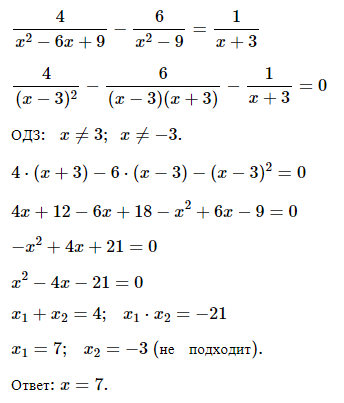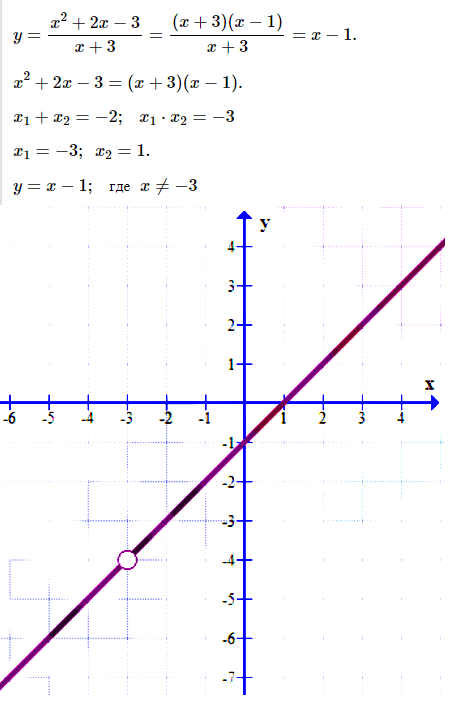Контрольная работа по теме квадратные и рациональные уравнения 8 класс

1. Решите уравнение

2. Решите уравнение

3. Два велосипедиста выезжают одновременно из пункта A и направляются в пункт B, удаленный от A на 90 км. Скорость первого велосипедиста на 1 км/ч больше скорости второго, поэтому первый велосипедист прибыл в B на 1 ч раньше второго. Какова скорость каждого велосипедиста?

4. Решите уравнение

5. Решите уравнение, если известно, что один из его корней равен 3.

Мерзляк 8 класс Контрольная 6 Варианты 3-4

Контрольная работа «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений» по алгебре в 8 классе с ответами для УМК Мерзляк, Полонский, Якир. Методическое пособие. Алгебра. Мерзляк 8 класс Контрольная 6 Варианты 3-4.

Алгебра 8 класс (УМК Мерзляк)
Контрольная работа № 6

по теме «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений»

Варианты 1 и 2 этой же контрольной работы № 6 смотрите тут:

Решения и Ответы на Вариант 3

№ 1. Разложите на множители квадратный трёхчлен: 1) x 2 – 2x – 24; 2) 3x 2 + 14x – 5.
ОТВЕТ:

№ 2. Решите уравнение: 1) x 4 + 2x 2 – 8 = 0; 2) (x 2 + 7x)/(x + 8) = 8/(x + 8).
ОТВЕТ:

№ 3. Сократите дробь 1) (2a 2 + 9a – 5)/(a 2 – 25).
ОТВЕТ:

№ 4. Решите уравнение 3/(x 2 + 4x + 4) + 4/(x 2 – 4) = 1/(x – 2).
ОТВЕТ:

№ 5. Теплоход прошёл 72 км против течения реки и 56 км по течению, затратив на путь против течения на 1 ч больше, чем на путь по течению. Найдите собственную скорость теплохода, если скорость течения реки составляет 2 км/ч.
ОТВЕТ: 26 км/ч.

№ 6. Постройте график функции у = (x 2 + 4 x – 5)/(x – 1).

Решения и Ответы на Вариант 4

№ 1. Разложите на множители квадратный трёхчлен: 1) x 2 + x – 30; 2) 2x 2 – 7x – 9.
ОТВЕТ:

№ 2. Решите уравнение: 1) x 4 + 6x 2 – 27 = 0; 2) (x 2 – 9)/(x + 1) = 8x/(x + 1).
ОТВЕТ:

№ 3. Сократите дробь (3a 2 – 11a – 4)/(a 2 – 16).
ОТВЕТ:

№ 4. Решите уравнение 4/(x 2 – 6x + 9) – 6/(x 2 – 9) = 1/(x + 3).
ОТВЕТ:

№ 5. Катер прошёл 64 км против течения реки и 38 км по течению, затратив на путь по течению на 1 ч меньше, чем на путь против течения. Найдите собственную скорость катера, если скорость течения реки составляет 3 км/ч.
ОТВЕТ: 22 км/ч.

№ 6. Постройте график функции у = (x 2 + 2 x – 3)/(x + 3).

Варианты 1 и 2 этой же контрольной работы № 6 смотрите тут:

Вы смотрели: Контрольную работу «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений» по алгебре в 8 классе с ответами для УМК Мерзляк, Полонский, Якир. Методическое пособие. Алгебра. Мерзляк 8 класс Контрольная 6 Варианты 3-4.

(с) Цитаты из пособия «Алгебра 8 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Мерзляк 8 класс Контрольная 6 Варианты 3-4: 1 комментарий

В задаче №5 четвертого варианта ошибка КР6 алгебра Мерзляк 8 класс

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Алгебра 8 Мордкович КР-6

Контрольная работа № 6 по алгебре в 8 классе (УМК Мордкович и др.) с ответами и решениями. Автор заданий: Л.А. Александрова. Алгебра 8 Мордкович КР-6. Задания контрольных работ представлены в учебных целях, а также для ознакомления и покупки учебного пособия. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий.

В контрольной работе проверяются знания учащихся после изучения следующих тем учебника:
§ 27. Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи).
§ 28. Частные случаи формулы корней квадратного уравнения.
§ 29. Теорема Виета. Разложение квадратного трехчлена на линейные множители.

Контрольная работа № 6
по алгебре в 8 классе (Мордкович)

КР-6. Вариант 1

№ 1. Определите число корней уравнения: а) 9х 2 + 12х + 4 = 0; б) 2х 2 + 3х – 11 = 0.

№ 2. Решите уравнение: а) х 2 – 14х + 33 = 0; б) –Зх 2 + 10х – 3 = 0; в) х 4 – 10х 2 + 9 = 0.

№ 3. Одна сторона прямоугольника на 9 см больше другой. Найдите стороны прямоугольника, если его площадь равна 112 см 2 .

№ 4. Решите уравнение 10/(25 – x 2 ) – 1/(5 + x) – x/(x – 5) = 0.

№ 5. При каких значениях параметра р уравнение 4х 2 + рх + 9 = 0 имеет один корень?

Решения и ОТВЕТЫ на КР-6 Вариант 1

Нажмите на спойлер, чтобы увидеть решения и ответы на все задания.

Контрольные работы по алгебре в 8 классе

2016 – 2017 учебный год.

Контрольные работы по алгебре в 8 классе.

Тема контрольной работы

Входная контрольная работа №1

Контрольная работа № 2

по теме «Квадратные корни»

Контрольная работа № 3«Преобразование выражений, содержащих квадратные корни»

Контрольная работа № 4

Контрольная работа № 5

«Уравнения, приводящиеся к квадратным»

Контрольная работа № 6

Контрольная работа № 7 «Неравенства»

Итоговая контрольная работа № 8

Предметные результаты уровн я подготовки учащихся 8 класса по алгебре

У чащиеся 8 класс а должны иметь представление :

о промежутках знакопостоянства функции;

о наибольшем и наименьшем значении функции на множестве.

У чащиеся 8 класс а должны знать:

определение иррационального числа;

определение действительного числа;

определение арифметического квадратного корня;

свойства арифметического квадратного корня;

виды тождественных преобразования выражений, содержащих квадратные корни;

определение квадратного уравнения;

виды квадратных уравнений;

определение приведенного квадратного уравнения;

определение биквадратного уравнения;

формулы корней квадратного уравнения;

теорему Виета и теорему, обратную теореме Виета;

определение квадратного трёхчлена;

определение корней квадратного трехчлена;

определение дробно-рационального неравенства;

сущность метода интервалов;

определение случайного события.

У чащиеся 8 класс а должны уметь:

строить график функции и устанавливать её свойства;

строить график функции у = ах 2 + п и устанавливать её свойства;

строить график функции у = а ( х – т ) 2 и устанавливать её свойства;

строить график функции у = а ( х – т ) 2 + п и устанавливать её свойства;

строить график функции у = ах 2 + bx + c ( а ≠ 0 ), и устанавливать её свойства;

выполнять тождественные преобразования выражений, содержащих квадратные корни;

решать квадратные уравнения;

использовать теорему Виета и теорему, обратную теореме Виета;

решать квадратные уравнения , содержащие переменную под знаком модуля;

решать уравнения, приводящиеся к квадратным уравнениям;

решать дробно- рациональные уравнения ;

решать рациональные уравнения , содержащие переменную под знаком модуля;

решать задачи с помощью составления квадратного и дробно-рационального уравнения;

находить корни квадратного трехчлена;

выполнять разложение квадратного трёхчлена на множители;

решать квадратные неравенства с помощью графика квадратичной функции и методом интервалов ;

решать рациональные неравенства методом интервалов.

У чащиеся 8 класс а должны владеть навыками:

использования справочных материалов, поиска определений, формул и других утверждений в учебной, методической и справочной литературе;

использования таблиц при нахождении значения квадратного корня ;

использования калькулятора для вычисления значений числовых выражений , содержащих квадратные корни ;

работы с компьютерными программами построения график а функции , квадратичной функци и ;

использования таблиц В. Брадиса для нахождения значений выражений , содержащих квадратные корни.

Контрольные работы по алгебре в 8 классе составлены в 4-6 вариантах различной сложности(Варианты1,2- самые простые, 3,4 – сложные варианты и 5,6- самые сложные). Каждая контрольная оценивается по критериям.

Входная контрольная работа №1

Повторение за курс 7 класса.

1.Найти значение выражения: (2 б)

2.Сократить дробь (2б) :

3.Разложить на множители (2б):

а) 5cb- 5с; б) pq – 4 p + 12 – 3 q .(2б)

4.Решить уравнения (4б) :

а)19 x – 8( x — 3) = 66 -3 x

5.Выполнить действия (5б):

1.Найти значение выражения (2 б) :

2.Сократить дробь (2 б) :

3.Разложить на множители (2б) :

a ) 10 n + 15 n 2 ; б) 5 y – 5 x + y 2 – xy .

4.Решить уравнения (4б) :

a ) 3 (5 x — 4) – 8 x = 4 x +9

Контрольная работа № 2 по теме «Квадратные корни»

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: при a 2 вариант .

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: при a В

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: + 2 а 3 при a вариант

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: + 2 а при a С

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: + 3 + при a 6 вариант

2.Найдите значение выражения:

3.Решите уравнение и неравенство

4.Упростите выражение: + 4 + при a Контрольная работа № 3

«Преобразование выражений, содержащих квадратные корни»

2.Сравните числовые выражения: А = и В =

4. Избавьтесь от иррациональности в знаменателе: .

5. Решите уравнение графическим способом: + 5х – 6 = 0

6.Укажите целые числа, удовлетворяющих неравенству: -≤ х вариант

2.Сравните числовые выражения: А = и В =

4. Избавьтесь от иррациональности в знаменателе: .

5. Решите уравнение графическим способом: ─ = 0

6.Укажите натуральные числа, удовлетворяющих неравенству: -6 ≤ х В

2.Сравните числовые выражения: А = и В =

4. Избавьтесь от иррациональности в знаменателе: .

5. Решите уравнение графическим способом: +4 x — 12 = 0

6.Укажите натуральные числа, удовлетворяющих неравенству: -≤ х вариант

2.Сравните числовые выражения: А = и В =

4. Избавьтесь от иррациональности в знаменателе: .

5. Решите уравнение графическим способом: = x – 2

6.Укажите целые числа, удовлетворяющих неравенству: -≤ х Контрольная работа № 4 «Квадратные уравнения»

У чащиеся 8 класс а должны знать:

определение квадратного уравнения;

виды квадратных уравнений;

определение приведенного квадратного уравнения;

определение биквадратного уравнения;

формулы корней квадратного уравнения;

теорему Виета и теорему, обратную теореме Виета;

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3.Найти сумму и произведение корней квадратного уравнения

4. Составьте квадратное уравнение, если его корни равны -1 и 8.

5.При каких значениях n уравнение х 2 + n х + 6 = 0 имеет один корень?

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3.Найти сумму и произведение корней квадратного уравнения

4. Составьте квадратное уравнение, если его корни равны -4 и 0.

5.При каких значениях n уравнение х 2 + n х + 11 = 0 имеет один корень?

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3.Найдите отрицательный корень уравнения -7х 2 +х +6 = 0

4.Один из корней уравнения х 2 + t х – 18 = 0 равен 9. Найдите второй корень и коэффициент t .

5. При каких значениях n уравнение 3х 2 + n х + 5 = 0 имеет один корень?

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3.Найдите положительный корень уравнения 30х 2 + 13х -1 = 0

4.Один из корней уравнения х 2 + t х +27 = 0 равен -9. Найдите второй корень и коэффициент t .

5. При каких значениях n уравнение 3х 2 + n х + 11 = 0 имеет один корень?

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3. Найдите второй корень данного уравнения , если один корень равен 4.

4.При каких значениях х значения выражений (х + 2) 2 – 28 и 20 + х – х 2 равны?

5. Составьте квадратное уравнение, если его корни равны .

6.Не решая уравнение 3х 2 – 5х – 2 = 0 вычислите значение выражения х 1 2 + х 2 2

1.Решить неполные квадратные уравнения:

2. Решить полные квадратные уравнения:

3. Найдите второй корень данного уравнения и коэффициент t , если один корень равен -7.

4.При каких значениях х значения выражений (х + 8) 2 – 40 и 2 — х –2х 2 равны?

5. Составьте квадратное уравнение, если его корни равны .

6.Не решая уравнение 6х 2 + 5х – 1 = 0 вычислите значение выражения +

Контрольная работа № 5

«Уравнения, приводящиеся к квадратным»

2. Найдите рациональный корень уравнения х 4 – 7х 2 +12 =0

3.Решая уравнение способом введения новой переменной, найдите целый корень.

4. Решите задачу. Из одного города в другой одновременно выехали два автомобиля. Скорость первого автомобиля была на 20 км/ ч больше, чем скорость второго автомобиля, поэтому он прибыл в город на 15 мин раньше. Найдите скоростькаждого автомобиля, если расстояние между городами равно 150 км.

2. Найдите иррациональный корень уравнения х 4 – 16х 2 +63 =0

3.Решая уравнение способом введения новой переменной, найдите целый корень.

4. Решите задачу. К намеченному сроку бригада должна была изготовить 240 деталей.Изготавливая ежедневно на 3 детали больше нормы, работу закончили на 4 дня раньше. Сколько деталей по плану должна была изготовить бригада за один день?

2. a ) Решите уравнения, используя метод введения новой переменной:

(2 z 2 +11 z ) 2 -23 (2 z 2 + 11 z ) +126 = 0

б) Решая уравнение способом введения новой переменной, найдите целый корень.

3. Решите задачу . Найдите меньшее из двух чисел, сумма которых равна 22, а сумма их квадратов – 250.

4. Решите задачу Один из катетов прямоугольного треугольника равен 2 а второй катет на 2 см меньше гипотенузы. Найдите второй катет и гипотенузу данного треугольника.

2. a ) Решите уравнения, используя метод введения новой переменной:

(2 х 2 + 3 ) 2 — 12 (2х 2 + 3) +11 = 0

б) Решая уравнение способом введения новой переменной, найдите целый корень.

3.Найдите большее из двух чисел, разность которых равна 4, а разность их квадратов – 104.

4. Гипотенуза прямоугольного треугольника равна 3 а разность катетов – 3 см.Найдите катеты и периметр прямоугольного треугольника.

а) (х 2 +3х +1) (х 2 +3х + 3) = -1

2 . Решите задачу. Мастер и ученик должны были выполнить работу к определенному сроку. Однако, когда была выполнена половина работы, ученик заболел, и мастер оставшись один, закончил работу с опозданием на 2 дня . За сколько дней мог бы выполнить работу каждый из них , работая по одному, если мастеру на это потребовалось бы на 5 дней меньше, чем ученику?

3. Составьте биквадратное уравнение, которое имеет корни х 1 = — , х 2 = , х 3 = -3, х 4 = 3.

а) (х 2 — 4х +1) (х 2 — 4х + 2) = 12

2 . Решите задачу. Пешеход прошел расстояние АВ за 3 часа. Возвращаясь, он первые 16 км шел с той же скоростью, а затем понизил на 1 км/ ч, и таким образом затратил на обратный путь на 4 мин больше, чем на путь из А в В. Найдите расстояние между А и В.

3. Составьте биквадратное уравнение, которое имеет корни х 1 = — , х 2 = , х 3 = -3, х 4 = 3.

Контрольная работа № 6

1. Для квадратичной функции у = 3х 2 + 5х -7 найдите у(-2).

2.При каких значениях аргумента значение функции у = — х 2 – 5х + 4 равно -2.

3.Найти координаты вершины параболы у = 2 (х — 3) 2 + 1

4. Напишите уравнение оси симметрии параболы у = х 2 + 6х – 3.

5.Запишите уравнение параболы у = х 2 + рх + q , вершина которой находится в точке А (-4; -9)

6.Постройте график функции у = (х — 2) 2 – 1

1. Для квадратичной функции у = -2х 2 + 7х -3 найдите у(-3).

2.При каких значениях аргумента значение функции у = х 2 – 4х – 3 равно -6.

3.Найти координаты вершины параболы у = -3 (х — 2) 2 – 4

4. Напишите уравнение оси симметрии параболы у = х 2 + 4х – 5.

5.Запишите уравнение параболы у = х 2 + рх + q , вершина которой находится в точке А (-3; -4)

6.Постройте график функции у = (х + 1) 2 – 2

Найдите нули функции у = 5х 2 – 4х – 1.

Сократите дробь и найдите ее значение при х = — 0,6

Используя график функции у = 3х 2 , постройте график функции у = 3 (х — 4) 2 + 2

Постройте график функции у = — х 2 – 9х – 16,25. Используя график функции, найдите промежутки возрастания и убывания, наибольшее значение функции.

Найдите нули функции у = 5х 2 – 7х + 2.

Сократите дробь и найдите ее значение при х = 2

Используя график функции у = -3х 2 , постройте график функции у = -3 (х + 2 ) 2 — 3

Постройте график функции у = х 2 – 7х + 11,25. Используя график функции, найдите промежутки возрастания и убывания, наименьшее значение функции.

Дана квадратичная функция у = 2х 2 + 4х – 6

1)Приведите ее к виду у = а(х — т) 2 + п.

2) Найдите координаты вершины параболы.

3) Вычислите значения х , при которых функция обращается в нуль.

4) Найдитенаибольшее и наименьшее значение функции.

5) Выясните при каких значениях х значение функции а) у > 0; б) у

6) На основании полученных результатов постройте график функции.

7) Выясните положение парабол относительно осей координат.

2. Е сли функция задана формулой f ( x ) = — x 2 + 3, то запишите формулу функции f (7 – x )

3.Сократите дробь и найдите ее значение при х = 2

4. Постройте график функции у =

1.Дана квадратичная функция у = -3х 2 + 12х – 5

1)Приведите ее к виду у = а(х — т) 2 + п.

2) Найдите координаты вершины параболы.

3)Вычислите значения х , при которых функция обращается в нуль.

4)Найдитенаибольшее и наименьшее значение функции.

5)Выясните при каких значениях х значение функции а) у > 0; б) у

6)На основании полученных результатов постройте график функции.

7)Выясните положение парабол относительно осей координат.

2. Е сли функция задана формулой f ( x ) = — x 2 + 3, то запишите формулу функции f (х – 2)

3.Сократите дробь и найдите ее значение при х = — 3

4. Постройте график функции у =

Контрольная работа № 7 «Неравенства»

Решите неравенство х 2 + х – 20

Найдите натуральные решения неравенства ≤ 0

Найдите целочисленные решения неравенства (х +7 )(х + 4) 2 (х -2) 0

При каких значениях х выражение имеет смысл?

1.Решите неравенство х 2 + 5х – 14 0

2.Найдите натуральные решения неравенства ≤ 0

4.Найдите целочисленные решения неравенства (х + 9) (х – 11) 2 (х -12) 0

5.При каких значениях х выражение имеет смысл?

1.Решите неравенство х 2 – 10х + 24 ≤ 0

2.Найдите натуральные решения неравенства ≤ 0

3.Решите неравенство а) ; б)

4.Найдите целочисленные решения неравенства (х – 3)(х – 4) 2 (х – 10) 0

5.При каких значениях х выражение имеет смысл?

1.Решите неравенство х 2 + 6х + 5 > 0

2.Найдите целые решения неравенства ≤ 0

3.Решите неравенство ; б) .

4.Найдите целочисленные решения неравенства (х +5 )(х + 1) 2 (х – 1) 0

5.При каких значениях х выражение имеет смысл?

Решите неравенство: а) (4х — 3) 2 + (3х – 7) 2 ≤ (5х + 1) 2 + 5х 2 + 4х – 123;

При каких значениях переменной имеет смысл выражение ?

Найдите наибольшее целое решение неравенства ≤ 0

Решите неравенство: 4

Решите неравенство: а) ( 5 х — 3) 2 + ( 12 х + 5 ) 2 ≤ ( 7 – 13 х ) 2 + 34 х 2 + 17 х + 4 1 0 ;

При каких значениях переменной имеет смысл выражение ?

Найдите наибольшее целое решение неравенства ≤ 1

Решите неравенство: ≤ 3

Итоговая контрольная работа № 8

Сократите дробь и найдите ее значение

2. Найдите значение выражения .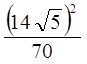

3. Упростите выражение:.

4. Запишите в стандартном виде число а) 3560; б) 0,0034.

5. Решите уравнение а); б)

6. Решите неравенство

7. Найдите координаты вершины параболы у = (х + 3) 2 – 4.

Решите уравнение методом введения новой переменной

Найдите наибольшее целое решение системы неравенств

Постройте график функции у = — х 2 + 3х +4. Укажите, при каких значениях аргумента функция принимает положительные значения.

Решите задачу. Велосипедист проехал с определенной скоростью путь 10 км от города до турбазы. Возвращаясь обратно, он снизил скорость на 5 км/ч. На весь путь туда и обратно потрачено 1 ч 10 мин. Найти его скорость от турбазы до города.

Найти значения а, при которых уравнение имеет два различных корня.

Сократите дробь и найдите ее значение

2. Найдите значение выражения .

3. Упростите выражение: .

4. Запишите в стандартном виде число а) 34500; б) 0,02349.

5. Решите уравнение а) ; б)

6. Решите неравенство

7. Найдите координаты вершины параболы у = (х – 2) 2 + 5.

Решить уравнение методом введения новой переменной

Найдите наибольшее целое решение системы неравенств

Постройте график функции у = -х 2 +5х+6. Укажите, при каких значениях аргумента функция принимает положительные значения.

Решите задачу. Мотоциклист проехал 40 км от пункта А до пункта В. Возвращаясь обратно со скоростью на 10 км/ч меньше первоначальной, он затратил на 20 мин больше. Найти первоначальную скорость мотоциклиста.

Найти значения а, при которых уравнение имеет два различных корня.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Наурзалинова Акмарал Асылбековна

26.01.2017

Алгебра

Контрольная работа

6709

2115

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

🎦 Видео