Контрольная работа по алгебре 8 класс квадратные и рациональные уравнения с ответами

Все задания даны в 4 вариантах. Подходит к учебнику «МГУ – в школе». Пособие используется для организации работы на уроке, номера могут задаваться в качестве домашних упражнений.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Преимущества дидактических материалов

Первая часть заданий нацелена на каждого ученика. Автор предлагает выполнить номера по образцу, что существенно облегчает решение. Здесь содержатся подробные объяснения, которые позволяют подготовиться к предстоящему уроку самостоятельно. В пособие включены задания со звездочкой. Они рекомендованы к использованию в классах с углубленным изучением математики. Номера в каждой работе даны в избытке. Автор предлагает учителям выбрать подходящие упражнения на свое усмотрение. Первый и второй варианты рассчитаны на учащихся общеобразовательных школ. Третьи и четвертые направлены на школьников математических гимназий и лицеев.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Как все выполнить самостоятельно

Хотите подготовиться к уроку и решить все задания на «отлично»? Вам поможет решебник к учебнику «Алгебра 8 класс Дидактические материалы Потапов, Шевкин Просвещение». Онлайн-пособие содержит решение и ответы на все номера. Изображения доступны в режиме онлайн. ГДЗ (готовые домашние задания) рекомендовано использовать для проверки знаний и правильности решения упражнений.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»

Контрольная работа содержит 4 варианта с подробным решением.

Просмотр содержимого документа
«Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»»

В а р и а н т 1

1. Решите уравнение:

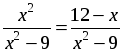
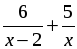
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

В а р и а н т 2

1. Решите уравнение:

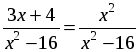
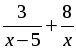
а) ; б) = 2.

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч.

В а р и а н т 3

1. Решите уравнение:

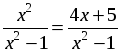
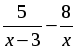
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?

В а р и а н т 4

1. Решите уравнение:

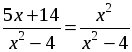
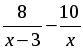
а) ; б) = 2.

2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?

Решение вариантов контрольной работы

В а р и а н т 1

1. а) 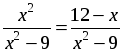. Общий знаменатель х 2 – 9.

По теореме, обратной теореме Виета, х₁ = 3; х₂ = –4.

Если х = 3, то х 2 – 9 = 0.

Если х = –4, то х 2 – 9 ≠ 0.

б) 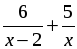= 3. Общий знаменатель х (х – 2).

D = (–17) 2 – 4 · 3 · 10 = 289 – 120 = 169, D 0, 2 корня.

x₁ = 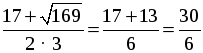= 5;

x₂ = .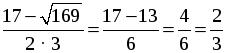

Если х = 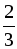, то х (х – 2) ≠ 0.

О т в е т: а) –4; б) 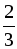; 5.

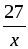
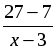
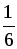
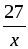
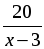
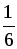
2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 10 мин ( часа) меньше, составим уравнение:

– = . Общий знаменатель 6х (х – 3).

D = (–45) 2 – 4 · 486 = 81, D 0, 2 корня.

x₁ = 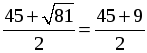= 27;

x₂ = 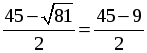= 18.

Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

О т в е т: 18 км/ч.

В а р и а н т 2

1. а) 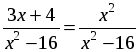. Общий знаменатель х 2 – 16.

По теореме, обратной теореме Виета х₁ = 4; х₂ = –1.

Если х = 4, то х 2 – 16 = 0.

Если х = – 1, то х 2 – 16 ≠ 0.

б) 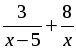= 2. Общий знаменатель х (х – 5).

D = (–21) 2 – 4 · 2 · 40 = 441 – 320 = 121, D 0, 2 корня.

x₁ = 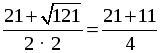= 8;

О т в е т: а) –1; б) 2,5; 8.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 3) км/ч, по течению – (х + 3) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

12х 2 + 36х + 5х 2 – 15х – 18х 2 + 162 = 0;

D = (–21) 2 – 4 · 162 = 441 + 648 = 1089, D 0, 2 корня.

Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи.

О т в е т: 27 км/ч.

В а р и а н т 3

1. а) 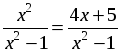. Общий знаменатель х 2 – 1.

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –1.

Если х = 5, то х 2 – 1 ≠ 0.

Если х = –1, то х 2 – 1 = 0.

б) 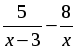= 3. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 4; х₂ = –2.

О т в е т: а) 5; б) –2; 4.

2. Пусть х км/ч – скорость, с которой велосипедист ехал из А в В, тогда (х + 4) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение:

– = 1. Общий знаменатель х (х + 4).

Ни один из корней не обращает знаменатель в нуль, но корень х = –12 не удовлетворяет условию задачи.

О т в е т: 16 км/ч.

В а р и а н т 4

1. а) 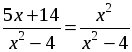. Общий знаменатель х 2 – 4.

По теореме, обратной теореме Виета, х₁ = 7; х₂ = –2.

Если х = 7, то х 2 – 4 ≠ 0.

Если х = –2, то х 2 – 4 = 0.

б) 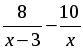= 2. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –3.

О т в е т: а) 7; б) –3; 5.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 2) км/ч, по течению – (х + 2) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

15х 2 + 30х + 6х 2 – 12х – 22х 2 + 88 = 0;

Ни один из корней не обращает знаменатель в нуль, но корень х = –4 не удовлетворяет условию задачи.

📹 Видео

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Алгебра 8 класс. Контрольная работа 6. По учебнику МакарычеваСкачать

Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Рациональные уравнения как модели реальных ситуаций. §24 алгебра 8 классСкачать

РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. §7 алгебра 8 классСкачать

КВАДРАТНЫЕ КОРНИ. Контрольная № 4. 8 класс.Скачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. СТЕПЕНЬ С ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ. ФУНКЦИЯ y=к/x. Контрольная №3 8 классСкачать

Алгебра 8 класс. Подготовка к контрольной работе по теме: "Рациональные дроби".Скачать

Итоговая контрольная работа по алгебре 8 классСкачать