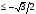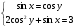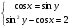Контрольная работа по алгебре 10 класс колмогоров тригонометрические уравнения и неравенства ответы

Контрольная работа по алгебре 10 класса «Тригонометрические уравнения и неравенства» представлены в четырех вариантах. Эти тексты можно использовать как самостоятельные работы, как задания для индивидуальной работы.

Данные тексты контрольных работ уместны не только при изучении темы, но и при итоговой повторении в конце учебного года, и про итоговом повторении в рамках подготовки к ЕГЭ.

Просмотр содержимого документа
«Контрольная работа «Тригонометрические уравнения и неравенства»»

КОНТРОЛЬНАЯ РАБОТА «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»

Вариант № 1 Вариант № 2

а) 2 sin x + 5 cos x = 0

б) 2 sin 2 x + 3 sinx cosx – 3 cos 2 x = 1

в) sin 2x + cos 2 x = 1

г) sin x = cos 3x

д) cos 5x + cos 3x + cos x = 0

а) 3 sin x – 7 cos x = 0

б) 4 sin 2 x + sinx cosx – cos 2 x = 1

в) sin 2x + sin 2 x = 1

г) cos x = sin 3x

д) sin 5x + sin 3x – sin 4x = 0

а) cos x

б) tg x

в) 2 cos 2 x + sin x – 1

а) sin x

в) 2 sin 2 x – 5 cosx + 1 0

4) Решить уравнения и неравенства. (Дополнительное задание )

а) sin x – 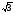cos x = 1

б) 3 + 2 sin 2x = tg x + ctg x

в) 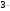(log₂sin x) 2 + log₂(1 – cos 2x) = 2

г) sin 2x + 2 sin x 0

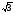
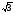
д) tg 2 x – 4 tg x + 0

е) lg log _cosx(7 – x) 0

5) Найти все значения р, при которых число х = 2 является корнем ур-ия.

Вариант № 3* Вариант № 4*( 2 ч. )

а) sin 2 x + sin 2 2x = sin 2 3x + sin 2 4x

б) 3 sin3x cos3x + 2 sin4x sin(п + x) = 3 sin5x cosx

в)

г) cos (2 sin x) =

д) sin 5 x – sin 4 x cosx = 2sin 3 x cos 2 x

е)

а) 1 – sin 4 x – 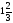cos 4 x = 0

б) 6 sin2x sin6x = 10 cos8x cos(п – x) + 3 cos 2 2x – 3 sin 2 2x

в)

г) sin (2 cos x) =

д) 3sin(x – п/4) = 2сos(x + п/3)

е)

2) Решить системы уравнений.

а) 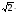(sin 2x – cos x) + 2 sin x 1 x

б) 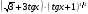0

в) 2 cos 2 (п/4 + x) – 3sin x cos x

г) 2 cos 2x – 9 sin x – 4 0 д)

а) 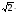(sin 2x + sin x) – 2 cos x

б) 0 в) 2sin 2 x + 5sin(п/4 + x)сos(п/4 + x) 0

г) 5 cos 2x + 22cos x + 9

4) При всех значениях параметра р решить.

а) б) cos 4x – 4 cos 4 x = р

5) При каких значениях параметра р уравнение tg (п/4 + х) + tg (п/4 – х) = 2р имеет решения?

6) При каких значениях параметра р уравнение не имеет корней?

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Контрольные работы по математике 10 класс (Колмогоров А.Н., Атанасян Л.С.)
материал по алгебре (10 класс) на тему

Контрольные работы по математике 10 класс (Колмогоров А.Н., Атанасян Л.С.)

Видео:Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Скачать:

Видео:Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

Предварительный просмотр:

Согласовано: заместитель директора

по УВР МКОУ «Покровская СОШ»

Косогор Евгения Николаевна

МКОУ «Покровская СОШ»

Иванова Светлана Анатольевна

Алгебра и начала математического анализа

Контрольная работа по теме:

Основные тригонометрические формулы»

1. Найдите значение выражения:

а) 2cos 60º — 3 tg45 º + sin 270 º;

б) 4sin 210º — ctg 135 º.

1. Сравните с нулем значение выражения , если 90º
2. Найдите значения sin и ctg , зная, что cos и π .

1. Упростите выражение sin
2. Расположите в порядке возрастания числа sin 3 π ; соs 0,2; cos 4,2.

«5» — верно выполнены все задания;

«4» — верно выполнены 4 задания;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Тригонометрические функции числового аргумента»

1. Упростите выражение
2. Постройте график функции y = cos x. Какая из точек М принадлежит этому графику?

1. Дана функция у = 1 – 2sin x. Найдите:

а) область определения и область значений этой функции;

б) все значения х, при которых у = — 1.

«5» — верно выполнены все задания;

«4» — выполнены 4 задания, но есть ошибка;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Основные свойства функций»

1. Изобразите схематически график функции и перечислите ее основные свойства:

а) у = (х – 2) 4 ; б) у = 0,5sinx + 2.

1. Докажите, что функция f(x) = 2х 3 – tg x является нечетной.

1. Расположите в порядке убывания числа cos(-1,1); cos 0,2; cos 2,9; cos 4,2.

«5» — верно выполнены все задания;

«4» — выполнены 3 задания, но есть ошибка;

«3» — верно выполнены 2 задания.

Контрольная работа по теме:

«Решение тригонометрических уравнений и неравенств»

б) cos 2 x + 3sinx – 3 = 0;

в) 2sin 2 x – sin2x = cos2x.

1. Решите неравенство sin x ≤

1. Решите уравнение cos 3x + cos х = 0 и найдите все его корни, принадлежащие промежутку

«5» — верно выполнены все задания;

«4» — выполнены 3 задания, но есть ошибка;

«3» — верно выполнены 2 задания.

Контрольная работа по теме: «Производная»

1. Найдите производную функции:

а) , если f(x) = x cosx;

б) , если f(x) = (3x + 4) 5 .

1. Найдите все значения х, при которых = 0, если f(x) = cos 2x + .
2. Найдите все значения х, при которых ≤ 0, если f(x) = 6х – х 3 .

«5» — верно выполнены все задания;

«4» — верно выполнены 3 задания;

«3» — верно выполнены 2 задания.

Контрольная работ по теме:

«Применение производной к исследованию функции»

1. Решите неравенство х – ≥ 0.
2. К графику функции f(x) = х 5 – 6х 3 проведена касательная через его точку с абсциссой х 0 =1. Вычислите тангенс угла наклона этой касательной к оси абсцисс.
3. Прямолинейное движение точки описывается законом x(t) = t 4 – 2t 2 . Найдите ее скорость и ускорение в момент времени t = 3. (Время измеряется в секундах, перемещение – в метрах.)

1. Найдите наибольшее и наименьшее значения функции f(x) = х 3 – 3х 2 + 4 на промежутке [0; 4].
2. Представьте число 42 в виде суммы трех положительных слагаемых таким образом, чтобы их произведение было наибольшим, а два слагаемых были пропорциональны числам 2 и 3.

«5» — верно выполнены все задания;

«4» — верно выполнены 4 задания;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Параллельность прямых и плоскостей» (20 мин)

1. Основание АD трапеции ABCD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках E и F соответственно.

а) Каково взаимное расположение прямых EF и AB ?

б) Чему равен угол между прямыми EF и AB , если ? Ответ обоснуйте.

1. Дан пространственный четырехугольник ABCD , в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. Выполните рисунок к задаче.

1. Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC . Точка P – середина стороны AD , а K – середина стороны DC .

а) Каково взаимное положение прямых PK и AB ?

б) Чему равен угол между прямыми PK и AB , если и ? Ответ обоснуйте.

1. Дан пространственный четырехугольник ABCD , M и N – середины сторон AB и BC соответственно, . Выполните рисунок к задаче.

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

«Параллельность прямых и плоскостей»

1. Прямые а и b лежат в параллельных плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

1. Через точку О, лежащую между параллельными плоскостями и , проведены прямые l и m . Прямая l пересекает плоскости и в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 2 В 2 , если , .

1. Прямые а и b лежат в пересекающихся плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

1. Через точку О, не лежащую между параллельными плоскостями и , проведены прямые l и m . Прямая l пересекает плоскости и в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 1 В 1 , если , .

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

«Перпендикулярность прямых и плоскостей»

1. Диагональ куба равна 6 см. Найдите:

б) косинус угла между диагональю куба и плоскостью одной из его граней.

1. Сторона AB ромба ABCD равна a , один из углов равен 60°. Через сторону AB проведена плоскость на расстоянии 0,5 a от точки D .

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла DABM , .

1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна см, а его измерения относятся как 1 : 1 : 2. Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

1. Сторона квадрата ABCD равна a . Через сторону AD проведена плоскость на расстоянии 0,5 a от точки B .

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла BADM , .

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

1. Основанием пирамиды DABC является правильный треугольник ABC , сторона которого равна a . Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью ABC угол 30 ° . Найдите площадь боковой поверхности пирамиды.

1. Основание прямого параллелепипеда является ромб ABCD , сторона которого равна a и угол равен 60 ° . Плоскость AD 1 C 1 составляет с плоскостью основания угол 60 ° .

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда.

1. Основанием пирамиды MABCD является квадрат ABCD , ребро MD перпендикулярно к плоскости основания, . Найдите площадь поверхности пирамиды.

1. Основание прямого параллелепипеда является параллелограмм ABCD , стороны которого равны и 2 a , острый угол равен 45 ° . Высота параллелепипеда равна меньшей высоте параллелограмма.

а) меньшую высоту параллелограмма;

б) угол между плоскостью и плоскостью основания;

в) площадь боковой поверхности параллелепипеда.

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Контрольные работы «Тригонометрические уравнения и неравенства. Производная»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Контрольные работы к учебнику «Алгебра и начала

математического анализа,10» С.М. Никольского и др.

Контрольная работа №1

Тригонометрические уравнения и неравенства

а) cos x =-1; б) sinx = ; в) ctgx =- .

2. а) sin 2 x + sinx -2=0; б) 3 sin 2 x — cosx +1=0.

3. a) sinx- cosx=0; б ) 3sin 2 x+2sinx cosx+cos 2 x=0.

4. а) sin x =- 0,5; б) cos x = ; в) tgx =-3.

5 a) sinx+ cosx=1; б ) 2cos 2 x+sin4x=1.

6 Решите неравенство :

а) Sin x cos x >0,5; в) tgx ≤-3.

г ) 2cos 2 x+sin x >2

7) sin 2x=cos 4 -sin 4

8) =6cos x-2

9) cos 9x-cos 7x+cos 3x-cos x=0

10) +3 cos 2 x =1-2 cos x

а) sinx =-1; б) cosx = ; в) tgx =- .

2. а ) cos 2 x-cos x-2=0; б ) 3cos 2 x-2sinx+2=0.

3. a) sinx+ cosx=0; б ) 3sin 2 x-2 sinx cosx +cos 2 x=0.

4. а) cos x =- 0,5; б) sin x =; в) tg x =2

5 a) sinx- cosx=1; б ) 2cos 2 x-sin4x=1.

6 Решите неравенство

а ) Sin x>0,5; б )cos x

г ) 2sin 2 x- cos x >2

7) ctg x-sinx=2sin 2

8) =6sinx-1

9) 8-4sin 2 x=sin2x ctgx — 9cosx

10) sin x sin3x+sin4x sin8x=0

а) cos x =1; б) sinx =; в) ctgx =-.

2. а ) 2 sin 2 x+sinx-1=0; б ) 3cos 2 x-sinx+1=0.

3. a) sinx- cosx=0; б ) sin 2 x+2 sinx cosx+3cos 2 x=0.

4. а) sin x = -0,6; б) cos x =; в) tgx =-4

5 a) sinx+ cosx=-1; б ) 2cos 4x+cos 2 x=1.

6 Решите неравенство:

а ) Sin x>-0,5; б )cos x

г ) 4cos 2 x- (2-2)sin x > 4-

7) sin 2x=cos 4 -sin 4

8) =+cos x

9) cos 9x-cos 7x+cos 3x-cos x=0

10) +3cos 2 x=1-2cos x

а) sin x =1; б) cosx =; в) tgx =-.

2. а ) 2 cos 2 x-cosx-1=0; б ) 3sin 2 x-2cosx+2=0.

3. a) sinx+ cosx=0; б ) sin 2 x-2 sinx cosx+3cos 2 x=0.

4. а) cos x = -0,7 б) cos x =; в) tg x =5

5 a) sinx- cosx=-1; б ) cos 4x-sin 2 x=1.

6 Решите неравенство:

а ) Sin x б )cos x>-0,5; tgx ≤ 2

г ) 4 sin 2 x+ (2-2)cos x > 4-

7) ctg x-sinx=2sin 2

8) =6sinx-1

9) 8-4sin 2 x=sin2x ctgx — 9cosx

10) sin x sin3x+sin4x sin8x=0

Контрольная работа №2

а) ƒ(х)=6х 4 +5х 3 +3х 2 +3, х ₀ =1; б) ƒ(х)=х со s x , х ₀ =

2. Найдите ƒ'(х), если:

а) ƒ(х)=; б) ƒ(х)=7 7 3 ; в) ƒ(х)= log ₅ x ; г) ƒ(х) =

3.Вычислите значение производной функции у=с tg 3 x в точке х ₀ =

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 +3х 2 -9х-13 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)=— 6 3 4 ; б) ƒ(х)=e 3х+2 ; в) ƒ(х)=х√х 2 -3х+4

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=17+24х-4t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

8. Найдите производную функции

а) у=х 3 со s б) y = log ₈ (9 x +7)· arctg 2 3 x 4

в) y=cos —

а) ƒ(х)=3х 5 -12х 2 +6х+3, х ₀ =1; б) ƒ(х)=х sinx х ₀ =

2. Найдите ƒ'(х), если:

а) ƒ(х)=; б) ƒ(х)=5 5 3 ; в) ƒ(х)=5 x ; г) ƒ(х) =

3.Вычислите значение производной функции у= tg 4 x в точке х ₀ =-

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 -6х 2 +9х-11 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)=— 3 3 4 ; б) ƒ(х)= ln (3+2 x ); в) ƒ(х)=х√х 2 +2х+3

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=13+10t-5t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

ƒ(х)= ln

8. Найдите производную функции

а) у=х 2 со s б) y = log ₃ (9 x +7)· arcctg 2 x 3

в) y=sin —

а) ƒ(х)=-5х 4 +4х 3 +6х 2 -2 x +3, х ₀ =1; б) ƒ(х)=х tgx х ₀ =

2. Найдите ƒ'(х), если:

а) ƒ(х)=; б) ƒ(х)=5 5 4 ; в) ƒ(х)=10 x ; г) ƒ(х) =

3.Вычислите значение производной функции у= cos 3 x в точке х ₀ =-

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 -4х 2 +5х-17 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)=— 12 3 5 ; б) ƒ(х)= lg (4-3 x ); в) ƒ(х)=4х√3х 2 -2х+1

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=23+20t-5t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

ƒ(х)= ln

8. Найдите производную функции

а) у=х 3 со s б) y = log ₈ (9 x +7)· arctg 2 3 x 4

в) y=cos —

а) ƒ(х)=5х 3 -4х 4 +2х 2 -2 x +5, х ₀ =1; б) ƒ(х)=х ctgx х ₀ =

2. Найдите ƒ'(х), если:

а) ƒ(х)=; б) ƒ(х)=7 7 6 ; в) ƒ(х)= lg x ; г) ƒ(х) =

3.Вычислите значение производной функции у= sin 2 x в точке х ₀ =

4. Найдите все значения х, при каждом из которых производная функции

а) ƒ(х)= х 3 +2х 2 -7х-13 равна нулю.

5. Найдите ƒ'(х), если:

а) ƒ(х)=— 6 3 5 ; б) ƒ(х)=10 4 x -3 ); в) ƒ(х)=4х√4х 2 -2х+1

6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=27+24t-2t 2 .Найдите момент времени t, когда точка остановится.

7. Найдите производную функции

8. Найдите производную функции

а) у=х 2 со s б) y = log ₃ (9 x +7)· arcctg 2 x 3

в) y=sin —

Краткое описание документа:

Методические материалы к контрольным работам по математике 10 класса «Тригонометрические уравнения и неравенства. Производная» представлены в четырех вариантах. Эти тексты можно использовать как самостоятельные работы, как задания для индивидуальной работы. Данные тексты контрольных работ уместны не только при изучении темы, но и при итоговой повторении в конце учебного года, и про итоговом повторении в рамках подготовки к ЕГЭ.

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 700 человек из 76 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 860 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 47 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Алгебра 10 класс // Логарифмы // Контрольная работа // Решение, ответы // К учебнику АлимоваСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 846 091 материал в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 28.04.2015
• 1368
• 11

• 28.04.2015
• 708
• 0

• 28.04.2015
• 13506
• 34

• 28.04.2015
• 1206
• 0

• 28.04.2015
• 2346
• 0

• 28.04.2015
• 8101
• 161

• 28.04.2015
• 1742
• 1

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 28.04.2015 37545
• DOCX 162.5 кбайт
• 360 скачиваний
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Максимович Надежда Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 5 месяцев
• Подписчики: 0
• Всего просмотров: 122389
• Всего материалов: 42

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Роспотребнадзор сообщил об опасности размещения вышек сотовой связи на территории школ

Время чтения: 1 минута

Путин объявил 2022-2031 годы Десятилетием науки и технологий

Время чтения: 1 минута

В России выросло число детей с ОВЗ, поступающих в колледжи

Время чтения: 1 минута

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔥 Видео

10 класс Контрольная по тригонометрииСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Алгебра 10 класс (Урок№48 - Тригонометрические уравнения с параметрами.)Скачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Подробные решения упражнений из учебника Колмогорова для 10-11 классов #1 Тригонометрические функцииСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Алгебра 10 класс (Урок№52 - Решение задач итоговой аттестации.)Скачать