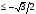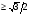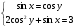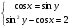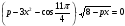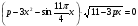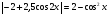Контрольная работа по алгебре 10 класс колмогоров тригонометрические уравнения и неравенства

Контрольная работа по алгебре 10 класса «Тригонометрические уравнения и неравенства» представлены в четырех вариантах. Эти тексты можно использовать как самостоятельные работы, как задания для индивидуальной работы.

Данные тексты контрольных работ уместны не только при изучении темы, но и при итоговой повторении в конце учебного года, и про итоговом повторении в рамках подготовки к ЕГЭ.

Просмотр содержимого документа
«Контрольная работа «Тригонометрические уравнения и неравенства»»

КОНТРОЛЬНАЯ РАБОТА «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»

Вариант № 1 Вариант № 2

а) 2 sin x + 5 cos x = 0

б) 2 sin 2 x + 3 sinx cosx – 3 cos 2 x = 1

в) sin 2x + cos 2 x = 1

г) sin x = cos 3x

д) cos 5x + cos 3x + cos x = 0

а) 3 sin x – 7 cos x = 0

б) 4 sin 2 x + sinx cosx – cos 2 x = 1

в) sin 2x + sin 2 x = 1

г) cos x = sin 3x

д) sin 5x + sin 3x – sin 4x = 0

а) cos x

б) tg x

в) 2 cos 2 x + sin x – 1

а) sin x

в) 2 sin 2 x – 5 cosx + 1 0

4) Решить уравнения и неравенства. (Дополнительное задание )

а) sin x – 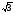cos x = 1

б) 3 + 2 sin 2x = tg x + ctg x

в) 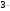(log₂sin x) 2 + log₂(1 – cos 2x) = 2

г) sin 2x + 2 sin x 0

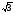
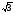
д) tg 2 x – 4 tg x + 0

е) lg log _cosx(7 – x) 0

5) Найти все значения р, при которых число х = 2 является корнем ур-ия.

Вариант № 3* Вариант № 4*( 2 ч. )

а) sin 2 x + sin 2 2x = sin 2 3x + sin 2 4x

б) 3 sin3x cos3x + 2 sin4x sin(п + x) = 3 sin5x cosx

в)

г) cos (2 sin x) =

д) sin 5 x – sin 4 x cosx = 2sin 3 x cos 2 x

е)

а) 1 – sin 4 x – 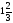cos 4 x = 0

б) 6 sin2x sin6x = 10 cos8x cos(п – x) + 3 cos 2 2x – 3 sin 2 2x

в)

г) sin (2 cos x) =

д) 3sin(x – п/4) = 2сos(x + п/3)

е)

2) Решить системы уравнений.

а) 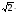(sin 2x – cos x) + 2 sin x 1 x

б) 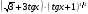0

в) 2 cos 2 (п/4 + x) – 3sin x cos x

г) 2 cos 2x – 9 sin x – 4 0 д)

а) 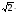(sin 2x + sin x) – 2 cos x

б) 0 в) 2sin 2 x + 5sin(п/4 + x)сos(п/4 + x) 0

г) 5 cos 2x + 22cos x + 9

4) При всех значениях параметра р решить.

а) б) cos 4x – 4 cos 4 x = р

5) При каких значениях параметра р уравнение tg (п/4 + х) + tg (п/4 – х) = 2р имеет решения?

6) При каких значениях параметра р уравнение не имеет корней?

Видео:Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

Контрольная работа по АиНА в 10 классе по теме» Тригонометрические уравнения, неравенства и их системы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Контрольная работа по АиНА в 10 классе по теме: « Тригонометрические уравнения и неравенства, и их системы»

1. Решите уравнения:

1) ; 2) ;

3) ; 4) ;

5) ; 6)

2.Решите систему уравнений :

1) 2) 3)

4. Решите систему неравенств:

1) 2) 3)

Видео:Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Контрольные работы по математике 10 класс (Колмогоров А.Н., Атанасян Л.С.)
материал по алгебре (10 класс) на тему

Контрольные работы по математике 10 класс (Колмогоров А.Н., Атанасян Л.С.)

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Скачать:

Видео:Тригонометрия в ЕГЭ может быть простойСкачать

Предварительный просмотр:

Согласовано: заместитель директора

по УВР МКОУ «Покровская СОШ»

Косогор Евгения Николаевна

МКОУ «Покровская СОШ»

Иванова Светлана Анатольевна

Алгебра и начала математического анализа

Контрольная работа по теме:

Основные тригонометрические формулы»

1. Найдите значение выражения:

а) 2cos 60º — 3 tg45 º + sin 270 º;

б) 4sin 210º — ctg 135 º.

1. Сравните с нулем значение выражения , если 90º
2. Найдите значения sin и ctg , зная, что cos и π .

1. Упростите выражение sin
2. Расположите в порядке возрастания числа sin 3 π ; соs 0,2; cos 4,2.

«5» — верно выполнены все задания;

«4» — верно выполнены 4 задания;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Тригонометрические функции числового аргумента»

1. Упростите выражение
2. Постройте график функции y = cos x. Какая из точек М принадлежит этому графику?

1. Дана функция у = 1 – 2sin x. Найдите:

а) область определения и область значений этой функции;

б) все значения х, при которых у = — 1.

«5» — верно выполнены все задания;

«4» — выполнены 4 задания, но есть ошибка;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Основные свойства функций»

1. Изобразите схематически график функции и перечислите ее основные свойства:

а) у = (х – 2) 4 ; б) у = 0,5sinx + 2.

1. Докажите, что функция f(x) = 2х 3 – tg x является нечетной.

1. Расположите в порядке убывания числа cos(-1,1); cos 0,2; cos 2,9; cos 4,2.

«5» — верно выполнены все задания;

«4» — выполнены 3 задания, но есть ошибка;

«3» — верно выполнены 2 задания.

Контрольная работа по теме:

«Решение тригонометрических уравнений и неравенств»

б) cos 2 x + 3sinx – 3 = 0;

в) 2sin 2 x – sin2x = cos2x.

1. Решите неравенство sin x ≤

1. Решите уравнение cos 3x + cos х = 0 и найдите все его корни, принадлежащие промежутку

«5» — верно выполнены все задания;

«4» — выполнены 3 задания, но есть ошибка;

«3» — верно выполнены 2 задания.

Контрольная работа по теме: «Производная»

1. Найдите производную функции:

а) , если f(x) = x cosx;

б) , если f(x) = (3x + 4) 5 .

1. Найдите все значения х, при которых = 0, если f(x) = cos 2x + .
2. Найдите все значения х, при которых ≤ 0, если f(x) = 6х – х 3 .

«5» — верно выполнены все задания;

«4» — верно выполнены 3 задания;

«3» — верно выполнены 2 задания.

Контрольная работ по теме:

«Применение производной к исследованию функции»

1. Решите неравенство х – ≥ 0.
2. К графику функции f(x) = х 5 – 6х 3 проведена касательная через его точку с абсциссой х 0 =1. Вычислите тангенс угла наклона этой касательной к оси абсцисс.
3. Прямолинейное движение точки описывается законом x(t) = t 4 – 2t 2 . Найдите ее скорость и ускорение в момент времени t = 3. (Время измеряется в секундах, перемещение – в метрах.)

1. Найдите наибольшее и наименьшее значения функции f(x) = х 3 – 3х 2 + 4 на промежутке [0; 4].
2. Представьте число 42 в виде суммы трех положительных слагаемых таким образом, чтобы их произведение было наибольшим, а два слагаемых были пропорциональны числам 2 и 3.

«5» — верно выполнены все задания;

«4» — верно выполнены 4 задания;

«3» — верно выполнены 3 задания.

Контрольная работа по теме:

«Параллельность прямых и плоскостей» (20 мин)

1. Основание АD трапеции ABCD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках E и F соответственно.

а) Каково взаимное расположение прямых EF и AB ?

б) Чему равен угол между прямыми EF и AB , если ? Ответ обоснуйте.

1. Дан пространственный четырехугольник ABCD , в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. Выполните рисунок к задаче.

1. Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC . Точка P – середина стороны AD , а K – середина стороны DC .

а) Каково взаимное положение прямых PK и AB ?

б) Чему равен угол между прямыми PK и AB , если и ? Ответ обоснуйте.

1. Дан пространственный четырехугольник ABCD , M и N – середины сторон AB и BC соответственно, . Выполните рисунок к задаче.

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

«Параллельность прямых и плоскостей»

1. Прямые а и b лежат в параллельных плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

1. Через точку О, лежащую между параллельными плоскостями и , проведены прямые l и m . Прямая l пересекает плоскости и в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 2 В 2 , если , .

1. Прямые а и b лежат в пересекающихся плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

1. Через точку О, не лежащую между параллельными плоскостями и , проведены прямые l и m . Прямая l пересекает плоскости и в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 1 В 1 , если , .

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

«Перпендикулярность прямых и плоскостей»

1. Диагональ куба равна 6 см. Найдите:

б) косинус угла между диагональю куба и плоскостью одной из его граней.

1. Сторона AB ромба ABCD равна a , один из углов равен 60°. Через сторону AB проведена плоскость на расстоянии 0,5 a от точки D .

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла DABM , .

1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна см, а его измерения относятся как 1 : 1 : 2. Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

1. Сторона квадрата ABCD равна a . Через сторону AD проведена плоскость на расстоянии 0,5 a от точки B .

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла BADM , .

«5» — верно выполнены все задания;

«4» — выполнены 2 задания, но есть ошибка;

«3» — верно выполнено 1 задание.

Контрольная работа по теме:

1. Основанием пирамиды DABC является правильный треугольник ABC , сторона которого равна a . Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью ABC угол 30 ° . Найдите площадь боковой поверхности пирамиды.

1. Основание прямого параллелепипеда является ромб ABCD , сторона которого равна a и угол равен 60 ° . Плоскость AD 1 C 1 составляет с плоскостью основания угол 60 ° .

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда.

1. Основанием пирамиды MABCD является квадрат ABCD , ребро MD перпендикулярно к плоскости основания, . Найдите площадь поверхности пирамиды.

1. Основание прямого параллелепипеда является параллелограмм ABCD , стороны которого равны и 2 a , острый угол равен 45 ° . Высота параллелепипеда равна меньшей высоте параллелограмма.

а) меньшую высоту параллелограмма;

б) угол между плоскостью и плоскостью основания;

в) площадь боковой поверхности параллелепипеда.

💡 Видео

10 класс Контрольная по тригонометрииСкачать

Контрольная работа 1Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Подробные решения упражнений из учебника Колмогорова для 10-11 классов #1 Тригонометрические функцииСкачать

Математика 10 Класс (Алгебра и Геометрия)Скачать

Алгебра 10 класс (Урок№48 - Тригонометрические уравнения с параметрами.)Скачать