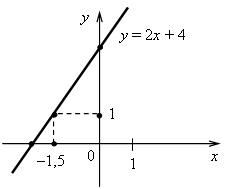Просмотр содержимого документа
«Контрольная работа «Линейные уравнения»»
1. Решите уравнение:
а) 11х – 7 = 6х + 18; б) 3(5 – 3х) +3 = -6х + 4
2. В одном мешке было в 3 раза больше муки, чем в другом. Когда из первого мешка взяли 8 кг. муки, а во второй добавили 4 кг., то в мешках муки стало поровну. Сколько килограммов муки было в каждом мешке сначала?
3. Решите уравнение:
а) ( 12у +18)(1,6 – 0,2у) = 0; б) 0,1(2х-3)=6-4(1,6-0,3х)
4. В первый магазин завезли 100 кг конфет, а во второй – 240 кг. Первый магазин продавал ежедневно по 12 кг конфет, а второй – по 46 кг. Через сколько дней во втором магазине останется в 4 раза меньше конфет, чем в первом?
5. При каком значении а уравнение (а + 3) х = 12:
а) имеет корень, равный 6; б) не имеет корней?
1. Решите уравнение:
а) 9х – 8 = 4х + 12; б) 9 – 7(х+3) = 5 – 4х.
2. В первом ящике было в 4 раз больше яблок, чем во втором. Когда из первого ящика взяли 7 кг яблок, а во второй добавили 5 кг, то в ящиках яблок стало поровну. Сколько килограммов яблок было в каждом ящике сначала?
3. Решите уравнение:
а) (8у – 12)(2,1 + 0,3у) = 0; б) 0,4(0,5х-2)=5,5-0,3(3х-1)
4. В футбольной секции первоначально занималось в 3 раз больше учеников, чем в баскетбольной. Когда в футбольную секцию поступило ещё 9 учеников, а в баскетбольную – 33 ученика, то в секциях учеников стало поровну. Сколько учеников было в каждой секции сначала?
5. При каком значении а уравнение (а — 2)х = 35:
а) имеет корень, равный 5; б) не имеет корней?
Видео:Линейные уравнения. Линейные неравенства. Линейная функция. Контрольная работа №3 по алгебре.7 классСкачать

Контрольная работа № 3 по теме: «линейная функция».
Цели: проверить знания, умение решать задачи и навыки учащихся по теме «Линейная функция»; развивать логическое мышление учащихся; воспитывать внимание.
Оборудование: карточки с вариантами
Просмотр содержимого документа
«Контрольная работа № 3 по теме: «линейная функция».»
КОНТРОЛЬНАЯ РАБОТА № 3 по теме: «Линейная функция».
Цели: проверить знания, умение решать задачи и навыки учащихся по теме «Линейная функция»; развивать логическое мышление учащихся; воспитывать внимание.
Оборудование: карточки с вариантами.
I. Организация учащихся на выполнение работы.
II. Выполнение работы по четырем вариантам.
1. Функция задана формулой у = 6х + 19. Определите:
а) значение у, если х = 1;
б) значение х, при котором у = 1;
в) проходит ли график функции через точку А (–2; 7).
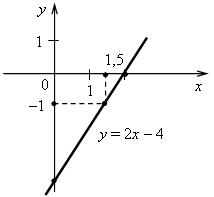
2. а) Постройте график функции у = 2х – 4.
б) Укажите с помощью графика, чему равно значение у при х = 0.
3. В одной и той же системе координат постройте графики функций:
4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
1. Функция задана формулой у = 4х – 30. Определите:
а) значение у, если х = 10;
б) значение х, при котором у = –6;
в) проходит ли график функции через точку В (7; –3).
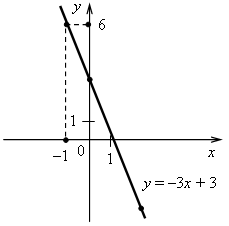
2. а) Постройте график функции у = –3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
3. В одной и той же системе координат постройте графики функций:
4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат.
1. Функция задана формулой у = 5х + 18. Определите:
а) значение у, если х = 1;
б) значение х, при котором у = 3;
в) проходит ли график функции через точку С (–6; –12).
2. а) Постройте график функции у = 2х + 4.
б) Укажите с помощью графика, чему равно значение у при х = 0.
3. В одной и той же системе координат постройте графики функций:
4. Найдите координаты точки пересечения графиков функций
у = –14х + 32 и у = 26х – 8.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.
1. Функция задана формулой у = 2х – 15. Определите:
а) значение у, если х = 10;
б) значение х, при котором у = –5;
в) проходит ли график функции через точку K (10; –5).
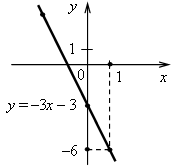
2. а) Постройте график функции у = –3х – 3.
б) Укажите с помощью графика, при каком значении х значение у равно –6.
3. В одной и той же системе координат постройте график функций:
4. Найдите координаты точки пересечения графиков функций
у = –10х – 9 и у = –24х + 19.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат.
Рекомендации по оцениванию.
Задания 1–3 относятся к базовому уровню знаний по теме. Верное выполнение любых трех заданий оценивается отметкой «3». Для получения отметки «5» необходимо выполнить верно все пять заданий.
Решение заданий контрольной работы
а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22;
б) если у = 1, то 6х + 19 = 1;
7 = 7 – верно, значит, график функции проходит через точку
А (–2; 7).
Ответ: а) 22; б) –3; в) проходит.
Построим две точки, принадлежащие графику.
Если х = 0, то у = 2 · 0 – 4 = –4;
если х = 2, то у = 2 · 2 – 4 = 0.
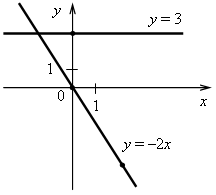
3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4).
б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х.
4. Решим уравнение:
х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты:
если х = 1, то у = 47 · 1 – 37 = 10.
Точка пересечения имеет координаты (1; 10).
5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х.
а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40;
б) если у = –6, то 4х – 30 = –6;
–3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3).
Ответ: а) –40; б) 6; в) не проходит.
Построим две точки, принадлежащие графику.
Если х = 0, то у = –3 · 0 + 3 = 3;
если х = 2, то у = –3 · 2 + 3 = –3;
б) Если у = 6, то х = –1.
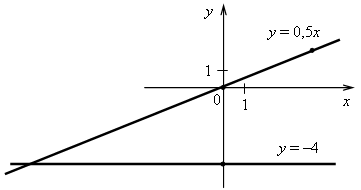
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.
4. Решим уравнение:
х = 3, значит, абсцисса точки пересечения графиков функций равна 3.
Найдем соответствующее значение ординаты:
если х = 3, то у = –38 · 3 + 15 = –99.
Точка пересечения имеет координаты (3; –99).
5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х.
а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20;
б) если у = 3, то 5х + 18 = 3;
–12 = –12 – верно, значит, график функции проходит через точку
С (–6; –12).
Ответ: а) 20; б) –3; в) проходит.
Построим две точки, принадлежащие графику.
Если х = 0, то у = 2 · 0 + 4 = 4;
если х = –2, то 2 · (–2) + 4 = 0.
б) Если х = –1,5, то у = 1.
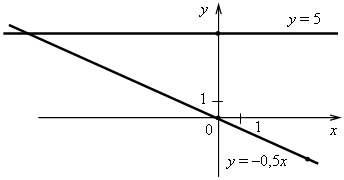
3. а) у = –0,5х. Графиком является прямая, проходящая через начало координат и точку (4; –2).
б) у = 5. Графиком является прямая, проходящая через точку (0; 5) и параллельная оси х.
4. Решим уравнение:
х = 1, значит, абсцисса точки пересечения графиков равна 1. Найдем соответствующее значение ординаты:
если х = 1, то у = –14 · 1 + 32 = 18.
Точка пересечения имеет координаты (1; 18).
5. График параллелен прямой у = 2х + 9, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 2х.
а) Если х = –3,5, то у = 2 · (–3,5) – 15 = –7 – 15 = –22;
б) если у = –5, то 2х – 15 = –5;
–5 = 5 – неверно, значит, график функции не проходит через точку
K (10; –5).
Ответ: а) –22; б) 5; в) не проходит.
Построим две точки, принадлежащие графику:
если х = 0, то у = –3 · 0 – 3 = –3;
если х = –2, то у = (–3) · (–2) – 3 = 3.
б) Если у = –6, то х = 1.
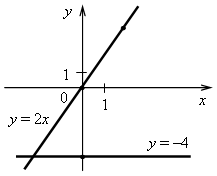
3. а) у = 2х. Графиком является прямая, проходящая через начало координат и точку (2; 4).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.
4. Решим уравнение:
х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты:
если х = 2, то у = –10 · 2 – 9 = –29.
Точка пересечения имеет координаты (2; –29).
5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х.
III. Итоги урока.
IV. Домашнее задание: повторить п. 8–10 и подготовиться к устному опросу.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Подготовка к контрольной работе по теме «Линейные уравнения, функция, неравенства»
Подготовка к контрольной работе
Линейные уравнения. Линейные неравенства. Линейная функция
1. Выберите точку, принадлежащую графику функции 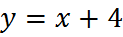
2. Найдите значение функции 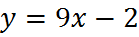
3. Решите неравенства:
а) 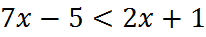
б) 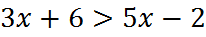
4. Постройте график функции 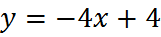
5. Катер за 4 часа проходит против течения реки такое же расстояние, какое проходит за 2 часа по течению. Найдите собственную скорость катера, если скорость течения реки 4 км/ч.
6. Решите неравенства:
а) 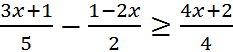
б) 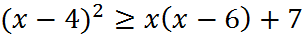
7. Докажите, что уравнение не имеет корней:
🔥 Видео
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Линейная функция и ее график. 7 класс.Скачать

ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

Контрольная работа 3. Линейные уравнения, Линейная функция. Вариант 2. Алгебра 7 классСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Алгебра 7 класс. Контрольная работа №3. Линейная функцияСкачать

Линейная функция и её график. Алгебра, 7 классСкачать

Линейная функция. Нахождение формулы линейной функцииСкачать

Контрольная работа по теме "Линейная функция и ее график", 7 класс.Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Математика это не ИсламСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать