учебно-методический материал по геометрии (10 класс) по теме
Контрольные работы по геометрии для 10 и 11 класса к УМК Л. С. Атанасяна и др.
Видео:Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Контрольные работы по геометрии для 10 класса | 23.46 КБ |
| контрольные работы по геометрии для 11 класса | 52.32 КБ |
Видео:Уравнение плоскости. 11 класс.Скачать

Предварительный просмотр:
КОНТРОЛЬНАЯ РАБОТА № 1
ТЕМА: ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ ?
б) Чему равен угол между прямыми ЕF и АВ , если АВС = 150°? Поясните.
2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС . Точка Р – середина стороны AD , а K – середина стороны DC .
а) Каково взаимное положение прямых РK и АВ ?
б) Чему равен угол между прямыми РK и АВ , если АВС = 40° и ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD , М и N – середины сторон АВ и ВС соответственно; Е CD , K DA , DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
КОНТРОЛЬНАЯ РАБОТА № 2
ТЕМА: ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ. ТЕТРАЭДР И ПАРАЛЛЕЛЕПИПЕД.
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
Сделайте рисунок для каждого возможного случая.
2. Через точку О , лежащую между параллельными плоскостями α и β, проведены прямые l и m . Прямая l пересекает плоскости α и β в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 2 В 2 , если А 1 В 1 = 12 см, В 1 О : ОВ 2 = 3 : 4.
3. Изобразите параллелепипед ABCDA 1 B 1 C 1 D 1 и постройте его сечение плоскостью, проходящей через точки M , N и K , являющиеся серединами ребер АВ , ВС и DD 1 .
1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А 1 и А 2 соответственно, прямая m – в точках В 1 и В 2 . Найдите длину отрезка А 1 В 1 , если А 2 В 2 = 15 см, ОВ 1 : ОВ 2 = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
КОНТРОЛЬНАЯ РАБОТА № 3
ТЕМА: ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
1. Диагональ куба равна 6 см. Найдите:
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a , один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D .
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM ,
М α.
в) найдите синус угла между плоскостью ромба и плоскостью α
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения
относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а . Через сторону AD проведена плоскость α на расстоянии от точки В .
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM ,
М α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
КОНТРОЛЬНАЯ РАБОТА № 4
1. Основанием пирамиды DABC является правильный треугольник АВС , сторона которого равна а . Ребро DA перпендикулярно к плоскости АВС , а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA 1 B 1 C 1 D 1 является ромб ABCD , сторона которого равна а и угол равен 60°. Плоскость AD 1 C 1 составляет с плоскостью основания угол в 60°. Найдите:
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA 1 B 1 C 1 D 1 является параллелограмм ABCD, стороны которого равны a
и 2 a , острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС 1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Предварительный просмотр:
Контрольная работа № 1. Векторы в пространстве
- Найдите координаты вектора , если А(5; -1; 3), В(2; -2; 4).
- Даны векторы и . Найдите .
- Изобразите систему координат Охуz и постройте точку А( 1; -2; -4) . Найдите расстояние от этой точки до координатных плоскостей.
- Вершины Δ АВС имеют координаты:
А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ) .
Найдите координаты вектора , если ВМ – медиана ∆ АВС .
- Найдите координаты вектора , если
- Даны векторы и . Найдите .
- Изобразите систему координат Охуz и постройте точку В( -2; -3; 4) . Найдите расстояние от этой точки до координатных плоскостей.
- Вершины ∆ АВС имеют координаты:
А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ) .
Найдите координаты вектора , если АМ – медиана ∆ АВС.
Контрольная работа № 2 . Метод координат в пространстве
- Даны векторы , и , причем:
а) ; б) значение т , при котором .
- Найдите угол между прямыми АВ и СD ,
если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3) и D(1; 2; 2).
- Дан правильный тетраэдр DАВС с ребром а . При симметрии относительно плоскости АВС точка D перешла в точку D 1 . Найдите DD 1 .
1. Даны векторы , и , причем: Найти:
а) ; б) значение т , при котором .
- Найдите угол между прямыми АВ и СD ,
если А(1; 1; 2), В(0; 1; 1), С(2; -2; 2) и D(2; -3; 1).
- Дан правильный тетраэдр DАВС с ребром а . При симметрии относительно точки D плоскость АВС перешла в плоскость А 1 В 1 С 1 . Найдите расстояние между этими плоскостями.
Контрольная работа № 3. Цилиндр. Конус и шар
1. Радиус основания цилиндра равен 5 см , а высота цилиндра равна 6 см . Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
2. Радиус шара равен 17 см . Найдите площадь сечения шара, удаленного от его центра на 15 см .
3. Радиус основания конуса равен 3 м , а высота 4 м . Найдите образующую и площадь осевого сечения.
1. Высота цилиндра 8 дм , радиус основания 5 дм . Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.
2. Радиус сферы равен 15 см . Найдите длину окружности сечения, удаленного от центра сферы на 12 см .
3. Образующая конуса l наклонена к плоскости основания под углом в 30 0 . Найдите высоту конуса и площадь осевого сечения.
Контрольная работа № 4
Объемы тел. Объем призмы, цилиндра, конуса
1. Образующая конуса равна 60 см , высота 30 см . Найдите объём конуса.
2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 45 0 . Объем призмы равен 108 см 3 . Найдите площадь полной поверхности призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна см . Найдите объем цилиндра.
1. Образующая конуса, равная 12 см , наклонена к плоскости основания под углом 30 0 . Найдите объём конуса.
2. Основанием прямой призмы является ромб со стороной 12 см и углом 60 0 . Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна см . Найдите объем цилиндра.
Контрольная работа № 5. Объем шара и площадь сферы
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 60 0 . Найдите отношение объёмов конуса и шара.
2. Объём цилиндра равен 96π см 3 , площадь его осевого сечения 48см 2 . Найдите площадь сферы, описанной около цилиндра.
3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р , а прилежащий угол равен . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол . Найдите объём конуса.
1. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.
2. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р , а прилежащий угол равен . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол . Найдите объём цилиндра.
Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Контрольные работы по геометрии 11 класс Атанасян Л.С.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Контрольная работа №1 по теме: «Векторы. Метод координат в пространстве»



1. 




2. 



3. Вершины ∆ АВС имеют координаты А(2; 1; -8); В( 1; -5; 0);
С(8; 1;-4). Докажите, что треугольник равнобедренный.
4. 



1. 







2. 



3. Вершины ∆ АВС имеют координаты А(-1; 5; 3); В( -3; 7; 5);
С(3; 1;-5). Докажите, что треугольник равнобедренный.
4. 



Контрольная работа №2 по теме « Цилиндр. Конус. Шар»
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120 
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30 
б ) площадь боковой поверхности конуса.
3. Диаметр шара равен 20см. Через конец диаметра проведена плоскость под углом 45 
1. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найти площадь полной поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30 
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60 
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 16 см. Через конец диаметра проведена плоскость под углом 30 
Контрольная работа №3 по теме « Объёмы тел»
1. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые. Размеры на рис. даны в см.
2. Найдите высоту конуса, если его объем 48 π см 3 , а радиус основания 4 см.
3. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
4. В цилиндр вписана призма с боковым ребром 
5. Объем шара равен 500 π см 3 . На радиусе как на диаметре построен другой шар. Найдите объем малого шара.
Контрольная работа №3 по теме « Объёмы тел»
1. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые. Размеры на рис. даны в см.
2. Найдите радиус основания конуса, если его высота 3 см, а объем 75 π см 3 .
3. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45 
4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 
5. Объем шара равен 24 π см 3 . На диаметре как на радиусе построен другой шар. Найдите объем большего шара.
Итоговая контрольная работа
1. Даны точки А (1;3;2), В (0;2;4), С (1;1;4), Д (2;2;2).
а) Определите вид четырехугольника АВСД.
б) Найдите координаты точки пересечения диагоналей четырехугольника АВСД.
2. Высота правильной треугольной призмы 12 см, а высота основания 5 см. Найдите:
а) площадь полной поверхности призмы, б) объем призмы
3. В правильной четырехугольной пирамиде SA В CD сторона основания равна 4 см, боковое ребро 5 см. Найдите:
а) площадь боковой поверхности пирамиды,
б) объем пирамиды
в) угол между боковой гранью и плоскостью основания.
1. Даны точки: А(0;1 ;-1), В(1;-1; 2), С(3;1;0). Найдите угол между векторами АВ и АС
2. Высота правильной четырехугольной призмы равна 12 см, а диагональ основания 10 см. Найдите:
а) площадь полной поверхности призмы,
б) объем призмы
3. В правильной треугольной пирамиде SABCD сторона основания равна 4 см, а боковое ребро равно 5 см.
Найдите
а) площадь боковой поверхности пирамиды,
б) объем пирамиды.
Видео:11 класс, 8 урок, Уравнение плоскостиСкачать

Контрольные работы по геометрии 11 класс Атанасян
Геометрия 11 Контрольная работа № 1 Л. С. Атанасян, В. Ф Бутузов, С. Б. Кадомцев
«Координаты точки. Координаты вектора» Л. С Киселёв, Э. Г. Позняк
Просмотр содержимого документа
«Контрольные работы по геометрии 11 класс Атанасян»
Геометрия 11 Контрольная работа № 1 Л. С. Атанасян, В. Ф Бутузов, С. Б. Кадомцев
«Координаты точки. Координаты вектора» Л. С Киселёв, Э. Г. Позняк
(на 20 мин)
1. Найдите координаты вектора 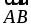
2. Даны векторы 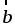
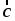
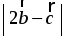
3. Изобразите систему координат Oxyz и постройте точку А (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей.
Геометрия 11 Контрольная работа № 1 Л. С. Атанасян, В. Ф Бутузов, С. Б. Кадомцев
«Координаты точки. Координаты вектора» Л. С Киселёв, Э. Г. Позняк
(на 20 мин)
1. Найдите координаты вектора 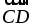
2. Даны вектора 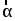
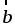
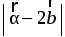
3. Изобразите систему координат Oxyz и постройте точку В (– 2; – 3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Геометрия 11 Контрольная работа № 2 Л. С. Атанасян, В. Ф Бутузов, С. Б. Кадомцев
«Скалярное произведение векторов. Движения» Л. С Киселёв, Э. Г. Позняк
1. Вычислите скалярное произведение векторов 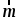
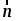
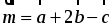
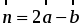
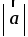
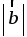
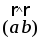
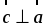
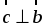
3. При движении прямая отображается на прямую b1, а плоскость β – на плоскость β1 и b || β1.
📸 Видео
Уравнение прямой в пространстве. 11 класс.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости. Практическая часть. 11 класс.Скачать

Видеоурок "Уравнение плоскости в отрезках"Скачать

Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

11. Прямая в пространстве и ее уравненияСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Геометрия 11 класс (Урок№1 - Координаты в пространстве. Система координат.)Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Математика это не ИсламСкачать

5. Нормальное уравнение плоскости выводСкачать



