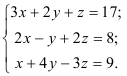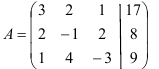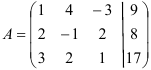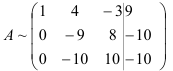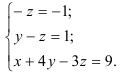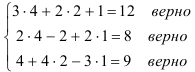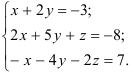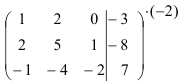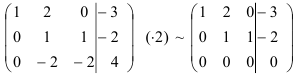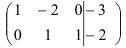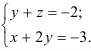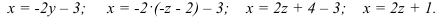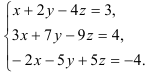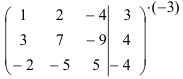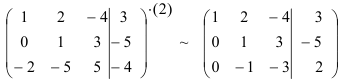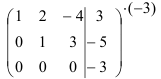Системы линейных уравнений
Задание: Решение систем линейных уравнений по правилу Крамера и методом Гаусса.
Цель: формирование умения решать системы линейных уравнений по правилу Крамера и методом Гаусса.
Задание для самостоятельной внеаудиторной работы:
5.1. Изучите теоретические основы решения системы линейных уравнений по правилу Крамера и методом Гаусса.
5.2. Решите систему уравнений, используя правило Крамера:
5.3. Решите систему линейных уравнений по методу Гаусса:
5.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?
Методические указания по выполнению работы:
Для решения систем линейных уравнений применяют правило Крамера и метод Гаусса.
1. Правило Крамера решения системы 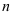
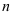
Система 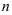
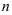

где 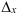

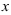
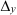

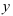
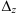

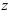
- Пример 1.
- Пример 2.
- Пример 3.
- Пример 4.
- Контрольная работа по алгебре на тему «Системы линейных уравнений с двумя неизвестными» (7 класс)
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Вариант 10 Решить методом Жордана–Гаусса систему линейных уравнений
- 🔥 Видео
Пример 1.
Решите систему уравнений по правилу Крамера:
Решение:
Составим определитель 
Определитель 
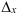
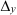
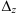
По правилу Крамера найдем неизвестные:
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
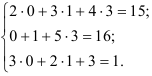
Итак, решение системы найдено правильно.
Ответ:
2. Метод Гаусса решения систем линейных уравнений
- Составьте расширенную матрицу системы — матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов.
- С помощью элементарных преобразований приведите полученную матрицу к ступенчатому виду.
- Восстановите систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и найдите значения неизвестных.
Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:
- число уравнений не равно числу неизвестных.
- если в правиле Крамера
.
Ответ на вопрос о существовании и количестве решений системы линейных уравнений дает теорема Кронекера-Капелли (критерий совместности системы линейных уравнений): система линейных уравнений с 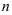
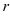
- если
(ранг матрицы равен числу неизвестных), то система имеет единственное решение;
- если
(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
Все возможные случаи решения системы линейных уравнений (одно решение, нет решений, множество решений) разобраны в примерах 2-4.
Пример 2.
Решите систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу системы и приведем её к ступенчатому виду:
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов
при последующих вычислениях.
Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом 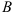
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:
Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:
Восстановим из полученной матрицы 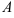
Из последнего уравнения находим: 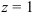
Подставим 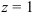
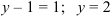
После подстановки 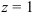
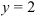
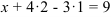
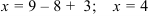
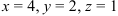
Следовательно, решение системы найдено верно.
Ответ: 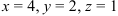
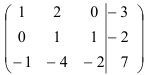
Пример 3.
Найдите все решения системы линейных уравнений:
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-2) и сложим ее со второй строкой:
Сложим первую и третью строки:
Домножим вторую строку на 2 и сложим ее с третьей строкой:
Вычеркнем нулевую строку:
Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум. Следовательно, в силу критерия Кронеккера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (три), то система имеет бесчисленное множество решений. Найдем эти решения.
Восстановим систему уравнений, равносильную исходной:
Пусть 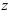
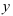
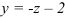
Подставим данное выражение 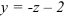
Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: 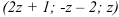
Ответ: 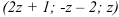
Пример 4.
Докажите, что система линейных уравнений не имеет решений:
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-3) и сложим ее со второй строкой:
Домножим первую строку на 2 и сложим ее с третьей строкой:
Сложим вторую и третью строки:
Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронеккера-Капелли, система не имеет решений.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. Контрольная №7. 7 классСкачать

Контрольная работа по алгебре на тему «Системы линейных уравнений с двумя неизвестными» (7 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений

Контрольная работа №7
Системы линейных уравнений с двумя неизвестными.
1. Решите методом подстановки систему уравнений
2. Решите методом сложения систему уравнений
3. Решите систему уравнений любым из известных вам методов
4. Решите систему уравнений любым из известных вам методов
5. Решите графически систему уравнений
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:7 класс. Контрольная №9 (из 10). Тема: Системы линейных уравнений. Разбираемся в методах! :)Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 589 808 материалов в базе
Материал подходит для УМК
«Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
Глава 7. Системы двух уравнений с двумя неизвестными
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 21.05.2021
- 171
- 7
- 20.05.2021
- 109
- 1
- 20.05.2021
- 107
- 0
- 20.05.2021
- 104
- 2
- 20.05.2021
- 127
- 0
- 20.05.2021
- 103
- 4
- 20.05.2021
- 52
- 1
- 20.05.2021
- 74
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 21.05.2021 557
- DOCX 17.5 кбайт
- 8 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Некрасова Алина Олеговна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 954
- Всего материалов: 2
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
РДШ организовало сбор гуманитарной помощи для детей из ДНР
Время чтения: 1 минута
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Университет им. Герцена и РАО создадут портрет современного школьника
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Только 23 февраля!
Получите новую
специальность
по низкой цене
Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Вариант 10 Решить методом Жордана–Гаусса систему линейных уравнений
Информация о работе
- Тема: Вариант 10 Решить методом Жордана–Гаусса систему линейных уравнений
- Количество скачиваний: 10
- Тип: Контрольная работа
- Предмет: Математика
- Количество страниц: 9
- Язык работы: Русский язык
- Дата загрузки: 2014-11-03 20:46:41
- Размер файла: 60.98 кб
Помогла работа? Поделись ссылкой
- Вариант 10 Решить методом Жордана–Гаусса систему линейных уравнений [Электронный ресурс]. – URL: https://www.sesiya.ru/kontrolnaya-rabota/matematika/variant-10-reshit-metodom-jordana%E2%80%93gaussa-sistemu-lineynyh-uravneniy/ (дата обращения: 23.02.2022).
- Вариант 10 Решить методом Жордана–Гаусса систему линейных уравнений // https://www.sesiya.ru/kontrolnaya-rabota/matematika/variant-10-reshit-metodom-jordana%E2%80%93gaussa-sistemu-lineynyh-uravneniy/.
Есть ненужная работа?
Добавь её на сайт, помоги студентам и школьникам выполнять работы самостоятельно
- О документе
- Скачать документ
Информация о документе
Документ предоставляется как есть, мы не несем ответственности, за правильность представленной в нём информации. Используя информацию для подготовки своей работы необходимо помнить, что текст работы может быть устаревшим, работа может не пройти проверку на заимствования.
Если Вы являетесь автором текста представленного на данной странице и не хотите чтобы он был размешён на нашем сайте напишите об этом перейдя по ссылке: «Правообладателям»
Можно ли скачать документ с работой
Да, скачать документ можно бесплатно, без регистрации перейдя по ссылке:
Задание 4
Решить методом Жордана–Гаусса систему линейных уравнений:
Запишем систему в виде:
-2 3 -1 0
4 -2 5 1
3 -4 0 10
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (-2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (-2), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 -1.5 0.5 0
0 4 3 1
0 0.5 -1.5 10
Разрешающий элемент равен (4). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 0 1.63 0.38
0 1 0.75 0.25
0 0 -1.88 9.88
Разрешающий элемент равен (-1.88). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 0 0 8.93
0 1 0 4.2
0 0 1 -5.27
x1 = 8.93
x2 = 4.2
x3 = -5.27
Задание 5
Решить графически задачу линейного программирования:
Необходимо найти минимальное значение целевой функции F = 3×1-2×2 → min, при системе ограничений:
-x1+x2≤4 (1)
-3×1+x2≥-6 (2)
x1+x2≥6 (3)
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Границы области допустимых решений
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
Рассмотрим целевую функцию задачи F = 3×1-2×2 → min.
Построим прямую, отвечающую значению функции F = 0: F = 3×1-2×2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (3; -2). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
Область допустимых решений представляет собой линию.
Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
-x1+x2=4
x1+x2=6
Решив систему уравнений, получим: x1 = 1, x2 = 5
Откуда найдем минимальное значение целевой функции:
F(X) = 3*1 — 2*5 = -7
Задание 6
Решить симплексным методом следующие задачи линейного программирования:
Определим минимальное значение целевой функции F(X) = 2×1 + 3×2 — 3×3 при следующих условиях-ограничений.
2×1 — 3×2 + x3≤8
x1 + 2×2 + 2×3≤4
3×1 — 2×2 + x3≤12
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6.
2×1-3×2 + 1×3 + 1×4 + 0x5 + 0x6 = 8
1×1 + 2×2 + 2×3 + 0x4 + 1×5 + 0x6 = 4
3×1-2×2 + 1×3 + 0x4 + 0x5 + 1×6 = 12
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
A = 2 -3 1 1 0 0
1 2 2 0 1 0
3 -2 1 0 0 1
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x4, x5, x6
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,8,4,12)
Базисное решение называется допустимым, если оно неотрицательно.
Базис B x1 x2 x3 x4 x5 x6
x4 8 2 -3 1 1 0 0
x5 4 1 2 2 0 1 0
x6 12 3 -2 1 0 0 1
F(X0) 0 -2 -3 3 0 0 0
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент .
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (8 : 1 , 4 : 2 , 12 : 1 ) = 2
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
Базис B x1 x2 x3 x4 x5 x6 min
x4 8 2 -3 1 1 0 0 8
x5 4 1 2 2 0 1 0 2
x6 12 3 -2 1 0 0 1 12
F(X1) 0 -2 -3 3 0 0 0 0
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x5 в план 1 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=2
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x3 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x3 и столбец x3.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент (2), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
B x 1 x 2 x 3 x 4 x 5 x 6
8-(4 • 1):2 2-(1 • 1):2 -3-(2 • 1):2 1-(2 • 1):2 1-(0 • 1):2 0-(1 • 1):2 0-(0 • 1):2
4 : 2 1 : 2 2 : 2 2 : 2 0 : 2 1 : 2 0 : 2
12-(4 • 1):2 3-(1 • 1):2 -2-(2 • 1):2 1-(2 • 1):2 0-(0 • 1):2 0-(1 • 1):2 1-(0 • 1):2
0-(4 • 3):2 -2-(1 • 3):2 -3-(2 • 3):2 3-(2 • 3):2 0-(0 • 3):2 0-(1 • 3):2 0-(0 • 3):2
Получаем новую симплекс-таблицу:
Базис B x1 x2 x3 x4 x5 x6
x4 6 3/2 -4 0 1 -1/2 0
x3 2 1/2 1 1 0 1/2 0
x6 10 5/2 -3 0 0 -1/2 1
F(X1) -6 -7/2 -6 0 0 -3/2 0
1. Проверка критерия оптимальности.
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
Базис B x1 x2 x3 x4 x5 x6
x4 6 3/2 -4 0 1 -1/2 0
x3 2 1/2 1 1 0 1/2 0
x6 10 5/2 -3 0 0 -1/2 1
F(X2) -6 -7/2 -6 0 0 -3/2 0
Оптимальный план можно записать так:
x3 = 2
F(X) = -3•2 = -6
Задание 7
Решить транспортную задачу. Имеются четыре пункта поставки однородного груза , , , , в каждом из которых находится груз соответственно в количестве , , , тонн и пять пунктов потребления этого груза , , , , . В пункты , , , , требуется доставить соответственно , , , , тонн груза. Транспортные расходы при перевозке единицы груза из пункта в пункт равны , где i=1, 2, 3, 4, j=1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, учитывая: ,
,
.
🔥 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение систем уравнений методом подстановкиСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение системы неравенствСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Контрольная работа №7 по алгебре, 7 класс. Система линейных уравненийСкачать

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по алгебре 7 классСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

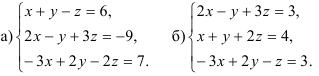
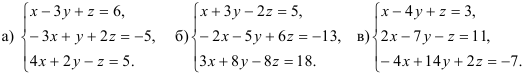
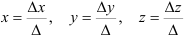

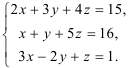
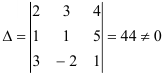
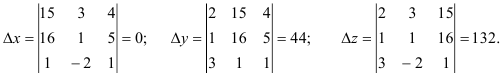
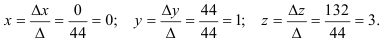
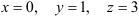
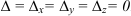 .
.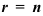 (ранг матрицы равен числу неизвестных), то система имеет единственное решение;
(ранг матрицы равен числу неизвестных), то система имеет единственное решение;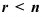 (ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.