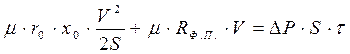Константы в уравнении фильтрования отношение объема осадка к объему фильтрата (4 видео)

Лабораторная работа №6.Определение констант процесса фильтрования

Цель работы: изучить процесс фильтрования, освоить методику определения постоянных в уравнении фильтрования и производительности фильтра.

Теоретические сведения

Разделение гомогенных и гетерогенных систем методом фильтрации различают по способам осуществления этого процесса и применяемым для этого в промышленности аппаратам.

Гомогенные системы состоят из одной фазы, внутри которой нет поверхности раздела соприкосновения частей смеси, отличающихся друг от друга по составу и свойствам.

Перегонка и ректификация — частичное или полное разделение гомогенных жидких смесей на компоненты в результате различия их летучести и противоточного взаимодействия жидкости и пара.

Разделение веществ с помощью электрофореза или седиментации основано на различии в скоростях направленного перемещения частиц растворенных веществ относительно неподвижного растворителя под действием соответственно электростатического и центробежного полей. В обоих случаях разделение происходит в пределах одной фазы, т. е. в гомогенной системе.

Экстракция есть процесс разделения гомогенной смеси двух или более веществ на ее компоненты или группы компонентов путем образования системы из двух жидких фаз при помощи вспомогательной жидкости.

Мембранные технологии — технологии, относящиеся к процессу разделения жидких смесей на полупроницаемых перегородках (их называют баромембранными технологиями). Внешне они похожи на обычную фильтрацию, так как движущей силой процесса является разность давлений. В действительности с помощью полунепроницаемых мембран разделяются истинные растворы (гомогенные системы), в то время как фильтрованием можно лишь разделить суспензию, т.е. отделить твердую фазу от жидкой.

Считая мембранные методы фильтрованием на молекулярном уровне, можно условно разместить мембранные методы следующим образом: обратный осмос, нанофильтрация, ультрафильтрация и микрофильтрация по порядку увеличения размера и молекулярной массы задерживаемых частиц.

Гетерогенные системы состоят из внешней (сплошной) фазы и внутренней (дисперсной) фазы. Разделение гетерогенных систем осуществляется на основе различных принципов, использующих, например, разность плотностей разных фаз, или задержании одной из фаз на проницаемой перегородке, пропускающей сплошную фазу (жидкость или газ), называемым фильтрованием и другие.

Гравитационное осаждение суспензий и газовзвесей, в которых дисперсная фаза имеет большую плотность, чем сплошная среда осуществляется в аппаратах, называемых отстойниками. Загружаемая в ёмкость суспензия в продолжении цикла осаждения разделяется на осветлённую жидкость (верхний слой) и уплотнённый слой осадка (нижний слой), которые затем раздельно удаляются.

Разделение газовзвесей осуществляют в электростатическом поле промышленных электрофильтров, где используется взаимодействие капель или твёрдых частиц с электродом.

Фильтрование является одним из наиболее широко применяемых в промышленности методов разделения неоднородных систем. Как способ разделения гетерогенных систем фильтрование обеспечивает более полную очистку газовзвесей и суспензий от твёрдых частиц, по сравнению с методом осаждения.

По степени фильтрации различают:

— фильтрование с образованием осадка на фильтровальной перегородке с содержанием в фильтруемой суспензии более 1 % объёмной твёрдой фазы;

сгущение с отделением твёрдой фазы от жидкой в виде высококонцентрированной (сгущённой) суспензии;

осветление — фильтрование жидкостей с незначительным содержанием твёрдой фазы (около 0,1-1 %).

По принципу устройства простейший аппарат для фильтрования, так называемый нутч-фильтр, представляет собой цилиндрический сосуд, разделённый проницаемой перегородкой на две части. В его верхнюю часть подаётся суспензия, которая давит на перегородку, в нижней части скапливается фильтрат.

Классифицируются аппараты фильтрации по режиму работы на фильтры непрерывного и периодического действия, а также по величине рабочего давления фильтрования на фильтры, работающие под давлением и вакуум-фильтры.

Фильтры, работающие под давлением, различаются на:

1) фильтры периодического действия:

фильтрпрессы; нутч-фильтры закрытые; мешочные фильтры; патронные фильтры;

2) фильтры непрерывного действия:

барабанные фильтры; дисковые фильтры.

Вакуум-фильтры различаются на:

1) фильтры периодического действия:

нутч-фильтры закрытые; мешочные фильтры;

2) фильтры непрерывного действия:

барабанные фильтры; дисковые фильтры; карусельные фильтры; ленточные фильтры.

Движущей силой фильтрования является разность давлений по обе стороны фильтровальной перегородки. Она может быть создана различными способами:

1) гидростатическим давлением столба суспензии, подаваемой на фильтр (ДР-> 0,5 МПа);
2) подачей суспензии на фильтр под давлением (ДР—> 0,05 -0,3 МПа);
3) создание вакуума под фильтровальной перегородкой (ДР—> 0,05 — 0,09 МПа);
4) при помощи центробежной силы.

Производительностью аппарата для фильтрования называю скорость фильтрования, которая прямо пропорциональна суммарному сопротивлению, оказываемому фильтрованию перегородкой и слоем осадка/і.

В промышленности применяются три режима фильтрования, характеризуемые интенсивностью прохождения потока фильтрата через перегородку во времени:

1. Фильтрация при постоянном потоке фильтрата во времени, которая может обеспечиваться нагнетанием суспензии поршневым насосом. При этом увеличение слоя осадка h на перегородке, сопровождаемое ростом сопротивления потоку фильтрата, происходит при непрерывном увеличении перепада давлений ДР.
2. Фильтрация с использованием подачи сжатого воздуха на суспензию перед перегородкой компрессором, или созданием разрежения после перегородки с помощью вакуум-насоса. При этом перепад давлений ДР остается постоянным по мере увеличения слоя осадка h и, следовательно, поток фильтрата и производительность во времени уменьшаются.
3. Фильтрация при подаче суспензии центробежным насосом. При увеличении во времени слоя осадка //перепад давлений ДР увеличивается в оптимальных пределах рабочей характеристики насоса. Этот процесс сопровождается уменьшением потока фильтрата.

Фильтровальная перегородка, как важнейшая часть аппарата для фильтрования, должна обладать достаточной механической прочностью, низким гидравлическим сопротивлением и химической стойкостью. Выбор типа материала, из которого изготовлена фильтровальная перегородка осуществляется опытным путём, в зависимости от дисперсности частиц осадка, вязкости суспензии и её химической агрессивности. Широко применяются перегородки из различного вида тканей (полимерных, шерстяных, хлопчатобумажных, металлических, стекловолоконных), металлических сеток, нетканых материалов, волокон. Использование пористых керамических и металлокерамических плиток ограничено трудноизвлекаемостью из пор остатков осадка. При этом такие плитки отличаются длительным сроком их эксплуатации. По принципу действия различают фильтровальные перегородки гибкие и негибкие; гибкие бывают металлические и неметаллические, а негибкие — жесткие и нежесткие.

Осадки, получаемые при фильтровании бывают сжимаемые (гидроксиды металлов) и несжимаемые (песок, карбонат кальция и др.), в последнем случае поток жидкости через фильтровальную перегородку ламинарен и скорость фильтрования пропорциональна перепаду давлений АР и высоте слоя осадка h. Скорость процесса в этом случае описывается уравнением Дарси:

где dV/S-dx — скорость процесса фильтрования, м 3 /(м 2 -с); х -продолжительность фильтрования (с); АР — разность давлений (Па); ц -вязкость фильтра (Па с); го- удельное объёмное сопротивление осадка (т.е. сопротивление, оказываемое потоку фильтрата слоем осадка толщиной 1м) (м’ 2 ); хо- отношение объёма осадка к объёму фильтра; Кфп- сопротивление фильтрованной перегородки, (м’ 1 ).

В случае сжимаемых осадков эта зависимость более сложна и индивидуальна для каждой суспензии.

Для предотвращения закупорки пор применяют вспомогательные вещества (диатомит, перлит, асбест и др.), которые образуют защитные сводики над порами. Для предотвращения сжатия осадков и уменьшения ИХ сопротивления (7?ос = ro’Xo’h) к суспензиям добавляют коагулянты и флокулянты, способствующие агрегированию мелких частиц.

Методика расчета процесса фильтрования сводится к определению констант процесса. Путем интегрирования (6.1) принимает вид

— = МV + N ,(6.2)где _{м =} ‘ г о ‘ х о , дг = .

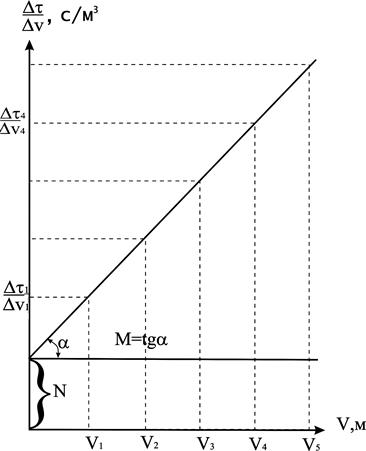
При постоянной температуре и перепаде давлений величины М и N являются тоже постоянными. В координатах V, г/У (6.2) интегральное уравнение фильтрования изображается прямой линий, тангенс угла наклона которой к оси абсцисс равен М, а отрезок, отсекаемый прямой линией на оси ординат, равен N (рис. 6.1).

Рис. 6.1. К определению постоянных процесса фильтрования

Константы процесса определяются по следующим зависимостям:

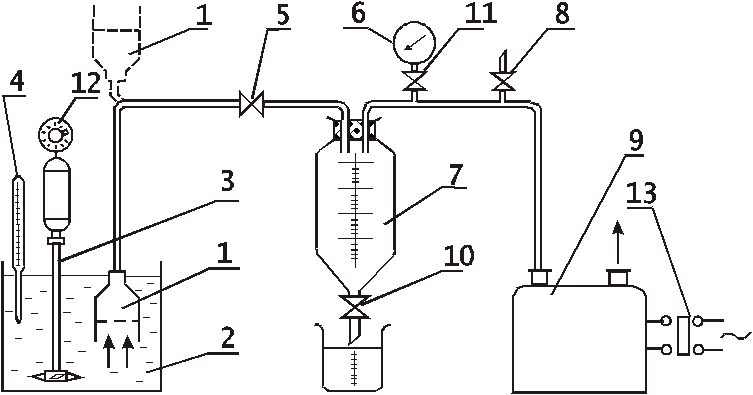
Установка, изображенная на рис. 6.2, состоит из вакуум-фильтра с мешалкой 2, (воронка 1, на дно которой помещается фильтровальная перегородка и сборник фильтрата), влагоотделителя 9, вакуум-насоса 10. Температура суспензии измеряется термометром 3, создаваемое разряжение — вакуумметром 7.

Порядок выполнения работы

1. Приготовить суспензию мел — вода в соотношении 1:3 (по объему).
2. Включить вакуум насос 10, установить с помощью краника 8 заданное разряжение, кран 6 закрыт.
3. Включаем мешалку 2, заливаем суспензию в воронку 1.
4. Открываем кран 6, отмечаем время наполнения сборника 4 через каждые 20 мл.
5. Выключить установку. Замерить толщину слоя осадка h.
6. Результаты замеров занести в таблицы.

Обработка результатов измерений

Результаты замеров заносят в следующие таблицы и проводят обработку полученных данных:

Время замера т,с

Отношение времени фильтрования к объему фильтрата т IV

Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

ОПРЕДЕЛЕНИЕ КОНСТАНТ ПРОЦЕССА ФИЛЬТРАЦИИ

Объем фильтрата V, полученный за промежуток времени с единицы поверхности фильтра, пропорционален разности давлений DР и обратно пропорционален вязкости фильтрата и общему сопротивлению осадка R_ОС и фильтровальной перегородки R_Ф.П_.. В дифференциальной форме это можно написать так:

, (5.1)

где t – продолжительность фильтрования, с; S – поверхность фильтрования, м 2 .

Величина – называется скоростью фильтрования (5.2).

Движущей силой процесса фильтрования служит разность давлений по обе стороны фильтрующей перегородки. Эта разность может быть создана:

а) слоем самой суспензии, налитой на фильтр;

б) подачей суспензии на фильтр под давлением (например, в фильтрпрессах давление достигает 12 атм);

в) создание вакуума под фильтрующей перегородкой (в промышленных вакуум-фильтрах вакуум составляет 600–660 мм.рт.ст.). Величину R_ФП в процессе фильтрования в первом приближении можно принимать постоянной, пренебрегая некоторым его увеличением вследствие, проникания в поры перегородки новых твердых частиц. R_ОС с увеличением количества осадка изменяется от нуля до максимального значения в конце процесса.

Учитывая пропорциональность объемов осадка и фильтрата, обозначим отношение объема осадка к объему фильтрата x₀. Тогда объем осадка будет равен х₀ ×V. Вместе с тем объем осадка равен h_ОС× S, где h_ОС – высота слоя осадка. Следовательно,

(5.3)

Сопротивление слоя осадка можно выразить равенством:

(5.4)

где r₀ – удельное объемное сопротивление слоя осадка – характеризует сопротивление потоку жидкой фазы равномерным слоем осадка толщиной 1 м.

Подставив значение R_ОС в уравнение (5.1), получим:

(5.5)

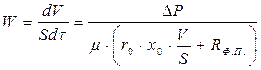
Уравнение (5.5) называется основным дифференциальным уравнением фильтрования. При интегрировании этого уравнения необходимо принимать во внимание условия процесса фильтрования, который может протекать:

а) при постоянной разности давлений;

б) с постоянной скоростью фильтрования;

в) при постоянных Р и W, при переменных Р и W.

При применении вакуум–насосов и компрессоров фильтр присоединяют к вакуум–ресиверу сжатого воздуха и проводят фильтрование при постоянной DP. Для вакуум–насосов в производственных условиях DР находится в пределах 5–9 Н/см 2 . Скорость фильтрования непрерывно уменьшается вследствие возрастания толщины осадка и увеличения его сопротивления.

Если при фильтровании применяют поршневой насос, процесс протекает с постоянной скоростью (определяемой производительностью насоса), при возрастающей разности давлений DР, увеличивающейся с увеличением толщины осадка. В случае использования центробежного насоса DР и W изменяется непрерывно.

Фильтрование под действием гидростатического давления суспензии в производственных условиях применяется сравнительно редко.

Уравнение (5.5) берется в основу технологического расчета промышленного фильтра любой конструкции. Целью этого расчета является определение необходимой поверхности фильтрования S при заданной производительности фильтра или определение действительной производительности фильтра, имеющего известную поверхность S. Для этого должны быть известны величины х₀, r₀, R_Ф.П., которые называются постоянными в уравнении фильтрования или константами фильтрования. Существуют различные способы определения х₀, r₀, R_Ф.П.

Для осадков, встречающихся в химических производствах и состоящих, как правило, из частиц размером не менее 100 мк, эти величины находят экспериментально.

В данной работе рассматривается один из способов опытного определения констант фильтрования для фильтрования при постоянной разности давлений. Этот способ отличается большой точностью получаемых результатов.

При DP=const и неизменной температуре для фильтра данной конструкции и выбранной фильтровальной перегородки все входящие в уравнение (5.5) величины, за исключением V и t, постоянны. Проинтегрируем это уравнение в пределах от 0 до V и от 0 до t:

(5.6)

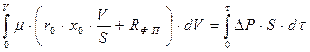
Разделим обе части уравнения на , получим

(5.7)

Преобразуем уравнение (5.7) к виду

, (5.8)

где (5.9)

(5.10)

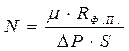
При DP = const и t = const все величины, входящие в правые части равенств (5.9) и (5.10), постоянны. Поэтому значения М и N также постоянны и уравнение (5.8) является уравнением прямой, наклоненной к горизонтальной оси под углом, тангенс которого равен М, и отсекающей на вертикальной оси отрезок N (рис.5.1).

Из уравнения (5.9) и (5.10) следует:

(5.11)

(5.12)

Величину х₀ находят в результате непосредственного измерения объемов осадка и фильтрата.

ЦЕЛЬ РАБОТЫ

1. Ознакомление с методикой экспериментального определения констант фильтрования.

2. Определение производительности фильтра по фильтрату и влажному осадку.

ОПИСАНИЕ ОПЫТНОЙ УСТАНОВКИ

Схема установки представлена на рис. 5.2.

Установка состоит из погружного вакуум–фильтра 1, бачка для суспензии 2 c мешалкой 3, вакуум–насоса 9, приемника для фильтрата 7 и измерительных приборов: термометра 4, вакуумметра 6 и секундомера. Элемент вакуум–фильтра – разборный. Состоит из воронки со съемной решеткой (дырчатый диск) и крышки.

На воронку с решеткой накладывают фильтровальную ткань и прижимают крышкой при помощи четырех болтов.

Отдельные части установки соединены между собой вакуумными резиновыми трубками, как показано на рис. 5.2. На трубках установлен кран 5, которым при работающем вакуум–насосе создают нужный вакуум, и кран 8. Кран 5 открывается после подготовки всей установки к работе на заданном режиме.

Число оборотов мешалки 3 регулируется реостатом 12.

ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ

1. Включают мешалку 3.

2. Собирают вакуум–фильтр I и устанавливают его в баке 2, погружая в суспензию на несколько сантиметров. Закрывают кран 5 и кран 8.

3. Включают вакуум–насос, и открывая кран 8, устанавливают заданный руководителем вакуум по вакуумметру 6.

Рис. 5.2. Схема установки:

1 – вакуум–фильтр, 2 – бачок для суспензии, 3 – мешалка, 4 – термометр, 5 – кран, 10, 11 – краны, 6 – вакуумметр, 7 – приемник фильтрата, 8 – воздушный кран, 9 – вакуум–насос, 12 – реостат, 13 – выключатель.

4. После установки заданного режима открывают кран 5 и одновременно включают секундомер. Первый замер времени делают при появлении первых капель фильтрата в приемнике. Каждый следующий замер времени производят (не выключая секундомера!) через каждые 100 см 3 фильтрата в приемнике. Когда уровень жидкости в приемнике достигнет верхней черты, выключают секундомер, одновременно освобождают фильтр 1, поднимают его вверх на кронштейне так, чтобы резиновая трубка нигде не создавала застоев жидкости. Фильтрующая поверхность фильтра должна быть повернута вверх. При этом сливается в приемник жидкость, находящаяся в фильтре и трубке.

5. Когда поверхность осадка теряет влажный блеск и перестанет изменять свой вид, продувку прекращают, выключая вакуум–насос.

6. Фильтрат из приемника сливается в мерный цилиндр и замеряется общий объем жидкости V_n. Количество фильтрата, добавившееся при продувке, соответствует первому замеру времени (до появления первых капель).

7. Измеряют торцом металлической линейки толщину слоя осадка на фильтре и диаметр всего слоя D.

8. Фильтр 1 разбирают, осадок снимают в специальный бачок, промывают фильтр и ткань, собирают фильтр снова. Результаты замеров заносят в табл. 5.1.

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

, с;

, с; …

,см 3 ;

…

см 3

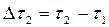
Вычисляют отношение и строят график (рис. 5.3.), откладываюя по оси абцисс V , а по оси ординат величины отношений .

Рис. 5.3. График для определения коэффициентов M и N

Из графика определяются М и N с учетом масштабов графика.

(5.13)

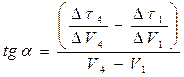
и рассчитывают значения r₀ и R_Ф.П_. по формулам (5.11) и (5.12).

Работу заканчивают определением часовой производительности фильтра по фильтрату и влажному осадку (с 1 м 2 поверхности фильтра).

(5.14)

(5.15)

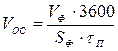
где V_П – общее количество фильтрата, собранное за время опыта, м 3 ; V_ОС – объем осадка, равный , м 2 ; S_Ф – площадь фильтра, м 2 ; t_n – общая продолжительность опыта, сек.

Результаты замеров и расчетов следует свести в таблицу 5.1.

Результаты замеров

№	Время замера t, с	Объем фильтрата V, см 3	Интервалы	, с/м 3	r₀, м -2	R_Ф.П., м -1
времени Dt	Объем фильтрата DV, м 3
1.	t₁	V₁ + 0	DV₁
2.	t₂	V₁ +100	10 -4
3.	t₃	V₁ + 200	10 -4
4.	t₄	V₁ +300	10 -4
5.	t₅	V₁ + 400	10 -4

Отчет по работе включает:

1. Формулировку цели и задачи работы.

2. Схему установки со спецификацией.

3. Сводку расчетных формул.

4. Отчетную таблицу.

5. Примеры расчетов.

6. График, построенный по опытным данным.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Определение гетерогенной системы.

2. Определение суспензии.

3. Определение процесса фильтрации.

4. Цель процесса фильтрации.

5. Движущая сила процесса фильтрации.

6. Способы создания движущей силы фильтрации.

7. Виды фильтрующих перегородок.

8. Чем обусловлен выбор фильтрующей перегородки.

10. Определение несжимаемого осадка.

11. Что понимают под сжимаемым осадком?

12. Понятие об удельном сопротивлении осадка.

13. Может ли удельное сопротивление осадка быть постоянной величиной? Для каких осадков?

14. Классическое уравнение скорости любого физического процесса.

15. Что такое скорость фильтрации?

16. Из каких величин состоит общее сопротивление фильтра?

17. Основное уравнение фильтрации в дифференциальной форме.

18. В каких режимах может протекать процесс фильтрации?

19. Практическая реализация различных режимов фильтрования.

20. Каким образом можно выразить сопротивление осадка?

21. Как выражают объем осадка?

22. Дифференциальное уравнение фильтрования.

23. Цель технологического расчета промышленного фильтра любой конструкции.

24. Что понимают под константами фильтрации?

25. Как определяют константы фильтрации?

26. Основные элементы фильтрпресса.

27. Движение жидкости в фильтрпрессе (схема)

28. Достоинства и недостатки фильтрпресса.

29. Схема нутч–фильтра.

30. Преимущества и недостатки нутч–фильтра.

31. Барабанный вакуум–фильтр (принцип действия).

32. Принципиальная схема ленточного вакуум–фильтра.

34. Порядок проведения работы.

35. Схема лабораторной установки.

36. Как определяют удельное объемное сопротивление осадка?

37. Как определяют сопротивление фильтра?

38. Как определяют производительность по фильтрату?

39. Как определяют производительность фильтра по осадку?

ЛИТЕРАТУРА

1. А.Г.Касаткин Основные процессы и аппараты химической технологии, — М.: Химия, — 1976.

2. А.И.Скобло и др., Процессы и аппараты нефтеперерабатывающей и нефтехимической промышленности, — М., 1982,

3. В.А.Жуков Фильтрование, — М.: Химия, 1972, — 440 с.

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Определение констант процесса фильтрования

Алтайский государственный технический университет

Бийский технологический институт

Методические указания к лабораторной работе по курсу

«Основные процессы и аппараты химической технологии»

для студентов специальностей 251100-ХТОСА,

251200-ХТПК, 070100-БТ, 171200-АПХП

Н, И, Ломоносова констант процесса фильтрования. Методические указания к лабораторной работе по курсу «Основные процессы и аппараты химической технологии» для студентов специальностей 251100-ХТОСА, 251200-ХТПК, 070100-БТ, 170500-АПХП.

Алт. гос. техн. ун-т им. , БТИ, — Бийск

Из-во Алт. гос. техн. ун-та,19с.

В методических указаниях содержится описание правил и порядка проведения лабораторной работы «Определение констант процесса фильтрования», иллюстрирующей устройство и работу вакуум-фильтра и методику определения констант процесса фильтрования.

Рассмотрены и одобрены на заседании кафедры «Процессы аппараты химической технологии»

Протокол № 10 от «03.09.98»

Рецензент: к. т.н., (БТИ Алт. ГТУ им. )

Процессом фильтрования [1] называют процесс разделения неоднородных систем при помощи пористых перегородок, которые задерживают одни фазы этих систем и пропускают другие. К этим процессам относятся разделение суспензий на чистую жидкость и влажный осадок, аэрозолей на чистый газ и сухой осадок или на чистый газ и жидкость. Фильтры разнообразных конструкций широко используются в различных отраслях промышленности для разделения неоднородных систем, для очистки природных и сточных вод. Фильтрование может обеспечить почти полную очистку жидкости или газа от взвешенных частиц и в этом отношении имеет преимущество перед процессами осаждения.

В качестве фильтрующих материалов в промышленных аппаратах используют естественные и искусственные зернистые и пористые тела: песок, гравий, ткани, сетки, пористые керамику и пластические массы.

Значение процессов фильтрования возрастает с увеличением масштабов производства химической и родственных ей отраслей промышленности. Это объясняется тем, что процесс разделения суспензий нередко вызывает затруднения, обусловленные, главным образом, большим сопротивлением осадка и, соответственно, малой скоростью фильтрования. При этом для достижения заданной производительности фильтровальной установки требуется большое число фильтров определенной конструкции. Поэтому возникла тенденция к увеличению размеров фильтровального оборудования и интенсификации процессов фильтрования.

1 КЛАССИФИКАЦИОННЫЕ ПРИЗНАКИ

Разделение суспензий, состоящих из жидкости и взвешенных в ней твердых частиц, производят с помощью фильтра, который в простейшем виде является сосудом, разделенным на две части фильтровальной перегородкой. В разделенных частях сосуда создают разность давлений, под действием которой жидкость проходит через поры фильтровальной перегородки, причем твердые частицы задерживаются на ее поверхности. Таким образом суспензия разделяется на чистый фильтрат и влажный осадок. Разность давлений фильтровальной перегородки создают разными способами, в результате чего осуществляются разные процессы фильтрования.

Фильтрование и фильтры можно классифицировать по нескольким признакам:

1) по движущей силе — фильтрат проходит через фильтрующую перегородку под действием:

а) гидростатического напора (силы тяжести);

б) центробежной силы;

в) создания повышенного давления над перегородкой;

г) создания вакуума под перегородкой;

2) по механизму процесса фильтрования:

а) с образованием осадка на поверхности фильтрующей перегородки;

б) с закупоркой пор фильтрующей перегородки;

3) по целенаправленности процесса — целью процесса фильтрования может быть получение:

а) сухого остатка;

б) чистого фильтрата;

в) сухого остатка и чистого фильтрата одновременно;

4) по принципу действия:

б) периодическое фильтрование;

5) по природе осадка с образованием:

б) несжимаемого осадка;

6) по направлению потока:

Фильтрованием отделяются твердые частицы, средний размер которых одного порядка величины с размерами пор фильтрующей перегородки (1…10 мкм и более).

В промышленных условиях применяют разнообразные, часто довольно сложные по конструкции фильтры, причем фильтровальная перегородка имеет плоскую или цилиндрическую форму.

Фильтры чаще всего подразделяются на фильтры периодически действующие и непрерывно действующие. В первых — фильтровальная перегородка неподвижна, во вторых — она непрерывно перемещается по замкнутому пути. При этом в фильтрах периодического действия на всех элементах перегородки одновременно осуществляются одни и те же процессы, например, поступление суспензии, образование осадка или его удаление. В фильтрах непрерывного действия на различных элементах перегородки происходят разные процессы в зависимости от того, на каком участке замкнутого пути находится в данный момент рассматриваемый элемент перегородки; так, на один участок перегородки поступает суспензия, а на других её участках образуется и удаляется осадок.

2 ОБЩАЯ ТЕОРИЯ ФИЛЬТРОВАНИЯ

Общая теория фильтрования основывается на эмпирическом законе Дарси, установленном в 1856 г., согласно которому скорость фильтрования воды сквозь слой песка пропорциональна гидростатическому давлению и обратно пропорциональна толщине слоя. Дарси установил, что при постоянном сопротивлении слоя песка [2,23]:

, (1)

где V -объем фильтрата, м3/с,

k — коэффициент фильтрации, зависящий от свойств грунта (величина обратная сопротивлению слоя), м3/(м2∙с),

F — площадь фильтрации, м2,

I — гидравлический уклон, равный потере напора D Н на пути L , м.

Приведённое соотношение аналогично известным для интенсивности перемещения тепла, вещества и является частным случаем закона, выражающего скорость процесса. Все рассмотренные далее более сложные уравнения фильтрования представляют собой по существу модификацию закона Дарси.

Фильтрование является гидродинамическим процессом, скорость которого прямо пропорциональна разности давлений, создаваемой по обеим сторонам фильтровальной перегородки (движущая сила процесса), и обратно пропорциональна сопротивлению, испытываемому жидкостью при ее движении через поры перегородки и слой образовавшегося осадка. Сопротивление при фильтровании является суммой сопротивления фильтровальной перегородки и слоя осадка.

В отечественной литературе традиционно уравнение фильтрования в дифференциальной форме может быть записано так:

, (2)

где V – объём фильтрата, м3,

F – поверхность фильтрования, м2,

t — продолжительность фильтрования, с,

— разность давлений, Па,

— вязкость жидкой фазы суспензии, Па·с,

— сопротивление слоя осадка, м-1,

— сопротивление фильтровальной перегородки, м-1.

При этом величина

где W представляет собой переменную скорость фильтрования, выраженную в м /с.

Разность давлений по обе стороны фильтровальной перегородки создают разными способами, в результате чего осуществляют различные процессы фильтрования.

Если пространство над суспензией сообщают с источником сжатого газа, или пространство под фильтровальной перегородкой присоединяют к источнику вакуума, то происходит процесс фильтрования при постоянной разности давлений, поскольку давление в ресиверах поддерживается постоянным. При этом скорость процесса уменьшается в связи с увеличением сопротивления слоя осадка возрастающей толщины.

Уравнение фильтрования при постоянной разности давлений:

, (4)

где x — отношение объёма осадка к объёму фильтрата,

— удельное сопротивление осадка (или слоя), м-2.

Для режима фильтрования при постоянной разности давлений продолжительность фильтрования пропорциональна квадрату объёма полученного фильтрата:

. (5)

Если суспензию подают на фильтр поршневым насосом, производительность которого при данном числе оборотов электродвигателя постоянна, то осуществляется процесс фильтрования при постоянной скорости, при этом разность давлений увеличивается вследствие уже упоминавшегося увеличения сопротивления осадка возрастающей толщины.

Для режима фильтрования при постоянной скорости перепад давления возрастает по мере увеличения продолжительности фильтрования:

. (6)

Если суспензию транспортируют на фильтр центробежным насосом, производительность которого при данном числе оборотов электродвигателя уменьшается при возрастании сопротивления осадка, что обусловливает повышение разности давлений, то производится процесс фильтрования при переменных разности давлений и скорости.

Независимо от того, каким образом создают разность давлений, движущая сила процесса фильтрования возрастает прямо пропорционально этой разности. Однако в большинстве случаев скорость фильтрования возрастает медленнее, чем увеличивается разность давлений, так как при увеличении последней поры перегородки и осадка сжимаются, и сопротивление возрастает.

Для осадка или фильтрующей перегородки постоянной толщины и с постоянной долей пустот в сечении — e , уравнение кинетики процесса фильтрования можно записать (в соответствии с законом Дарси) в следующем виде:

, (7)

где V -объем фильтрата, м3,

t — продолжительность фильтрования, с,

e — порозность слоя или осадка,

Ф — фактор формы, м2/м2,

Δ p — перепад давлений при фильтровании, Па.

m — вязкость фильтрата, Па ∙ с,

h ос -толщина осадка или слоя, м,

d – диаметр шара, имеющий тот же объем, что и частица,

Фактор формы Ф представляет собой отношение поверхности шара, имеющего такой же объем, что и частица неправильной формы, к действительной поверхности частицы.

Порозность выражает объём свободного пространства между частицами в единице объёма, занятого слоем:

, (8)

где — общий объём, занимаемый слоем, м3,

— объём, занимаемый самими частицами, образующими слой, м3

В реальных условиях порозность e осадка зависит от скорости осаждения частиц и от состояния поверхности, на которой происходит образование слоя осадка.

Большое влияние на ход процесса фильтрования оказывает начальная стадия – стадия образование осадка, т. к., во-первых, в начале процесса скорость образования фильтрата максимальна, во-вторых, повышенная скорость образования фильтрата может привести к быстрой закупорке пор фильтрующей перегородки и, следовательно, к быстрому увеличению сопротивления, в-третьих, характер образования начальных слоёв осадка может оказать значительное влияние на структуру всего слоя осадка.

Осадки могут быть сжимаемыми и несжимаемыми. Несжимаемые осадки и фильтрующие перегородки характеризуются принятым допущением: порозность их, а, следовательно, и сопротивление потоку жидкости в процессе фильтрования остаются постоянными.

Практически несжимаемых осадков не бывает, но к этой группе обычно относят осадки веществ минерального происхождения (песок, мел, сода и др.) с размером частиц больше 100 мкм, сопротивление слоя которых движущемуся потоку незначительно зависит от перепада давлений или скорости осаждения.

К несжимаемым перегородкам относятся пористые керамические или стеклянные, а также металлические фильтрующие перегородки. Сжимаемые осадки и перегородки характеризуются уменьшением порозности в результате образования более плотного осадка и увеличением сопротивления при повышении перепада давлений.

Для сильно сжимающихся осадков (гидроокиси железа, меди и др.) увеличение разности давлений сверх некоторого критического значения приводит к уменьшению скорости фильтрования.

В общем случае для образования несжимаемого осадка на несжимаемой фильтрующей перегородке (сопротивление которой пренебрежимо мало ) при e = const в уравнении (7) можно объединить постоянные величины, характеризующие свойства данного осадка:

. (9)

Тогда уравнение (7) примет вид:

(10)

. (11)

Таким образом, удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью 1 Па∙с фильтровалась со скоростью 1 м/с сквозь слой осадка толщиной 1 м.

Удельное сопротивление представляет собой сопротивление единицы объёма осадка высотой 1 м, отложенного на площади 1 м2, и может быть определено опытным путём.

Сопротивление всего слоя осадка можно выразить равенством:

. (12)

Толщину осадка h ос можно выразить с помощью объема фильтрата, учитывая пропорциональность объемов осадка и фильтра.

Так как сопротивление осадка пропорционально количеству отложившегося осадка, а следовательно, пропорционально количеству прошедшего фильтрата, то:

, (13)

где К – константа фильтрования, характеризующая режим процесса фильтрования и физико-химические свойства осадка и жидкости, м2/с.

Сопротивление фильтрующей перегородки включает сопротивление самой перегородки и сопротивление тонкого слоя осадка, оставшегося на перегородке.

В начальный момент фильтрования, когда на фильтровальной перегородке ещё не образовался слой осадка, из уравнения (2) получим:

. (14)

Это означает, что сопротивление фильтровальной перегородки численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью 1 Па·с проходила сквозь фильтровальную перегородку со скоростью 1 м/с.

Сопротивление фильтрующей перегородки можно заменить сопротивлением слоя осадка, оказывающего такое же сопротивление процессу фильтрования, какое оказывает фильтрующая перегородка, и выразить соответствующим количеством фильтрата С:

, (15)

где — константа фильтрования, характеризующая гидравлическое сопротивление фильтрующей перегородки, м3/м2.

Для режима фильтрования при постоянной разности давлений уравнение скорости фильтрования имеет вид:

, (16)

где .

После соответствующих преобразований получим параболический закон фильтрования:

( V + C )2 = K ∙ ( t + t 0 ), (17)

где t 0- продолжительность образования слоя осадка с сопротивлением, равным сопротивлению фильтрующей перегородки.

Рисунок 1 – Графическая зависимость V = f ( t )

Из рисунка 1 следует, что вершина кривой будет совпадать с началом координат лишь в том случае, когда кроме сопротивления осадка учитывается сопротивление фильтрующей перегородки. В начальный момент процесса, когда t =0, V =0, уравнение (17) примет вид:

Тогда для расчета производительности фильтрата или продолжительности фильтрования удобно использовать зависимость, получающуюся после раскрытия скобок в уравнении (17 ) и учёта уравнения (18)

V 2+2 V ∙ C = K ∙ t . (19)

Константы фильтрования С и К, необходимые для расчетов, определяются экспериментально. Замеряют объемы фильтрата V и время t , в течение которого собранны эти объемы, затем уравнение, связывающее скорость фильтрования dV / d t и продолжительность фильтрования t , может быть выражено прямой линией.

Так, дифференцируя уравнение (19), имеем:

(20)

. (21)

В уравнении (21) dV и d t представляют собой приращение объема, полученного фильтрата и времени фильтрования:

. (22)

Это уравнение изображается прямой линией ДМ (рисунок 2), наклоненной к оси абсцисс под углом a , тангенс которого tg a =2/К. Эта линия отсекает от оси ординат ( при V =0 ) отрезок В=2С/К. Для графического определения констант К и С на оси ординат откладывают величину, обратную скорости фильтрования d t / dV = D t / D V , а по оси абсцисс — объемы фильтрата, собранного с единицы поверхности фильтра (рисунок 2). Экстраполируют построенную по опытным точкам прямую до пересечения с абсциссой, находят величину константы С, равную отрезку ДО, а по тангенсу угла наклона прямой — величину К.

Рисунок 2 – Графическая зависимость

Опытные значения объемов фильтрата V 1 и V 2 за время t 1 и t 2 позволяют вычислить константы К и С с помощью уравнения (19), т. е., решая систему:

. (23)

Необходимо отметить, что уравнение (2) и все последующие связанные с ним соотношения применимы только к ламинарному течению жидкости в порах осадка. Такое допущение основано на том, что при малых размерах пор и скоростях течения числа Рейнольдса невелики.

Целью работы является определение констант процесса фильтрования, а также производительности фильтра по фильтрату.

4 ОПИСАНИЕ УСТАНОВКИ

Установка для проведения лабораторных работ по фильтрованию (рисунок 3) состоит из погружного элемента вакуум-фильтра (1), бачка с мешалкой (2) для суспензии, вакуум-насоса (8), приемника для фильтрата (3) и измерительных приборов: термометра (4), вакуумметра (5) и секундомера.

Элемент вакуум-фильтра разборный и состоит из воронки со съемной решеткой (дырчатым диском) и прижимной крышкой. На воронку с установленной решеткой накладывают фильтровальную ткань и зажимают крышкой.

Отдельные части установки соединены между собой трубопроводами и вакуумными резиновыми трубками. Имеется кран (6), которым при работающем вакуум-насосе создают нужный вакуум, и кран (7) или зажим, установленный между бачком для суспензии и приемником для фильтрата. Этот кран открывают после подготовки всей установки к работе на заданном режиме.

5 МЕТОДИКА ПРОВЕДЕНИЯ РАБОТЫ

Приготавливают суспензию (или пользуются готовой суспензией) и заливают в бак (2) – рисунок 3. Суспензию готовят в отношениях Т:Ж=1:1000. Во избежание уплотнения осадка (мел или другой материал) включают мешалку.

Собирают вакуум-фильтр (1) и устанавливают его в баке (2), погружая в суспензию на несколько сантиметров. Зажим или кран (7) закрыт, кран (9) вначале открыт. Включают вакуум-насос и, осторожно закрывая кран (9), устанавливают заданный руководителем вакуум по вакуумметру (5). После установления рабочего режима открывают кран (7) и одновременно включают секундомер.

1 — вакуум-фильтр; 2 — бачок с мешалкой; 3 — приемник для фильтра; 4 — термометр; 5 — вакуумметр; 6,7,9 — краны; 8 — вакуум-насос.

Рисунок 3 – Схема лабораторной установки

Первый замер времени делают при появлении первых капель фильтрата в приемнике. Через некоторое время, когда в приемнике наберется некоторое количество фильтрата, производят, не выключая секундомер, одновременный замер времени и собранного фильтрата. Такие замеры производят 5…6 раз до окончания фильтрования, которое замечают по замедленному выходу фильтрата.

После этого, не выключая вакуум-насоса, закрывают кран (6) и выключают секундомер, записав время и объем фильтрата. Затем освобождают вакуум-фильтр (2) и поднимают его вверх так, чтобы резиновая трубка не создавала застоев жидкости.

Фильтрующая поверхность фильтра должна быть повернута вверх. После этого открывают кран (6).

Начинается второй этап работы — продувка фильтра, просушка осадка. Когда поверхность потеряет влажный блеск и перестанет изменять свой вид, продувку прекращают, выключают вакуум-насос. Добавившимся при продувке количеством фильтрата пренебрегаем из-за его малости.

Фильтр разбирают, осадок снимают в специальную емкость, после этого промывают фильтр и ткань, и собирают фильтр снова. Результаты замеров заносят в таблицу.

6 ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

По полученным замерам объемов V 1, V 2. Vn и времени t 1, t 2. t n, рассчитывают удельный объем фильтрата V=V/Fф, собранный с единицы поверхности фильтра, определяют разности D t и D V и вычисляют величины, обратные скорости фильтрования D t 1 / D V1, D t 2 / D V2 . D t n/ D Vn. Затем строят график, откладывая по оси абсцисс величины удельных объемов от V1, до V2, а по оси ординат величины отношения от D t 1 / D V1, до D t п / D Vп. Так как отношение D t / D V является средней величиной для соответствующих интервалов D V, то величины этих отношений следует откладывать по вертикали из середины однозначных интервалов либо, проводя прямую через середины отрезков а1- b 1, а2- b 2, и т. д., (см. рисунок 2), как об этом сказано выше.

Для определения константы К находим тангенс угла наклона прямой ДМ (рисунок 2) как отношение катетов, взятых в соответствующих масштабах. Например:

. (24)

Из выражения tg a = 2/К находим константу фильтрования К:

Константу С находим непосредственно замером отрезка ДО (см. рисунок 2). Так определяем графические константы процесса фильтрования.

Расчётные константы процесса фильтрования из опытных данных определяем, решая систему уравнений (23) по двум парам значений удельных объёмов и времени.

Далее определяют скорости фильтрования в начальный и конечный момент времени: и :