Одним из главных аспектов современного урока, согласно требованиям ФГОС ООО, является деятельностный аспект. Применение деятельностного подхода в обучении математике обеспечивает развитие у школьников основной школы высокого уровня знаний, умений, приемов мышления, которые в свою очередь способствуют повышению качества обучения.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Скачать:

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Предварительный просмотр:

Тема: Уравнение прямой вида y = kx + l.

1. Предметные: знать геометрический смысл коэффициентов к и l в уравнении прямой у = кх + l, уметь по уравнению прямой определять взаимное расположение графиков
2. Метапредметные: развивать навыки исследовательской работы, систематизации и обобщения, формировать умение четко и ясно излагать мысли.
3. Личностные: развитие личности учащихся на основе универсальных учебных действий: формировать учебно-познавательный интерес к предмету, готовность и способность к саморазвитию, умение оценивать свою работу, навыки сотрудничества

Материально-техническое обеспечение урока:

презентация к уроку, задания для групп с исследовательской работой (приложение 1),

материалы для домашней работы (приложение 2)

Методы организации работы:

1. создание проблемной ситуации
2. организация исследовательской деятельности
3. метод рефлексивной самоорганизации (деятельностный метод)

Приветствие, эмоциональный настрой.

На доске написаны слова : « Скажи мне – и я забуду, покажи мне – и я запомню, дай сделать – и я пойму»

1. Проверка уровня усвоения изученного материала, готовности к работе на уроке. Актуализация опорных знаний (презентация):

Какое уравнение называется линейным уравнением с двумя переменными?

Уравнение вида ax +by=c, где a, b,c – некоторые числа, а х, у – переменные.

Что является решением линейного уравнения с двумя переменными?

Пара чисел (х ; у), которая обращает уравнение в верное равенство.

Что является графиком линейного уравнения с двумя переменными?

Графиком является прямая.

Как из уравнения вида ax +by=c получить уравнение вида у=kx + l?

Решить уравнение относительно переменной у.

Что является графиком уравнения у = kх ?

Графиком является прямая, проходящая через начало координат.

В каких координатных четвертях расположен график прямой у=kx ,

если k > 0? ( График расположен в 1 и 3 координатных четвертях)

Что является графиком уравнения у = l?

Графиком является прямая, параллельная оси Х и проходящая через точку c координатами (0, l).

Слайд №8: На чертеже изображены три прямые. Каждой прямой поставить в соответствии уравнение: 1) у = 1,5х 2) у = 1,5 3) у = — 1,5х

Запишите уравнение прямой, параллельной прямой у = 0,5 х + 2 и проходящей через точку (4; — 1).

2. Актуализация и фиксирование затруднения в поставленной задаче (проблемная ситуация). (4-5 мин)

Готовы ли мы выполнить такое задание? Достаточно ли знаем? Как вы думаете, от чего зависит расположение прямой в координатной плоскости? (от коэффициентов)

3. Постановка учебной задачи: выясним, как влияют коэффициенты на взаимное расположение прямых в координатной плоскости. Цели для учеников:

1. знать геометрический смысл коэффициентов k и l в уравнении прямой

2. уметь по уравнению прямых определять взаимное расположение графиков

4. Проведем исследовательскую работу (работа выполняется по группам в программе УМК «Живая математика»). Для каждой группы приготовлены карточки для исследовательской работы (приложение 1).

Выясним, какую роль играет коэффициент k

1 группа: Построить в одной и той же координатной плоскости прямые у = 3х,

у = 3х + 3 и у = 3х — 4

2 группа: Построить в одной и той же координатной плоскости прямые у = — 3х,

у = — 3х +3 и у = -3х — 1

3 группа: Построить в одной и той же координатной плоскости прямые у = 2х,

у = 2х + 3 и у = 2х- 3

Что общего у уравнений? Что общего у прямых, являющихся графиками этих уравнений? После построения ученики в группах обсуждают полученный результат, формулируют свои выводы, один человек от группы выступает с отчетом о работе.

1. если коэффициенты k равны, то прямые параллельны

2. если k > 0, то угол острый, а если k

k — угловой коэффициент прямой.

Если угловые коэффициенты одинаковы, то прямые параллельны.

Если же угловые коэффициенты различны, то прямые пересекаются.

Если k > 0, то угол наклона к положительному направлению оси Х — острый, а если k

Выясним, какую роль играет коэффициент l .

Проведем аналогичную исследовательскую работу.

1 группа: Построить в одной и той же координатной плоскости прямые у = 2 у = 2х + 2 и у = — х +2

2 группа: Построить в одной и той же координатной плоскости прямые у = — 2,

у = х – 2 и у = -2х — 2

3 группа: Построить в одной и той же координатной плоскости прямые у = 4, у = 0,6х + 4 и у = -3х + 4

Что общего у уравнений? Что общего у прямых, являющихся графиками этих уравнений?

Проводится аналогичная работа в группах.

После исследования делаем выводы: в каждом случае мы получили пучок прямых, приходящих через точку (0; l).

Прямая y = kx + l пересекает ось у в точке (0; l)

Если l >0 , то точка пересечения расположена выше оси Х

Учитель: Итак, посмотрите, сколько полезной информации мы можем извлечь из уравнения прямой: Коэффициенты k и l позволяют судить о положении прямой в координатной плоскости: коэффициент к определяет угол наклона прямой к положительному направлению оси ох, а коэффициент l показывает, в какой точке прямая пересекает ось у.

1. Первичное закрепление: задания выполняются устно, с пояснениями и комментариями..

1. Для каждой прямой назвать угловой коэффициент и точку пересечения с осью Y. а) у = х + 7 б) у = -0,4х + 3 в) у = 2,4х — 5 г) у = 6 — 3х

2. Запишите уравнение прямой, если известен ее угловой коэффициент k и точка, в которой эта прямая пересекает ось у:

а) k = 2, А(0,1) б) к = — 4, А(0, -0,5) в) к = -0,5, А(0;0)

3. На доске схематично показать расположение в координатной плоскости прямой, заданной уравнением у = 3,2х — 3 у = 3,2х + 4 у = 0,6х -3 у = -2х +4 (первую — учитель с пояснениями, дальше по одной ученики с комментарием)

6. Включение в систему знаний, разрешение проблемной ситуации . (возвращаемся к задаче из ГИА): Запишите уравнение прямой, параллельной прямой у = 0,5 х + 2 и проходящей через точку (4; — 1).

1. k = 0,5 , т.к. прямые параллельны у = 0,5х + l
2. прямая проходит через точку (4;-1), значит -1 = 0,5· 4 + l, l = -3
3. у = 0,5х -3

1. Самостоятельная работа с самопроверкой и коррекция.

1. Отметьте пары параллельных прямых.

а) y = 2х – 3 и у = 3х – 2

б) y = 5х – 2 и у = 5х — 4

в) y = 4х – 3 и у = -4х +3

г) y = -2х – 3 и у = 3 -2х

1. Назовите координаты точки в которой прямая y=-5x+4 пересекает ось Оу.
2. Дана прямая у = — 4х + 3. Запишите уравнение какой-нибудь прямой:

а) имеющей такую же точку пересечения с осью у;

б) имеющей такой же угловой коэффициент.

4) Изобразить схематически на координатной плоскости прямые:

а) у= 3х- 2 б) у = 3х +2 в) у=3х г) у = — 2

8. Рефлексия учебной деятельности на уроке (итог урока):

Слайд № 19 – изображение дерева

Если вы считаете, что вы поняли тему сегодняшнего урока, то наклейте зеленый листочек на дерево.

Если вы считаете, что не достаточно усвоили материал, то наклейте желтый листочек на дерево.

Если вы считаете, что вы не поняли тему сегодняшнего урока, то наклейте красный листочек на дерево.

Я увижу цветовой индекс урока.

Ученики наклеивают листочек нужного цвета.

9. Домашнее задание:

1. придумать и решить 3 различных задачи, аналогичных тем, которые выполняли на уроке, записать их для взаимообмена заданиями.
2. Сделать кластер по теме урока (материалы для кластера выдаются каждому)- приложение 2.

Карточка для выполнения исследовательской работы

1 часть «Коэффициент k»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = 3х; у = 3х + 3; у = 3х – 4

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент k > 0, то прямая и положительное направление оси Х образуют ______________________ угол;

Если коэффициент k

2 часть «Коэффициент l»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = 2; у = — 2х + 2; у = x +2

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент l > 0, то точка пересечения располагается _______ оХ;

Если коэффициент l

1 часть «Коэффициент k»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = — 3х; у = — 3х + 3; у = — 3х – 2

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент k > 0, то прямая и положительное направление оси Х образуют ______________________ угол;

Если коэффициент k

2 часть «Коэффициент l»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = — 2; у = — 2х — 2; у = x — 2

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент l > 0, то точка пересечения располагается _______ оХ;

Если коэффициент l

1 часть «Коэффициент k»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = 2х; у = 2х + 3; у = 2х – 2

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент k > 0, то прямая и положительное направление оси Х образуют ______________________ угол;

Если коэффициент k

2 часть «Коэффициент l»

1. Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:

у = 4; у = 0,6х + 4; у = — 3 x + 4

1. Заполнить таблицу:

Как располагаются прямые

Если у прямых равны коэффициенты ______, а коэффициенты ______ различны, то прямые _____________________________________.

Если коэффициент l > 0, то точка пересечения располагается _______ оХ;

Если коэффициент l

Материалы для домашней работы (составление кластера)

Заполни схему, используя нужные материалы из таблицы:

k — угловой коэффициент прямой. Если угловые коэффициенты одинаковы, то прямые параллельны. Если же угловые коэффициенты различны, то прямые пересекаются.

Прямая y = kx + l пересекает ось у в точке (0; l)

Если l >0, то точка пересечения находится выше оси Х;

Если угловой коэффициент

то прямая y = l параллельна оси Х и проходит через точку с координатами

то прямая y = kx проходит через начало координат

расположена в 1 и 3 координатных четвертях, если k>0;

расположена в 2 и 4 координатных четвертях, если k

Если точка (х; у) принадлежит графику уравнения ах + ву = с, то пара чисел (х;у) является решением этого уравнения

Уравнение ах + ву =с имеет множество решений вида (х;у)

Предварительный просмотр:

Видео:Угловой коэффициент прямойСкачать

Подписи к слайдам:

Уравнение прямой вида у=кх+ l у у у х х х

Прямая у = кх + l Скажи мне – и я забуду, покажи мне – и я запомню, дай сделать – и я пойму

Прямая у = кх + l На чертеже изображены три прямые. Каждой прямой поставить в соответствии уравнение: 1) у = 1,5х 2) у = 1,5 3) у = — 1,5х

Прямая у = кх + l БЛИЦ-ОПРОС 1. Выразить переменную у из линейного уравнения 4х — 10у = 3. 2. Принадлежат ли точки А(-2;7) и В(6; 9), прямой, заданной уравнением у = -2х + 3 3. При каком значении в прямая 0,5х + в у = 8 проходит через точку Е(-14; 5).

Прямая у = кх + l Ответы 1. у = 0,4х — 0,3 2 . 3. в = -3 А(-2;7) В(6; 9) 7 = -2 * (-2) + 3 9 = -2 * 6 + 3 7=7 9 = -9 принадлежит не принадлежит

Прямая у = кх + l Запишите уравнение прямой, параллельной прямой у = 0,5 х + 2 и проходящей через точку (4; — 1).

Прямая у = кх + l Задачи: выяснить, как влияют коэффициенты на взаимное расположение прямых в координатной плоскости. Цели : знать геометрический смысл коэффициентов k и l в уравнении прямой у = k х+ l , уметь по уравнению прямых определять взаимное расположение графиков

Прямая у = кх + l исследовательская работа

Прямая у = кх + l 1 группа 3 группа 5 группа у = 3х у = — 3х у = 0.5х у = 3х + 3 у = — 3х +3 у = 0,5х +3 у = 3х – 4 у = — 3х – 2 у = 0,5х – 2 2 группа 4 группа у = 2 у = — 2 у = — 2 х + 2 у = — 2 х — 2 у = x +2 у = x — 2

Прямая у = кх + l k — угловой коэффициент прямой. Если угловые коэффициенты одинаковы, то прямые параллельны. Если же угловые коэффициенты различны, то прямые пересекаются. Если k > 0, то угол наклона к положительному направлению оси Х — острый, а если k 0 , то точка пересечения расположена выше оси Х Если l 0, l 0, l >0 В) k Мне нравится

Видео:Угловой коэффициент прямой. Решение задач.Скачать

Конспект урока «Угловой коэффициент прямой» (с подготовкой к ОГЭ)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

План-конспект урока по геометрии «Уравнение прямой. Угловой коэффициент прямой»

Усольцева Мария Николаевна, учитель математики

Тип урока: открытие нового знания .

— вывести уравнение прямой и показать, как можно использовать это уравнение при решении геометрических задач;

-совершенствовать навыки решения задач методом координат;

-содействовать в ходе урока воспитанию решительности, смелости при выполнении заданий, самостоятельности;

-развитие памяти, логического мышления обучающихся при решении задач.

Знать: формулы уравнений окружности и прямой и уметь их применять

5-минутка ОГЭ (работа у доски):

(Березина А.)

(Лебедев К.)

(Астраханцев Е.)

II .Актуализация опорных знаний (5 мин):

1. Какой вид принимает уравнение окружности в прямоугольной системе координат?

(x-x₀) 2 + (y-y₀) 2 = R 2 или (x-a) 2 + (y-b) 2 = r 2

2.Какие координаты в данном случае имеет центр окружности?

3.Какой вид примет уравнение окружности, если ее центр имеет координаты (0; 0)?

4.Представлено уравнение окружности ( x -5) 2 + ( y +8) 2 = 49. Найти центр окружности, её радиус и диаметр.

О (5; -8)- центр окружности

A (1;2): 1+4 ≠ 25- не лежит;

B (3;4): 9+16 = 25- лежит;

C (0;5): 0+25 = 25 –лежит;

D (5;-1): 25+1 ≠ 25 не лежит.

Уравнение вида называется уравнением прямой, где

a , b , c – числа, причем одновременно не обращаются в ноль, x , y — переменные)

Выразим из этого уравнения y , получаем:

by= — ax –c | : b , (b≠0)

y = x

= k

= d

III . Изучение нового материала (10 мин):

k — угловой коэффициент прямой (тангенс угла наклона прямой). k = tgα

Угол наклона прямой- это угол между данной прямой и положительной полуосью х.

Если α – острый угол, то k > 0, прямая проходит через I и III координатные четверти

I

y= kx +d

α

Если α – тупой угол, то k II и IV координатные четверти

II

α

ax + by + c = 0 , x =0

by + c = 0 – уравнение прямой || оси ox

by+ c = 0

ax + by + c = 0 , y =0

ax + c = 0 – уравнение прямой || оси oy

ax + c = 0

№387,388,390,391,393 (у доски: Архипов А., Верхоланцева Ю., Французов Д., Крапивин Н., Хлюпин И.)

Дополнительное задание для высокомотивированных обучающихся: №395,397 (Верхоланцева Ю., Березина А.).

V. Подготовка к ОГЭ (интеграция с предметом алгебра ) (7 мин):

1. С чем мы сегодня познакомились на уроке?

С уравнением прямой.

2. Какой вид принимает уравнение прямой?

3.Как определить через какие четверти проходит прямая, на что нужно обратить внимание?

На коэффициент k , если k >0, то через I и III четверти ;

если k II и IV четверти.

4. Что такое угол наклона прямой?

Угол наклона прямой- это угол между данной прямой и положительной полуосью х.

5. Какое уравнение имеет прямая параллельная оси ОХ, ОУ?

— Какие задания вызвали у вас затруднения?

— Какие нужно еще рассмотреть подробнее?

— Что показалось легким?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:УЧИМСЯ ПОНИМАТЬ ЛИНЕЙНУЮ ФУНКЦИЮ. Уравнения прямой с угловым коэффициентом, по точкам и в отрезкахСкачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 575 647 материалов в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 11. Угловой коэффициент прямой

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 02.02.2021
• 330
• 18

• 02.02.2021
• 219
• 4

• 02.02.2021
• 163
• 2

• 02.02.2021
• 385
• 6

• 02.02.2021
• 107
• 2

• 02.02.2021
• 477
• 58

• 02.02.2021
• 739
• 25

• 02.02.2021
• 210
• 9

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 02.02.2021 1056
• DOCX 835.8 кбайт
• 121 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Усольцева Мария Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 2 месяца
• Подписчики: 1
• Всего просмотров: 92014
• Всего материалов: 54

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Уравнение прямой с угловым коэффициентомСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Урок 6

уравнение Прямой с угловым коэффициентом.

уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.

уравнение Прямой, Проходящей через две данные точки.

Уравнение Прямой с угловым коэффициентом.

Пусть дана некоторая Прямая, не ПерПендикулярная оси ох. назовем углом наклона данной Прямой к оси ох угол а, на который нужно Повернуть ось ох, чтобы Положительное наПравление совПало с одним из наПравлений Прямой. угол а может Принимать различные значения, которые отличаются друг от друга на величину ± NП, где N — натуральное число. как Правило, в качестве угла наклона берут наименьшее неотрицательное значение угла а, на который нужно Повернуть (Против часовой стрелки) ось ох, чтобы ее Положительное наПравление совПало с одним из наПравлений Прямой. в этом случае 0

Тангенс угла наклона Прямой к оси ох называют угловым коэффициентом этой Прямой и обозначают буквой k: k= tgа (1) . из данного равенства следует, что если а=0, т.е. Прямая Параллельна оси ох, то k=0. если а=П/2, т.е. Прямая ПерПендикулярна к оси ох, то выражение k= tgа теряет смысл. в таком случае говорят, что угловой коэффициент «обращается в бесконечность».

Выведем уравнение данной Прямой, если известны ее угловой коэффициент k и величина b отрезка ов, который она отсекает на оси оу.

Пусть м — Произвольная точка Плоскости с координатами х и у. Проведем Прямые вN и Nм, Параллельные координатным осям, и Получим Прямоугольный треугольник вNм.

точка м лежит на Прямой тогда и только тогда, когда величины Nм и вN удовлетворяют условию: Nм / вN =tgа .

но Nм=см-сN=см-ов=у-b, вN=х. отсюда, учитывая формулу (1), Получаем, что точка м(х;у) лежит на данной Прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению (у-b) / х=k, которое После Преобразований Примет вид у=kх+b (2) .

уравнение (2) называют уравнением Прямой с угловым коэффициентом . если k=0, то Прямая Параллельна оси ох и ее уравнение имеет вид у=b.

итак, уравнение любой Прямой, не ПерПендикулярной оси ох, имеет вид (2). очевидно, верно и обратное: любое уравнение вида (2) оПределяет Прямую, имеющую угловой коэффициент k и отсекающую на оси оу отрезок, величина которого b.

Пример 1 . составить уравнение Прямой, отсекающей на оси оу отрезок b=3 и образующий с осью ох угол а=п/4.

Решение. находим угловой коэффициент: k= tgа = tgа/ 4=1. Подставив k и b в равенство (2), Получим искомое уравнение Прямой: у=1х+3 или у-х-3=0.

Пример 2. Построить Прямую, заданную уравнением у=0,75х+2.

решение. отложим на оси оу отрезок ов, величина которого равна 2, Проведем через точку в Параллельно оси ох отрезок, величина которого вN=4, и через точку N Параллельно оси оу отрезок, величина которого Nм=3 (т.к. 0,75=3 / 4).

После этого Проводим Прямую вм, которая и является искомой. она имеет данный угловой коэффициент k=0,75=3 /4 и отсекает на оси оу отрезок величины b=2.

Уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.

в ряде случаев возникает необходимость составить уравнение Прямой, зная одну ее точку м 1 (х 1 ;у 1 ) и угловой коэффициент k . заПишем уравнение Прямой в виде (2), где b – Пока не известное число. так как Прямая Проходит через точку м 1 (х 1 ;у 1 ), то координаты этой точки удовлетворяют уравнению (2): у 1 = k х 1 + b . выразим из этого равенства b и Подставим его в уравнение (2), Получим искомое уравнение: у-у 1 = k (х – х 1 ) (3).

замечание. если Прямая Проходит ПерПендикулярно оси ох, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение имеет вид х – х 1 =0. формально это уравнение можно Получить из уравнения (3), если разделить обе части уравнения (3) на k и затем устремить k к бесконечности.

Пример 3. составить уравнение Прямой, Проходящей через точку м(2;1) и образующий с осью ох угол а=45 0 .

решение. найдем угловой коэффициент: k = tgа = tg 45 0 =1. Подставим координаты точки м и значение углового коэффициента k в равенство (3), Получим уравнение Прямой: у-1=х-2 или у-х+1=0.

уравнение Прямой, Проходящей через две данные точки.

Пусть даны две точки м 1 (х 1 ;у 1 ) и м 2 (х 2 ;у 2 ). Приняв в уравнении (3) точку м(х;у) за м 2 (х 2 ;у 2 ), имеем у 2 – у 1 = k (х 2 – х 1 ). выразим из Последнего равенства k и Подставим его в уравнение (3), Получаем искомое уравнение:

это уравнение При условии, что у 1 не равен у 2 , можно заПисать так: (4)

если у 1 =у 2 , то уравнение искомой Прямой имеет вид у=у 1 . в этом случае Прямая Параллельна оси ох. если х 1 =х 2 , то Прямая Параллельна оси оу и ее уравнение имеет вид х=х 1 .

Пример 4. составить уравнение Прямой, Проходящей через точки а(3;1) и в(5;4).

решение. Подставив координаты точек а и в в равенство (4), Получаем искомое уравнение Прямой: = или 3х – 2у – 7 =0.

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области

🔥 Видео

9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой на плоскостиСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Урок 5. Уравнение прямой с угловым коэффициентом. Декартовы координаты. Геометрия 9 класс.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

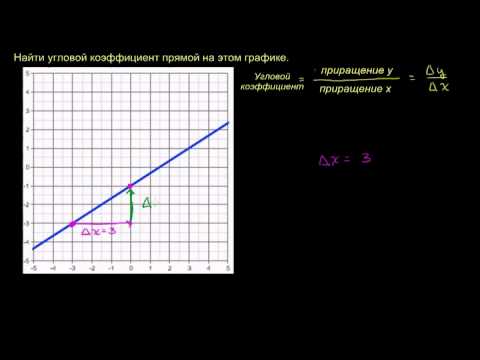
Угловой коэффициент прямой. Пример 1Скачать

Видеоурок "Общее уравнение прямой"Скачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Угловой коэффициент прямойСкачать

Уравнение прямой. Урок 6. Геометрия 9 классСкачать