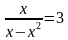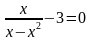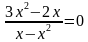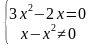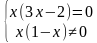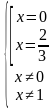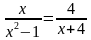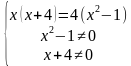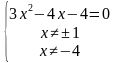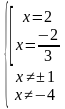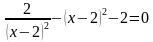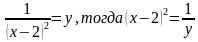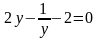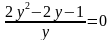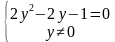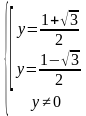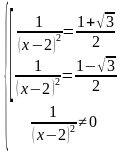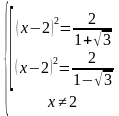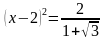Урок №10. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.
- Просмотр содержимого документа «Повторение. Рациональные уравнения и неравенства»
- Конспект урока по математике «Решение рациональных уравнений и неравенств»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Урок в 10 классе «Рациональные уравнения». методическая разработка по алгебре (10 класс) по теме
- Скачать:
- Предварительный просмотр:
- 🎥 Видео
Просмотр содержимого документа
«Повторение. Рациональные уравнения и неравенства»
Тема урока: Повторение. Рациональные уравнения и неравенства
Цели: обобщить и систематизировать знания учащихся по теме.
Откройте тетради и запишите сегодняшнее число и тему урока. Записываем решение только тех примеров, которые вызывают у вас затруднение при решении.
Пример 1. Решить уравнение:
Решение. Приведем данное уравнение к стандартному виду, перенеся 3 в левую часть:
Приведем к общему знаменателю, приведем подобные члены и получим уравнение:
Решение данного уравнения запишем через систему:
Вынесем за скобки общий множитель:
Получим следующее решение:
Учитывая ОДЗ, получим ответ: 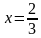
Пример 2. Решить уравнение:
Решение. Распишем данное уравнение, применяя основное свойство пропорции, и учтем ОДЗ:
В первом уравнении системы раскроем скобки, перенесем всё в левую часть, приведем подобные. Второе и третье задают ОДЗ, их тоже решим:

Решаем квадратное уравнение:
Оба корня подходят по ОДЗ.
Ответ: 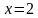
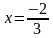
Пример 3. Решить уравнение:
Решение. Введем замену:
Получим уравнение относительно новой переменной следующего вида:
Приведем его к общему знаменателю:
Получили дробно-рациональное уравнение общего вида. Распишем его решение с помощью системы:
Решим квадратное уравнение, получим корни:
Вернемся к замене:
Применим свойство пропорции, получим:
Рассмотрим первое уравнение:
Правая часть больше 0, значит можем извлечь корень квадратный из обеих частей уравнения:
Тогда решением будет:
Рассмотрим второе уравнение:
Его правая часть меньше нуля, значит оно решений не имеет (квадрат не может быть отрицательным).
Пример 4. Решить неравенство
Решение. Найдем ОДЗ. В знаменателе корень четной степени, значит подкоренное выражение строго больше 0:
Так как знаменатель всегда положителен, перепишем неравенство в виде:
Применим формулу кубов к выражению и перепишем неравенство:
Вынесем общий множитель за скобку:
Решим данное неравенство методом интервалов, нанеся точки -1, 0, 1, и ОДЗ:
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: решить уравнение и неравенство
Видео:Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Конспект урока по математике «Решение рациональных уравнений и неравенств»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Тема : Решение рациональных уравнений и неравенств.
Обучающая: — интегрируя знания студентов по решению уравнений, добиться понимания сущности нахождения решения линейного уравнение, квадратного или любых уравнений, приводимых к квадратному, а также неравенств;
Развивающая :- выработать навыки применения теоретических знаний в решение подобных уравнений
Воспитательная :- добиваться осознанности в выполнении данного задания;
— формировать правильность мышления;
— побуждать к познавательной творческой деятельности на уроках математики.
Вид урока : изучение нового материала
Тип урока : Интерактивный урок с элементами проблемных ситуаций.
Элементы — развивающего обучения;
педагогических — Личностно-ориентированного обучения;
технологий : — технология работы в команде;
Межпредметные связи : химия ,техническая механика, электротехника.
Вступительное слово преподавателя.
Фронтальная беседа со студентами.
Подготовка студентов к активному и сознательному усвоению знаний.
Устный счет (вид работы решение 5 простейших уравнений).
Выражение известной величины из формул по физике, химии, электротехники,технической механике (выработка навыков межпредметных связей).
Спрашивайте – отвечаю (работа по алгоритму).
Работа в группах .
Подведение итогов . Домашнее задание.
Решение линейных, квадратичных уравнений и уравнений, приводимых к квадратному, широко используется при изучение учебных дисциплин «Физика», «Химия», «Техническая механика» и «Электротехника» .
Поэтому всем вам необходимо овладеть умением решения рациональных уравнений.
Ответить на вопросы :
Какое равенство называется уравнением ?
Какое уравнение называется квадратным ?
Что означает решить уравнение ?
Формула нахождения дискриминанта ?
Какие уравнения называются неполными ?
В каком случае квадратное уравнение имеет два корня?
В каком случае квадратное уравнение имеет один корень?
В каком случае квадратное уравнение не имеет корней?
Устный счет (вывести на экран задание)
Верно ли записано равенство ?
В конце устного счета обратить внимание, что линейные уравнения могут иметь один корень, не иметь корней или иметь их бесчисленное множество.
Квадратные уравнения могут иметь два корня различные, два корня одинаковые, не иметь корней.
Выразить неизвестное из формулы :
На экран выведены образцы выполнения заданий. Все студенты разбиваются на две группы: «сильные» и «слабые».
Задание для сильных студентов
Решить уравнения и неравенства.
1)=625 1)=27 1)27+ x 3=0 1) — 81 x =0
2) 2-128=0 2)-19+48=0 2)2=1 2) =16
3) -9=0 3)-25 x =0 3)- 4- 45=0 3) – 27 = 0
Задания для слабых учащихся
(тестовые задания с выбором ответа под номером задания соответствующую букву из предлагаемых ответов)
1.Верно ли решено уравнение: 1. Верно ли решено уравнение:
2(3 x – 7) – 1(9 x +11) = 4(3 – x ); 3(4 x – 3) – 2(5 – 2 x ) = 2(3 x – 4)
6 x – 14 – 9 x – 11 =12 — 4 x 12 x – 9 – 10+4 x =6 x -8
6 x – 9 x +4 x =12+14+11 12 x +4 x – 6 x = 9+10 — 8
Ответ: x =37 Ответ: x =1,1
и)да л)нет з)да и)нет
2. Решите уравнение 2. Решите уравнение
25 x – 17 =4 x – 5 – 13 x +14 +34 x 13 x – 15=3 x – 5 – 6 x +7+16 x
О) x =1; н) x — любое число; а) х=1; б)х-любое число ; в) корней нет.
Л) корней нет 3. Решите уравнение 4 x +4( x – 2) = 16
3. Решите уравнение 5 x +3( x +4)=20 д) х=3; е) х=2; к) корней нет.
О) х=1; п) х=-1 р) ч — любое число 4. Решите уравнение
4.Решите уравнение 6(1,2 x – 0,5) – 1,3 x = 5,9 x – 3.
6(1,2 x – 0,5) – 1,3 x = 5,9 x – 3. О) х=4; р) х- любое число; е) корней нет
К) х=5; л) корней нет; о) х — любое число 5. Верно ли раскрыты скобки?
5. Верно ли раскрыты скобки? (4 x – 1)( x +5) = 4 +20 x — 5.
(3 x +2)( x – 1) = – 3 x +2 x – 2 о) да; л) нет.
Т) да; ч) нет. 6. Решите уравнение
6. Решите уравнение ( x +3)( x – 7) = – 53. ( x +4)( x – 5) = – 26.
Н) х=8; о) х=2; т) х-любое число. Н) х=16; о) x =6; p ) x =0.
5. Работа в группах
Для работы в группах можно выполнить на доске то задание , с которым не справилось большинство студентов.
6. не рациональные уравнения
1) уравнение вида =0, где и Q — многочлены
+ x ≠0 2 x +5-2 x -2-3=0
6 . Подведение итогов
7. Домашнее задание
в ) (x -2)(x – 5)(x – 12)>0
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 574 134 материала в базе
Другие материалы
- 30.07.2020
- 144
- 3
- 30.07.2020
- 7096
- 191
- 30.07.2020
- 278
- 5
- 30.07.2020
- 249
- 7
- 30.07.2020
- 205
- 8
- 30.07.2020
- 209
- 2
- 30.07.2020
- 129
- 0
- 30.07.2020
- 176
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.07.2020 358
- DOCX 30 кбайт
- 23 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Хайбулаева Разият Набигулаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 6 месяцев
- Подписчики: 0
- Всего просмотров: 650
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
В России действуют более 3,5 тысячи студенческих отрядов
Время чтения: 2 минуты
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:✓ Метод интервалов. Рациональные уравнения и неравенства | Борис ТрушинСкачать

Урок в 10 классе «Рациональные уравнения».
методическая разработка по алгебре (10 класс) по теме
Данный урок предназначен для изучения темы в 10 классе: «Рациональные уравнения.» Тип урока: урок- лекция.
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Данный урок предназначен для изучения темы в 10 классе: «Рациональные уравнения.» Тип урока: урок- лекция. | 166 КБ |
| 10 класс: «Рациональные уравнения.» | 209.5 КБ |
Видео:Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Предварительный просмотр:
МОУ «Гимназия № 5 г. Белгорода»
Тема урока: Рациональные уравнения.
УМК : Алгебра и начала анализа: учеб. Для 10кл. общеобразоват. учреждений/[С.М.Никольский, М.К. Потапов.].-5-е изд., доп.-М.: Просвещение , 2006.-432с. Стр.65-74., 45-47.
Образовательная: систематизировать и обобщить известные из основной школы сведения о рациональных выражениях; показать способы решения рациональных уравнений;
Развивающая: расширить и углубить изучение различных видов рациональных уравнений разнообразными методами.
Воспитывающая: показать значимость изучаемой темы в разделе математика.
Тип урока: урок- лекция.
- Постановка цели урока (1мин).
- Подготовка к изучению нового материала(2 мин).
- 3.Ознакомление с новым материалом(38мин).
- 4.Итог урока.(2 мин)
- 5.Домашнее задание (2 мин)
Оборудование урока: интерактивная доска, проектор, компьютер.
1. Рациональные выражения.
2. Рациональные уравнения.
3.Системы рациональных уравнений.
Алгебра возникла из решения практических задач с помощью уравнений. Цели алгебры оставались неизменными на протяжении тысячелетий- решались уравнения: сначала линейные, потом квадратные, а там и уравнения еще больших степеней. Но форма, в которой излагались алгебраические результаты, менялись до неузнаваемости.
Уравнение- это самая распространенная форма математической задачи. Учение об уравнениях является главным содержанием школьного курса алгебры. Для решения уравнений нужно уметь производить действия над одночленами, многочленами алгебраическими дробями, уметь производить разложение на множители, раскрывать скобки и т. д. Нужно привести свои знания в порядок. Мы начнем повторение с понятия «рациональные выражения». Сообщение ученика о рациональных выражениях известных из основной школы. Таким образом, учение об уравнениях невозможно без учения о законах действий.
II. Основная часть.
Главное в понятии уравнения – это постановка вопроса о его решении. Уравнение, левая и правая части которого есть рациональные выражения относительно х, называют рациональным уравнением с неизвестным х.
Например, уравнения 5х 6 — 9х 5 + 4х — Зх + 1 = 0, являются рациональными.
Корнем (или решением) уравнения с неизвестным х называют число, при подстановке которого в уравнение вместо х получается верное числовое равенство.
Решить уравнение — значит найти все его корни или показать, что их нет. При решении рациональных уравнений приходится умножать и делить обе части уравнения на не равное нулю число, переносить члены уравнения из одной части в другую, применять правила сложения и вычитания алгебраических дробей. В результате будет получаться уравнение, равносильное предшествующему, т. е. уравнение, имеющее те же корни, и только их.
Перечислим стандартные уравнения, которые были нами изучены. Ответы учащихся.( линейное уравнение , квадратное уравнение, простейшее степенное уравнение х n =а). Преобразование уравнений к одному из стандартных является основным шагом в решении уравнения. Полностью алгоритмизировать процесс преобразования нельзя, однако полезно запомнить некоторые приемы, общие для всех типов уравнений.
1).Уравнение вида А(х)•В(х) = О, где А(х) и В(х) — многочлены относительно х, называют распадающимся уравнением .
Множество всех корней распадающегося уравнения есть объединение множеств всех корней двух уравнений А(х)=0 и В(х)=0. К уравнениям вида А(х)=0 применяется метод разложения на множители. Суть этого метода : нужно решить уравнение А(х)=0, где А(х)=А 1 (х)А 2 (х)А 3 (х). Уравнение А(х)=0 заменяют совокупностью простых уравнений: А 1 (х)=0,А 2 (х)=0,А 3 (х)=0. Находят корни уравнений этой совокупности и делают проверку. Метод разложения на множители используется в основном для рациональных и тригонометрических уравнений.
Решим уравнение (х 2 — 5х + 6) (х 2 + х — 2) = 0.
Уравнение распадается на два уравнения.
х 2 — 5х + 6 = 0 х 1 = 2 и х 2 = 3
х 2 + х — 2 = 0. х 3 = -2 и х 4 = 1
Значит, уравнение исходное имеет корни х 1 = 2, х 2 = 3, х 3 = -2, х 4 =1.
ПРИМЕР. Решим уравнение х 3 -7х+6=0.
х-1=0 , х 1 =1; х 2 +х-6=0, х 2 =2,х 3 =-3.
2).Уравнение вида , где А(х) и В(х) — многочлены относительно х.
Сначала решим уравнение
х 2 + 4х — 21 = 0. х 1 = 3 и х 2 = -7
Подставив эти числа в знаменатель левой части исходного уравнения, получим
х 1 2 — х 1 -6 = 9-3-6 = 0,
х 2 2 — х 2 — 6 = 49 + 7 — 6 = 50 ≠0.
Это показывает, что число х 1 = 3 не является корнем исходного уравнения, а число х 2 =- 7 — корень этого уравнения.
где А(х), В(х), С(х) и D(х) — многочлены относительно х, обычно решают по следующему правилу.
Решают уравнение А(х)•D(х) — С(х)·В(х) = 0 и отбирают из его корней те, которые не обращают в нуль знаменатель уравнения.
х 2 — 5х + 6 — (2х + 3) (х — 3) = 0.
х 1 = -5 и х 2 = 3.
Число х 1 не обращает в нуль знаменатель х — 3, а число х 2 обращает. Следовательно, уравнение имеет единственный корень = -5.
Найти корни рационального уравнения часто помогает замена неизвестного. Умение удачно ввести новую переменную- важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.
Решим уравнение х 8 + 4х 6 -10х 4 + 4х 2 + 1 = 0.
Число х 0 = 0 не является корнем уравнения, поэтому уравнение равносильно уравнению
х 4 + 4х 2 — 10 + + =0
Обозначим t = ,тогда х 4 + =t 2 -2 ,
получаем t 2 + 4t — 12 = 0, х 1 = 2 и х 2 = -6.
Следовательно, корни уравнения найдем, объединив все корни двух уравнений: =2, и =-6,
Первое уравнение имеет два корня -1 и 1, а второе уравнение не имеет действительных корней, поэтому уравнение имеет только два корня: -1 и 1. Ответ. -1; 1.
4). Симметрические уравнения.
Многочлен от нескольких переменных называют симметрическим многочленом, если его вид не изменяется при любой перестановке этих переменных.
Например, многочлены х + у, а 2 + b 2 — 1, zt и 5а 3 + 6ab + 5b 3 — симметрические многочлены от двух переменных, а многочлены х + у + г, а 3 + b 3 + с 3 , — симметрические многочлены от трех переменных.
В то же время многочлены х — у, а 2 –b 2 и а 3 + аb – b 3 — не симметрические многочлены.
Уравнение ax 4 +bx 3 +cx 2 +bx+a=0, где а R/ ,b R, с R называется симметрическим уравнением четвертой степени. Чтобы решить это уравнение необходимо:
1).Поделить обе части уравнения на х 2 и сгруппировать полученные выражения: .
2).Введение переменной уравнение приводится к квадратному.
Решите уравнение х 4 +5х 3 +4х 2 -5х+1=0.
Число 0 не является корнем уравнения. Поделим обе части уравнения на х 2 ≠0.
Системы рациональных уравнений.
Системы уравнений появляются при решении задач, в которых неизвестными являются несколько величин. Эти величины связаны определенной зависимостью, которые записываются в виде уравнений.
Уравнение, левая и правая части которого есть рациональные выражения относительно х и у, называют рациональным уравнением с двумя неизвестными х и у.
Если надо найти все пары чисел х и у, каждая из которых является решением каждого из данных уравнений с двумя неизвестными х и у, то говорят, что надо решить систему уравнений с двумя неизвестными х и у и каждую такую пару называют решением этой системы.
Неизвестные могут обозначаться и другими буквами. Аналогично определяется система уравнений, число неизвестных в которой больше двух.
Если каждое решение первой системы уравнений является решением второй системы, а каждое решение второй системы уравнений является решением первой системы, то такие системы называют равносильными. В частности, равносильными считаются две системы, не имеющие решений.
Например, равносильны системы
1). Способ подстановки .
ПРИМЕР 1. Решим систему уравнений
Выразив у через х из первого уравнения системы, получим уравнение:
Решив уравнение 5x 2 -4(3x-1)+3(3x-1) 2 =9, найдем его корни х 1 = 1 и х 2 = . Подставив найденные числа х 1 и х 2 в уравнение у = 3х — 1 , получим у 1 = 2
и у = Следовательно, система имеет два решения: (1; 2) и ( ; )
2). Метод алгебраического сложения.
ПРИМЕР 2. Решим систему уравнений
Оставив без изменения первое уравнение системы и сложив первое уравнение со вторым, получим систему равносильную системе.
Все решения системы есть объединение всех решений двух систем:
Решив каждую из этих систем, найдем все решения системы :
3). Метод введение новых неизвестных.
ПРИМЕР 3. Решим систему уравнений
Обозначив u = ху, v = х — у, перепишем систему в виде
Найдем ее решения: u 1 = 1, v 1 = 0 и u 2 = 5, v 2 = 4. Следовательно, все решения системы есть объединение всех решений двух систем:
Решив методом подстановки каждую из этих систем, найдем ее решения системы: (1; 1), (-1; -1), (5; 1), (-1; -5).
Ответ. (1; 1), (-1; -1), (5; 1), (-1; -5).
4). Уравнение вида ах 2 + bху + су 2 = 0, где а, b, с — данные неравные нулю числа, называют однородным уравнением относительно неизвестных х и у.
Рассмотрим систему уравнений, в котором есть однородное уравнение.
ПРИМЕР 4. Решим систему уравнений
Обозначив t = , перепишем первое уравнение системы в виде t 2 +4t+3=0.
Уравнение имеет два корня t 1 = -1 и t 2 = -3, поэтому все решения системы есть объединение всех решений двух систем:
Решив каждую из этих систем, найдем все решения системы:
При решении некоторых систем помогает знание свойств симметрических многочленов.
Введем новые неизвестные α = х + у и β= ху, тогда, х 4 +у 4 = α 4 -4 α 2 β+2 β 2
Поэтому систему можно переписать в виде
Решим квадратное уравнение относительно β: β 1 =6, β 2 =44.
Следовательно, все решения системы являются объединением
всех решении двух систем:
Первая система имеет два решения х 1 = 2, у 1 = 3 и х 2 = 3, у 2 =2, а вторая система не имеет действительных решений. Следовательно, система имеет два решения: (х: 1 ; у 1 ) и (х 2 ;у 2 )
Сегодня мы подвели итоги изучения темы рациональные уравнения. Мы поговорили об общих идеях, общих методах, на которых основана вся школьная линия уравнений.
Выделили методы решения уравнений:
1) метод разложения на множители;
2) метод введения новых переменных.
Расширили представления о методах решения систем уравнений.
На следующих 4 уроках проведем практические занятия. Для этого необходимо выучить теоретический материал, и подобрать из учебника по 2 примера на рассмотренные методы решения уравнений и систем уравнений, на 6 уроке будет проведен семинар по этой теме, для этого необходимо подготовить вопросы: формула бинома Ньютона, решение симметрических уравнений 3,5 степени. Заключительный урок по этой теме — зачет.
- Алгебра и начала анализа: учеб. Для 10кл. общеобразоват. учреждений/[С.М.Никольский, М.К. Потапов.].-5-е изд., доп.-М.: Просвещение , 2006.-432с. Стр.65-74., 45-47.
- Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов/сост. Г.И.Ковалева, Т.И. Бузулина — Волгоград: Учитель,2009.-494с. – стр. 62-72,194-199.
- Титаренко А.М. Математика : т9-11 классы: 6000 задач и примеров/А.М. Титаренко.-М.:Эксмо,2007.-336с.
Много можно говорить об уравнениях. В этой области математики существуют вопросы, на которые математики еще не дали ответа. Возможно, кто-то из вас найдет ответы на эти вопросы.
Альберт Эйнштейн говорил: « Мне приходиться делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента. А уравнения будут существовать вечно ».
Уроки 2-5 отводиться практическим занятиям. Основным видом занятий на этих уроках является самостоятельная работа учащихся по закреплению и углублению теоретического материала, изложенного на лекции. На каждом из них проводится повторение вопросов теории и опрос учащихся. На основе самостоятельной работы на уроке и дома обеспечивается повторение и усвоение вопросов теории, ведется целенаправленная работа по выработке умений и навыков решения задач различного уровня сложности, проводится опрос учащихся. Цель: закрепить и углубить теоретический материал изложенный на лекции, научиться применять его на практике, усвоить алгоритмы решения типовых примеров и задач, добиться, чтобы все учащиеся усвоили основное содержание изучаемого раздела на уровне программных требований.
На семинар отводится 6-й и 7-й уроки, причем целесообразно на 6-м уроке провести семинар, а 7-м- зачет.
План урока – семинара.
Цель: повторение, углубление и обобщение пройденного материала, отработать основные методы, способы и приемы решения математических задач, приобретение новых знаний, обучение самостоятельному применению знаний в нестандартных ситуациях.
1. В начале урока организуется программный контроль. Цель проведения работы- проверка сформированности умений и навыков выполнения несложных упражнений. В процессе фронтального опроса учеников, неверно указавших номер ответа, учитель выясняет, какие из заданий вызвали затруднение. Далее ведется устная или письменная работа по устранению ошибок. На проведение программированного контроля отводится не более 10 минут.
2. Дифференцированный опрос нескольких учащихся по вопросам теории.
3. Историческая справка о возникновении и развитии понятия уравнения (сообщение ученика). Формула бином Ньютона. Решение симметрических уравнений третьей степени, четвертой степени, пятой степени.
х 4 -2х 3 -х 2 -2х+1=0
2х 4 +х 3 -11х 2 +х+2=0
х 5 -х 4 -3х 3 -3х 2 -х+1=0
2х 5 +3х 4 -5х 3 -5х 2 +3х+2=0
4. Решение примеров, проверка готовности учащихся к выполнению контрольной работы – это одна из главных задач семинара.
Проведение зачета не означает отказ от текущего контроля знаний учащихся. Оценки выставляются на практических и семинарских занятиях. На зачет выносятся некоторые типичные упражнения. Заранее ученикам сообщается, какой теоретический материал и упражнения будут представлены на зачете. Приведем содержание одной из карточек для проведения зачета по рассматриваемой теме.
Решите уравнения: (х+3) 4 +(х 2 +х-6) 2 =2(х-2) 4
🎥 Видео
9 класс, 1 урок, Рациональные неравенстваСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 60 часть. 9 класс.Скачать

ЗАДАНИЕ 8 ЕГЭ (ПРОФИЛЬ). РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВАСкачать

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Классический способ решения рациональных неравенств #ShortsСкачать

Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Рациональные неравенства. 8 класс.Скачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 64 часть. 9 класс.Скачать

Как решать неравенства? 9 - 11 класс. Вебинар | Математика TutorOnlineСкачать

Равносильные уравнения. Рациональные уравнения - 8 класс алгебраСкачать