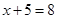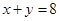Конспект урока линейное уравнение с двумя переменными 7 класс мерзляк

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Конспект урока по алгебре 7 класс «Линейное уравнение с двумя переменными»
методическая разработка по алгебре (7 класс) по теме

«Линейное уравнение с двумя переменными»

Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Скачать:

Видео:Видеоурок ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Предварительный просмотр:

МБОУ Правдовская школа

Святогор Наталья Николаевна.

Конспект урока по алгебре в 7-м классе по теме:

«Линейное уравнение с двумя переменными»

Образовательные — Дать определение линейного уравнения с двумя переменными. Выяснить, что значит решить линейное уравнение с двумя переменными.

Развивающие — развивать навыки мыслительной деятельности учащихся способствовать развитию познавательной активности, логическому мышлению Воспитательные — воспитание интереса к предмету

Тип урока : изучение нового материала

Планируемые результаты : знают определение линейного уравнения с двумя переменными, умеют выражать одну переменную через другую, находить пары решений

Оборудование : учебник, мультимедийная доска, карточки с заданиями.

Приветствие. Проверка готовности к уроку.

Ручки, книги и тетрадки

На парте лежат в порядке.

Прозвенел уже звонок Начинаем наш урок.

2.Сообщение темы и цели урока.

Предлагаю учащимся назвать тему и определить цель урока.

Слайд 1 На доске записаны два уравнения : 2х = 5, Зх +5у = 7

-Как называются выражения записанные на доске? (предполагаемый ответ: уравнения).

-Какое из двух уравнений вы изучали? Как оно называется? (предполагаемый ответ: линейное уравнение с одной переменной). Чем отличается второе уравнение от первого.

Слайд 2 Попробуйте назвать тему урока ( предполагаемый ответ: линейное уравнение с двумя переменными).

Слайд 3 Попробуйте назвать цель урока.

3.Актуализация опорных знаний.

Для изучения новой темы нам необходимо повторить понятия пройденного

Письменное задание : Продолжите фразу :

1. Линейным уравнением с одной переменной называется .
2. Решить уравнение это значит найти .
3. Корнем уравнения называется.

Слайд 6 . Проверка выполненного задания

1. Изучение нового материала.

Слайд7. Задание на доске:

Из данных выражений выбрать и записать в столбик линейные уравнения с одной переменной 2х=4, Зх-4=5х, 4х-2=у, 2х=3у, Зв-24, Зх-12=4, х 2 -у=5, х+у=1, ху+2=1, 2а+7

Предлагаю ответить на вопрос: Как называются выражения записанные во 2 и 3 столбиках?

Предлагаю учащимся дать определение уравнения с двумя переменными и

линейного уравнения с двумя переменными.

Слайд 8 . Даю определение уравнения с двумя переменными и линейного уравнения с двумя переменными.

Задание 1: Придумайте линейное уравнение с двумя переменными.

Задание 2. Проверь себя

Из данных уравнений назовите линейные уравнения с двумя переменными.

1)7-х=у; 2)5х-у=4; 3)2ху+5=х;4)2х-0,4у+7=6; 5)х=ху+8; 6)у- 4х+2у=7 Слайд 10 Дать определение решения уравнения

Слайд 11. Метод подбора. Предлагаю учащимся для уравнения 2х+у=5 подобрать пару чисел, которая является решением уравнения. Предлагаю свое решение. Обращаю внимание на количество решений.

Слайд 12 . Показываю как выразить одну переменную через другую.

Слайд 13 . Индивидуальная работа .Задание на карточке:

Видео:7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Урок по теме «Линейное уравнение с двумя переменными», алгебра, 7 класс

Первый урок в теме «Системы линейных уравнений».

Просмотр содержимого документа
«Урок по теме «Линейное уравнение с двумя переменными», алгебра, 7 класс»

Дата проведения __________

Тема урока. Линейное уравнение с двумя переменными

Цель урока: сформировать представление об уравнении с двумя переменными и его решения; осознать содержание понятия «график уравнения с двумя переменными»; выработать умения: отбирать проверкой решение уравнения с двумя переменными; работать с готовым графиком уравнения с двумя переменными; преобразовывать уравнения вида у=f(x) и вычислять решение уравнения с двумя переменными.

Тип урока: усвоение новых знаний.

І. Организационный момент

ІІ. Актуализация опорных знаний

Выполнение устных упражнений:

Что значит «решить уравнение»?

3. Составить уравнения по условию задачи:

1) длина прямоугольника х, ширина 3 м, а периметр 20 м;

2) ширина прямоугольника х, длина на 4 м больше, а периметр 20 м;

3) ширина прямоугольника х, длина у м, а периметр 20 м.

Если можно, решите уравнения, найдите длины сторон прямоугольника.

4. Принадлежит ли графику функции у=3х+2 точки А (1;-5), В(3;11), С(0;2)? Почему?

ІII. Формулирование цели и задач урока

После повторения основных понятий, изученных в теме «Линейные уравнения с одной переменной», и выполнения устных упражнений, составления уравнений вместе с учащимися формулируем цели: познакомиться с тем новым видом уравнения, что встретился нам во время решения одной из задач.

IV. Изучение нового материала

Новое понятие уравнения с двумя переменными вводится на примерах (так же, как и уравнения с одной переменной), а затем формулируется определение уравнения с двумя переменными и определение решения такого уравнения, как упорядоченной пары чисел — значений переменных, обращающие уравнение в верное равенство, так же, как и корень уравнения с одной переменной. Понятие равносильных уравнений с двумя переменными строится на известных учащимся понятий равносильных уравнений и свойств равносильных уравнений.

Записи в тетрадях учащихся могут иметь вид сравнительной таблицы, в которой выделены ключевые слова.

Уравнение с одной переменной

Уравнение с двумя переменными

Равенство, содержащее неизвестное число, обозначенное буквой (переменная)

Равенство, содержащее два неизвестных числа, обозначенных буквой (переменные)

Корень уравнения с первой переменной-значение переменной, превращающей уравнение в правильное равенство

Решение уравнения с двумя переменными — упорядоченная пара чисел (х;у), при которых уравнение превращается на верное равенство

уравнения с одной переменной — имеют одинаковые корни или вообще не имеют корней

уравнения с двумя переменными — имеют одни и те же решения или оба не имеют решений

Свойства равносильных уравнений

Фигура, которая состоит из точек (х;у), таких, что их координаты — решения уравнения

V. Закрепление материала. Выработка умений

І. Выполнение устных упражнений:

1. Является ли решением уравнения х−2у=6 пара чисел (0; 0); (2; –2); (0; 3); (6; 0)?

2. Точки А(…;0), В(0;…), С(1;…), D(…;−3) принадлежат графику уравнения 3х–у=6. Найти пропущенные координаты.

3. Выразить переменную у через переменную х (представить уравнение в виде у=f(x)) путем выполнения тождественных преобразований: х+у=3; 3х+3у=0 ; х−у=4.

Используя полученную формулу, найдите два каких-либо решения каждого уравнения.

ІІ. Выполнение письменных упражнений:

1. Пары значений х и у внесены в таблицу. Какие из них являются решениями уравнений: 1) х 2 +у 2 =25; 2) х 2 −у 2 =7?

Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Конспект урока по алгебре «Линейное уравнение с двумя переменными» для 7 класса

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Линейное уравнение с двумя переменными.

УМК: Алгебра 7 класс: учеб. для общеобразовательных организаций / А.Г. Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2013.

Тема: Линейное уравнение с двумя переменными.

Тип урока : урок формирования умений и навыков.

o знакомство учащихся с понятиями линейного уравнения с двумя переменными и его решения;

o выработка умения выражать одну переменную линейного уравнения с двумя переменными через другую;

o развитие познавательных навыков обучающихся, критического и творческого мышления;

o воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе.

Личностные : ф ормирование навыков организации анализа своей деятельности объективной самооценки и взаимооценки.

Предметные: формирование знаний о линейном уравнении с двумя переменными, его решении и свойствах.

Познавательные: осуществление поиска нужной информации в учебном пособии; понимание знаков, символов, умение их применять; понимание заданного вопроса, в соответствии с ним построение устного ответа; выдвижение и обоснование гипотез, предложение способов их проверки.

Регулятивные: сопоставление способов и результата своих действий с заданным эталоном.

Коммуникативные: умение устанавливать рабочие отношения; эффективно сотрудничать.

Оборудование: компьютер, мультимедийный проектор, экран.

I Организационный момент (Приветствие. Проверка готовности учащихся к уроку). Мотивация

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. Урок длится всего 45 мин, и мне бы очень хотелось, чтобы они были потрачены с пользой.

II. Проверка домашнего задания

Какую тему мы с вами изучили на предыдущих уроках? (Уравнения с двумя переменными.)

Давайте проверим ваше домашнее задание.

III. Повторение пройденного материала. Актуализация опорных знаний учащихся.

На доске записано:5х; 5х + 7, 5х + 7 = 12.

— Дайте определение записанным выражениям.

— Что называется уравнением?

— Сформулируйте определение линейного уравнения с одной переменной.

— Что значит решить уравнение?

— Что называется корнем уравнения?

— Приведите свой пример линейного уравнения с одной переменной.

— Чем отличаются уравнения 5х+7=12 и 5х+7у=12?

— Как называется первое уравнение?

— Попытайтесь сформулировать определение второго уравнения.

— Как ы думаете, какова тема нашего сегодняшнего урока? Запишем тему урока в тетради.

— Давайте попробуем провести параллель между известным нам материалом и новым.

I V. Изучение нового материала.

— Давайте вспомним всё, что мы знаем о линейных уравнениях.

— Какой тип уравнения нам известен? (линейное уравнение с одной переменной)

— Вспомним определение линейного уравнения с одной переменной.

— Что называется корнем линейного уравнения с одной переменной?

— Сформулируем все свойства линейного уравнения с одной переменной.

— Заполним первую строку таблицы.

Что является решением уравнения

Линейное уравнение с одной переменной.

ах=в, где х – переменная, а,в- числа.

Значение х, при котором уравнение обращается в верное равенство

1) перенос слагаемых из одной части уравнения в другую, изменив их знак на противоположный.

2) умножение и деление обеих частей уравнения на одно и тоже, не равное нулю число.

Линейное уравнение с двумя переменной.

где х,у – переменные, а,в.с – некоторые числа.

Значения х, у, при которых уравнение обращается в верное числовое равенство.

3) равносильность уравнений.

— Приведите пример уравнения с двумя переменными. (Записать в тетради)

— Что бы вам хотелось узнать о линейном уравнении с двумя переменными?

— Попробуйте сформулировать цель урока. (Совместно с учениками поставить задачи и вопросы к уроку)

Возможные ответы учащихся: знать определение линейно гоуравнения с двумя переменными; научиться находить линейные уравнения 2 степени среди других уравнений; выяснить как решаются эти уравнения.

— Давайте вместе искать ответы на поставленные вами вопросы.

Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где a,b и c – некоторые числа, а x и y –переменные.

— Среди данных уравнений найдите линейные уравнения с 2 переменными и назовите коэффициенты а, в, с: а) 6х = 96; б) 7х-5у = 2; в) 4х + 3у⁷; г) х + у = 15; д) х-у = 3.

— Линейные уравнения с двумя переменными, как и все уравнения надо решать.

— Найдите корни уравнения х-у = 12

— Сколько решений имеет это уравнение? (Множество)

— Как вы нашли корни уравнения? (Подбором)

— Как выяснить будет ли данная пара чисел корнем уравнения? (Проверить подстановкой)

— Уравнение x – y = 12 при x = 8, y =-4 обращается в верное равенство 8 – (-4) = 12. Говорят, что пара значений переменных x = 8, y = -4 является решением этого уравнения). Попробуйте дать определение решения линейного уравнения с двумя переменными? (Дети дают определение)

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

Пары значений переменных иногда записывают короче: (х; у) В такой записи на первом месте пишут значение x а на втором — y. Одно из решений рассмотренного уравнения может быть записано в виде (8; -4).

Уравнения с двумя переменными, имеющие одни и те же решения (или не имеющие решений), называются равносильными.

— Приведите примеры равносильных уравнений. (х+у=7 и х=7-у; =-4 и = -2)

Уравнения с двумя переменными обладают такими же свойствами, что и уравнения с одной переменной:

1. Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или разделить на одно и то же число (не равное нулю), то получится уравнение равносильное данному.

— По аналогии с первой строкой, давайте заполним вторую строку таблицы, тем самым обобщая новый материал.

Рассмотрим уравнение 4x + 2y = 10. Используя свойства уравнений, выразим одну переменную через другую.

Можем выразить переменную х через переменную у. Для этого оставим 4х в левой части уравнения, а 2у перенесем в правую, изменив его знак. Получаем равносильное уравнение 4х = – 2у+10.

Разделим каждую часть этого уравнения на число 4, получим равносильное уравнение

Для того, чтобы выразить переменную у через переменную х, сначала перенесем 4 x из левой части в правую, изменив его знак. Получаем равносильное уравнение 2 y = 1 0 — 4 x.

Разделим каждую часть этого уравнения на число 2, получим равносильное уравнение

Таким образом, мы выразили одну переменную через другую.

Пользуясь этим равенством, для каждого значения x можно вычислить значение y.

Если x = 2, то y = 5 — 2· 2 = 1.

Если x = -2, то y = 5 — 2· (-2) = 9. Пары чисел (2; 1), (-2; 9) – решения данного уравнения. Таким образом, данное уравнение имеет бесконечно много решений.

V. Работа с учебником. Открываем учебники на странице 195.

— Найдите в учебниках место, где выделена главная идея темы нашего урока.

а) Устно выполняем № 28.1, №28.2, №28.4.

б) Письменно решаем № 28.3. Делают в тетрадях самостоятельно, затем на доске.

в) № 28.8(1;4) № 28.10(1;2) Работа в парах. Разбор у доски.

VI. Историческая справка.

Рене Декарт (1596-1650) ­– французский философ, математик и физик.

Создал основы аналитической геометрии, ввел понятие переменной величины, разработал метод координат. Осуществил связь алгебры с геометрией.

Пьер Ферма (1601-1665) ­– французский математик, один из создателей аналитической геометрии и теории чисел. Занимался теорией решения алгебраических уравнений с несколькими переменными.

V I . Самостоятельная работа с самопроверкой с помощью экрана в классе.

1. Выпишите линейное уравнение с двумя переменными:

а) 3 + 6у = 5; б) ху = 16; в) 2х – у = 5.

2. Является ли решением уравнения2х — у = 5 данная пара чисел?

3. Выразите из линейного уравнения 3х – 4у = 12

а) х через у б) у через х.

4. Найдите три, каких-либо решения уравнения х + у = 17.

V II . Итог урока. Обобщение пройденного материала на уроке. Выставление оценок.

Давайте попробуем дать ответы на вопросы, поставленные в начале урока.

— Какие уравнения называются линейными с двумя переменными?

— Что значит решить линейное уравнение с двумя переменными?

— Что называется решением уравнения с двумя переменными?

— Можем ли мы найти все решения уравнения? (Нет, так как их бесконечное количество)

— Как записывается корень уравнения?

— Какие уравнения называются равносильными?

— Перечислите свойства линейного уравнения с двумя переменными

V III .Рефлексия. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

сегодня я узнал…

я выполнял задания…

я почувствовал, что…

у меня получилось …

IX . Домашнее задание: п.28, № 28.5, №28.11, № 28.51-повтор.

📹 Видео

Линейное уравнение с 2 переменными, 7 классСкачать

Линейное уравнение с двумя переменными и его график | Алгебра 7 класс #43 | ИнфоурокСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

МЕРЗЛЯК-7 АЛГЕБРА УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИСкачать

МЕРЗЛЯК-7. ЛИНЕЙНЫЕ УРАВНЕНИЯ. ПАРАГРАФ-2Скачать

Линейное уравнение с двумя переменными 7 классСкачать

Алгебра 7 Линейное уравнение с двумя переменными и его графикСкачать

Линейное уравнение с двумя переменными. 6 класс.Скачать

МЕРЗЛЯК-7 АЛГЕБРА ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК. ПАРАГРАФ-25Скачать

Линейное уравнение с двумя переменнымиСкачать

Линейное уравнение с двумя переменными.Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать