Метод конечных элементов (МКЭ, по-английски FEM — Finite Element Method) состоит в том, что все тело разбивают на некоторое количество частей (элементов) конечного (а не бесконечно малого) объема, настолько простых по форме и внутреннему устройству, что интегрирование уравнений внутри каждого из них не вызывает затруднений. Для приближенного решения задачи в целом необходимо обеспечить только стыковку элементов между собой. Условия стыковки записывают в виде алгебраических уравнений. В некоторых случаях эти уравнения независимы друг от друга и могут быть решены по одиночке, но чаще они образуют систему уравнений, порядок которой зависит от числа конечных элементов.
Таким образом, МКЭ состоит в замене дифференциального или интегрального уравнения на систему алгебраических уравнений. Существует ряд методов, родственных МКЭ: метод конечных разностей, метод граничных элементов и др. Каждый из них в чем-то превосходит МКЭ при решении определенного ограниченного круга задач. МКЭ является наиболее гибким и универсальным.
Для упрощения процедуры элемент обычно выбирают простой формы (треугольной или четырехугольной — для плоских задач, призматической или пирамидальной — для пространственных; рис. 2.2) и описывают распределение потенциала внутри него простой функцией (обычно полиномом невысокого порядка). Поэтому при небольшом числе элементов решение может получиться весьма грубым. Однако доказано математически, что при измельчении элементов погрешность уменьшается и решение неограниченно приближается к точному. Чем грубее и проще элементы, тем мельче они должны быть для достижения заданной точности.
Таким образом, наличие погрешности при использовании конечного элемента не является свидетельством его непригодности, если эта погрешность убывает при уменьшении размеров элемента и в пределе стремится к нулю. Это не значит, что все виды элементов равноценны. При прочих равных условиях следует предпочитать элементы, дающие наименьшую погрешность при данных размерах и более быстрое ее убывание при уменьшении размеров. Рис. 2.2. Виды конечных элементов
Поскольку число элементов и порядок системы уравнений для сложных сварочных задач достигает десятков тысяч, решение такой большой системы уравнений является наиболее серьезным этапом процедуры МКЭ. Часто идут на усложнение элементов (повышение степени полинома внутри элемента) для того, чтобы уменьшить число элементов и порядок системы уравнений. В конкретных случаях большую экономию может дать использование для интерполяции внутри элемента взамен полинома других функций, близких к ожидаемому решению задачи, но это снижает универсальность программного обеспечения.
На снижение порядка системы уравнений направлена и суперэлемент — ная процедура. Несколько обычных элементов объединяют в суперэлемент, исключая из системы уравнений неизвестные, связанные с внутренними границами между объединяемыми элементами, и оставляя те, которые участвуют в стыковке суперэлемента с другими суперэлементами. Тогда число уравнений в системе для суперэлементной модели уменьшается. После решения этой системы необходимо вернуться к внутреннему устройству суперэлемента и найти значения исключенных ранее внутренних неизвестных.
По сути дела, общее число операций не уменьшается, но задача упрощается за счет ее разделения на несколько этапов. Сокращение расчетов может быть получено, если в модели много одинаковых суперэлементов. Тогда часть операций для них можно не повторять.
Процедура МКЭ в принципе достаточно проста. Функционирующая программа может быть написана и отлажена за неделю. Однако область применения такой программы весьма ограничена. Программа среднего уровня, содержащая средства подготовки данных (среду, аналогичную AutoCAD), эффективные процедуры составления и решения уравнений и визуальную систему анализа результатов моделирования, требует существенно больших затрат.
В мире существуют десятки коммерческих программных комплексов МКЭ (наиболее известны NASTRAN, ANSYS), в том числе специализированных для решения сварочных и других технологических задач (SYSWELD, MARC). На их создание были затрачены большие усилия, и тем не менее нельзя назвать ни одного, пригодного для решения всех возникающих задач. Поскольку внутренняя часть программного комплекса является «черным ящиком», то довольно трудно бывает самостоятельно приспособить его к решению задачи, не предусмотренной разработчиками. Еще одно обстоятельство оказывается не в пользу коммерческих комплексов — огромные размеры текста программ (сотни мегабайтов) и обязанность поддерживать совместимость новых версий с предыдущими. Теряется гибкость и с трудом осваивается решение принципиально новых задач, а изменения в аппаратном обеспечении (например,
Рис. 2.3. Схема конечного элемента с двумя узлами 1 и 2
переход с больших ЭВМ на персональные компьютеры) имеют для таких комплексов катастрофические последствия.
Видео:Метод конечных элементов. Основы 1.1.4 - Слабая форма дифференциального уравненияСкачать

Вследствие этого создание новых комплексов МКЭ, прежде всего не универсальных, а направленных на решение конкретного круга задач, сохраняет свою актуальность. В этой главе описаны элементы трех таких комплексов, разработанных в Москве. Их развитие продолжается и в настоящее время.
Даже если специалист не ставит перед собой задачу’ разработки новых программ, а пользуется готовым комплексом МКЭ, ему полезно понимать внутреннее устройство и механизм работы комплекса для более эффективного его применения. Под руководством разработчиков вполне осуществимо добавление к работающему комплексу недостающих элементов. Некоторые коммерческие комплексы предусматривают для этого встроенный язык программирования и инструкции по его применению.
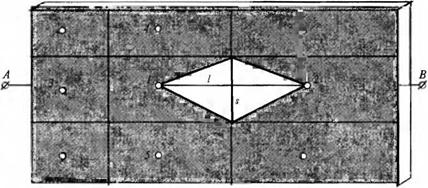
Рассмотрим простейшую конечно-элементную модель (КЭМ) для плоской пластины. Пусть имеется пластина, через которую течет ток, и на ней обозначены точки, в которых требуется рассчитать потенциал. Разобьем пластину на ячейки (клетки) так, чтобы границы проходили на равном расстоянии от соседних точек (узлов) (рис. 2.3).
Конечный элемент (КЭ) позволяет установить, какой ток потечет из клетки 2 в клетку 1 через их границу s, если известна разность потенциалов между этими точками. Распределение потенциала по длине элемента аппроксимируем полиномом первой степени, напряженность поля во всех
точках элемента одинакова и равна Е-^г^х. Плотность тока, согласно £
закону Ома (2.1), j = —, поскольку материал изотропный и сопротивление Р
во всех направлениях одинаково. Ток через элемент равен
Рис. 2.4. Принципиальная схема конечно-элементной модели пластины
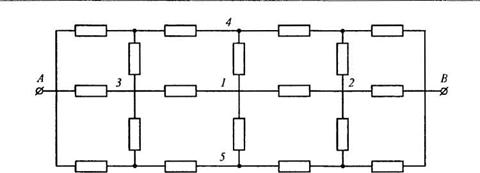
Таким образом, КЭ эквивалентен сопротивлению R, включенному между узлами 7 и 2. Оно равно сопротивлению проводника из такого же материала, длиной / и сечением s (см. рис. 2.3). Если добавить КЭ для каждой пары соседних узлов, то они покроют всю пластину. Если считать, что все заряды, попавшие в одну из клеток, находятся в узле, то всю пластину можно изобразить в виде принципиальной электрической схемы (рис. 2.4). Согласно классификации КЭ, рассмотренный элемент следует называть стержневым линейным двухузловым.
Если известны потенциалы на краях пластины и сопротивления элементов, то можно найти токи и потенциалы внутренних точек по законам Кирхгофа, которые приводят к системе линейных уравнений, т. е. к типичной процедуре МКЭ. Естественно, ввод данных, составление и решение системы уравнений и представление результатов должны быть реализованы в компьютерной программе.
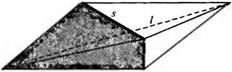
Моделирование объемных тел. Моделирование объемных тел сложной формы как правило, существенно сложнее, чем плоских, и требует применения более сложных элементов. Однако рассмотренный простейший двухузловой элемент без существенных изменений может быть превращен из плоского в объемный. На рис. 2.5 видно, что если плоский элемент состоит из двух призм, высота которых равна толщине моделируемого плоского тела, то объемный — из двух пирамид. Как призмы, так и пирамиды примыкают с двух сторон к поверхности s, разделяющей соседние ячейки, а ребра призм и пирамид соединяют точки контура поверхности s с узлами 7 и 2. Отрезок 7—2 длиной / перпендикулярен плоскости s, и точка пересечения с этой плоскостью делит его пополам.
Рис. 2.5. Плоский и объемный элементы
Если трехмерное тело разбить на ячейки в виде прямоугольных параллелепипедов, то, соединив каждую грань, разделяющую две соседние ячейки с узлами, расположенными в центрах ячеек, получим такой элемент. Очевидно, что в совокупности элементы заполнят весь объем тела.
Видео:Основы метода конечных элементов. Часть 2. Функции формы конечного элементаСкачать

Модель протекания тока и распределения потенциалов в теле можно представить в виде принципиальной схемы, аналогичной рис. 2.4, где каждый элемент изображен в виде сопротивления, присоединенного между двумя узлами.
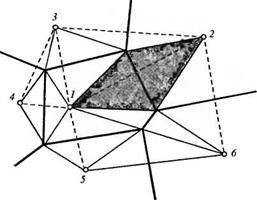
Ячейки, на которые разбита модель, имеют прямоугольную форму, если заданные точки (узлы) 1, 2, 3. расположены ровными рядами, как на рис. 2.3. При произвольном расположении узлов на плоскости или в пространстве построение ячеек, границы которых равноудалены от ближайших узлов, также возможно, хотя ячейки будут иметь более сложную форму (рис. 2.6).
Возможность применения нерегулярной сетки, обеспечивающей заполнение элементами произвольной области со сложным очертанием границы, а также сгущение сетки в отдельных местах, требующих повышения точности расчета, является основным преимуществом МКЭ по сравнению с более простым методом сеток.
Рис. 2.6. Разбиение на элементы с нерегулярной сеткой
Г раничные условия.
Чтобы рассчитать токи и потенциалы по модели, изображенной в виде принципиальной схемы на рис. 2.4, необходимы граничные условия, т. е. параметры недостающей части электрической цепи, присоединенной к модели в узлах А и В (см. рис. 2.3 и 2.4).
При моделировании внешние границы элементов ничем не отличаются от внутренних: через каждую из них
проходит электрический ток согласно закону Ома. Однако в зависимости от устройства внешнего участка цепи различают три рода граничных условий.
Условие первого рода: задан электрический потенциал на границе. Это соответствует наличию во внешней цепи стабилизированного источника питания, поддерживающего постоянное напряжение, не зависящее от сопротивления модели. В этом случае потенциал во всех точках соответствующей границы заранее известен, а плотность тока через нее зависит от разности этого потенциала и потенциала ближайшего внутреннего узла согласно закону Ома (2.1).
Условие второго рода: задан ток или плотность тока на границе. Это соответствует наличию во внешней цепи другого источника питания, поддерживающего постоянный ток, не зависящий от сопротивления модели. В этом случае граница является узлом, потенциал в котором зависит от потенциала ближайшего внутреннего узла и определяется в ходе решения задачи. Частным случаем такого граничного условия является нулевая плотность тока (адиабатическая граница). Для задач электропроводности это соответствует границе проводника с изолятором. На рис. 2.3 такие условия действуют на всех внешних границах модели, кроме граничных узлов АиВ.
Условие третьего рода представляет собой наиболее общий случай, когда ток или плотность тока на границе связаны с ее потенциалом некоторым уравнением. Это соответствует, например, обычному источнику питания с внутренним сопротивлением. Создаваемое им напряжение снижается по мере увеличения тока. Очевидно, что первые два рода граничных условий являются крайними частными случаями третьего.
Нелинейные задачи. Рассмотренные уравнения протекания тока являются линейными (зависимость тока от напряжения в законе Ома выражается уравнением прямой линии). В этом случае уравнения Кирхгофа, из решения которых можно найти потенциалы узлов, образуют систему линейных уравнений. Нелинейность уравнений может возникнуть в двух случаях:
• если уравнения моделируемых физических явлений отличаются от линейных;
• если входящие в уравнения коэффициенты не являются константами, а зависят от результатов решения (например, если удельное сопротивление проводника зависит от плотности тока).
Видео:Метод конечных элементов. Основы 1.1.1 - ВведениеСкачать

Внимание к нелинейности вызвано тем, что методы решения системы нелинейных уравнений гораздо сложнее и требуют большего объема вычислений, чем линейных. Как правило, нелинейную систему решают итерационно (методом последовательных приближений) на основе линеаризации: кривые нелинейных уравнений заменяют прямыми, касательными к ним, или секущими и постепенно уточняют коэффициенты, входящие в уравнения этих прямых.
Стационарные и нестационарные задачи. Поскольку скорость движения зарядов в проводнике велика, то переходные процессы при изменении граничных условий протекают очень быстро и во многих случаях их можно игнорировать, рассматривая только установившееся равновесное распределение потенциалов и токов. В этом случае результат решения зависит не от начального распределения зарядов и потенциалов, а от граничных условий. Такие задачи называют стационарными или эллиптическими, поскольку в их основе лежит дифференциальное уравнение Лапласа эллиптического типа.
Уравнения теплопроводности и диффузии практически совпадают с уравнениями электропроводности (вместо закона Ома в них используются аналогичные законы Фурье и Фика). Однако скорость протекания этих процессов значительно ниже. Вследствие этого не всегда можно ограничиться расчетом установившегося поля температур или распределения примесей, во многих случаях требуется определять распределение параметров во время переходного процесса. В этом случае решение зависит не только от граничных условий, но и от начального состояния и времени. Соответствующее уравнение отличается от уравнения Лапласа добавлением производной по времени и называется уравнением параболического типа:
* дх > 8у2 г 8z 8t К
Очевидно, что эллиптическое уравнение (2.2) является частным случаем уравнения (2.3). После завершения переходного процесса скорость изменения потенциала стремится к нулю и уравнение приобретает эллиптический вид.
Рассмотрим, как изменяется физическая картина при переходе от стационарной задачи электропроводности к нестационарной задаче теплопроводности. Аналогом потенциала является температура, аналогом плотности заряда — теплосодержание, аналогом тока — поток теплоты. Если в электрической задаче благодаря быстрому перемещению зарядов не происходит их накапливание в точках тела и потенциалы этих точек сразу принимают равновесные значения, то перемещение теплоты происходит недостаточно быстро, теплота накапливается в одних точках и убывает из других, теплосодержание и температура в этих точках изменяются. Эти изменения приводят к перераспределению тепловых потоков, и, лишь когда переходный процесс завершается, наступает равновесное установившееся состояние.
Из сопоставления этих двух задач ясно, что для решения нестационарной задачи нужно к первым двум этапам (необходимым и для стационарной задачи) добавить еще два. Таким образом, имеем следующие этапы:
1) уравнение потоков массы или энергии (закон Ома, Фурье, Фика и т. д.);
2) граничные условия 1, 2 и 3-го рода;
3) начальные условия — исходное распределение температур или примесей;
4) условия накопления массы или энергии.
Применительно к тепловой задаче п. 4 соответствует уравнение теплоемкости, связывающее теплосодержание с температурой.
Явная и неявная схемы решения. Особенностью нестационарной задачи является необходимость последовательного прослеживания промежуточных предыдущих состояний тела для правильного расчета текущего состояния, т. е. истории процесса, в то время как для стационарного процесса истории не существует, каждое состояние может быть рассчитано независимо от предыдущих.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

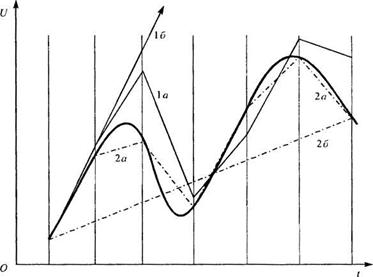
Если историю процесса прослеживать с достаточно мелким шагом во времени, то можно пренебречь влиянием на температуру данной точки тела температуры других точек, удаленных от нее, т. е. считать, что на каждом шаге порция теплоты пересекает только одну границу между двумя соседними ячейками. Если найти мощности потоков теплоты через границы ячейки на момент начала шага и считать их в течение шага постоянными, то можно составить такую систему уравнений для расчета температур в конце шага, в каждом из которых будет только одно неизвестное. Такая схема решения называется явной и требует существенно меньшего объема вычислений по сравнению с неявной схемой, в каждом уравнении которой несколько неизвестных. На рис. 2.7 решение по явной схеме (1а) представляет собой ломаную линию, начало каждого отрезка которой параллельно касательной к кривой искомой функции. Видно, что эта ломаная с определенной точностью повторяет вид кривой.
Если шаг решения недостаточно мелкий, то предположение о сохранении постоянных тепловых потоков становится некорректным и приводит к неправильному решению (ломаная 16 удаляется от кривой). Максимально допустимый шаг во времени т пропорционален квадрату линейного размера самого мелкого элемента / и зависит от свойств материала (для тепловой задачи он обратно пропорционален коэффициенту температуропроводности а):
Поэтому при решении стационарных задач, как правило, выгоднее один раз составить и решить систему уравнений неявной схемы, чем выполнять большое число шагов явной схемы. Решение по неявной схеме (2) представлено на рис. 2.7 ломаной, составленной из секущих, начало и конец
Рис. 2.7. Работа явной (7) и неявной (2) схем решения при малом (о) и большом (б) шаге
каждого отрезка лежат на кривой. Порядок точности явной и неявной схем при мелком шаге одинаков. При увеличении шага при неявной схеме решение хотя и становится грубее, но остается устойчивым (ломаная 26 продолжает следовать за кривой). Погрешность при этом невелика, если функция меняется медленно. Таким образом, общее правило: явная схема — для нестационарных переходных процессов, где большое число шагов неизбежно, а неявная — для стационарных задач.
Напряженно-деформированное состояние. Расчет напряжений и деформаций во многом близок к расчету электрических потенциалов. За исключением явлений ползучести при высоких температурах и циклического или коррозионного роста трещин, процессы деформирования металла протекают достаточно быстро, чтобы задачи можно было считать стационарными. Сложность этих задач в том, что в каждой точке тела необходимо определить не скалярный параметр (потенциал, температуру), а вектор перемещения, имеющий величину и направление, т. е. число неизвестных для плоских моделей удваивается, а для объемных утраивается. Сложнее становится и описание потоков энергии через границы элементов. Более наглядной является их замена условиями равновесия. Каждое уравнение системы, полученной в соответствии с неявной схемой решения, можно трактовать как условие равновесия соответствующего узла модели в направлении одной из осей координат. В остальном все перечисленные выше положения,
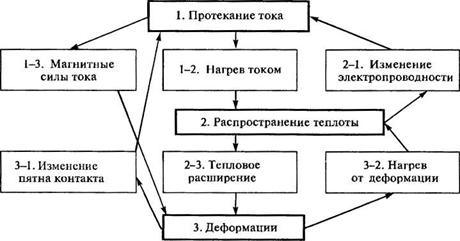
Рис. 2.8. Схема связей между процессами в металле при контактной сварке
включая граничные условия, нелинейность и т. д., в полной мере применимы и к этому несколько более сложному случаю.
Связные и несвязные задачи. Процессы, протекающие при сварке и эксплуатации конструкции, взаимосвязаны. Протекание тока вызывает нагрев и соответственно структурные и фазовые превращения и деформации от теплового расширения. Это не мешает моделировать процессы последовательно: вначале провести моделирование процесса протекания тока и записать его результаты, затем — моделирование распространения теплоты и т. д. Результаты, полученные на одной модели, входят в начальные и граничные условия и влияют на свойства материала в следующей модели. Такая последовательно решаемая задача называется несвязной. При ее решении пренебрегают обратными связями между процессами: влиянием нагрева на протекание тока, разогревом от пластической деформации и т. д.
Примером задач, которые необходимо решать как связные, являются задачи контактной сварки (рис. 2.8). Площадь и плотность контакта, через который протекает ток, существенно зависят от силы сжатия и деформации свариваемых деталей. В свою очередь, деформации зависят от изменения предела текучести и плавления металла при его нагреве проходящим током. Следовательно, все процессы необходимо моделировать синхронно, в рамках единой связной задачи.
Связная задача требует составления единой системы уравнений для нескольких взаимосвязанных процессов. Такой подход правильнее, но существенно сложнее в реализации. Выбор связной или несвязной задачи при моделировании должен быть сделан на основе оценки погрешности, вносимой неучетом обратных связей.
Достаточно полноценную, но менее сложную замену единой модели можно получить при итерационном решении, если моделировать процессы поочередно, но повторяя решение несколько раз и вводя поправки в каждую из моделей с учетом результатов, полученных на остальных моделях при предыдущей итерации. Сходимость, как и при решении нелинейных задач, зависит от степени влияния обратных связей на результаты решения.
Еще более простой алгоритм можно предложить при решении мелким шагом по явной схеме. Необходимо переходить от предыдущей модели к последующей не после завершения всего процесса моделирования, а на каждом шаге. Тогда обратные связи между процессами будут учтены, хотя и с запаздыванием на один шаг. При малом шаге будет получен результат, близкий к результату решения связной задачи.
🎥 Видео
Метод конечных элементов (Часть 1) | Пример реализации для уравнения теплопроводностиСкачать

Основы метода конечных элементов. Часть 1. Идея МКЭ в задачах конструкционного анализаСкачать

Метод конечных элементов. Основы 1.1.3 - Метод ГалеркинаСкачать
6-2. Метод сетокСкачать

Основы метода конечных элементов. Расчёт элементов фермСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Метод конечных элементовСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Метод конечных элементов (FEM) vs метод контрольного объёма (FVM). В чём разница?Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение уравнения теплопроводности методом конечных разностейСкачать

РК6. Модели и методы анализа проектных решений. Метод конечных элементов: основные положенияСкачать

Метод конечных элементов. Основы 1.1.2 - Метод коллокацийСкачать

Метод конечных элементов. Как получить матрицу жесткости. Начало.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать