для обыкновенных дифференциальных уравнений.
Примером краевой задачи является двухточечная краевая задача для обыкновенного дифференциального уравнения второго порядка:
с граничными условиями, заданными на концах отрезка [a; b]:
Следует найти такое решение у(х) на этом отрезке, которое принимает на концах отрезка значения у0, у1. Если функция 

Кроме граничных условий, задаваемых на концах отрезка и называемых граничными условиями первого рода, используются еще условия на производные от решения на концах — граничные условия второго рода:
или линейная комбинация решений и производных – граничные условия третьего рода:
где 
Возможно на разных концах отрезка использовать условия различных типов.
Наиболее распространены два приближенных метода решения краевой задачи:
— метод стрельбы (пристрелки);
Используя конечно-разностный метод, рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения второго порядка на отрезке [а; b].
Введем разностную сетку на отрезке [а; b]:
Решение задачи будем искать в виде сеточной функции:
предполагая, что решение существует и единственно.
Введем разностную аппроксимацию производных следующим образом:
Подставляя эти аппроксимации производных в исходное уравнение, получим систему уравнений для нахождения yk:
Приводя подобные члены и учитывая, что при задании граничных условий первого рода два неизвестных уже фактически определены, получим систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов:
Для этой системы уравнений при достаточно малых шагах сетки h и q(xk)
В первом случае линейная алгебраическая система аппроксимирует дифференциальную задачу в целом только с первым порядком (из-за аппроксимации в граничных точках), однако сохраняется трех диагональная структура матрицы коэффициентов. Во втором случае второй порядок аппроксимации сохраняется везде, но матрица линейной системы не трехдиагональная.
Пример. Решить краевую задачу:
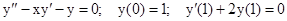
Во всех внутренних узлах отрезка [0; 1] после замены производных их разностными аналогами получим:
На левой границе y0 = 1, на правой границе аппроксимируем производную односторонней разностью 1-го порядка:
С помощью группировки слагаемых, приведения подобных членов и подстановки значений xk, а также с учётом у0 = 1,получим систему линейных алгебраических уравнений:

В результате решения системы методом Крамера в Excel, получим:
Решением краевой задачи является табличная функция:
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| xk | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| yk | 1,0 | 0,772 | 0,583 | 0,431 | 0,313 | 0,223 |
Расчетная часть
3.1. Найти действительные корни уравнения 
Решение: Для нахождения корня уравнения предварительно отделим корень уравнения графическим методом, записав уравнение в виде:
Построим в осях ХОУ графики функций:

Линии графиков пересекаются в единственной точке с абсциссой х0, лежащей в интервале [0,5; 0,6], т.е.
Значение функции 
Т.к. знаки различны, то уравнение имеет единственный корень в интервале [0,5; 0,6].
3.1.1. Уточнение корня методом простых итераций.
Приведём исходное уравнение к виду:
Т.к. первая производная заданной функции 
Т.о. итерационная функция приобретает вид:
Делаем первую итерацию:
Делаем вторую итерацию:
Делаем третью итерацию:
Делаем четвёртую итерацию:
Делаем пятую итерацию:
Делаем шестую итерацию:
Делаем седьмую итерацию:
Делаем восьмую итерацию:
Делаем девятую итерацию:
Продолжая далее, получаем:
На 19-ой итерации изменение шестого знака после запятой, позволяет утверждать, что пятый знак – после запятой – 5. Т.о. значение корня с заданной точностью:
3.1.2. Уточнение корня методом касательных (метод Ньютона):
Т.к. уравнение то же, то интервал, содержащий искомый корень, оставляем тот же [0,5; 0,6], т.е. а = 0,5; b = 0,6.
Находим первую и вторую производную функции 
Очевидно необходимые условия выполняются, т.к.:


Выполняем первое приближение (х0 = 0,5):
Выполняем второе приближение (х1 = 0,571429):
Выполняем третье приближение (х2 = 0,576128:
Выполняем четвёртое приближение (х3 = 0,576146):
В пределах заданной точности f(x2) оказался равен нулю, т.е. требуемая точность достигнута за 4 шага. Значение корня с заданной точностью:
3.2. Вычислить приближенное значение интеграла 
а) трапеций (n = 10); б) Симпсона (n = 10); в) Гаусса (n = 5).
Решение: Ограничимся в расчётах 4 знаками после запятой. Для приближённого вычисления определённого интеграла методом трапеций используется формула:
Разобьём интервал (–1; 9) на n = 10 отрезков (h =1) и вычислим значения подынтегрального выражения для начала и конца каждого отрезка.
| № | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 | 2,4495 | 2,6458 | 3,7417 | 5,7446 | 8,3666 | 11,4455 | 14,8997 | 18,6815 | 22,7596 | 27,1109 | 31,7175 |
Тогда по формуле трапеций, имеем:
Используя формулу Симпсона (формулу параболических трапеций) в виде:

Применяя к исходному интегралу квадратурную формулу Гаусса, имеем:
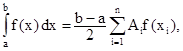
Для n = 5, коэффициенты ti, представляющие нули полинома Лежандра и коэффициента Аi (эти значения табулированы в справочных таблицах) составляют:
| i | 1 | 2 | 3 | 4 | 5 |
| ti | –0,9061 | –0,5385 | 0 | 0,5385 | 0,9061 |
| A1 | 0,2369 | 0,4786 | 0,5689 | 0,4786 | 0,2369 |
| хi | 0,4695 | 2,3075 | 5 | 7,6925 | 9,5305 |
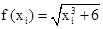 | 2,4705 | 4,2763 | 11,4455 | 21,4756 | 29,5239 |
3.3. Построить интерполяционные многочлены Лагранжа и Ньютона по следующим табличным данным:
 | 2,9 | 4,4 | 6,3 | 9,7 |
 | 2,84 | 4,53 | 6,04 | 5,50 |
Проверить совпадение значений интерполирующего многочлена с табличными значениями функции в узлах интерполяции.
Решение: Интерполяционный полином Лагранжа для четырёх узлов интерполяции записывается в виде:
Подставим численные значения из заданной таблицы:
Для составления интерполяционного полинома в форме Ньютона, вычислим разности первого порядка для заданной таблицы по формуле:
Вычислим разности второго порядка по формуле:
Вычислим разность третьего порядка по формуле:
Тогда интерполяционный полином Ньютона Ln(x) приобретает следующую форму:
Расчёты показывают, что оба интерполяционных полинома практически одинаковы, т.е. интерполяция ряда точек полиномом третьей степени осуществляется единственным образом.
По заданным узлам интерполяции хi значения полинома по этому уравнению составляют:
| х | 2,9 | 4,4 | 6,3 | 9,7 |
| Ln(x) | 2,840133 | 4,530614 | 6,041651 | 5,504897 |
| f(x) | 2,84 | 4,53 | 6,04 | 5,50 |
Расчётные значения практически совпадают с заданными значениями f(x).
По полученному уравнению построена кривая, проходящая через узлы интерполяции.
3.4. Найти оценки параметров линейной 



 | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 |
 | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 |
Построить чертеж: на плоскости нанести экспериментальные точки 

Решение: Коэффициенты «a0 и а1» линейной модели найдём, выполнив необходимые вычисления. Расчеты сведем в таблицу:
| Номер наблюдения | 1 | 2 | 3 | 4 | 5 | Сумма |
| х | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 | 16 |
| у | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 | 11,2 |
| х 2 | 0,16 | 5,76 | 11,56 | 19,36 | 29,16 | 66 |
| х∙y | 0,856 | 5,136 | 7,616 | 10,296 | 12,636 | 36,54 |
 | 2,108 | 2,202 | 2,249 | 2,297 | 2,344 | 11,200 |
 | 0,0011 | 0,0039 | 0,0001 | 0,0019 | 0,0000 | 0,0069 |
Т.о. линейная зависимость у = а0 + а1х имеет вид: у = 2,08865 + 0,0473х.
По этой зависимости определены выровненные значения 
Коэффициенты а0, а1, а2 квадратичной зависимости найдём, также выполнив необходимые расчёты в таблице:
| Номер наблюдения | 1 | 2 | 3 | 4 | 5 | S |
| х | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 | 16 |
| у | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 | 11,2 |
| х 2 | 0,16 | 5,76 | 11,56 | 19,36 | 29,16 | 66 |
| х 3 | 0,064 | 13,824 | 39,304 | 85,184 | 157,464 | 295,84 |
| х 4 | 0,0256 | 33,1776 | 133,634 | 374,81 | 850,306 | 1391,95 |
| у·х | 0,856 | 5,136 | 7,616 | 10,296 | 12,636 | 36,54 |
| у·х 2 | 0,3424 | 12,3264 | 25,8944 | 45,3024 | 68,2344 | 152,1 |
 | 2,128 | 2,182 | 2,230 | 2,292 | 2,368 | 11,200 |
 | 0,0001 | 0,0018 | 0,0001 | 0,0023 | 0,0008 | 0,0051 |
Составим систему уравнений:
Решение этой системы методом Крамера даёт:
Т.о. квадратичная зависимость у = а0 + а1х + а2х 2 имеет вид:
у = 2,12433 + 0,00729·х + 0,006996·х 2 .


Эмпирическая ломаная, а также линии линейной и квадратичной модели построены на рисунке.
Результаты и выводы.
1. Т.о. интерполяционный полином Лагранжа и Ньютона, построенный по 4 заданным узлам интерполяции имеет вид:
Значения функции, вычисленные по этому полиному третьей степени, точно совпадают с заданными значениями в узлах интерполяции.
Полученное уравнение позволяет найти приближённые значения функции в любых промежуточных точках от х1 = 2,9 до х4 = 9,7.
2. Применение метода минимальных квадратов (МНК) к аппроксимации пяти экспериментальных точек линейной зависимостью вида у = а0 + а1х, т.е. прямой линией и квадратичной зависимостью вида 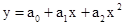
– линейная зависимость реализована уравнением: у = 2,0887 + 0,0473х
– квадратичная зависимость реализована уравнением: у = 2,1243 + 0,0073·х + 0,007·х 2 .
Судя по остаточной сумме квадратов отклонений, квадратичная зависимость несколько лучше аппроксимирует экспериментальные данные, т.к. для неё остаточная сумма квадратов отклонений меньше, чем для линейной функции.
Список использованной литературы
1. Самарский А.А. Гулин А.В. Численные методы. М. МГУ. 1989 год.
2. Н. С. Бахвалов; Н.П. Жидков; Г.М. Кобельков. Численные методы. М 2003 год;
3. В.А. Буслов, С.Л.Яковлев. Численные методы и исследование функций. СПГУ. Курс лекций. СПБ 2001 г
4. Г.А. Зуева. Метод наименьших квадратов и его применение. Электронное учебное пособие. Иваново, 2009
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа
| Название: Конечно-разностный метод решения для уравнений параболического типа Раздел: Рефераты по математике Тип: контрольная работа Добавлен 23:16:39 16 апреля 2011 Похожие работы Просмотров: 16037 Комментариев: 20 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| xi | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| ti | |||||||||||
| 0 | 0 | 1.1180 | 1.5388 | 1.1180 | 0.3633 | 0 | 0.3633 | 1.1180 | 1.5388 | 1.1180 | 0 |
| 0.01 | 0 | 0.6169 | 0.9288 | 0.8621 | 0.6177 | 0.4905 | 0.6177 | 0.8621 | 0.9288 | 0.6169 | 0 |
| 0.02 | 0 | 0.3942 | 0.6480 | 0.7186 | 0.6800 | 0.6488 | 0.6800 | 0.7186 | 0.6480 | 0.3942 | 0 |
| 0.03 | 0 | 0.2887 | 0.5067 | 0.6253 | 0.6665 | 0.6733 | 0.6665 | 0.6253 | 0.5067 | 0.2887 | 0 |
| 0.04 | 0 | 0.2331 | 0.4258 | 0.5560 | 0.6251 | 0.6458 | 0.6251 | 0.5560 | 0.4258 | 0.2331 | 0 |
| 0.05 | 0 | 0.1995 | 0.3720 | 0.4996 | 0.5754 | 0.6002 | 0.5754 | 0.4996 | 0.3720 | 0.1995 | 0 |
| 0.06 | 0 | 0.1759 | 0.3315 | 0.4511 | 0.5253 | 0.5504 | 0.5253 | 0.4511 | 0.3315 | 0.1759 | 0 |
| 0.07 | 0 | 0.1574 | 0.2981 | 0.4082 | 0.4778 | 0.5015 | 0.4778 | 0.4082 | 0.2981 | 0.1574 | 0 |
| 0.08 | 0 | 0.1419 | 0.2693 | 0.3698 | 0.4338 | 0.4558 | 0.4338 | 0.3698 | 0.2697 | 0.1419 | 0 |
| 0.09 | 0 | 0.183 | 0.2437 | 0.3351 | 0.3936 | 0.4137 | 0.3936 | 0.3351 | 0.2437 | 0.1283 | 0 |
| 0.1 | 0 | 0.1161 | 0.2208 | 0.3038 | 0.3570 | 0.3753 | 0.3570 | 0.3038 | 0.2208 | 0.1161 | 0 |
Величины, полученные методом Кранка-Николсона, достаточно близки к
аналитическому решению u(x,t) = sin(πx)e -π2 t + sin(3πx)e -9π2 t , истинные значения для последнего представлены в таблице 2
Максимальная погрешность для данных параметров равна 0,005
Таблица 2 – точные значения u(х i , ti ), при t=0.1
| xi | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| t11 | |||||||||||
| 0.1 | 0 | 0.1153 | 0.2192 | 0.3016 | 0.3544 | 0.3726 | 0.3544 | 0.3016 | 0.2192 | 0.1153 | 0 |
Рисунок 5 –Решениеu= u(х i , ti ), для метода Кранка-Николсона
В зависимости от формы области, краевых условий, коэффициентов исходного уравнения метод конечных разностей имеет погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов.
В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в около граничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций.
Проблемой методов конечных разностей является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах. Поэтому реализация методов конечных разностей в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.
1 Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.
2 Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB, 3-е издание.— М. : Вильяме, 2001. — 720 с
3 Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.
4 Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004. — 400 с.
5 Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.
6 Калиткин Н.Н. Численные методы. – М.: Наука, 1976.
Листинг программы для расчета по методу Кранка-Николсона
Видео:6.3 Решение разностных уравненийСкачать

Методы конечных разностей
Достоинство этих методов состоит в том, что они сводят решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается заменой производных, входящих в дифференциальное уравнение, их конечно-разностными аппроксимациями.
Рассмотрим сущность такого метода решения для дифференциального уравнения второго порядка (1.41) при заданных граничных условиях (1.42). Разобьем отрезок [0,1] на n равных частей точками xi= ih(i= 0,1. , n). Решение краевой задачи (1.41), (1.42) сведем к вычислению значений сеточной функции yi в узловых точках xi. Для этого напишем уравнение (1.42) для внутренних узлов:

Заменим производные, входящие в эти соотношения, их конечно-разностными аппроксимациями:


Подставляя эти выражения в (1.49), получаем систему разностных уравнений:

являющуюся системой n-1 алгебраических уравнений относительно значений сеточной функции 
На практике часто граничные условия задают в более общем виде (1.38):

В этом случае граничные условия также должны представляться в разностном виде путем аппроксимации производных Y‘(0) и Y‘(1) с помощью конечно-разностных соотношений. Если использовать односторонние разности (соответствующий шаблон показан на рис. 1.7, а),при которых производные аппроксимируются с первым порядком точности, то разностные граничные условия примут вид

Из этих соотношений легко находятся значения y0, yn.
Однако, как правило, предпочтительнее аппроксимировать производные, входящие в (1.52), со вторым порядком точности с помощью центральных разностей:
Рис. 1.7. Аппроксимация граничных условий
В данные выражения входят значения сеточной функции 
Аппроксимировать граничные условия со вторым порядком можно и иначе (см. рис. 1.7, в). В этом случае используют аппроксимации:
Таким образом, решение краевой задачи для дифференциального уравнения сведено к решению системы алгебраических уравнений вида (1.51). Эта система является линейной или нелинейной в зависимости от того, линейно или нелинейно дифференциальное уравнение (1.41). Методы решения таких систем рассмотрены ранее.
Рассмотрим подробнее один частный случай, который представляет интерес с точки зрения практических приложений и позволяет проследить процесс построения разностной схемы. Решим краевую задачу для линейного дифференциального уравнения второго порядка

с граничными условиями вида
Разобьем отрезок [0,1] на части с постоянным шагом h с помощью узлов 
Обозначим рi, fiсоответственно величины 

Получилась система n—1 линейных уравнений, число которых совпадает с числом неизвестных значений сеточной функции 
Решив систему уравнений (1.56) с учетом условий (1.57), найдем значения сеточной функции, которые приближенно равны значениям искомой функции. Покажем, что такое решение существует и сходится к точному решению при h→ 0.
Для доказательства существования решения рассмотрим систему линейных уравнений (1.56). Ее матрица является трехдиагональной; на главной диагонали находятся элементы 
Что касается сходимости решения, то здесь имеет место следующее утверждение.
Утверждение. Если функции р(х) и f(x) дважды непрерывно дифференцируемы, то при h→0 разностное решение равномерно сходится к точному со скоростью O(h2).
Это — достаточное условие сходимости метода конечных разностей для краевой задачи (1.54), (1.55).
Система линейных алгебраических уравнений (1.56) с трехдиагональной матрицей может быть решена методом прогонки. При этом условие р(х) > 0 гарантирует выполнение условия устойчивости прогонки.
Этот метод на практике используется также и при р(х) Будет полезно почитать по теме:
📺 Видео
6-2. Метод сетокСкачать

Разностные уравнения | Решение задачСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение систем уравнений методом подстановкиСкачать

Решение биквадратных уравнений. 8 класс.Скачать

11 класс, 27 урок, Общие методы решения уравненийСкачать

Методы решения нелинейных краевых задач для ОДУСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Метод решения уравнений, чтобы не ошибаться в знакахСкачать

Система уравнений. Метод алгебраического сложенияСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Конечно-разностные методыСкачать









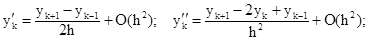






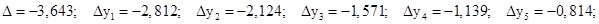












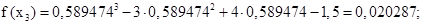

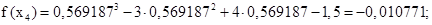















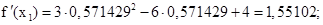



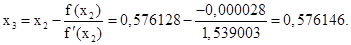








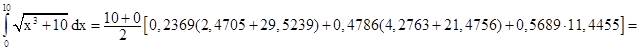


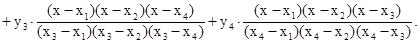

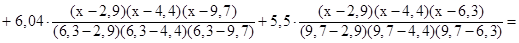









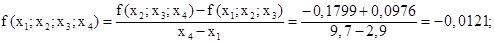
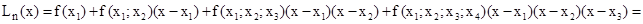










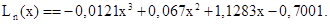
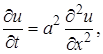
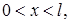
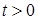 (1)
(1)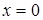 и
и 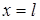 заданы значения искомой функции
заданы значения искомой функции 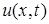 в виде
в виде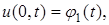
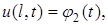
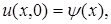
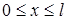 ,
, 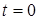 , (4)
, (4)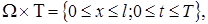 a 2 — коэффициент температуропроводности, а (2), (3) с помощью функций
a 2 — коэффициент температуропроводности, а (2), (3) с помощью функций 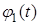 ,
, 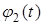 задают температуру на границах
задают температуру на границах 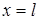 заданы значения производных искомой функции по пространственной переменной:
заданы значения производных искомой функции по пространственной переменной: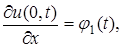
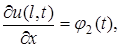
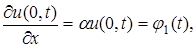
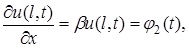
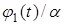 на границе
на границе 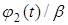 на границе
на границе 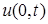 ,
, 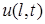 . Коэффициенты α, β – известные коэффициенты теплообмена между газообразной или жидкой средой и соответствующей границей.
. Коэффициенты α, β – известные коэффициенты теплообмена между газообразной или жидкой средой и соответствующей границей.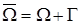 первая начально-краевая задача имеет вид
первая начально-краевая задача имеет вид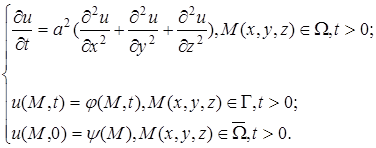 (9)
(9)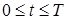 конечно разностную сетку ωh,τ :
конечно разностную сетку ωh,τ :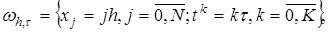 (10)
(10)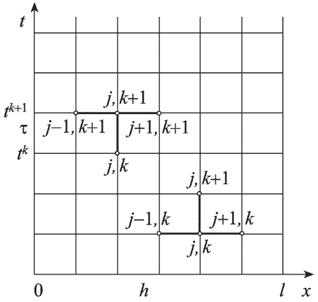
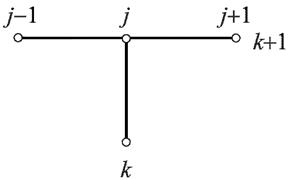
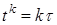 ,на котором распределение искомой функции u ( xj , t k ) ,
,на котором распределение искомой функции u ( xj , t k ) , 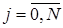 , известно (при к = 0 распределение определяется начальным условием (4)u ( xj , t k )=ψ( xj ) ), и верхний временной слой t k +1 =( k +1) τ , на котором распределение искомой функции u ( xj , t k +1 ) ,
, известно (при к = 0 распределение определяется начальным условием (4)u ( xj , t k )=ψ( xj ) ), и верхний временной слой t k +1 =( k +1) τ , на котором распределение искомой функции u ( xj , t k +1 ) , 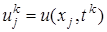 .
.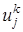 ,
, 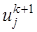 первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают
первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают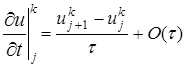 , (11)
, (11)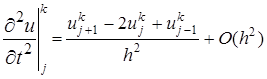 , (12)
, (12)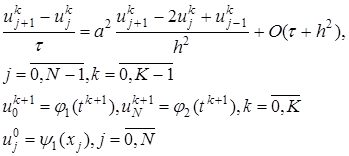 (13)
(13)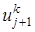 , которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j =1 и j = N — l , a начальное условие – при k = 0.
, которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j =1 и j = N — l , a начальное условие – при k = 0.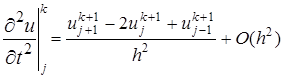 , (14)
, (14)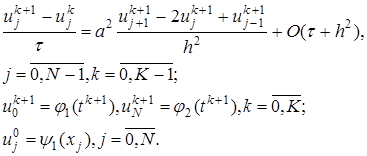 (15)
(15)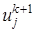 на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид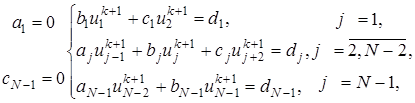
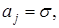
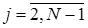 ;
;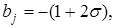
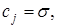 ,
, 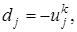
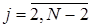 ;
;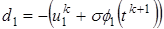 ;
;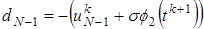 ;
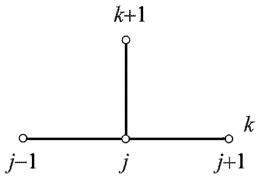
;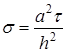 .
.
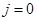 , чтобы в дальнейшем последовательно определять значения решения в узлах слоев
, чтобы в дальнейшем последовательно определять значения решения в узлах слоев 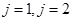 и т.д. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.
и т.д. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.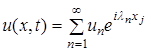 , (16)
, (16)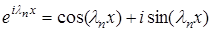 – собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник
– собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник 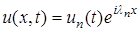 , каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x .
, каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x .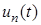 , называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.
, называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.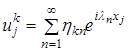 (17)
(17)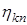 может быть представлена в виде произведения
может быть представлена в виде произведения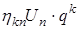 (18)
(18)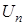 – размерный и постоянный сомножитель амплитудной части,
– размерный и постоянный сомножитель амплитудной части,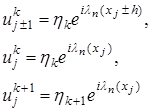 (19)
(19)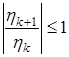 , (20)
, (20)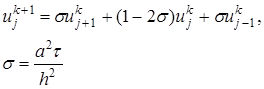 (21)
(21)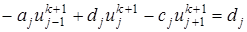 (22)
(22)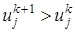 . Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как
. Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как 
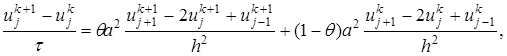 (23)
(23)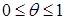 . При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона .
. При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона .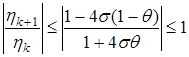 ,
,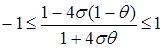 (24)
(24)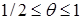 . Если же вес θ лежит в пределах
. Если же вес θ лежит в пределах 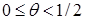 , то между σ и θ из левого неравенства устанавливается связь
, то между σ и θ из левого неравенства устанавливается связь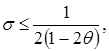
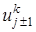 ,
, 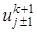 по переменной х и полученные разложения подставим в (23):
по переменной х и полученные разложения подставим в (23):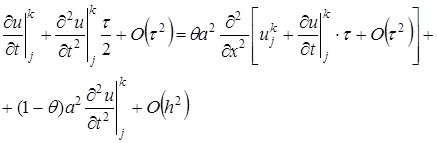
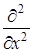 от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору
от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору 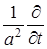 , в соответствии с чем вышеприведенное равенство приобретает вид
, в соответствии с чем вышеприведенное равенство приобретает вид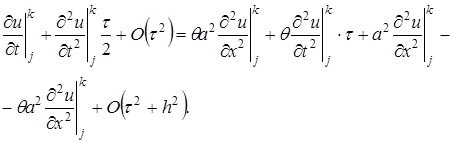
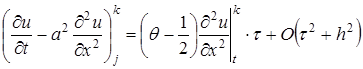 ,
,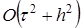 , т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х .
, т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х .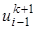 ,
, 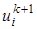 , и
, и 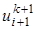 . Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу
. Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу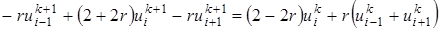 (26)
(26)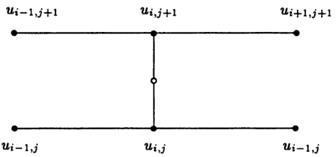
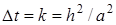 , формула (26) упрощается и принимает вид
, формула (26) упрощается и принимает вид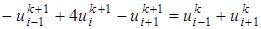 , (27)
, (27)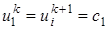 и
и 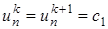 соответственно).
соответственно).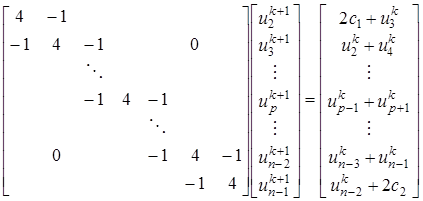
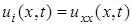 ,
,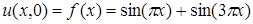 ,
,