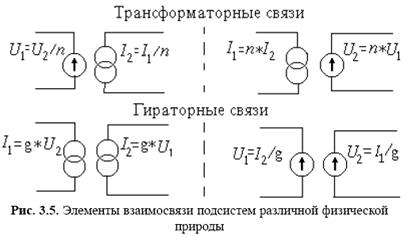
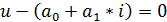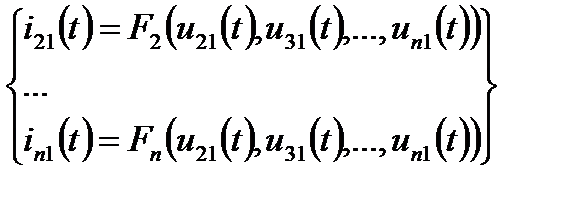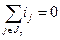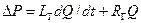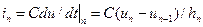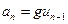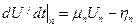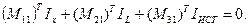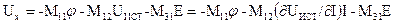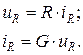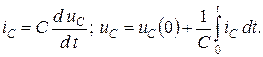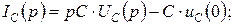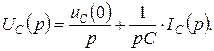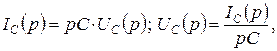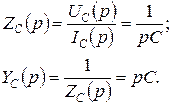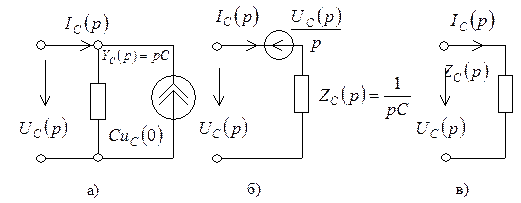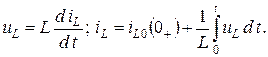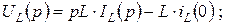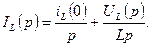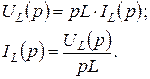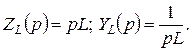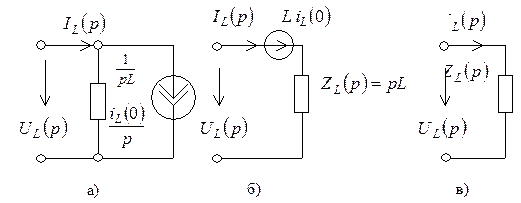Закономерности, описывающие поведение элементов цепи (элементные или компонентные законы)
Это математические выражения, связывающие между собой переменные, описывающие состояние элемента – токи через выводы элемента и напряжения между выводами этого элемента. Такие математические уравнения называют элементными или компонентными законами. Такие законы могут иметь вид алгебраических или дифференциальных уравнений. Количество таких уравнений для элемента с n выводами равно (n‑1).
Простейший вид элемента – с двумя выводами (двухполюсник). Его поведение описывается зависимостью между двумя величинами: iиu. Ее называют вольт-амперной характеристикой ВАХ.
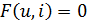
С математической точки зрения – любая.
Как можно определить ВАХ экспериментально? Изменяя одну из величин и измеряя обе.
Элемент называют линейным, если ВАХ – полином первого порядка
Может ли быть так, что при заданном значении аргумента 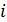
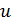
Может ли быть так, что при постоянном значении аргумента 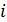
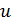
Пример с конденсатором.
Пример с термозависимым резистором (саморазогрев).
Пример с диодом – нелинейный элемент
Эксперимент по снятию ВАХ резистора и полупроводникового диода а) вручную, б) с помощью характериографа
Простой вариант формирования системы компонентных уравнений для n-полюсника:
· Выбрать один из выводов в качестве базового.
· Задать величины напряжений между каждым из оставшихся и базовым выводом (возможность этого является следствием второго закона Кирхгофа).
· Измерять токи через каждый из выводов за исключением базового.
Система из (n-1) уравнений, описывающая поведение n-полюсника будет иметь вид
здесь F символизирует зависимость, которая может быть алгебраической, либо содержать производные и (или) интегралы переменных u(t) и i(t).
Энергетические свойства элементов электрических цепей.
Диссипативность: (необратимое) превращение электрической энергии в тепло
Переход части электрической энергии в тепло при протекании тока по диссипативным элементам. Компонентное уравнение диссипативного элемента цепи. Потери энергии в электронных информационных устройствах. Почему энергия не может быть сколь-угодно малой.
Большая группа элементов цепей обладает свойством, состоящим в том, что вся энергия, доставляемая токами, протекающими через выводы, превращается внутри таких элементов в тепло. Такие элементы называют диссипативными[2]. Примером такого элемента является резистор, используемый в электронных цепях для …. () Компонентное уравнение диссипативного двухполюсника имеет вид
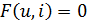
Запись уравнения в таком виде подчёркивает тот факт, что ни одна из двух переменных 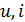
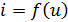
Однако утверждение о «первичности» напряжения ошибочно.
Характеристики диссипативных элементов часто называют «вольт-амперными», поскольку в выражении присутствуют две переменные: напряжение 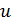
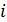
Вольт-амперная характеристика 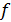
Для металлических проводников компонентная зависимость весьма близка к прямой пропорциональной ‑ это всем известный «закон Ома» 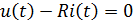
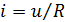
В электротехнических устройствах используются многочисленные элементы с числом выводов, превышающим два. Прежде всего, это транзисторы, у которых три вывода (у некоторых полевых транзисторов может быть четыре вывода). Вольт-амперные характеристики многополюсных диссипативных элементов представляют собой семейство функций нескольких аргументов. Количество функций, а также количество аргументов в каждой функции на единицу меньше количества выводов многополюсника.
Емкость: (обратимое) накопление энергии в электрическом поле (заряженного конденсатора).
Запасание части электрической энергии в реактивных элементах цепи ‑ в виде энергии электрического поля в конденсаторе или в виде энергии магнитного поля в индукторе. Компонентные уравнения реактивных элементов (накопителей энергии).
Некоторые виды элементов цепей способны обратимо накапливать электрическую энергию в электрическом или в магнитном поле.
Компонентное уравнение элемента цепи, способного накапливать энергию в электрическом поле (электростатического накопителя), в общем случае имеет вид
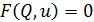
Это соотношение иногда называют «вольт-кулонной» характеристикой. Однако при описании электрической цепи, содержащей электростатический накопитель, состояние цепи описывают, используя только напряжения и токи (и, может быть, их производные и интегралы). Этого можно достигнуть, использовав соотношение между зарядом и током (используемого в определении единицы заряда 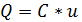
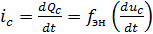
Любой фрагмент электрической цепи, в котором имеются две точки, между которыми существует ненулевое напряжение, обладает свойствами электростатического накопителя. Вид функции 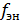
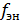
Для большинства веществ функция 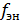
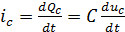
В последней формуле 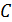
Изготавливаются и используются в электрических цепях конденсаторы – двухполюсники, обладающие свойством электростатического накопителя. При проектировании и изготовлении конденсаторов принимают специальные меры для обеспечения постоянства величины их емкости.
Конденсатор, заряженный до напряжения 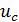
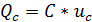
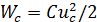
а) скорость изменения напряжения на электростатическом накопителе тем больше, чем больше величина перезаряжающего тока,
б) напряжение на электростатическом накопителе не может измениться скачком, поскольку для этого необходим ток бесконечно большой величины, что физически не реализуемо.
Индуктивность: (обратимое) накопление энергии в магнитном поле тока.
Компонентное уравнение элемента цепи, способного накапливать энергию в магнитном поле (электромагнитного накопителя), имеет вид:
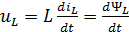
Соотношение (2.9) иногда называют «вебер-амперной характеристикой», поскольку оно устанавливает связь между величиной суммарного магнитного потока (потокосцепления) и величиной тока, создающего этот поток. Величина потокосцепления 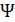
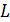
Любой фрагмент реальной электрической цепи в некоторой степени обладает свойствами магнитного накопителя, поскольку вокруг проводника с током всегда возникает магнитное поле.
Из формулы вебер-амперной характеристики (2.9) следуют важные для дальнейшего изложения выводы
а) скорость изменения тока в электромагнитном накопителе тем больше, чем больше величина напряжения между его выводами,
б) ток в магнитном накопителе не может измениться скачком, поскольку для этого напряжение между выводами магнитного накопителя должно стать бесконечно большим, что физически не реализуемо.
Для линейных двухполюсников математическое выражение этих свойств:
Резистивность (диссипативность): 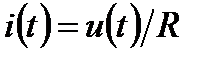
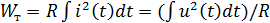
это соотношение известно как Закон Ома – ВАХ идеального резистора
Емкость электрическая 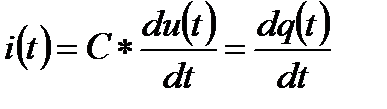
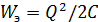
вольт-кулонная характеристика электростатического накопителя энергии
Индуктивность 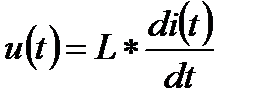
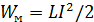
вебер-амперная характеристика электромагнитного накопителя энергии
Два последних соотношения никак не называются, хотя все три формулы представляют собой простейшие математические модели для трех видов двухполюсников: резистора, конденсатора и катушки индуктивности (индуктора).
Любой реальный двухполюсник обладает всеми тремя свойствами, только в разной степени.
В каких случаях можно пренебречь отдельными свойствами. На этот вопрос можно ответить, проведя анализ энергетического баланса.
Видео:Олимпиадная задача по ТОЭ #1. Активные двухполюсники│Постоянный токСкачать

Математические модели в процедурах анализа на макроуровне
Исходные уравнения моделей.Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели. В этом параграфе изложен обобщенный подход к формированию алгоритмических моделей на макроуровне, справедливый для большинства приложений.
Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.
Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов (ММЭ).
Топологические уравнения описывают взаимосвязи в составе моделируемой системы.
В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).
Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.
В перечисленных выше приложениях компонентные уравнения имеют вид:
и топологические уравнения
Различают фазовые переменные двух типов, их обобщенные наименования – фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение – связи между однотипными фазовыми переменными в разных компонентах.
Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.
Примеры компонентных и топологических уравнений.Рассмотрим несколько типов систем.
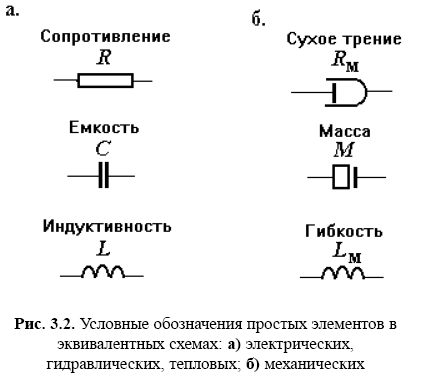
Электрические системы. В электрических системах фазовыми переменными являются электрические напряжения и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные двух- и многополюсные компоненты. К простым двухполюсникам относятся следующие элементы: сопротивление, емкость и индуктивность, характеризуемые одноименными параметрами R, С, L. В эквивалентных схемах эти элементы обозначают в соответствии с рис. 3.2,а.
Компонентные уравнения простых двухполюсников:
для R: u = i R (закон Ома), (3.3)
для C: i = C du/dt, (3.4)
для L: u = L di/dt, (3.5)
где и – напряжение (точнее, падение напряжения на двухполюснике), i – ток.
Эти модели лежат в основе моделей других возможных более сложных компонентов. Большая сложность может определяться нелинейностью уравнений (3.3) – (3.5) (т.е. зависимостью R, С, L от фазовых переменных), или учетом зависимостей параметров R, С, L от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.
Топологические уравнения выражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:
где Кр – множество номеров элементов р-гоконтура, Jq – множество номеров элементов, входящих в q-есечение.
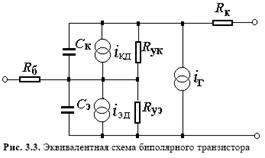
Примером ММ сложного компонента может служить модель транзистора. На рис. 3.3 представлена эквивалентная схема биполярного транзистора, на которой зависимые от напряжений источники тока iэд = iтэехр(uэ/(mφT)) и iкд = iткехр(uк/(mφT)) отображают статические вольтамперные характеристики p-n переходов, iтэ и iтк – тепловые токи переходов, mφT – температурный потенциал, иэ и ик_ напряжения на эмиттерном и коллекторном переходах, Сэ и Ск – емкости переходов, Rуэ и Rук – сопротивления утечки переходов, R6 и RK – объемные сопротивления тел базы и коллектора, iг = Biэд– Bиiкд _источник тока, моделирующий усилительные свойства транзистора, В и Ви – прямой и инверсный коэффициенты усиления тока базы. Здесь иэ, ик, iэд, iкд, iг– фазовые переменные, а остальные величины – параметры модели транзистора.
Механические системы. Фазовыми переменными в механических поступательных системах являются силы и скорости. Используют одну из двух возможных электромеханических аналогий. В дальнейшем будем использовать ту из них, в которой скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока. Учитывая формальный характер подобных аналогий, в равной мере можно применять и противоположную терминологию.
Компонентное уравнение, характеризующее инерционные свойства тел, в силу второго закона Ньютона имеет вид
F= M du/dt (3.8)
где F – сила; M – масса; u – поступательная скорость.
Упругие свойства тел описываются компонентным уравнением, которое можно получить из уравнения закона Гука. В одномерном случае (если рассматриваются продольные деформации упругого стержня)
где G – механическое напряжение; Е – модуль упругости; ε = Δl/l – относительная деформация; Δl – изменение длины l упругого тела под воздействием G. Учитывая, что G = F/S, где F – сила, S – площадь поперечного сечения тела, и дифференцируя (3.9), имеем
где g =(SE/l)- жесткость (величину, обратную жесткости, называют гибкостью LM); и = d(Δl)/dt – скорость.
Диссипативные свойства в механических системах твердых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причем в этих соотношениях производные сил или скоростей не фигурируют, как и в случае описания с помощью закона Ома диссипативных свойств в электрических системах.
Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера), во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.
В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных скоростей на угловые, сил – на вращательные моменты, масс – на моменты инерции, жесткостей – на вращательные жесткости.
Условные обозначения простых элементов механической системы показаны на рис. 3.2,б.
Нетрудно заметить наличие аналогий между электрической и механической системами. Так, токам и напряжениям в первой из них соответствуют силы (либо моменты) и скорости механической системы, компонентным уравнениям (3.4) и (3.5) и фигурирующим в них параметрам С и L, – уравнения (3.8) и (3.10) и параметры М и LM, очевидна аналогия и между топологическими уравнениями. Далее параметры С и М будем называть емкостными (емкостного типа), параметры L и LM – индуктивными (индуктивного типа), а параметры R и Rтр = 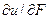
Имеется и существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих, соответствующих шести степеням свободы.
Однако отмеченные выше аналогии остаются справедливыми, если их относить к проекциям сил и скоростей на каждую пространственную ось, а при графическом представлении моделей использовать шесть эквивалентных схем – три для поступательных составляющих и три для вращательных.
Гидравлические системы. Фазовыми переменными в гидравлических системах являются расходы и давления. Как и в предыдущем случае, компонентные уравнения описывают свойства жидкости рассеивать или накапливать энергию.
Рассмотрим компонентные уравнения для жидкости на линейном участке трубопровода длиной Δl и воспользуемся уравнением Навье-Стокса в следующей его форме (для ламинарного течения жидкости)
где р – плотность жидкости; U– скорость; Р – давление; а – коэффициент линеаризованного вязкого трения. Так как U = Q/S, где Q – объемный расход; S – площадь поперечного сечения трубопровода, то, заменяя пространственную производную отношением конечных разностей, имеем
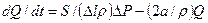
где ΔР – падение давления на рассматриваемом участке трубопровода. Lг= Δlρ/S – гидравлическая индуктивность, отражающая инерционные свойства жидкости, Rг= 2a/ρ – гидравлическое сопротивление, отражающее вязкое трение.
Примечание.В трубопроводе круглого сечения радиусом r удобно использовать выражение для гидравлического сопротивления при ламинарном течении: Rг = δυΔl/πr 4 ), где υ – кинематическая вязкость; в случае турбулентного характера течения жидкости компонентное уравнение для вязкого трения имеет вид 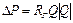
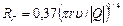
Интерпретация уравнения (3.11) приводит к эквивалентной схеме рис. 3.4.
Явление сжимаемости жидкости описывается компонентным уравнением, вытекающим из закона Гука
Дифференцируя (3.12) и учитывая, что объемный расход Q связан со скоростью U= d(Δl)/dt соотношением Q = U S, получаем
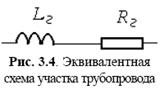
Связь подсистем различной физической природы. Используют следующие способы моделирования взаимосвязей подсистем: с помощью трансформаторной, гираторной связей и с помощью зависимости параметров компонентов одной подсистемы от фазовых переменных другой. В эквивалентных схемах трансформаторные и гираторные связи представлены зависимыми источниками фазовых переменных, показанными на рис. 3.5. На этом рисунке k и п – коэффициенты трансформации; g – передаточная проводимость; Uj и Ij ,- фазовые переменные в j-й цепи; j=1 соответствует первичной, а j=2 – вторичной цепи.
Представление топологических уравнений.Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели различаются ориентацией на те или иные численные методы решения и набором базисных, переменных, т.е. фазовых переменных, остающихся в уравнениях итоговой ММС. Общим для всех методов является исходная совокупность топологических и компонентных уравнений (3.1)-(3.2).
При записи топологических уравнений удобно использовать промежуточную графическую форму – представление модели в виде эквивалентной схемы, состоящей из двухполюсных элементов. Общность подхода при этом сохраняется, так как любой многополюсный компонент можно заменить подсхемой из двухполюсников. В свою очередь эквивалентную схему можно рассматривать как направленный граф, дуги которого соответствуют ветвям схемы. Направления потоков в ветвях выбираются произвольно (если реальное направление при моделировании окажется противоположным, то это приведет лишь к отрицательным численным значениям потока).
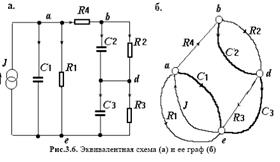
Примернекоторой простой эквивалентной схемы и соответствующего ей графа приведен на рис. 3.6. Для конкретности и простоты изложения на рис. 3.6 использованы условные обозначения, характерные для электрических эквивалентных схем, по той же причине далее в этом параграфе часто применяется электрическая терминология. Очевидно, что поясненные выше аналогии позволяют при необходимости легко перейти к обозначениям и терминам, привычным для механиков.
Для получения топологических уравнений все ветви эквивалентной схемы разделяют на подмножества хорд и ветвей дерева. Имеется в виду покрывающее (фундаментальное) дерево, т.е. подмножество из (β-1 дуг, не образующее ни одного замкнутого контура, где β – число вершин графа (узлов эквивалентной схемы). На рис. 3.6,б показан граф эквивалентной схемы рис. 3.6,а, толстыми линиями выделено одно из возможных покрывающих деревьев.
Выбор дерева однозначно определяет вектора напряжений Ux и токов Ix хорд, напряжений Uвд и токов Iвд ветвей дерева и приводит к записи топологических уравнений в виде
где М– матрица контуров и сечений, М Т – транспонированная М-матрица.
В М-матрице число строк соответствует числу хорд, число столбцов равно числу ветвей дерева. М-матрица формируется следующим образом. Поочередно к дереву подключаются хорды. Если при подключении к дереву р-й хорды q-я ветвь входит в образовавшийся контур, то элемент Mpq матрицы равен +1 при совпадении направлений ветви и подключенной хорды, Mpq= -1 при несовпадении направлений. В противном случае Mpq = 0.
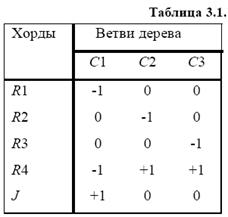
Для схемы на рис. 3.6 М-матрица представлена в виде табл. 3.1
Особенности эквивалентных схем механических объектов.Для каждой степени свободы строят свою эквивалентную схему. Каждому телу с учитываемой массой соответствует узел схемы (вершина графа). Один узел, называемый базовым, отводится телу, отождествляемому с инерциальной системой отсчета.
Каждый элемент массы изображают ветвью, соединяющей узел соответствующего массе тела с базовым узлом; каждый элемент упругости – ветвью, соединяющей узлы тел, связанных упругой связью; каждый элемент трения – ветвью, соединяющей узлы трущихся тел. Внешние воздействия моделируются источниками сил i
В качестве примера на рис. 3.7,а изображена некоторая механическая система – тележка, движущаяся по дороге и состоящая из платформы А, колес В1, В2 и рессор С1, C2. На рис. 3.7,б приведена эквивалентная схема для вертикальных составляющих сил и скоростей, на которой телам системы соответствуют одноименные узлы, учитываются массы платформы и колес, упругость рессор, трение между колесами и дорогой; неровности дороги вызывают воздействие на систему, изображенное на рис. 3.7,б источниками силы.
Характеристика методов формирования ММС.Исходную систему компонентных и топологических уравнений (3.1) и (3.2) можно рассматривать как окончательную ММС, которая и подлежит численному решению. Численное решение этой системы уравнений предполагает алгебраизацию дифференциальных уравнений, например, с помощью преобразования Лапласа или формул численного интегрирования. В программах анализа нелинейных объектов на макроуровне, как правило, применяются формулы численного интегрирования, примером которых может служить неявная формула Эйлера
где Vi— – значение переменной V на i-м шаге интегрирования; hn= tn– tn-1 – шаг интегрирования. Алгебраизация подразумевает предварительную дискретизацию независимой переменной t (вместо непрерывной переменной t получаем конечное множество значений tn), она заключается в представлении ММС в виде системы уравнений
с неизвестными Vn и Zn, где использовано обозначение Z = dV/dt. Эту систему алгебраических уравнений, в общем случае нелинейных, необходимо решать на каждом шаге численного интегрирования исходных дифференциальных уравнений.
Однако порядок этой системы довольно высок и примерно равен 2α+γ, где α – число ветвей эквивалентной схемы (каждая ветвь дает две неизвестные величины – фазовые переменные типа потока и типа потенциала, за исключением ветвей внешних источников, у каждой из которых неизвестна лишь одна фазовая переменная), γ – число элементов в векторе производных. Чтобы снизить порядок системы уравнений и тем самым повысить вычислительную эффективность ММС, желательно выполнить предварительное преобразование модели (в символическом виде) перед ее многошаговым численным решением. Предварительное преобразование сводится к исключению из системы части неизвестных и соответствующего числа уравнений. Оставшиеся неизвестные называют базисными. В зависимости от набора базисных неизвестных различают несколько методов формирования ММС.
Согласно методу переменных состояния (более полное название метода – метод переменных, характеризующих состояние), вектор базисных переменных W состоит из переменных состояния. Этот вектор включает неизбыточное множество переменных, характеризующих накопленную в системе энергию. Например, такими переменными могут быть скорости тел (кинетическая энергия определяется скоростью, так как равна Ми 2 /2), емкостные напряжения, индуктивные токи и т.п. Очевидно, что число уравнений не превышает γ. Кроме того, итоговая форма ММС оказывается приближенной к явной форме представления системы дифференциальных уравнений, т.е. к форме, в которой вектор dW/dt явно выражен через вектор W, что упрощает дальнейшее применение явных методов численного интегрирования. Метод реализуется путем особого выбора системы хорд и ветвей дерева при формировании топологических уравнений. Поскольку явные методы численного интегрирования дифференциальных уравнений не нашли широкого применения в программах анализа, то метод переменных состояния также теряет актуальность и его применение оказывается довольно редким.
В классическом варианте узлового метода в качестве базисных переменных используются узловые потенциалы (т.е. скорости тел относительно инерциальной системы отсчета, абсолютные температуры, перепады давления между моделируемой и внешней средой, электрические потенциалы относительно базового узла). Число узловых потенциалов и соответственно уравнений в ММС оказывается равным β-1, где β – число узлов в эквивалентной схеме. Обычно β заметно меньше α и, следовательно, порядок системы уравнений в ММС снижен более чем в два раза по сравнению с порядком исходной системы.
Однако классический вариант узлового метода имеет ограничения на применение и потому в современных программах анализа наибольшее распространение получил модифицированный узловой метод.
Узловой метод. Матрицу контуров и сечений М в узловом методе формируют следующим образом. Выбирают базовый узел эквивалентной схемы и каждый из остальных узлов соединяют с базовым фиктивной ветвью. Именно фиктивные ветви принимают в качестве ветвей дерева, а все реальные ветви оказываются в числе хорд. Поскольку токи фиктивных ветвей равны нулю, а вектор напряжений фиктивных ветвей есть вектор узловых потенциалов φ, то уравнения (3.13) и (3.14) принимают вид
U + Mφ = 0 (3.16)
M T I = 0 (3.17)
где U и I- векторы напряжений и токов реальных ветвей.
Компонентные уравнения алгебраизуются с помощью одной из формул численного интегрирования, линеаризуются с помощью разложения в ряд Тейлора с сохранением только линейных членов, и их представляют в виде
где Gn – диагональная матрица проводимостей, рассчитанная в точке tn; An – вектор, зависящий от значений фазовых переменных на предшествующих шагах интегрирования и потому уже известный к моменту времени tn. Каждая ветвь (за исключением идеальных источников напряжения) имеет проводимость, которая занимает одну из диагональных клеток матрицы проводимостей. Окончательно ММС получаем, подставляя (3.18) и затем (3.16) в (3.17):
M T In=M T (GnUn + An) =-M T GnMφn +M T An = 0
где Яn=М Т GnM – матрица Якоби, Вn = М Т Аn – вектор правых частей. Отметим, что матрица М имеет размер равен α×(β-1), матрица Gn –α×α, а матрица Якоби имеет размер – (β-1)×(β-1).
Система (3.19) является системой линейных алгебраических уравнений, полученной в результате дискретизации независимой переменной, алгебраизации дифференциальных уравнений и линеаризации алгебраических уравнений. Алгебраизация приводит к необходимости пошагового вычислительного процесса интегрирования, линеаризация – к выполнению итерационного вычислительного процесса на каждом шаге интегрирования.
Рассмотрим, каким образом определяются проводимости ветвей.
Для резистивных ветвей проводимость – величина, обратная сопротивлению R.
При использовании неявного метода Эйлера проводимость емкостной ветви получается из ее компонентного уравнения следующим образом.
На п-мшаге интегрирования
проводимость 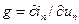
при этом в вектор правых частей входит элемент
Проводимость индуктивной ветви можно найти аналогично:
Аналогично определяют проводимости и при использовании других разностных формул численного интегрирования, общий вид которых
где μn зависит от шага интегрирования, ηn от значений вектора U на предыдущих шагах.
Классический вариант узлового метода имеет ограничения на применение. Так, недопустимы идеальные (с бесконечной проводимостью) источники напряжения, зависимые источники, аргументами которых являются токи, а также индуктивности, поскольку в классическом варианте токи не входят в число базисных переменных. Устранить эти ограничения довольно просто – нужно расширить совокупность базисных координат, включив в нее токи-аргументы зависимых источников, а также токи ветвей индуктивных и источников напряжения. Полученный вариант метода называют модифицированным узловым методом.
Согласно модифицированному узловому методу, в дерево при построении матрицы М включают ветви источников напряжения и затем фиктивные ветви. В результате матрица М принимает вид (табл. 3.2), где введены обозначения: UИCT(I) – источники напряжения, зависящие от тока; Е(t) – независимые источники напряжения; IИСТ(I) – источники тока, зависящие от тока; L – индуктивные ветви; Mij— – подматрица контуров хорд группы i и сечений фиктивных ветвей группы j.
Те же обозначения UИCT, I, E, IИСТ будем использовать и для соответствующих векторов напряжений и токов. Назовем ветви, токи которых являются аргументами в выражениях для зависимых источников, т.е. входят в вектор I, особыми ветвями. Остальные ветви (за исключением индуктивных) – неособые. Введем также обозначения: IL – вектор индуктивных токов; Ix и Ux. – векторы токов и напряжений неособых ветвей; Gx, GL, GI– диагональные матрицы проводимостей ветвей неособых, индуктивных, особых.
Уравнение закона токов Кирхгофа (3.17) для фиктивных ветвей имеет вид
Исключим вектор IХ с помощью компонентного уравнения (3.18), а вектор IИСТ с помощью очевидного уравнения
IИСТ=KI
где 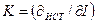
Получаем систему из трёх матричных уравнений с неизвестными векторами φ,I, IL:
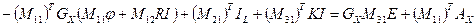
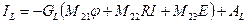

где обозначено 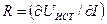
Замечания:
1. Вектор индуктивных токов нельзя исключить из итоговой системы уравнений, так как его значения входят в вектор AL на последующих шагах численного интегрирования.
2. Источники тока, зависящие от напряжений, относятся к неособым ветвям, их проводимости 
3. Источники напряжения, зависящие от напряжений, в приведенных выше выражениях не учитываются, при их наличии нужно в матрице М выделить столбец для этих ветвей, что приводит к появлению дополнительных слагаемых в правых частях уравнений (3.19) – (3.21).
Дата добавления: 2017-03-29 ; просмотров: 911 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Лекция по электротехнике 4.1 - Двухполюсник. Треугольники сопротивлений и проводимостейСкачать

Операторные компонентные уравнения и схемы замещения идеализированных пассивных двухполюсников
Сопротивление
Соотношения между мгновенными значениями тока и напряжения на зажимах сопротивления устанавливаются выражениями:
Учитывая, что умножение функции времени на постоянное число соответствует умножению изображения функции на это же число, получаем:
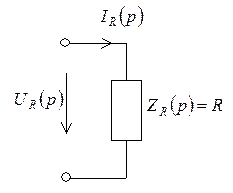 Рис. 6.17 Операторная схема замещения сопротивления Рис. 6.17 Операторная схема замещения сопротивления | 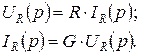 Операторное входное сопротивление и операторная входная проводимость сопротивления определяется выражениями: Операторное входное сопротивление и операторная входная проводимость сопротивления определяется выражениями: 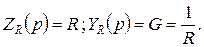 Операторная схема замещения сопротивления приведена на рис. 6.17. Операторная схема замещения сопротивления приведена на рис. 6.17. |
Емкость
Напряжение и ток емкости связаны между собой соотношениями
Используя теоремы дифференцирования и интегрирования, получаем
При нулевых начальных условиях они вырождаются в выражения
откуда находим операторное входное сопротивление и операторную входную проводимость емкости:
Операторным компонентным уравнениям при ненулевых начальных условиях соответствуют последовательная и параллельная схемы замещения емкости, содержащие независимый источник тока или напряжения (рис. 6.18 а, б). При нулевых начальных условиях независимые источники тока или напряжения, характеризующие начальный запас энергии в элементе, выключаются, и в операторной схеме замещения остается один элемент — операторное входное сопротивление или операторная входная проводимость емкости (рис. 6.18, в).
Рис. 6.18. Операторные схемы замещения емкости:
а – параллельная при ненулевых начальных условиях; б – последовательная при ненулевых начальных условиях; в – при нулевых начальных условиях
Индуктивность
Мгновенные значения тока и напряжения для индуктивности связаны между собой следующими соотношениями:
Применяя к этим выражениям теоремы дифференцирования и интегрирования, получаем компонентные уравнения индуктивности в операторной форме:
При нулевых начальных условиях эти уравнения примут вид
Используя эти выражения, определяем операторное входное сопротивление и операторную входную проводимость индуктивности:
Операторным компонентным уравнениям при ненулевых начальных условиях соответствуют последовательная и параллельная схемы замещения индуктивности, содержащие независимый источник тока или напряжения (рис. 6.19 а, б).
Рис. 6.19. Операторные схемы замещения индуктивности:
а – параллельная при ненулевых начальных условиях; б – последовательная при ненулевых начальных условиях; в – при нулевых начальных условиях
Используя операторные схемы замещения идеализированных пассивных элементов, можно получить операторную схему замещения произвольного участка линейной цепи или всей цепи в целом. С этой целью каждый идеализированный пассивный элемент должен быть заменен операторной схемой замещения, а токи и напряжения идеализированных источников тока и напряжения — представлены соответствующими операторными изображениями.
Используя операторную схему замещения цепи, можно с помощью любого из известных методов сформировать систему уравнений электрического равновесия в операторной форме, которая будет равносильна основной системе уравнений электрического равновесия цепи после коммутации.
Метод анализа переходных процессов в линейных цепях, основанный на формировании операторных уравнений электрического равновесия цепей по их операторным схемам замещения, получил название операторного метода анализа переходных процессов.
Дата добавления: 2020-10-14 ; просмотров: 335 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📹 Видео
лекция 9. Метод Активного двухполюсникаСкачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Химия | Молекулярные и ионные уравненияСкачать

ТОЭ 78. Переходные процессы в электрических цепях, составление характеристических уравнений 1 способСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Урок 455. Уравнение ШрёдингераСкачать

Урок 327. Гармонические колебанияСкачать

Урок 461. Периодическая система элементов часть 1Скачать

Химические Цепочки — Решение Цепочек Химических Превращений // Химия 8 классСкачать

БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атомаСкачать

3 14 Уравнения МаксвеллаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Симметричные электрические цепи постоянного тока | Олимпиадная физика, задачи | 9, 10, 11 класс LIVEСкачать

Лекция 020-2. Эквивалентные преобразования электрических цепейСкачать