Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как 
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида 
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи

2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
Видео:Урок 146 (осн). Изображение схем электрических цепейСкачать

Комплексная схема цепи
Покажем на примере электрической цепи синусоидального тока ее вид и математическое описание.
| Исходная схема цепи | Развернутая комплексная схема цепи | Компактная комплексная схема цепи |
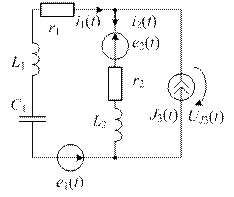 | 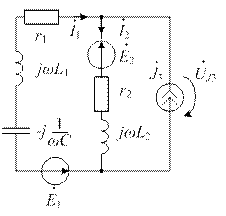 | 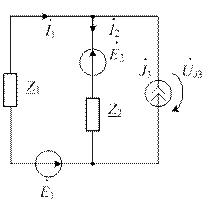 |
| e1(t), e2(t), J3(t), i1(t), i2(t), uJ3(t) — синусоидальные функции времени. | 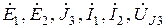 — комплексы, соответствующие функциям времени. — комплексы, соответствующие функциям времени. | 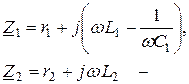 комплексные сопротивления ветвей. комплексные сопротивления ветвей. |
Описание режимов в электрических цепях по комплексным схемам замещения по законам Кирхгофа
| Для развернутой схемы цепи | 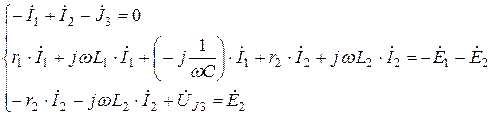 |
| Для компактной схемы цепи | 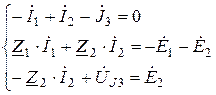 |
Если сравнить компактную схему и ее описание с подобной цепью постоянного тока, то можно сделать вывод о том, что они относятся к одному классу уравнений – это линейные алгебраические уравнения. Различие только в том, что в первой системе коэффициенты являются комплексными числами 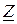
Из этого следует, что все свойства и методы расчета линейных цепей постоянного тока можно применить и к расчету цепей синусоидального тока комплексным методом.
Дата добавления: 2016-01-29 ; просмотров: 3083 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Комплексные уравнения электрического состояния цепи.
Электрическое состояние цепей синусоидального тока, так же как и цепей постоянного тока, описывается с помощью уравнений, составленных в соответствии с законами Кирхгофа.
В общем виде тригонометрическое уравнение по первому закону Кирхгофа для узла цепи синусоидального тока имеет вид

где n – число ветвей, сходящихся в узле.
Этому уравнению соответствует уравнение первого закона Кирхгофа в комплексной форме (например, для действующих значений)

Правила знаков при составлении уравнений (58) остаются теми же, что и в цепях постоянного тока: токи, положительные направления которых направлены от узла, следует брать со знаком минус, а токи, положительные направления которых направлены к узлу – со знаком плюс.
Для любого контура цепи с синусоидальными напряжениями справедливо тригонометрическое уравнение, составленное по второму закону Кирхгофа.
В идеализированных электрических цепях магнитное поле считается сосредоточенным только на участках цепи, содержащих индуктивные элементы. При обходе замкнутого контура цепи всегда можно выбрать путь, лежащий вне переменного магнитного поля, а участок, содержащий индуктивный элемент, характеризовать разностью потенциалов, т. е. напряжением на его зажимах; при этом изменение потенциала в любом замкнутом контуре цепи синусоидального тока равно нулю. Поэтому, согласно второму закону Кирхгофа, алгебраическая сумма мгновенных значений напряжений всех участков замкнутого контура равна нулю:

где m — число участков, рассматриваемого контура.
Тригонометрическое уравнение можно заменить соответствующим ему комплексным уравнением второго закона Кирхгофа (например, для действующих значений)

Применительно к схемам замещения с источниками ЭДС второй закон Кирхгофа можно сформулировать таким образом: алгебраическая сумма комплексных напряжений на пассивных элементах замкнутого контура равна алгебраической сумме сторонних ЭДС, входящих в этот контур:

Правила знаков при составлении уравнений (60) и (61) остаются теми же, что и в цепях постоянного тока: слагаемые берут со знаком плюс в случае, когда направление обхода совпадает со стрелкой положительного направления соответственно напряжения, тока или ЭДС.
Последовательное соединение элементов в цепи синусоидального тока.
Рассмотрим в качестве примера цепь с последовательным включением резистора, индуктивной катушки и конденсатора. Такая цепь с достаточной точностью описывается схемой замещения, представленной на рисунке 13. Найдем связь между напряжением на входе цепи 
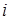
 |
Запишем уравнение по второму закону Кирхгофа в комплексной форме:

Выразим слагаемые правой части уравнения через комплексное значение тока 
и перепишем (62) в виде

Соотношение (63) является записью закона Ома рассматриваемой цепи в комплексной форме, а комплекс 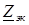

Таким образом, при последовательном соединении элементов цепи эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлений всех последовательно включенных элементов, т. е. правило определения эквивалентного комплексного сопротивления последовательной цепи совпадает с аналогичным правилом для цепи постоянного тока. Очевидно, полученный результат справедлив для цепи с последовательным включением любого числа элементов.
Пример расчёта цепи синусоидального тока.
Произведём расчёт токов цепи синусоидального тока, представленной на рисунке 14.
 |

где 
Токи в схеме рисунка 14 можно рассчитать любым методом, аналогичным образом как для цепи постоянного тока.
Метод контурных токов.
В схеме рисунка 14 задаём направление неизвестных токов. Также выбираем направление контурных токов (например, по часовой стрелке). В схеме рисунка 14 можно выделить три контурных тока. Последовательные соединения 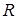


 |
Для схемы рисунка 15 получаем эквивалентные сопротивления

источники ЭДС в комплексной форме
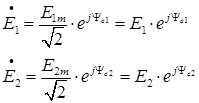
Для определения контурных токов необходимо составить следующую систему уравнений:

Уравнения для контурных токов можно записать в матричной форме:

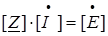
Решением уравнения (70) будет

Далее необходимо определить неизвестные токи через контурные токи:

Метод узловых потенциалов.
Аналогичным образом, как в методе контурных токов, представляем исходную схему в виде, представленном на рисунке 16.
 |
В схеме (рисунок 16) потенциал 

Уравнения для узловых потенциалов (73) можно записать в матричной форме:


где 


Решением уравнения (75) будет

Далее определяются токи

Баланс мощности.
Потребляемая полная мощность:

где 

Полная мощность источников:

где 

Потенциальная диаграмма.
Построим потенциальную диаграмму для левого контура, представленного на рисунке 17, исходной схемы (рисунок 14).
 |
На данном примере (рисунок 17) получаем

Если потенциалы (80) перенести на комплексную плоскость, то должна получиться замкнутая траектория. При этом, потенциал 
💡 Видео
Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Расчет символическим методом однофазных цепей переменного токаСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

ОТЦ 2021. Лекция 11. Комплексное сопротивление простых RC и RL цепей.Скачать
Расчет цепей переменного синусоидального тока | Метод комплексных амплитуд | Часть 3Скачать

1 3 4 Комплексные схемы замещения идеализированных пассивных элементовСкачать

Математика это не ИсламСкачать

Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

2 2 Элементы схем замещенияСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Основы электротехники. 02. Электрическая цепьСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

1 3 5 Анализ простейших линейных цепейСкачать

Построение матриц электрических цепейСкачать
















































