- Просмотр содержимого документа «Тесты по теме: «Комплексные числа»»
- Урок-семинар «Комплексные числа»
- ПЛАН УРОКА
- 1. Историческая справка
- 2. Работа по группам
- 3. Выступление учащихся с задачами повышенной сложности (3 чел.)
- 4. Работа по группам
- Ход урока
- 1. Историческая справка
- Проверочная работа по теме : «Комплексные числа»
- Содержимое разработки
- 📸 Видео
Просмотр содержимого документа
«Тесты по теме: «Комплексные числа»»
Тест «Комплексные числа»
Часть I. Выберите один правильный ответ.
1. На множестве действительных чисел не выполнима операция:
а) деления чисел
б) возведения в степень отрицательного числа
в) извлечения арифметического корня из отрицательного числа
г) сравнения чисел
2. Комплексные числа были введены для получения дополнительных возможностей при решении:
а) систем линейных уравнений
б) квадратных уравнений
в) уравнений высших степеней
г) тригонометрических уравнений
3. Что представляет собой число i:
а) число, квадратный корень из которого равен – 1
б) число, квадрат которого равен – 1
в) число, квадратный корень из которого равен 1
г) число, квадрат которого равен 1
а) действительных чисел
в) иррациональных чисел
г) комплексных чисел
5. Термин «мнимые числа» ввел:
6. Из предложенных чисел выберите чисто мнимое число:
а) вещественной частью комплексного числа
б) мнимой частью комплексного числа
в) тригонометрической формой комплексного числа
г) алгебраической формой комплексного числа
10. На координатной плоскости число изображается:
а) точкой или радиус-вектором
в) плоской геометрической фигурой
г) заштрихованной частью плоскости
11. Модулем комплексного числа называется:
а) данное комплексное число без учета знака
б) расстояние от начала координат до точки, в виде которой отображается комплексное число
в) расстояние от осей координат до точки, в виде которой отображается комплексное число
г) сумма вещественной и мнимой части
12. Модуль комплексного числа z= 4 + 3i равен:
Видео:Комплексные числа в ЕГЭ! Это просто!😱 С самого нуля до решения задачи из проекта ЕГЭ-2022 года!Скачать

Урок-семинар «Комплексные числа»
Разделы: Математика
Тема “комплексные числа” традиционно считается сложной для изучения. Завершая проходящую через весь школьный курс линию последовательного расширения числовых множеств, она связана и с другим не менее важным разделом – решение уравнений – и вместе с тем даёт возможность установления теснейших связей с геометрией. Богатое идейное и логическое содержание этой темы реализуется в задачах сравнительно высокого технического уровня.
Урок-семинар является последним завершающим в изучении темы “комплексные числа”.
Цели урока
- Применение знаний, полученных в ходе изучения темы “Комплексные числа” при решении нестандартных задач.
- Развитие познавательного интереса через привлечение исторического материала и прикладных задач.
- Систематизация знаний, умений и навыков учащихся по теме “Комплексные числа” через разбор различных методов задач.
- Активизация мыслительной деятельности учащихся.
Видео:Комплексные числа в уравненияхСкачать

ПЛАН УРОКА
1. Историческая справка
2. Работа по группам
Формируются несколько групп по 3-4 человека в каждой. Им задаются задания, подобранные таким образом, чтобы привлекался материал из различных разделов математики: условие равноудалённости точки от любых точек плоскости, определение модуля комплексного числа, уравнение окружности (задача №1); использование теоремы Виета для многочлена второй степени, изображение комплексных чисел на комплексной плоскости (задача №2); задание с параметром и определение аргумента комплексного числа (задача №3); использование формулы Муавра для возведения комплексного числа в n-ю степень (задача №4).
3. Выступление учащихся с задачами повышенной сложности (3 чел.)
Задачи предложены из экзаменационных работ.
4. Работа по группам
В каждой группе по 2 учащихся.
Для учащихся предоставляются семь задач. Цель которых одна — изобразить на комплексной плоскости все такие числа z, которые удовлетворяют различным заданным условиям. Здесь учащиеся должны упростить заданное выражение, получить либо уравнение, либо неравенство. Затем построить графики и найти нужный на доске. В это время на доске находятся все графики. Все графики различны. Они такие как: парабола, окружность, гипербола, круг, прямая , часть “кольца” и полуплоскость. Каждой задаче соответствует буква. В результате учащиеся должны получить определённое слово. (Это слово – отлично).
- Учителем приводится задача по физике, в которой можно использовать теорию комплексных чисел.
- В конце семинара проводится самостоятельная работа.
Самостоятельная работа состоит из шести задач. Эти задачи составлены по возрастанию степени сложности. Ученикам необходимо набрать нужное количество баллов, чтобы получить “5”, “4” или “3”. - Подводится итог урока, сообщаются оценки учащимся.
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Ход урока
1. Историческая справка
Если говорить об эволюции понятия числа, надо сказать, что не всегда первым толчком к расширению понятия числа были непосредственно практические потребности людей, в узком смысле этого слова. Комплексные числа, как и отрицательные, возникли из внутреннего развития математической науки, из практики решения алгебраических уравнений.
Уже в VII в.н.э. было установлено, что квадратный корень из положительного числа имеет два значения – положительное и отрицательное, а из отрицательных чисел квадратные корни извлечь нельзя: нет такого числа х, чтобы х 2 = -9.
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Первым учёным, предложившим ввести числа новой природы, был Джорж Кордано. Он предложил 

И всё-таки пришлось допустить такие корни в науку, когда другой итальянский учёный Бомбелли в 1572 году выпустил книгу, в которой были установлены первые правила арифметических операций над комплексными числами, вплоть до извлечения из них кубических корней.
Название “мнимые числа” ввёл в 1637году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare (мнимый) для обозначения числа 
В течение XVIII века продолжалось осуждение арифметической природы мнимостей, возможности дать им геометрическое истолкование.
Постепенно развилась техника операций над комплексными числами. На рубеже XVII-XVIIIв.в. была построена общая теория корней n-й степени сначала из отрицательных, а потом из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра: 

В конце XVIII-начале XIX в.было получено геометрическое истолкование комплексных чисел. Датчанин Вессель, француз Арган и немец Гаусс независимо друг от друга предложили изображать комплексное число 

В настоящее время комплексные числа используются в математике гораздо шире, чем действительные. С помощью комплексных чисел исследуется течение воды, полёт ракет и самолётов. Они применяются при вычерчивании географических карт, и многих других науках.
Работа по группам.
I. Множество Е состоит из всех комплексных чисел z, таких, что, 
9х 2 +9у 2 = (х+4) 2 + (у-8) 2
9х 2 – х 2 – 8х – 16 + 9у 2 – у 2 + 16у – 64 =0
8х 2 – 8х – 16 + 8у 2 + 16у – 64 =0
х 2 – х – 2 + у 2 + 2у – 8 =0
(х – 0,5) 2 + (у + 1) 2 = 11,25
Окружность с центром (0,5; -1)
II. Пусть Р(z) – многочлен второй степени. Известно, что его корнями являются числа -1 и i, а Р(0) = 2. Изобразите на комплексной плоскости множество всех комплексных чисел, таких, что P(z) – действительное число.
Решение.
Заменим многочлен второй степени в общем виде на b.
Т.к -1 и i – корни, то по теореме Виета
P(z) = a(z 2 + (1-i)z – i)


P(z)= P(x + yi)= 2i(x + yi) 2 + (2i + 2)(x + yi) + 2=
= 2i(x 2 +2xyi + y 2 i 2 ) + 2xi + 2x + 2yi 2 + 2yi + 2=
= 2x 2 i + 4xyi 2 – 2y 2 i + 2xy + 4x + 2yi 2 + 4yi +2=
= (– 4xy + 2x + 2 – 2y) + (2x 2 – 2y 2 + 2x + 2y)i
Т.к. по условию P(x + yi) – действительное число, то
x 2 – y 2 + x + y = 0
(x – y)(x + y) + (x + y) = 0

III. Среди всех комплексных чисел z, таких, что 

Т.к. аргумент равен 
(2 – x) 2 + (x – 3) 2 = a 2
4 – 4x + x 2 + x 2 – 6x + 9 = a 2
2(x – 2,5) 2 – 12,5 + 13 = а 2
2(x – 2,5) 2 = а 2 – 0,5
(x – 2,5) 2 = 0,5(а 2 – 0,5)
По условию ровно одно число удовлетворяет этому соотношению. Значит, уравнение должно иметь кратный корень, что возможно только лишь при 
Ответ: z = – 2,5 + 2,5i
IV. Пусть 
Ответ:
Изобразить на комплексной плоскости чисел z, удовлетворяющие условиям и получить слово.
Решение.

Пусть М – совокупность всех точек комплексной плоскости, таких что (ReU) 2 + (ZnU) 2 = 1. изобразить на чертеже множество всех точек вида: U = Z + i + 1
Решение.
Z= x + yi : U=x + yi + 1=(x + 1) + (y + 1)i
(x + 1) 2 + (y + 1) 2 = 1

Решение.
Круг с центром (0;2) R=1

Найти равнодействующую двух сил в 30 Н и 40 Н, действующих на точку тела под углом 30 0 друг другу.
Решение
Будем считать, что точка приложения сил совпадает с началом координат, а сила 



Найдите
Ответ:
2. При каких 


z = y – 3 + x 2 i – 2i = (y – 3) + (x 2 – 2)
Для того, чтобы числа были равными необходимо решить систему:
3. Представить число в тригонометрической форме
а) 
б) 
4. Составить уравнение наименьшей степени с действительными коэффициентами, имеющие корни х1= – 1; х2= 3+4i (5 б).
(x+1)(x – 3 – 4i)(x – 3+4i) = 0
Ответ: х 3 – 5х 2 + 19х + 25 = 0
5. Решить уравнение на множестве комплексных чисел 10х 4 + 39х 3 + 49х 2 + 39х + 10 = 0 (6 б).
1) 
Ответ:
6. Найти все действительные значения а, при которых уравнение имеет только комплексные корни
(a – 3)z 4 – 2(3a – 4)z 2 + 7a + 6 = 0 (10 б)
Получим уравнение (a – 3)t 2 – 2(3a – 4)t + 7a + 6 = 0
Таким образом, это уравнение имеет два действительных корня t1, t2. Для того, чтобы у исходного уравнения корни были комплексными, необходимо, чтобы t1, t2 были отрицательными.
По теореме Виета, если t1 и t2 – отрицательные, то
Ответ: решений нет.
Ученик, который набрал 16 баллов – “5”
(15 – 13) баллов – “4”
(12 – 10) баллов – “3”
Те задачи, которые ученики не успеют решить в классе, задаются на дом.
Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Проверочная работа по теме : «Комплексные числа»
Работа содержит проверочный тест для студентов 2 курса колледжа.
Содержимое разработки
Проверочная работа по теме : «Комплексные числа»
Тригонометрической формой комплексного числа называется запись вида:
а ) z = (cos f + sin f );
б ) z = r (i cos f + i sin f );
в ) z = r (cos f + i sin f).
Любое комплексное число геометрически может быть представлено в виде:
а) прямой на плоскости ;
б) точки на плоскости;
в) графика функции.
Мнимую единицу обозначают:
а) z 2 ; б) i 2 ; в) y 2
Показательной формой комплексного числа называется запись вида:
а) z = r e i ; б) z = r e i ϕ ;в) z = r e ϕ
Какое действие над комплексными числами характеризует данная формула:
а) умножение; б) деление; в) сложение; г) вычитание.
Построить на комплексной плоскости следующие комплексные числа:
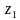
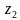
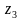
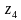
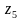
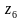
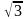
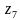
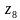
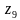
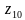
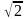
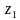
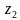
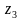
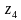
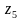
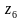
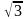
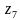
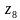
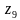
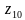
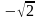
Комплексные числа заданы точками на плоскости. Тогда комплексно-сопряженными числами являются… а) А и D ; б) А и В ; в) А и С ; г) D и С .
📸 Видео
Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Комплексные числа. 11 класс.Скачать

Комплексные корни квадратных уравнений. 11 класс.Скачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

9.02.2021 17:00 «Комплексные числа помогают математике». (8-11 класс)Скачать

Тригонометрическая форма комплексного числаСкачать

Комплексные числа | Решение задачСкачать

Комплексные числа: начало. Высшая математика или школа?Скачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Тригонометрическая и показательная форма комплексного числа: Действия и Бонус | Высшая математикаСкачать

Математика без Ху!ни. Комплексные числа, часть 2. Простейшие действия.Скачать

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Высшая математика. Комплексные числа: продолжение. Возведение в степень и извлечение корняСкачать

Изобразить область на комплексной плоскостиСкачать

Найти модуль и аргумент комплексного числа #maths #complexnumbers #complexanalysis #тфкп #calculusСкачать











































