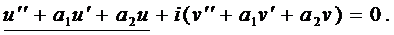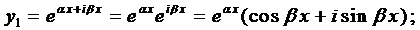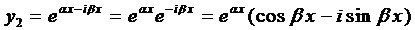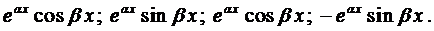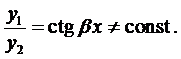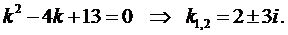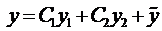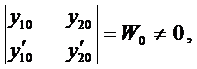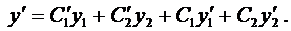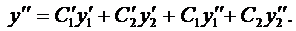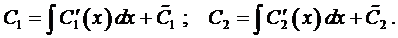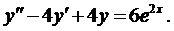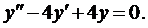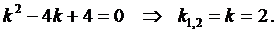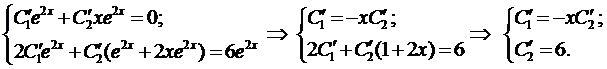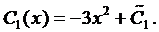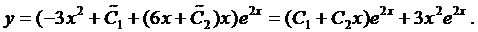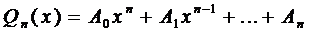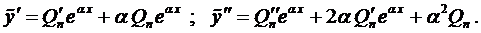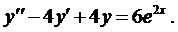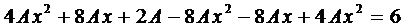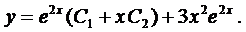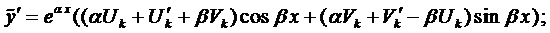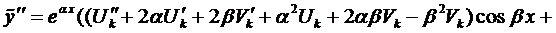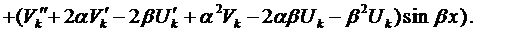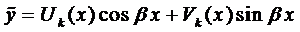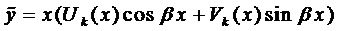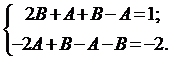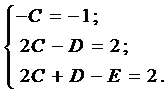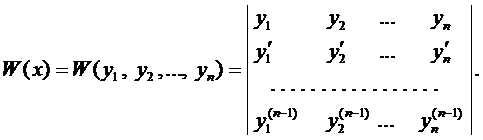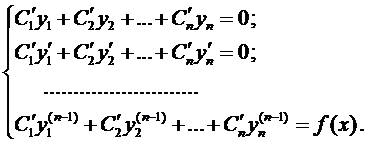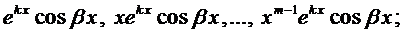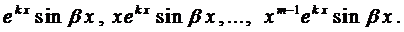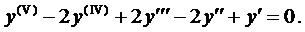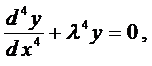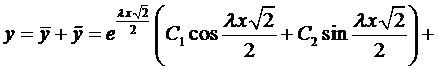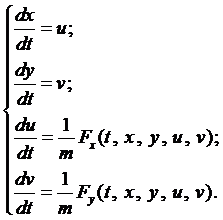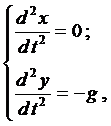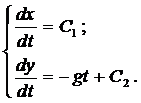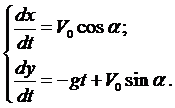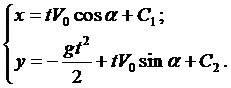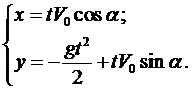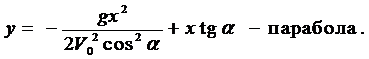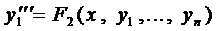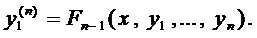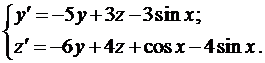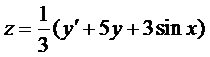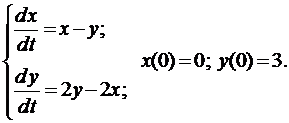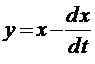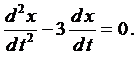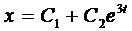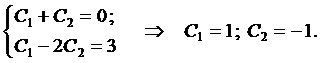Вначале покажем, что если 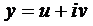
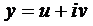
Подчеркнутый член и выражение в скобках равны нулю.
Итак, в этом случае частные решения имеют вид
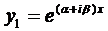
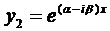
Если воспользоваться формулой Эйлера, которая будет доказана позже,

и, как показано выше, решениями уравнения (1) будут являться функции:
Очевидно, линейно-независимыми среди них будут
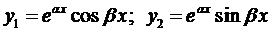
Так как
Окончательно, общее решение будет иметь вид

Пример 3. Найти общее решение уравнения 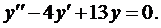
Составим характеристическое уравнение:
Воспользуемся формулой (5):
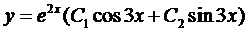
4.4. Линейные неоднородные дифференциальные уравнения второго порядка
Общий вид линейного неоднородного дифференциального уравнения второго порядка (ЛНДУ-2)
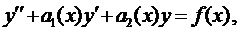
где функции 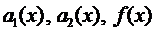
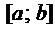
Ему соответствует однородное уравнение
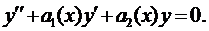
Пусть известно общее решение уравнения (7)
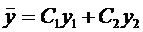
Теорема (о структуре общего решения ЛНДУ-2). Общее решение ЛНДУ-2 является суммой частного решения 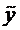
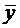
Вначале покажем, что 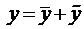
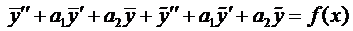
Сумма первых трёх членов левой части равенства равна нулю, так как 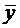
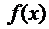
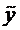
Таким образом, 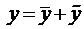
Теперь покажем, что для любых начальных условий вида 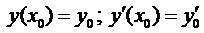
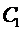
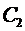
в эти условия, тогда получим систему
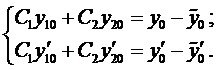
Система (9) является линейной системой для определения 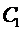
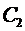
так как 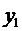
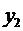
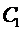
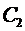
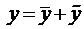
Замечание. Если 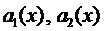
4.5. Метод вариации произвольных постоянных (метод Лагранжа)
Пусть нам известно общее решение уравнения (7), т.е. 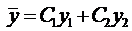
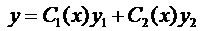
Продифференцируем это равенство:
В силу произвольности выбора функций 
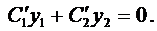
Подставляя 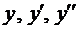
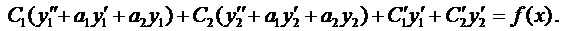
Выражения в скобках в формуле (11) равны нулю, объединяя полученные результаты, приходим к системе
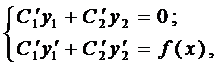
из которой единственным образом находятся 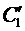
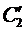
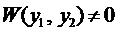
Пример 4. Методом вариации произвольных постоянных найти общее решение уравнения
Найдём общее решение соответствующего однородного уравнения
Составим характеристическое уравнение
Воспользуемся формулой (4) 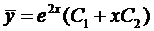
Здесь 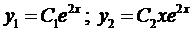
Составим систему (12)
Интегрируя последнее уравнение системы, находим 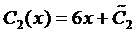
Окончательно получим общее решение
4.6. ЛНДУ-2 с постоянными коэффициентами со специальной правой частью
Общий вид линейного неоднородного дифференциального уравнения
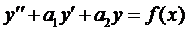
где 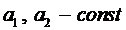
Как известно, общее решение уравнения (1) имеет вид 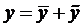

1. 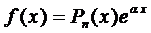
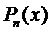
Зададим вид частного решения в форме 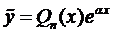
многочлен п-ой степени с неопределёнными коэффициентами. Найдём его производные:
Подставим эти выражения в уравнение (1) и сократим на
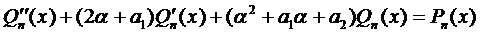
Здесь возможны случаи:
1.1. Число 
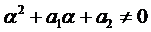
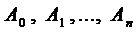
1.2. Число 
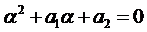
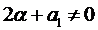
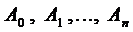
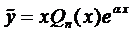
1.3. Число 
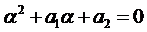
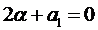
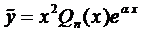
Рассмотренные три случая можно объединить общим правилом
Правило 1 . Если правая часть уравнения (1) имеет вид 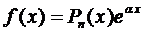
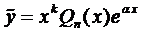
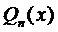
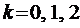

Пример 1. Найти общее решение уравнения
На предыдущей лекции было найдено общее решение соответствующего однородного уравнения

Частное решение будем искать в виде 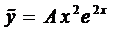
Подставим это выражение в наше уравнение и сократим на 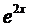
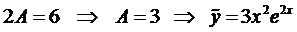
Тогда общее решение будет иметь вид
2. 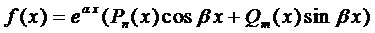
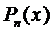
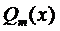
Частное решение будем искать в виде
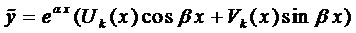
где 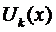
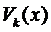
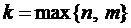
Если подставить эти выражения в уравнение (1), сократить на 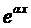
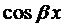
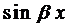
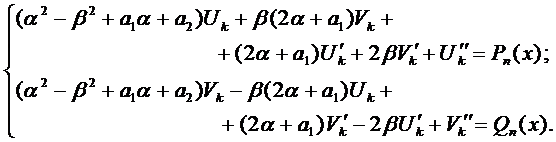
Если подставить числа 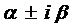
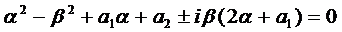
2.1. Числа 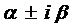
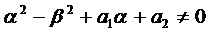
Тогда слева в уравнениях (3) стоят многочлены степени 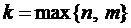
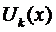
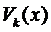
2.2. Числа 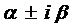
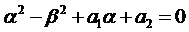
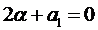
Тогда слева в уравнениях (3) стоят многочлены степени на единицу меньшую, чем k и, рассуждая аналогично, как и ранее, частное решение ищем в виде
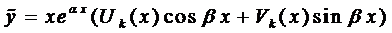
Правило 2. Если правая часть уравнения (1) имеет вид
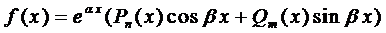
то частное решение следует искать в виде
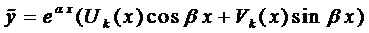
если 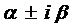
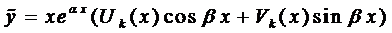
если 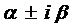
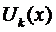
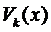
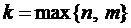
Замечание 1. Правило 2 справедливо и для случая 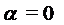
и, если 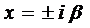
Замечание 2. Если правая часть уравнения (1) представляет собой сумму двух функций, относящихся к правилам 1-2, то частное решение в силу линейности уравнения ищется в виде суммы двух функций, которые определяются соответственно правилами 1-2.
Пример 2. Найти частное решение уравнения
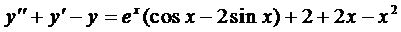
Здесь правая часть уравнения представляется в виде суммы двух функций:
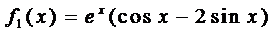
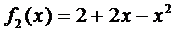
Поэтому решение ищем в виде 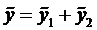
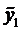
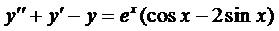
а 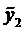
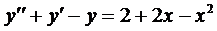
Для этого случая решение имеет вид (случай 2.1)
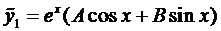
Подставим это выражение в уравнение (4):
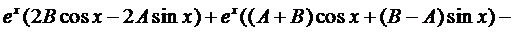
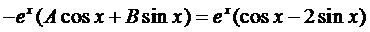
Сократим на 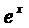
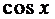
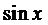
Из решения системы получаем
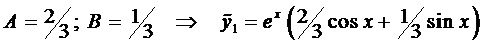
Решение уравнения (5) ищем в виде (случай 1.1)
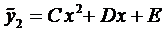
Подставим это выражение в уравнение (5)
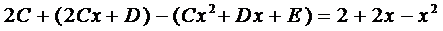
Приравнивая коэффициенты при 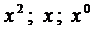
Из решения системы последовательно находим
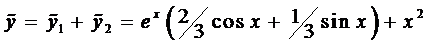
Лекция № 43. Тема 5 : Линейные ДУ высших порядков
5.1. Линейные дифференциальные уравнения п-го порядка
Общий вид линейного дифференциального уравнения п-го порядка (ЛДУ — п)
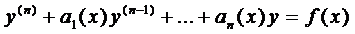
Ему соответствует однородное уравнение п-го порядка
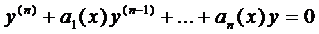
Определение 1. Функции 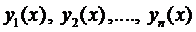
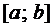
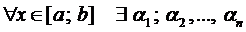
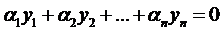
Для выяснения ЛЗ или ЛНЗ решений уравнения (2) также используется определитель Вронского, который для данного случая имеет вид
При этом, если 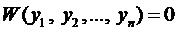
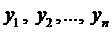
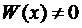
Справедливы также теоремы о структуре решений уравнений (1-2):
Теорема 1. Если 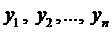
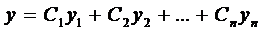
где 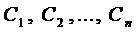
Теорема 2. Общее решение ЛНДУ — п есть сумма частного решения 
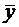
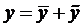
Доказательства этих теорем аналогичны, как и для случая ЛДУ – 2.
Если известно общее решение соответствующего однородного уравнения (2), то общее решение уравнения (1) можно находить методом вариации произвольных постоянных. Тогда система для нахождения функций 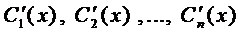
Остановимся на случае, когда все коэффициенты 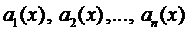
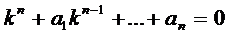
По характеру корней уравнения (3) определяются частные ЛНЗ решения:
Правило. Каждому действительному корню k характеристического уравнения (3) т-ой кратности соответствует т ЛНЗ решений вида
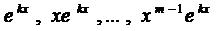
Каждой паре комплексных корней 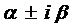
Для случая уравнения со специальной правой частью 

Пример 1. Найти общее решение ДУ
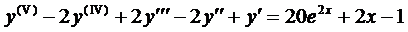
Ему соответствует однородное уравнение
Составим характеристическое уравнение
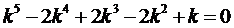
Найдём его корни
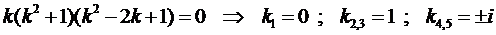
Тогда, согласно правилу, получаем общее решение однородного уравнения
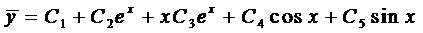
Частное решение неоднородного уравнения будем искать в виде 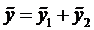
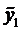
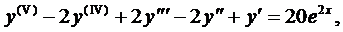
а 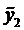
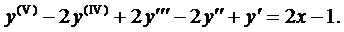
Так как число 2 не является корнем характеристического уравнения, то 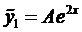
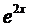
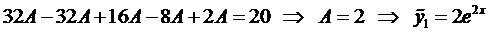
Частное решение уравнения (5) ищем в виде
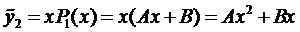
так как нуль является корнем характеристического уравнения.
Подставим это выражение в уравнение (5):
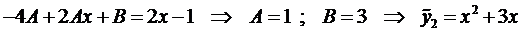
Таким образом, получаем общее решение данного уравнения
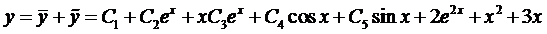
5.2*. Понятие о краевой задаче
При решении некоторых задач требуется проинтегрировать ДУ не при начальных условиях (задача Коши), а с учётом значений искомой функции или её производных в некоторых точках. Условия, налагаемые на значения функции, её производных на концах отрезка, называются краевыми условиями, а соответствующая задача – краевой задачей.
При этом для корректности решаемой задачи число таких условий должно быть равно числу констант в общем решении. Такие задачи рассматриваются в курсе сопротивления материалов, а ещё более общие задачи встречаются в курсе уравнений математической физики.
Рассмотрим в качестве примера задачу изгиба балки на упругом основании.
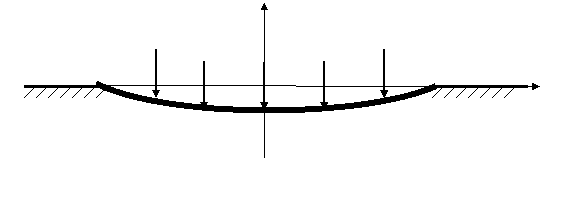
Дифференциальное уравнение прогиба балки имеет вид
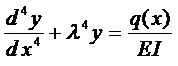
где l упругая постоянная, характеризующая свойства основания, Е — модуль упругости балки, I — момент инерции площади поперечного сечения балки, q(x) — интенсивность внешней нагрузки.
Этому уравнению соответствует однородное уравнение
для которого характеристическое уравнение имеет вид
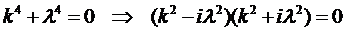
Непосредственно легко проверить, что его корнями являются
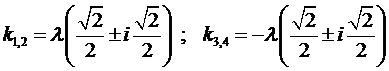
Этим корням соответствует общее решение
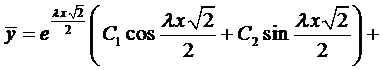
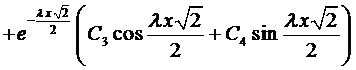
Рассмотрим случай, когда 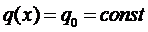
Тогда частное решение будем искать в виде 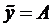
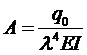
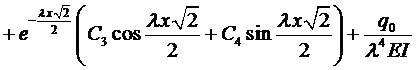
Константы 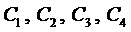
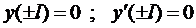
Подставляя в эти граничные условия полученное выражение для прогиба (6), получим систему четырёх уравнений для определения 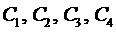
Лекция № 44. Тема 6 : Системы дифференциальных уравнений
6.1. Нормальные системы дифференциальных уравнений
К решению систем дифференциальных уравнений приводят, в частности, задачи по исследованию колебательных процессов в технике, физике, меха-нике. Вибрации сооружений, электромагнитные колебания, колебания упру-гих тел — все эти процессы описываются системами дифференциальных уравнений.
В качестве примера рассмотрим движение материальной точки массой т в плоскости Оху. Согласно второму закону Ньютона имеем
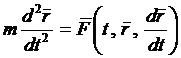
Спроектируем векторное равенство на координатные оси
Получена система дифференциальных уравнений относительно двух неизвестных функций 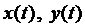
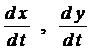
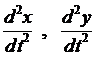
Будем рассматривать системы дифференциальных уравнений, каждое уравнение которой разрешено относительно старшей производной – канонические системы. Такую систему, путём введения дополнительных функций, всегда можно привести к эквивалентной ей системе дифференциальных уравнений первой порядка (ДУ-1), разрешенных относительно производной.
Например, приведём систему (1) к системе ДУ-1.
Введём функции 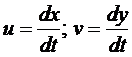
Поэтому в дальнейшем будем рассматривать только такие системы.
Определение 1. Нормальной системой дифференциальных уравнений называется система дифференциальных уравнений вида
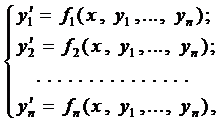
где 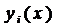
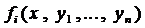
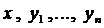
Определение 2. Решением системы (2) называется совокупность п дифференцируемых функций: 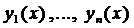
Определение 3. Совокупность функций 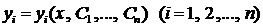
1. Эти функции являются решением системы при любых значениях 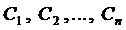
2. Для любых начальных условий вида
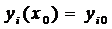
из области G можно найти такие значения 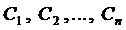
Задача Коши для системы (2) формулируется следующим образом: Найти такое решение 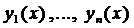
Теорема (о существовании и единственности решения задачи Коши).
Если правые части системы ДУ (2) и их частные производные по переменным 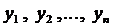
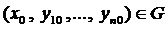
Пример 1*. Определить траекторию полёта снаряда, выпущенного из орудия под углом a к горизонту со скоростью V0. Сопротивлением воздуха пренебречь.
Вначале лекции были рассмотрены общие уравнения (1), которые можно применить для данной задачи
где g — ускорение свободного падения. Проинтегрируем каждое уравне-ние системы
Константы интегрирования 
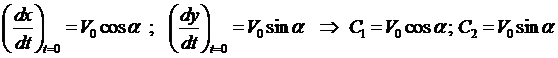
Тогда система примет вид
Ещё раз проинтегрируем
Константы интегрирования 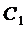
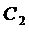
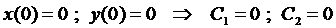
Таким образом, решением системы являются функции
Исключая параметр t, приходим к уравнению траектории
6.2. Решение нормальных систем ДУ методом исключений
Решение системы (2) сводится к решению ДУ-п методом исключений.
Продифференцируем по х первое уравнение системы (2)
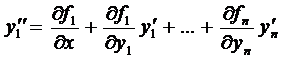
С учетом остальных уравнений системы это выражение примет вид
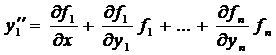
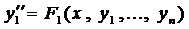
Аналогично, ещё раз продифференцировав, получаем
и т. д., пока не найдём п-ую производную
Таким образом, получаем систему п уравнений
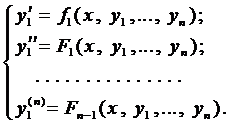
Из первых п — 1 уравнений системы (4) выразим 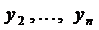
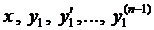
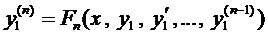
Решая уравнение (5), находим 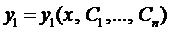
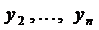
Замечание 1. Из приведённых выше рассуждений видна структура общего решения системы дифференциальных уравнений (2).
Замечание 2. Часто систему уравнений можно сразу сводить к уравнению (5), минуя систему (4). В частности, это относится к линейным системам дифференциальных уравнений.
Пример 2. Найти общее решение системы
Из первого уравнения найдем
и подставим во второе уравнение
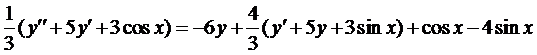
Умножим на 3 и приведём подобные члены

Составим характеристическое уравнение
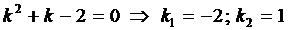
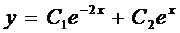
Тогда, с учетом выражения для z, получаем
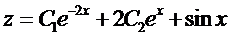
Пример 3. Решить задачу Коши
Из первого уравнения находим
и подставляем во второе уравнение
Составим характеристическое уравнение
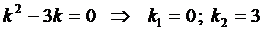
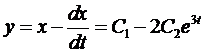
Из начальных условий получаем систему для нахождения 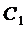
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Комплексно сопряженные корни уравнения второго порядка
3.3 Переходные процессы в цепях второго порядка
Цепи второго порядка содержат два реактивных элемента; это могут быть две индуктивности, две емкости или емкость с индуктивностью. Кроме того, цепь включает некоторое количество резистивных элементов и независимых источников энергии, которые для простоты анализа будем считать стационарными. В зависимости от наличия тех или иных реактивных элементов, решение задачи следует искать или для переменной состояния i L ( t) , или для u C ( t). Форма записи решения определена общей теорией:
где p1 и p2 — корни характеристического уравнения.
Поиск решения выполняется в той же последовательности, что и для цепей первого порядка:
1. Находят корни характеристического уравнения. Они могут быть вещественными разными и отрицательными или вещественными кратными и отрицательными или комплексно-сопряженными с отрицательной вещественной частью;
2. Из анализа цепи после коммутации определяют принужденную составляющую режима 

3. Исследуя основные и неосновные начальные условия, находят постоянные интегрирования 



Рассмотрим подробнее каждый шаг решения.
1. Определение корней характеристического уравнения.
Характеристическое уравнение может быть получено классическим методом путем составления системы уравнений по законам Кирхгофа с последующим сведением этой системы к одному дифференциальному уравнению второго порядка. Этот способ подробно описан в учебной литературе и здесь не рассматривается. Как показывают примеры, рассмотренные ранее, этот путь сопровождается достаточно громоздкими преобразованиями.
Было замечено, что характеристическое уравнение содержится внутри
функции входного сопротивления как некоторый инвариант, присущий данной цепи. Рассмотрим этот способ получения характеристического уравнения путем исследования входного сопротивления на примере цепи, представленной на рис.3.13а. Будем считать, что цепь питается от источника постоянного тока и содержит два резистивных сопротивления, индуктивность и емкость. После коммутации ( t>0) (ключ S замыкается) переходный процесс в цепи, изображенной на рис.3.13б, развивается за счет независимого источника тока, а также за счет энергии, запасенной в реактивных элементах цепи. Свободная составляющая режима, определяемая корнями характеристического уравнения, не зависит от внешнего источника питания, а определяется только параметрами элементов ветвей и способом их соединения. Точно так же не зависит от внешних источников питания и функция входного сопротивления [1]. Поэтому возникает идея поискать корни характеристического уравнения внутри функции входного сопротивления.
На рис.3.13в и рис.3.13г представлены комплексные схемы замещения цепи, которые следует составить для определения входного сопротивления со стороны
первой и третьей ветви, где 
Рис. 3.13. Схема RLC -цепи второго порядка:
а) исходная цепь
б) схема после коммутации
в) входное сопротивление со стороны третьей ветви
г) входное сопротивление со стороны первой ветви
Объединяя параллельно и последовательно соединенные ветви, найдем входные сопротивления со стороны обозначенных зажимов
Числители полученных выражений совпадают, а знаменатели различны. Аналогичный результат получим, если найдем входное сопротивление со стороны второй ветви. Следовательно, числитель входного сопротивления со стороны любой ветви является некоторым расчетным инвариантом, определяемым топологией цепи. Числитель этого инварианта при замене комплексной переменной jω на p совпадает с характеристическим полиномом. Используя эту замену и, приравнивая числитель к нулю, получим характеристическое уравнение:
После замены в числителе переменной jω на p и деления на коэффициент при старшем члене получим уравнение второй степенин.Найдем корни этого уравнения
На основании этого анализа сформулируем порядок получения характеристического уравнения цепи:
а. Для времени t>0 следует изобразить комплексную расчетную цепь;
б. Исключить из схемы все независимые источники энергии: источники тока разомкнуть, источники напряжения замкнуть накоротко. Найти входное сопротивление со стороны любой ветви и записать это выражение в виде дробно-рациональной функции, где в числителе и в знаменателе образуются полиномы по степеням jω
в. Числитель полученного выражения, совпадающий с характеристи-ческим полиномом, приравнять к нулю, предварительно заменив переменную jω на p. Найти корни характеристического уравнения и записать решение для искомой переменной состояния в виде (3.17) или (3.18).
Рис. 3.14. Схема для определения принужденных составляющих режима
2. Определение принужденной составляющей режима при стационарном воздействии находят для момента времени t = ∞, когда переходный процесс в цепи уже закончен. Для рассматриваемого в примере режима постоянного тока исследуемая схема приведена на рис.3.14, где индуктивность заменена короткозамкнутой перемычкой, а емкость разрывом. Используя правило деления тока на части, найдем
3. Постоянные интегрирования A1 и A2 (или B1 и B2) можно найти на основании основных и неосновных начальных условий. Основные начальные условия определяются законами коммутации по схеме докоммутационного состояния цепи. Для рассматриваемого примера такая схема приведена на рис.3.15а, из анализа которой следует
что дает одно уравнение для определения постоянных интегрирования:
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Частный случай: уравнение второго порядка Пусть имеем линейное однородное дифференциальное уравнение второго порядка где р, Р2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде где тогда Подставляя эти выражения для у и ее производных в уравнение (1), получаем .
Так как , то должно выполняться равенство Следовательно, функция у = eAz будет решением уравнения (1), т. е. будет обращать его в тождество по х, если А будет удовлетворять алгебраическому уравнению Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть называется характеристическим много-членом.
Уравнение (3) есть квадратное уравнение. Обозначим его корни через А] и 1 они могут быть 1) действительными и разными; 2) комплексными; 3) действительными и равными. Рассмотрим каждый случай в отдельности. 1. Если корни Л|, Аг характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции Эти решения линейно независимы (Aj Ф А2) и, следовательно, образуют фундаментальную систему решений уравнения.
Общее решение уравнения
Общее решение уравнения имеет вид — произвольные постоянные). Пример 1. Найти общее решение уравнения М Составляем характеристическое уравнение: Оно имеет корни Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Отсюда получаем искомое общее решение 2.
Пусть корни характеристического уравнения комплексные. Так как коэффициенты р], р2 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что Частные решения дифференциального уравнения (1) можно записать в виде Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями.
С помощью формул Эйлера частные решения ij и у2 уравнения (1) можно представить в виде Воспользовавшисьтеоремой 4, получим, что частными решениями уравнения (1) будут также функции _ Эти решения линейно независимы, так как Решения образуют фундаментальную систему решений уравне-ния (1), общее решение которого в этом случае имеет вид или Пример 3.
Найти общее решение уравнения 4 Характеристическое уравнение имеет кратные корни Поэтому общее решение исходного дифференциального уравнения: Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами) Пусть — частное решение уравнения. Введем новую искомую функцию ti(x) соотношением (разрешимым относительно н(х) в тех интервалах, где yi(x) не обращается в нуль).
Из этого соотношения найдем производные от у : и подставим их в уравнение (5): Для функции и(х) получаем опять уравнение порядка п, но коэффициент при м(х) есть £(yil-Он тождественно равен нулю, так как yi (х) есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = и'(х).
Разделив, кроме того, все члены последнего уравнения на yi(x) Ф 0, приведем его к виду Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка п — . Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообше, если известно г частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г единиц. 6.2.
Физические приложения: уравнение колебаний Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t: где у — отклонение колеблющейся точки от положения равновесия, rh — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению).
Характеристическое уравнение
Характеристическое уравнение для (6) имеет корни Если трение достаточно велико, h2 > Атк, то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид Так как то из (7) заключаем, что при большом трен и и отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, Атк, то характеристическое уравнение имеет комплексно сопряженные корни Общее решение уравнения (6) в этом случае определяется формулой или Отсюда видно, что в случае малого трения происходят затухающие колебания. Пусть теперь трение отсутствует, .
В этом случае характеристическое уравнение имеет чисто мнимые корни Решение уравне- ния (6) имеет вид . в этом случае происходят незатухающие гармонические колебания с частотой ш = и произвольными амплитудой А и начальной фазой 6. Задача. При каких 1) все решения уравнения стремятся к нулю при 2) каждое решение уравнения обращается в нуль на бесконечном множестве точек х? 6.3. Общий случай: уравнение произвольного порядка Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка п (п ^ 1) с постоянными коэффициентами ) гдерьрг,,Рп — действительные числа.
Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка. Ищем решение в виде Подставляя вместо у величину еХх в уравнение (8), получаем , что приводит к характеристическому уравнению 2. Находим корни характеристического уравнения. 3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что: а) Каждому действительному однократному корню А характеристическою уравнения соответствует частное решение уравнения (8).
б) Каждой паре однократных комплексно сопряженных корней соответствуют два линейно независимых частных решения уравнения (8). в) Каждому действительному корню А кратности г соответствует г линейно независимых частных решений уравнения (8). Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г характеристического уравнения . Функцию будем рассматривать как функцию двух аргументов: ж и А.
Возможно вам будут полезны данные страницы:
Она имеет непрерывные производные по а: и по А всех порядков, причем Поэтому частные производные функции по х и по А не зависят от порядка дифференцирования (операции дифференцирования функции у по х и по А перестановочны), так что Воспользовавшись этой перестановочностью, а также тем, что Если А есть г-кратный корень характеристического уравнения то стало быть, правые части (10) и (11) тождественно по х равны нулю: Это означает, что функции являются в этом случае решениями уравнения (8).
Легко проверить, что функции линейно независимы на любом интервале (a, b) изменения х. г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней.
Поэтому каждой паре комплексно сопряженных корней p кратности l отвечает 2/х частных решений уравнения 4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея п линейно независимых частных решений 3/i(x), skfc). уп(я) уравнения (8), получаем общее решение этого уравнения, где произвольные постоянные. Прммер 4. Найти общее решение уравнения Составляем характеристическое уравнение: 2. Находим корни характеристического уравнения: 3.
По характеру корней выписываем частные линейно независимые решения дифференциального уравнения: 4. Общее решение дифференциального уравнения имеет вид Схема решения линейного дифференциального уравнения с постоянными коэффициентами Дифференциальное уравнение действительные числа). Характеристическое уравнение Корни характеристического уравнения Частные линейно независимые решения дифференциального уравнения Общее решение уравнения — произвольные постоянные). §7.
Уравнения, приводящие к уравнениям с постоянными коэффициентами Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера где pi.tp2, —tPn — постоянные числа.
Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики): Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Положим Подставляя выражения для , получим дифференциальное уравнение с постоянными коэффициентами.
Последнее интегрируется обычным приемом: составляем характеристическое уравнение находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х. Пример. Найти общее решение уравнения Замена переменной х = приводит к уравнению характеристическое уравнение которого имеет корни Общее решение преобразованного уравнения равно Учитывая, что , для общего решения исходного уравнения получаем выражение Замечание 1.
Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид Поэтому можно сразу задаться этим видом частного решения. Подставляя в уравнение (1), получим для к уравнение ) совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение уравнения (1); двукратному корню отвечают два решения уравнения (1).
Паре комплексных сопряженных корней уравнения (4) будут соответствовать два решения уравнения (I). Замечание 2. Уравнение постоянные числа) подстановкой также приводится к уравнению с постоянными коэффициентами. §8. Линейные неоднородные дифференциальные уравнения Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид Здесь заданные на некотором интервале (а, р) функции. Если ао(ж) Ф 0 на (а, то после деления на ац(х) получим уравнение.
Из теоремы 1 существования и единственности решения задачи Коши получаем: если на отрезке [а, 6] коэффициенты Рк(х) и правая часть /(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям Уравнение (2) можно записать в виде где, как и выше, Теорема 12. Если у(х) есть решение неоднородного уравнения есть решение соответствующего однородного уравнения мПо условию, В силу линейности оператора £ имеем Это означает, что функция есть решение уравнения Теорема 13.
Если у(х) есть решение уравнения есть решение уравнения та функция есть решение уравнения По условию, используя линейность оператора £, получаем Последнее означает, что функция есть решение уравнения Теорема выражает так называемый принцип суперпозиции (наложения). Теорема 14. Если уравнение где все коэффициенты и функции действительные, имеет решение то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений.
По условию имеем Отсюда получаем: Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение в области — уравнения с непрерывными на отрезке коэффициентами , и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения у(х) неоднородного уравнения, т. е. Надо доказать, что где произвольные постоянные, линейно независимые решения соответствующего однородного уравнения £[у] = 0, является общим решением неоднородного уравнения.
Будем исходить из определения общего решения и просто проверим, что семейство функций у(ж), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении. В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения.
Так как для уравнения (2) при х 6 [а, Ь] выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных С, в (4) можно удовлетворить произвольно заданным начальным условиям где хо € (а,6), т.е. можно решить любую задачу Коши. Ограничимся случаем, когда п = 3.
Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания Эта линейная по отношению к система трех уравнений с тремя неизвестными допускает единственное решение относительно з при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(x$) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке ж € (а, Ь), в частности в точке ж = жо.
| Значит, какова бы ни была тройка чисел |
уо, Уо> Уо» найдется решение С?, С?, Cj системы (6) такое, что функция будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний.
Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155 Пример 1.
Найти общее решение уравнения М Нетрудно заметить, что функция является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению , есть корни его Поэтому общее решение уравнения (*) имеет вид . Общее решение исходного неоднородного уравнения:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔍 Видео
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Комплексные корни квадратных уравнений. 11 класс.Скачать

Комплексные корни квадратного уравненияСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Биквадратное уравнение 2 Комплексные корниСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Биквадратное уравнение. Комплексные корни.Скачать

ЛОДУ 2 порядка с постоянными коэффициентами. ПримерыСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

ЛОДУ II порядка с постоянными коэффициентамиСкачать

Комплексные числа в уравненияхСкачать

Математика без Ху!ни. Комплексные числа, часть 2. Простейшие действия.Скачать