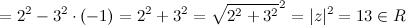Комплексно сопряженное число примеры уравнений (4 видео)

Что такое комплексно сопряженные числа

В данной публикации мы рассмотрим, что такое комплексно сопряженные числа, а также перечислим их основные свойства. Представленная теоретическая информация сопровождается практическими примерами для лучшего понимания.

Содержание

Определение комплексно сопряженных чисел
Свойства комплексно сопряженных чисел
Комплексно сопряженные числа
Свойства комплексно сопряженных чисел
Решение уравнений с комплексными числами
📽️ Видео

Видео:Сопряженные комплексные числа. ПримерСкачать

Определение комплексно сопряженных чисел

Дано комплексное число . Комплексно сопряженным к нему является число (для обозначения используется черточка сверху).

Таким образом, у комплексно сопряженных чисел действительные части одинаковые, а мнимые отличаются по знаку.

Пример:
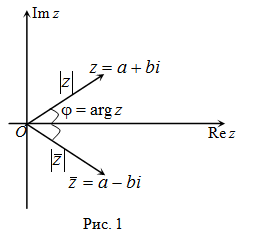
Для числа комплексно сопряженным является .

Геометрическая интерпретация

Если перенести комплексно сопряженные числа на комплексную плоскость, то они будут зеркальным отражением друг друга относительно действительной оси (RE).

Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

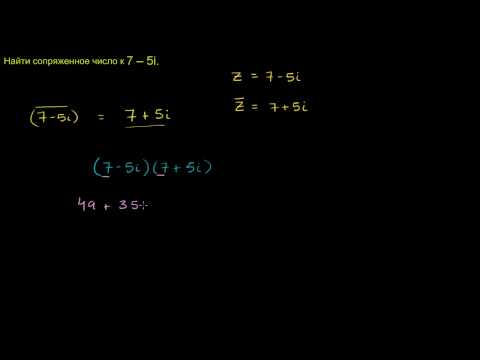
Свойства комплексно сопряженных чисел

1. Если z = z , значит число z является действительным.

Пример:
z = 2, значит , следовательно , т.е. .

2. Модули комплексно сопряженных чисел равны, т.е. . А так как такие числа на комплексной плоскости зеркальны, то их аргументы отличаются по знаку.

3. Сумма комплексно сопряженных чисел – это действительное число: .

4. Произведение комплексно сопряженных чисел равняется квадрату их модуля и является действительным числом: .

Модуль считается так:

5. Для и справедливо:

6. Для произвольных комплексных чисел z₁ и z₂ :

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Комплексно сопряженные числа

Если $z=a+b i$, то число $overline=a-b i$ называется комплексным сопряженным к числу $z$ .

То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.

Например. Комплексно сопряженным к числу $z=2-i$ есть число $overline=2+i$ .

На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.

Видео:комплЕксные ЧИСЛА решение примеров МАТЕМАТИКАСкачать

Свойства комплексно сопряженных чисел

1) Если $z=overline$, то можно сделать вывод, что рассматриваемое число $z$ является действительным.

Например. $z=2 in R Rightarrow overline=2$ и $z=overline$

2) Для любого комплексного числа $z$ сумма $z+overline=2 operatorname z$ — действительное число.

Например. Пусть $z=2-3 i$, тогда $overline=2+3 i$, а тогда

$z+overline=2-3 i+(2+3 i)=2-3 i+2+3 i=2+2=4 in R$

3) Для произвольного комплексного числа $z=a+b i$ произведение $z cdot overline=|z|^ in R$ .

Например. Пусть $z=2-3 i$, комплексно сопряженное к нему число $overline=2+3 i$, тогда произведение

4) Модули комплексно сопряженных чисел равны: $|z|=|overline|$, а аргументы отличаются знаком (рис. 1).

5) $overline <z_pm z_>=overline_ pm overline_$

6) $overline <z_cdot z_>=overline<z_> cdot overline_$

9) Если $z=a+b i$ и $overline=a-b i$ — комплексно сопряженные числа, то

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.