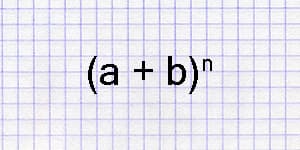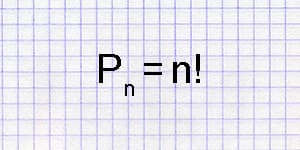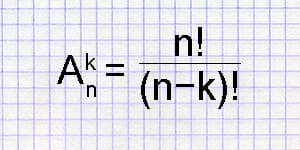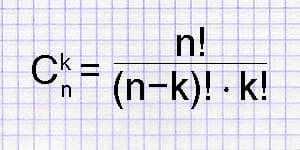Комбинаторика решить уравнение онлайн калькулятор (8 видео)

Содержание

Комбинаторика
Правила в комбинаторике
Элементы комбинаторики
Комбинаторика
Комбинаторика
Комбинаторика онлайн калькуляторы
Смотрите также
📺 Видео

Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать

Комбинаторика

Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.

Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Правила в комбинаторике

Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.

Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n₁ способом, второе n₂ и далее до n_k, то все действия этой последовательности можно выполнить n₁ · n₂ · n_k способами.

Видео:Комбинаторика. Сочетание. 10 класс.Скачать

Элементы комбинаторики

Размещения из n по k – упорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Для расчета способов размещения следует воспользоваться формулой: P k _n = n! / (n — k)!

Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: P_n = n!

Сочетания из n по k – неупорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Число сочетаний из n элементов по k рассчитывается так: n! / (n — k)! · k!

Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.

Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.

Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.

Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.

Видео:9 класс, 26 урок, Комбинаторные задачиСкачать

Комбинаторика

Комбинаторика изучает всевозможные варианты развития событий, а также рассчитывает их вероятности. Если упростить вид комбинаторики до манипуляций с множеством, количество элементов которого первоначально задано, то основными функциями комбинаторики будут перестановки (факториал), размещения и сочетания. В этом разделе Вы найдете определения всех трех понятий, а также формулы и их происхождение. Чтобы вычислить размещения, сочетания или найти факториал, Вы можете воспользоваться приведенным алгоритмом действий или ввести заданные параметры в он-лайн калькулятор комбинаторики, который сразу рассчитает необходимый результат.

Видео:Комбинаторика. Размещение. 10 класс.Скачать

Комбинаторика

Комбинаторика онлайн калькуляторы

Элементы комбинаторики перестановки, размещения, сочетания	Число перестановок находит все варианты перестановки
Обратная перестановка онлайн калькулятор	Количество инверсий в перестановке это количество пар элементов
Циклическая перестановка перевод цикла в стандарт	Число сочетаний вычисление числа сочетаний из n по k элементов
Порядок перестановки стандартной и циклической	Число сочетаний с повторениями онлайн калькулятор для нахождения сочетаний
Число размещений нахождение количества размещений	Разложение Бинома Ньютона калькулятор разложения степени
Комбинаторные уравнения решение комбинаторных уравнений

Смотрите также

Сколько существует трёхзначных чисел, которые делятся на 5?

Подскажите что использовать, перестановки с повторениями? Есть восемь элементов у каждого элемента может быть два состояния. Сколько может быть комбинаций?

составьте всевозможные перестановки из элементов множества А, если а=,иллюстрируйте решение, используя понятие регулярного дерева

У Васи есть кубики трех цветов. Он строит из них башню, ставя каждый следующий кубик на предыдущий. Запрещено использовать более 7 кубиков каждого из цветов. Вася заканчивает строить башню, как только в ней окажется по 7 кубиков каких-то двух цветов. Сколько различных башен может построить Вася?

Сколько существует четырехзначных чисел, в запись которых входит ровно одна цифра 3?

Рассмотрим четыре случая:
1) Когда число начинается на 3.
Каждый разряд (сотен, десятков и единиц) можно выбрать девятью способами.
9 × 9 × 9 = 729 чисел.

2) Когда цифра 3 в разряде сотен.
Первую цифру можем выбрать восемью способами, а третью и четвертую – девятью способами, получаем.
8 × 9 × 9 = 648 чисел.

3) Когда цифра 3 в разряде десяток.
8 × 9 × 9 = 648 чисел.

4) Когда цифра 3 в разряде единиц.
8 × 9 × 9 = 648 чисел.

Общее количество: 729 + 648 + 648 + 648 = 2673 чисел.