Количество решений системы уравнений ax b не может быть равным

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Количество решений системы уравнений ax b не может быть равным

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Видео:Количество решений системы уравнений. УпражнениеСкачать

2.1. Системы линейных уравнений и их решение методом Гаусса

Решение различного рода систем уравнений – классическая и часто возникающая (в том числе и в экономике) математическая проблема. В данном параграфе мы остановимся на простейших из систем – На системах линейных уравнений. Именно они чаще других находят применение в экономике (да и не только в ней).

Системой линейных уравнений называется система вида:

a11X1 + a12X2 +… + a1NXn = b1

В этой системе M уравнений с N неизвестными (X1; X2; …Xn). А линейными уравнения, входящие в систему (1.1), называются потому, что неизвестные (X1; X2; …Xn) этих уравнений входят в них в первой степени (линейно). То есть аналогично тому, как входят в линейную функцию величины X и Y.

Систему (1.1) можно записать и в сжатой (сокращенной) форме, используя знак суммирования å:

(I = 1, 2,… M) (1.2)

Числа Aij (I = 1, 2,… M; J = 1, 2,… N) – заданные коэффициенты при неизвестных Xj (J = 1, 2,… N); числа Bi (I = 1, 2,… M) – так называемые свободные члены системы, которые тоже заданы.

Определение. Любой набор значений неизвестных (X1; X2; …Xn), удовлетворяющих всем уравнениям системы, называется ее решением (частным решением). Система считается решенной, если найдены Все ее решения (или доказано, что никаких решений у нее нет).

В частности, если все свободные члены системы <B1; B2; …Bm> равны нулю, то система (1.1) принимает вид

a11X1 + a12X2 +… + a1NXn = 0

И называется Линейной однородной системой (а все прочие системы (1.1) являются Линейными неоднородными). Любая линейная однородная система (1.3) по крайне мере одно решение заведомо имеет. И это решение очевидно: <X1= 0; X2= 0; …Xn= 0>. Это так называемое нулевое (Тривиальное) решение. Тривиальное решение у однородной системы (1.3) может оказаться единственным. Но не исключено, что у неё есть и другие (нетривиальные) решения. Сколько всего решений у различных систем линейных уравнений может быть и как их найти – об этом ниже.

Детальное рассмотрение систем линейных уравнений начнем с наиболее простой из них – с системы двух линейных уравнений с двумя неизвестными. То есть с системы вида:

(1.4)

Сколько решений (X; Y) у этой системы может в принципе быть, и как их найти? Ответ на этот вопрос можно получить, рассмотрев процесс решения системы.

Решать систему (1.4) наиболее удобно самым очевидным путем – последовательным исключением неизвестных (методом Гаусса). Этот метод состоит в следующем. Выразив из первого уравнения системы (1.4) одну неизвестную через другую (например, Y через X) и подставив ее во второе уравнение, после приведения подобных получим в итоге линейное уравнение вида Ax = B с одним неизвестным X. При этом возможны три варианта:

1) . Тогда из уравнения Ax = B однозначно находится X: , а затем по этому X однозначно находится и Y. В итоге получим единственное решение (X; Y) системы (1.4).

2) A = 0, . Тогда уравнение Ax = B оказывается противоречивым (не имеет решений). А вместе с ним не имеет решений и система (1.4).

3) A = 0, B = 0. Тогда уравнение Ax = B принимает вид и удовлетворяется при любых X. При этом для каждого конкретного значений X найдется и соответствующее ему конкретное значение Y. В итоге будем иметь бесчисленное множество (X; Y) системы (1.4).

Итак, система (1.4) в принципе может:

А) иметь одно решение;

Б) не иметь решений;

В) иметь бесчисленное множество решений.

Первый из этих случаев (единственное решение) будет осуществляться как правило. А второй и третий – как исключения. Действительно, лишь когда в уравнении Ax = B величина A окажется равной нулю, будет иметь место либо второй, либо третий случай. Во всех остальных вариантах, когда , будет иметь место первый случай.

Полученные выше выводы имеют и ясную геометрическую интерпретацию. Действительно, каждое из двух уравнений системы (1.4) представляет собой уравнение вида , а следовательно, представляет собой уравнение прямой на плоскости. Значит, решая эту систему, мы определяем на плоскости координаты (X; Y) точек пересечения некоторых двух прямых. Но таких точек у двух прямых, очевидно, может быть:

А) одна (когда прямые пересекаются);

Б) ни одной (когда прямые параллельны);

В) бесчисленное множество (когда прямые совпадают).

Соответственно этим случаям система (1.4) будет иметь или одно решение, или ни одного, или бесчисленное множество. При этом для произвольно взятых прямых случай (а) будет, очевидно, осуществляться как правило, а случаи (б) и, особенно, (в) – как исключение.

Пример 1. Найти точки пересечения прямых и .

Решение. Для нахождения этих точек составим и решим систему из уравнений указанных прямых.

Как выяснилось, данная система имеет единственное решение (; ). Значит, указанные выше прямые пересекаются в единственной точке – точке .

Пример 2. Решить систему уравнений

И дать полученному результату геометрическую интерпретацию.

– нет решений, ибо последнее уравнение остается неверным независимо от значений неизвестных Х И У. Геометрически полученный результат означает, что прямые с уравнениями и параллельны. Это подтверждается и равенством их угловых коэффициентов K1 и K2:

; K1 = 1,5

; K2 =1,5

Пример 3. Решить систему уравнений

И дать полученному результату геометрическую интерпретацию.

–

– бесчисленное множество решений. Действительно, второе уравнение системы, из которого должно было быть определено значение X, привело к правильному числовому равенству 2=2, верному независимо от X (X сократилось и исчезло из уравнения). Следовательно, величина X может быть любой. А другая неизвестная Y, если выбрано значение X, найдется по первому уравнению . В итоге получаем бесчисленное множество решений системы. Например, таких:

1) ; 2) ; 3) ; …

Все эти решения являются координатами точек пересечения тех двух прямых, уравнения которых входят в исходную систему. В силу бесчисленного количества таких точек указанные прямые совпадают.

Да, но тогда должны совпадать и их уравнения! И это действительно так: умножая на 2 обе части уравнения первой прямой, получим равносильное уравнение , полностью совпадающее с уравнением второй прямой.

Вопрос о решении системы (1.4), являющейся простейшей из систем линейных уравнений, мы исчерпали. Перейдем теперь к общему случаю (1.1), но только пока при условии, что , то есть при условии, что количество уравнений системы равно количеству ее неизвестных. Иначе говоря, перейдем к квадратным системам произвольного размера N´ N (N = 3, 4,…), то есть К системам N-го порядка вида

a11X1 + a12X2 +… + a1NXn = b1

Заметим, что при небольших N (при небольших значениях порядка системы (1.5)) неизвестные системы можно обозначать не (X1; X2; …Xn), а, например, (X; Y; Z;…). Но это, естественно, не принципиально.

Систему (1.5) произвольного порядка N, как и простейшую систему (1.4) второго порядка, наиболее естественно и просто решать методом последовательного исключения неизвестных (методом Гаусса). А именно, из первого уравнения системы выражаем какую-либо неизвестную, например X1, через остальные неизвестные (X2; X2; …Xn)

И подставляем ее во все остальные уравнения системы (второе, третье, … N-е). В итоге во всех уравнениях системы, начиная со второго, будет уже на одну неизвестную (неизвестную X1) меньше. Далее, из второго уравнения выражаем следующую неизвестную X2 через оставшиеся неизвестные (X3; X4; …Xn)

И подставляем ее во все ниже лежащие уравнения (третье, четвертое, … N-е). Ну и так далее до конца. В итоге, если не возникнет сбоев в этой схеме (каких – скажем ниже) мы преобразуем систему (1.5) к следующему равносильному треугольному виду:

(1.6)

Преобразование квадратной системы (1.5) к равносильной ей треугольной системе (1.6) называется Прямым ходом метода Гаусса.

Примечание. Мы указали лишь идею прямого хода метода Гаусса, цель которого – последовательно исключение неизвестных из уравнений системы. На практике же этой цели можно добиться и несколько иначе, причем значительно проще.

Например, чтобы исключить неизвестную X1, содержащуюся в первом уравнении системы (1.5), из второго уравнения, можно обе части первого уравнения разделить на A11, затем обе его части умножить на –A21, и после этого первое уравнение сложить со вторым. В итоге неизвестная X1 во втором уравнении исчезнет (исключится). Аналогично можно исключить неизвестную X1 и из остальных уравнений системы (третьего, четвертого, …, последнего). Далее, по аналогичной схеме, с помощью второго уравнения можно исключить из всех нижележащих уравнений неизвестную X2. И так далее до конца. В итоге мы опять придем к треугольной системе типа (1.6), но только существенно быстрее.

Кстати, неизвестную, исключаемую из других уравнений системы, часто называют Опорной неизвестной, а уравнение, содержащее эту опорную неизвестную и с помощью которого исключается эта опорная неизвестная из других уравнений системы, называется Опорным уравнением. И опорное уравнение, и опорную неизвестную удобно, для наглядности, подчеркивать.

И еще одно существенное замечание: в качестве опорной неизвестной, выбираемой на каждом этапе прямого хода метода Гаусса, удобно выбирать ту, перед которой нет числового коэффициента – только знак (+) или (–). В этом случае треугольная система типа (1.6) будет иметь другой порядок расположения неизвестных, что, конечно, не принципиально.

Пойдем далее. Будем считать, что мы (в той или иной форме) реализовали прямой ход метода Гаусса, сбоев в этой работе не было (осуществился так называемый Стандартный вариант), и нам удалось привести исходную систему (1.5) к равносильной системе типа (1.6) (или такой же, как (1.6), системе, только с другим порядком расположения неизвестных). После этого система (1.6) решается уже просто с помощью Обратного хода метода Гаусса.

Суть его в следующем. Последнее уравнение сразу дает значение неизвестной . Далее, из предпоследнего уравнения, используя найденное значение, вычисляем значение . Потом из третьего снизу уравнения, используя найденные и , находим . Двигаясь таким образом снизу вверх и дойдя до первого уравнения, последовательно определим все неизвестные системы (1.6), а значит, и неизвестные равносильной ей системы (1.5). Набор найденных значений всех неизвестных оказывается единственным, а значит, единственным окажется и полученное в итоге решение <X1; X2; …Xn> системы (1.5).

Все это будет в стандартном варианте. Но возможны и два варианта нестандартных, когда появляются сбои в изложенной выше схеме.

Нестандартный вариант 1. На каком-то этапе осуществления прямого хода метода Гаусса в каком-то из уравнений системы (или даже в нескольких уравнениях) могут исчезнуть (сократиться) все неизвестные, кроме свободных чисел, которые образуют неверное равенство типа , и т. д. Так как в этом уравнении нет неизвестных, то и невозможно сделать его верным за счет какого-то подбора неизвестных. Система, содержащая хотя бы одно такое уравнение, не имеет решений. А значит, не будет иметь решений и исходная система (1.5).

Нестандартный вариант 2. Этот вариант, в отличие от первого нестандартного варианта, будет иметь место, если на каком-то этапе прямого хода метода Гаусса в каком-то из уравнений системы все его члены сократятся, и останется верное числовое равенство . Это, кстати, может случиться и с несколькими уравнениями системы. Отбросив их, мы получим систему, в которой количество уравнений меньше количества неизвестных (получим так называемую Недоопределенную систему). Кстати, если в системе окажется два или более одинаковых уравнения, то отбросив из дублирующих друг друга уравнений все, кроме одного, мы также получим недоопределенную систему.

Завершив прямой ход метода Гаусса в недоопределенной системе, в последнем уравнении системы мы будем иметь не одну неизвестную (как это получается в стандартном варианте (1.6)), а две или более. Это последнее уравнение имеет бесчисленное множество решений, ибо в нем все неизвестные, кроме одной, можно задать произвольно (это – так называемые Свободные неизвестные), а оставшаяся неизвестная (Связанная) уже однозначно выражается через свободные неизвестные. После этого в процессе обратного хода метода Гаусса можно однозначно выразить через свободные неизвестные и остальные неизвестные системы (остальные связанные неизвестные). В итоге мы получим бесчисленное множество решений исходной системы.

Итак, подведем итог. Квадратные системы линейных уравнений вида (1.5) при любом их порядке N (N = 2,3,…) могут в принципе:

1) Иметь единственное решение (стандартный вариант).

2) Не иметь решений (нестандартный вариант 1).

3) Иметь бесчисленное множество решений (нестандартный вариант 2).

Стандартный вариант на практике встречается как правило, нестандартные – как исключения.

Пример 1. Решить квадратную систему 3-го порядка

Решение. Применим метод последовательного исключения неизвестных (метод Гаусса) по схеме, указанной в примечании выше. Опорное уравнение и опорную неизвестную на каждом шаге прямого хода этого метода будем подчеркивать.

Итак, у данной системы оказалось единственное решение (; ; ). Если подставить эти значения неизвестных в уравнения исходной системы, то можно убедиться в том, что все уравнения превращаются в верные числовые равенства. То есть решение системы найдено верно.

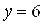
А) Прямой ход метода Гаусса:

По второму уравнению получившейся системы ясно, что система не имеет решений. Это и отмечено значком («нет решений»).

Пример 3. Решить систему

Решение. Данная система 3-го порядка однородная, так как столбец ее свободных членов состоит из одних нулей. Значит, по крайней мере, одно решение она заведомо имеет – это тривиальное решение (; ; ). Поищем возможные другие ее решения. Применим метод Гаусса.

Таким образом, у системы оказалось бесчисленное множество решений. В их число (при ) входит и тривиальное решение (; ; ).

Вопрос о квадратных системах линейных уравнений мы исчерпали. Перейдем, наконец, к общему случаю (1.1), когда в системе любое число M уравнений и любое число N неизвестных, причем, вообще говоря, . То есть перейдем к так называемым Прямоугольным системам. Естественно, следует рассмотреть и случай , и случай .

Случай M > N (количество уравнений больше количества неизвестных). Такие системы называются Переопределенными. Они, как правило, не имеют решений. Но, как исключение, они могут иметь единственное решение и даже бесчисленное множество решений. Проиллюстрируем это на примере трех уравнений с двумя неизвестными.

(1.7)

Если в этой системе отбросить какое-то (любое) уравнение, то получим квадратную систему вида (1.4) из двух уравнений с двумя неизвестными. Такая система, как мы знаем, как правило, имеет единственное решение (X; Y). Но третье (отброшенное) уравнение при этих (X; Y) вряд ли удовлетворится, если только оно не является следствием двух других уравнений. А значит, как правило, переопределенная система (1.7) из трех уравнений не будет иметь решений. Но если все же отброшенное уравнение системы (1.7) является следствием двух оставшихся, то тогда каждое решение системы из этих двух оставшихся уравнений будет и решением переопределенной системы (1.7). То есть у нее может быть и одно решение, и даже бесчисленное множество решений.

Все сказанное выше о системе (1.7) становится предельно ясным, если мы учтем, что каждое из уравнений этой системы – это уравнение прямой на плоскости. А значит, решая систему (1.7), мы ищем координаты (X; Y) общих точек трех прямых на плоскости. То есть ищем координаты точек, в которых пересекаются сразу три прямые. Но таких точек у трех произвольных прямых, скорее всего, не будет. А значит, скорее всего, система (1.7) не будет иметь решений.

Однако три прямые на плоскости все-таки могут пресекаться в одной точке, а значит, система (1.7) может иметь решение (X; Y), определяющее координаты этой точки. Более того, все три прямые могут и совпадать. Тогда у них бесчисленное количество общих точек, а значит, в этом случае система (1.7) будет иметь бесчисленное множество решений. Этими решениями будут координаты (X; Y) точек всех трех совпадающих прямых.

Пример 4. Решить систему линейных уравнений

Решение. Данная система является переопределенной (в ней три уравнения и лишь две неизвестные). Поэтому следует ожидать, что она, скорее всего, не будет иметь решений. Так ли это, выясним с помощью метода Гаусса:

Система действительно не имеет решений, так как два последних ее уравнения противоречат друг другу.

Видео:Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )

Ввод: -1,15
Результат: ( -115 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Немного теории.

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.

🎦 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Теорема о количестве решений системы линейных уравненийСкачать

Количество решений системы линейных уравненийСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Матричный метод решения систем уравненийСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Когда система имеет бесконечное количество решенийСкачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение системы уравнений методом ГауссаСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать