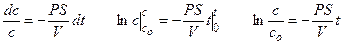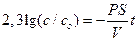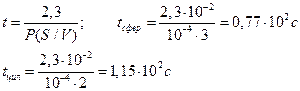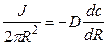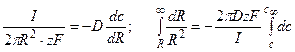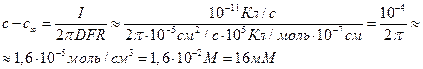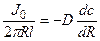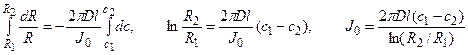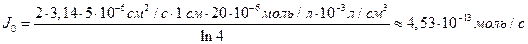Количественные законы переноса уравнения пассивной диффузии веществ ионов и неэлектролитов (4 видео)

Диффузия ионов и неэлектролитов

Диффузия представляет собой спонтанное движение растворенного вещества в сторону понижения концентрации. Диффузионные законы определяют движение незаряженных веществ в объеме (на любых расстояниях при отсутствии конвекции), перенос ионов в неперемешиваемых слоях у поверхности мембран, а также движение ионов на малых расстояниях.

Формула Стокса–Эйнштейна связывает коэффициент диффузии D с температурой T, вязкостью среды η и радиусом диффундирующих частиц r (k – константа Больцмана). Например, вязкость воды при 20°С составляет η_H_2O= 10 –3 Па∙с (1 Па = 1 Н/м 2 ).

(4.1)

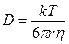
Пользуясь (4.1), можно оценить коэффициент диффузии в воде для малых молекул с радиусом

0,2 нм (10 –5 см 2 /с) или для молекул другого размера. На движение ионов в растворе влияет электрическое поле. Коэффициент диффузии иона зависит от его заряда (z):

, (4.2)

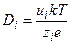
где u – подвижность иона, имеющая размерность м 2 ·с –1 ·В –1 (см 2 ·с –1 ·В –1 ), е – заряд электрона. Например, подвижности ионов K + и Na + равны 7,6·10 –4 и 5,2·10 –4 см 2 ·с –1 ·В –1 , соответственно. Из (4.1) и (4.2) получаем уравнение для расчета подвижности иона по его радиусу и заряду.

(4.3)

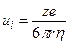
Подвижность численно равна скорости движения ионов (см/с) при напряженности поля 1 В/см.

Законы Фика описывают скорость диффузии вещества, а также пространственное распределение концентрации диффундирующего вещества в различные моменты времени.

Первый закон Фика связывает поток вещества J с коэффициентом диффузии D и градиентом концентрации (dc/dx). Размерность потока – моль∙см –2 ∙с –1 ).

(4.4)

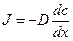
В случае диффузии через тонкую мембрану

, (4.5)

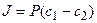
где P=Dg/h – проницаемость, h – толщина мембраны, g – коэффициент распределения вещества между водной и липидной фазами, а 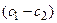– разность концентраций диффундирующего вещества в объемных фазах по разные стороны мембраны.

Второй закон Фика описывает направление изменений концентрации вещества во времени (dc/dt) в зависимости от знака второй производной (d 2 c/dx 2 ), определяющей вогнутость или выпуклость профиля концентрации по координате x:

(4.6)

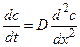
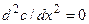
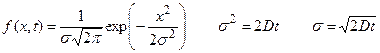
Из (4.6) в частности следует, что в случае одномерной стационарной диффузии (т.е. при dc/dt=0) профиль концентрации линеен: . В общем случае одномерной диффузии пространственно-временное распределение вещества описывается нормальным распределением Гаусса:

(4.7)

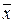
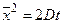
где x – координата, f(x,t) – функция распределения, σ – среднеквадратичное отклонение для нормального распределения вещества относительно исходной точки при x = 0, σ 2 – дисперсия, а t – время. Область, расположенная между координатами ±σ, содержит более 68% от общего количества диффундирующего вещества. Согласно уравнению Эйнштейна, величина σ, обозначаемая также или ‹x›, служит мерой расстояния, на которое распространяется диффундирующее вещество за определенный промежуток времени t:

, (4.8)

где 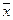– среднеквадратичное отклонение (диффузионная длина).

Пример 4.1. После инъекции в клетку некоторого вещества до концентрации c_o, клетку отмывают средой, не содержащей этого вещества. Какое время инкубации необходимо, чтобы внутренняя концентрация вещества понизилась в 10 раз, если проницаемость мембраны для этого вещества составляет 10 –4 см/с? Решить задачу для клетки сферической формы с диаметром 200 мкм и для цилиндрической клетки с диаметром 200 мкм и длиной 1 см.

Решение: При записи первого закона Фика учтем, что диффузия происходит через тонкую мембрану и, что концентрация во внешнем растворе равна нулю.

где с – концентрация вещества в клетке в момент времени t. Зная поток вещества через мембрану и геометрию клетки (площадь поверхности S и объем V), можно выразить изменение внутренней концентрации dc за промежуток времени dt:

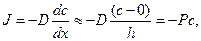
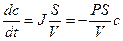
Решение этого дифференциального уравнения описывает кинетику изменения концентрации вещества внутри клетки:

, где .

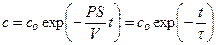
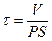
Уравнение решают методом разделения переменных и интегрирования по времени от нуля до t при соответствующем изменении концентрации от c_o до c.

Для ответа на вопрос задачи удобно перейти к десятичным логарифмам:

Отношение S/V определяется геометрией клетки. Для сферы и цилиндра оно составляет соответственно

и .

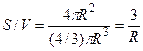
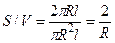
С учетом условия задачи c/c_o = 0,1 и R = 0,01 см, находим искомое время t:

Аналогичный подход используется для случаев, когда в момент времени t = 0 в наружный раствор добавляют проникающее вещество, которое начинает поступать внутрь клетки, причем наружная концентрация остается постоянной (c_o = const) из-за большого объема среды по сравнению с объемом клеток. В таком опыте моменту времени t = 0 соответствует внутренняя концентрация с = 0, а произвольному моменту времени t соответствует внутренняя концентрация с. В этом случае интегрирование дифференциального уравнения приводит к следующему решению:

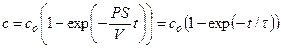
Пример 4.2. Предположим, что через калиевый канал с устьем R = 10 Å протекает ток I силой 10 пА (рис. 4.1.). При этом концентрация К + в устье повышается по сравнению с объемом раствора. Найти концентрацию в области устья канала, если концентрация К + в объеме составляет 10 мМ. При расчете принять, что коэффициент диффузии К + в воде

Решение: На выходе из канала суммарный поток переносимых ионов диффундирует во всех направлениях, ограничиваемых полусферой. Выделим элемент поверхности полусферы и запишем поток через единицу поверхности, пользуясь первым законом Фика.

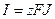
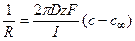
Суммарный поток вещества J связан с электрическим током I соотношением , где F – число Фарадея. Отсюда получим

, где z =1

Следовательно, перепад концентрацией между устьем канала и объемом раствора составит

Соответственно, концентрация в устье канала c_x составит 26 мМ.

Пример 4.3. Концентрация Са 2+ в питательном растворе на расстоянии 300 мкм от поверхности корня составляет 100 мкМ, а у поверхности корня с диаметром 200 мкм – 80 мкМ. Оценить диффузионный поток Са 2+ к поверхности корня на 1 см его длины (моль·с –1 ), а также поток Са 2+ на единицу поверхности корня (моль·см –2 ·с –1 ) в предположении, что коэффициент диффузии D = 5·10 –6 см 2 /с.

Решение: Обозначим суммарный диффузионный поток для сегмента корня длиной l символом J₀. Поток Са 2+ направлен радиально из объема среды к центру корня. Поток через единичный участок цилиндрической поверхности неперемешиваемого слоя на расстоянии R от центра корня составит J₀/(2πRl). Запишем уравнение первого закона Фика в радиальных координатах:

Решая уравнение, находим формулу для расчета потока по концентрациям на разном удалении от центра корня (концентрации с₁ и с₂ для радиальных расстояний R₁ и R₂).

В расчете на единицу поверхности корня поток составит

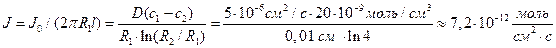
Видео:27. Уравнения переносаСкачать

Пассивный транспорт (диффузия)

Поскольку при данном виде транспорта энергия транспортируемого вещества уменьшается, то его перенос идёт только в одном направлении по концентрационному или электрохимическому градиенту. В соответствии с законом Фика диффузия прямо пропорциональная градиенту концентрации вещества, площади диффузионной мембраны, коэффициенту распределения и обратно пропорциональной толщине мембраны.

Основная количественная характеристика, используемая при описании переноса ионов или незаряженных частиц (неэлектролитов) через мембраны- это поток.

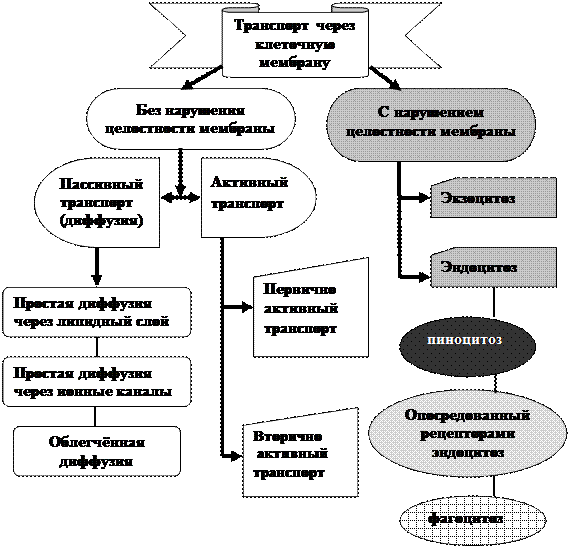Количественные законы переноса уравнения пассивной диффузии веществ ионов и неэлектролитов

Рис.3.15. Виды транспорта веществ через клеточную мембрану

Поток вещества Ф измеряют не в числе частиц, а в числе молей данного вещества . Трансмембранные потоки ионов имеют направление нормальное к поверхности мембраны. Плотность потока (J, моль/с▪м 2 ) – это количество вещества, переносимого в секунду через единицу площади, расположенной нормально потока ( к поверхности мембраны). Положительным считается направление потока из замкнутого пространства наружу. Поэтому поток из клетки в окружающую среду имеет знак «+», а поток в клетку имеет знак «-» . Величина J зависит от концентрации переносимых веществ по обе стороны мембраны (С₁ и С₂) , а в случае ионов – так же от разности потенциалов между водными фазами, омывающими мембрану φ₁ и φ_2: ∆φ= φ_2: — φ₂₁. В конечном счёте обе характеристики (потенциал и концентрация) влияют на поток потому, что от них зависит энергия ионов (молекул) в данном растворе. Энергия моля ионов данного вида в среде носит название электрохимического потенциала иона и равна: μ=μ о + RTlnC+zFφ, где μ о – стандартный химический потенциал, определяемый энергией взаимодействия иона с молекулой среды;R- газовая постоянная; Т- абсолютная температура; С- молярная концентрация, z- безразмерный заряд иона, F- число Фарадея; φ – потенциал в данной области среды.

возможность изменения конфигурации цепей жирных кислот. Ион попадает в полость, образуемую за счёт соответствующих изгибов окружающих цепей жирных кислот. Такая полость называется кинком (от англ kink – петля, изгиб). Кинки образуются в результате теплового движения молекул и ион может перемещаться в липидном слое мембраны, перескакивая с одного кинка на другой (рис. 3.6.). Случайные тепловые движения молекул приводят к тому, что вещества из области высоких концентраций переносятся в область более низких.

Простая диффузия через липидный слой (рис. 3.6.) обеспечивает трансмембранный перенос веществ, которые имеют достаточно высокий коэффициент распределения между водной и липидными фазами. К таким веществам относятся: жирорастворимые вещества и незаряженные полярные молекулы (ряд гормонов, алкоголь, мочевина, О₂, СО₂ и др.). Большое значение для растворения в липидном слое и перенос через него молекул и ионов играет

Проницаемость клеточной мембраны для многих веществ ограничена не только липидным бислоем, но и прилегающими к мембране неперемешивающимися слоями воды, которые вместе с клеточной мембраной в совокупности ведут себя как последовательно соединённые электрические соединения. В свою очередь движение жидкости в клетке и вне её зависит от тканевого метаболизма. Если жидкость внутри клетки и в межклеточной среде интенсивно движется, то толщина примембранного слоя воды может превышать толщину самой клеточной мембраны в 100-300 раз. В то же время вязкость клеточной мембраны (благодаря липидам) в 10-100 раз выше вязкости воды. Следовательно, коэффициенты диффузии иона в воде и мембране относятся друг к другу как 30-100 к единице. Отсюда следует, что в коэффициенте распределения вещества в системе мембрана/вода решающую роль играет липофильность молекулы (иона). Если для К + , Na + , Cа 2+ примембранные слои воды практически не влияют на общую проницаемость: основная барьерная функция принадлежит липидному бислою мембраны, то для нейтральных молекул (например кислорода) роль примембранных слоёв воды для его трансмембранного проникновения в клетку становится заметной.

Простая диффузия через ионные каналы мембраны(рис. 3.17.) даёт возможность проходить через клеточную мембрану веществам, обладающим низким коэффициентом распределения между липидной и водной фазами, следовательно, не растворяющихся в липидах. Например, вода, которая проходит сквозь мембрану клетки, благодаря наличию в ней специальных каналов (аквапоринов), расположенные в бислое липидов. При этом вода переходит из менее концентрированного раствора в более концентрированный. Через ионные каналы могут диффундировать малые незаряженные молекулы, в том числе, и способные одновременно проходить через липидный бислой (этанол, мочевина, О₂, СО₂ и др). Следует отметить избирательность ионных каналов для незаряженных катионов и анионов.

Ионные каналы клеточной мембраныпредставлены интегральными белками, которые образуют поры в липидном бислое клеточной мембран.

Селективность (избирательность) канала определяется диаметром поры и энергией дегидратации иона. Диаметр поры несколько больше диаметра иона в кристаллическом состоянии. Малые размеры поры делают необходимым снятие с проходящего через мембрану иона его «водной шубы», т.е. осуществлять его временную дегидратацию.

Проницаемость канала регулируется а) изменением мембранного потенциала (потенциалуправляемые каналы); б) влиянием биологически активного вещества (гормоны, медиаторы, Са 2+ ) на канальный белок (рецепторуправляемые каналы).

Для ионного канала характерны три физиологических состояния: покой (потенциальной активен), открыт ( активирован) и закрыт (инактивирован).

1.Специфичность транспорта, т.е переносчик связывает определённое вещество или небольшую группу родственных веществ; 2. Зависимость скорости трансмембранного переноса вещества от субстратного насыщения.Высокие нарастающие концентрации переносимого вещества приводят к вовлечению в процесс транспорта всех его переносчиков, в результате чего скорость трансмембранного переноса перестаёт увеличиваться.

Облегчённая диффузия (рис. 3.18.) характерна для большинства полярных молекул (сахара, аминокислоты, нуклеотиды и т.д.), для которых липидный бислой мембраны плохо проницаем. Поэтому в процессе эволюции сформировался особый транспорт таких веществ через клеточную мембрану, осуществляемый с участием специфических мембранных белков переносчиков, которые и помогают (облегчают проникновение) этим веществам прохождение через мембрану клетки. Облегчённую диффузию отличает от простой следующие особенности:

3. Наличие специфических стимуляторов и ингибиторов облегчённой диффузии. Например, инсулин активирует облегчённую диффузию глюкозы в жировые и мышечные клетки.

Активный транспорт

Данный вид переноса вещества через клеточную мембрану сопряжён с затратой энергии, благодаря чему он даёт возможность переносить вещества против градиента их концентрации, т.е. из зоны меньшей в зону большей концентрации. В качестве источника энергии в клетки используются : энергия связей аденозинтрифосфорной кислоты (АТФ) и энергия трансмембранных ионных градиентов. В зависимости от вида используемой энергии различают два вида активного транспорта: первично активный транспорт (используется энергия АТФ) и вторично активный транспорт(используется энергия электрохимического градиента Na + ).

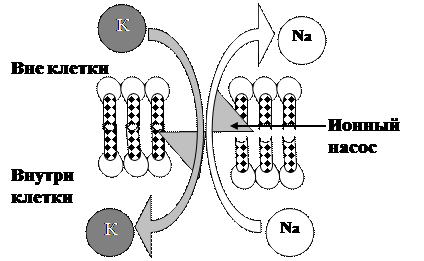
Первично активный транспортосуществляется в результате деятельности ионных насосов, белковый комплекс которых обладает свойствами переносчика (для транспортируемого вещества) и фермента, расщепляющего АТФ, энергия которого используется насосом для транспорта (рис.3.19.).

Рис.3.19. Схема первично активного транспорта через клеточную мембрану

В настоящее время в клетке обнаружены следующие насосы, использующие энергию АТФ: Na + ,К + -насос (Na + ,К + -АТФаза) имеется в плазматической мембране всех клеток организма человека. Энергия АТФ затрачивается на удаление из клетки Na + и возвращения туда К + , проникших путём простой диффузии. Са 2+ -насос (Са 2+ -АТФаза)как в плазматической мембране, так и мембранах клеточных органелл (например, цистерны в миоцитах). Насос откачивает кальций из цитозоля клетки либо во внеклеточную среду, либо в его внутриклеточные депо. Наличие данного насоса обусловлено той важной ролью, которую играет кальций в жизнедеятельности клеток. Протонный насос (Н + -АТФаза)имеется как в плазматической мембране, так и мембранах некоторых клеточных органелл.

Вторично активный транспорт(рис.3.20.) использует энергию градиента концентрации Na + созданного К + ,Na + -насосом. Ионы натрия и транспортируемые вещества связываются с молекулой белка переносчика мембраны. Натрий, перемещением внутрь клетки по электрохимическому градиенту «тащит» за собой вещества (например моносахара и аминокислоты), которые могут переносится против градиента концентрации. Внутриклеточный натрий откачивается Na + ,К + — насосом, благодаря чему восстанавливается электрохимический градиент натрия и цикл повторяется снова.

Вне клетки

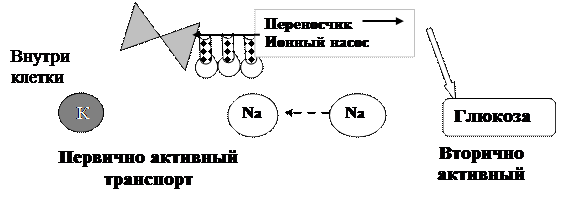Рис. 3.20. Схема вторично активного транспорта через клеточную мембрану

Эндоцитоз и экзоцитоз

Данные виды трансмембранного переноса веществ в клетку и из неё сформировались в процессе эволюции и предназначены для крупномолекулярных веществ не способных перемещаться через клеточную мембрану разобранными выше способами.

Эндоцитоззаключается в поступлении вещества из внеклеточной среды в клетку в составе мелких или крупных пузырьков, образовавшихся из участков плазматической мембраны, в которых и заключено транспортируемое вещество. Эти пузырьки либо сливаются в клетках с органеллами (лизосомами), где происходит переваривание поступивших путём эндоцитоза веществ, либо они транспортируются на противоположный полюс клетки и выделяют воё содержимое во внеклеточную среду путём экзоцитоза.

Различают три вида эндоцитоза:

1. пиноцитоз (неспецифических захват внеклеточной жидкости и растворённых в ней веществ)

2. опосредованный рецепторами эндоцитоз (связывание веществ со специфическими рецепторами на клеточной мембране с образованием окаймлённых пузырьков ( эндосом).

3. фагоцитоз(захват крупных частиц «профессиональными клетками» фагоцитами- нейтрофилы, моноциты, макрофаги)

Экзоцитоз –процесс выделения клеткой веществ во неклеточную среду. Он существует во всех клетках, но особенно он важен для нервных клеток (выделение медиаторов), клеток эндокринной системы (выделение гормонов) и клеток желёз внешней секреции (выделение пищеварительных соков). Выделение вещества из клетки происходит в составе экзоцитозных пузырьков, образующихся в специальной клеточной органелле (аппарат Гольджи). Пузырьки транспортируются с помощью микрофиламентов и микротрубочек к клеточной мембране, сливаются с ней, а их содержимое выделяется во внеклеточную среду.

Жизненный путь клетки

Клеточный цикл неполовых клеток состоит из интерфазы и митоза. Интерфаза включает в себя последовательно протекающие периоды G₁, (G₀)S, и G₂. Период G₁ следует за митозом. Длительность от нескольких часов до суток. После периода G₁ наступает либо период G₀, либо S. В период G₀ клетка может выйти из цикла и либо: 1. Быть длительно неактивной (например, клетки иммунной памяти); 2.Функционировать как обычная дифференцированная клетка (например, гепатоцит) в обычных условиях; 3) Достигать необратимой дифференцировки (например, нейроны и кардиомиоциты). Если клетка переходит из периода G₁ в период S (синтетический период), то через 8-12 часов переходит в премитотический период G₂. который длится 2-4 часа и затем переходит в митоз. Митоз состоит из следующих фаз: профаза, метафаза, анафаза и телофаза. В ходе митоза из материнской клетки образуются две дочерние клетки, идентичные материнской.

Физиологическая гибель клетки (апопотоз) -это активный, генетически запрограммированный процесс. Пусковыми факторами апоптоза являются: нарушение рецепторного аппарата клетки, активные формы кислорода, этанол, низкокалорийную диету и т.д.. Существуют два пути его активации.

Первый путь реализуется через активацию специального гена, который запускает апоптоз путём остановки клеточного цикла и торможения ферментов, отвечающих за репарацию повреждённого участка ДНК. При этом актируются гены, кодирующие синтез белков-стимуляторов апопотоза, которые активируют ферменты, повреждающие структуры клетку и приводящие тем самым её к гибели. В клетке существуют и «гены-спасатели», кодирующие белки, тормозящие апоптоз.

Второй путь реализации апоптоза заключается в появлении на мембране стареющих клеток специального белка, к которому вырабатываются антитела, адсорбирующиеся на мембранах клеток с образованием комплекса белок-апоптоза + антитело. При его контакте с фагоцитом стареющая клетка, несущая данный комплекс, прикрепляется к мембране фагоцитирующей клетки и поглощается ею. Данный процесс получил название аутофагоцитоза.

Физиологическое значение апоптоза:

1) регуляция развития тканей и органов в период внутриутробного развития;

2) инволюция зрелых органов и тканей,

3)регуляция популяции клеток: уничтожения старых и генетически изменённых клеток в зрелых тканях.

Уменьшение способности к апоптозу ниже физиологического уровня –путь к аутоиммунным заболеваниям и злокачественному перерождению клеток.

Видео:Закон диффузии ФикаСкачать

Транспорт неэлектролитов через клеточные мембраны. Простая диффузия. Уравнение Фика. Облегченная диффузия: механизмы, транспорта (подвижные, фиксированные переносчики), отличия от простой диффузии

Живые системы на всех уровнях организации — открытые системы, поэтому транспорт веществ через биологические мембраны — необходимое условие жизни. Большое значение для описания транспорта веществ имеет понятие электрохимического потенциала.

Химическим потенциалом данного вещества называется величина, численно равная энергии Гиббса, приходящаяся на 1 моль этого в-ва.

Математически химический потенциал определяется как частная производная от энергии Гиббса G по количеству k-го вещества, при постоянстве температуры Т, давления Р и количеств всех других веществ m1:

м (мю) = (dG/dmk)Р,Т,m1

Для разбавленного раствора:

м = м0 +RTlnC, где м0 — стандартный химический потенциал, численно равный химическому потенциалу данного вещества при его концентрации 1 моль/л в растворе.

Электрохимический потенциал — величина, численно равная энергии Гиббса G на 1 моль данного вещества, помещенного в электрическое поле.

Для разбавленных растворов

м (мю с черточкой) = м0 + RTlnC + zFф(фи), где F = 96500 Кл/моль — число Фарадея, z — заряд иона электролита.

Транспорт веществ через биологические мембраны можно разделить на 2 основных типа: пассивный и активный.

Пассивный транспорт — это перенос вещества из мест с большим значением электрохимического потенциала к местам с его меньшим значением. Пассивный транспорт идет с уменьшением энергии Гиббса, и поэтому данный процесс может идти самопроизвольно без затраты энергии.

Диффузия — самопроизвольное перемещение вещества из мест с большей концентрацией в места с меньшей концентрацией вещества вследствие хаотического теплового движения молекул. Диффузия вещества через липидный бислой вызывается градиентом концентрации в мембране. Плотность потока вещества по закону Фика:

Jm = -DdC/dx = -D(Cm2 — Cm1)/1 = D(Cm1 — Cm2)/1,

где Cm — концентрация вещества в мембране около каждой поверхности, 1 — толщина мембраны.

В биологических мембранах был обнаружен еще один вид диффузии — облегченная диффузия. Облегченная диффузия происходит при участии молекул-переносчиков. Облегченная диффузия происходит от мест с большей концентрацией переносимого вещества к местам меньшей концентрацией. По-видимому, облегченной диффузией объясняется также перенос через биологические мембраны аминокислот, сахаров и других биологически важных веществ.

Отличия облегченной диффузии от простой:

перенос вещества с участием переносчика происходит значительно быстрее;

облегченная диффузия обладает свойством насыщения: при увеличении концентрации с одной стороны мембраны плотность потока вещества возрастает лишь до некоторого предела, когда все молекулы переносчика уже заняты;

при облегченной диффузии наблюдается конкуренция переносимых веществ в тех случаях, когда переносчиком переносятся разные вещества; при этом одни вещества переносятся лучше, чем другие, и добавление одних веществ затрудняет транспорт других;

есть вещества, блокирующие облегченную диффузию — они образуют прочный комплекс с молекулами переносчика.

Разновидностью облегченной диффузии является транспорт с помощью неподвижных молекул-переносчиков, фиксированных определенным образом поперек мембраны. При этом молекула переносимого вещества передается от одной молекулы переносчика к другой, как по эстафете.