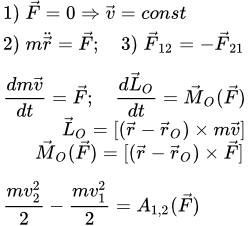Колебания при наличии сил вязкого трения уравнение движения и закон движения

Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы F и силы вязкого сопротивления R (рис. 14.5). Будем считать, что модуль силы сопротивления пропорционален первой степени скорости (R =_р V, где р — коэф- фициент сопротивления) и направлена сила R противоположно вектору V, следовательно, R =-aV.

Совместим начало координат с точкой О (положением равновесия точки). Тогда для произвольного положения М F_x= —сх, R_x = = -pi и дифференциальное уравнение движения точки будет

После деления обеих частей уравнения на т и переноса всех его членов в левую часть получим дифференциальное уравнение свободных колебаний при сопротивлении, пропорциональном скорости,

Легко убедиться, что величины к и b имеют одинаковые размерности (1/вре- мя), что позволяет их сравнивать друг с другом. При таких сравнениях следует иметь в виду, что параметр b характеризует силу сопротивления среды, а параметр к — восстанавливающую силу.

Решение уравнения (14.11) ищут в виде х = Се 9 ‘. Подставив эту функцию х в (14.11), получим для определения параметра q характеристическое уравнение q 2 + 2 bq + к? — О, корни которого будут

Характер движения точки существенно зависит от соотношения величин b и к.

Случай малого сопротивления <Ь Ь( ,значения которого с течением времени убывают, стремясь к нулю. Колебания, происходящие по законам (14.15), (14.16), называются затухающими. График этих колебаний показан на рис. 14.6 (он заключен между пунктирными кривыми х = A_xz

bt ). Важно отметить, что максимальные отклонения точки от положения равновесия уменьшаются с течением времени, а промежуток времени т, между каждыми двумя последовательными максимальными отклонениями (одного знака) или прохождениями положения статического равновесия в одном направлении (см. рис. 14.6) есть постоянная величина (ее называют условным периодом затухающих колебаний); она равна периоду функций sin(A:₁/ + о^):

Из сравнения формул (14.17) и (14.8) заключаем, что период затухающих колебаний Т] больше периода собственных колебаний при отсутствии сопротивления. Однако при небольшом сопротивлении, когда Ь ы называют условной амплитудой. Последовательные значения максимальных отклонений от центра колебаний (см. рис. 14.6) будут убывать по закону геометрической прогрессии. Знаменатель этой прогрессии е — * 1 ‘ называется декрементом рассматриваемых колебаний, а модуль его натурального логарифма, т. е. величина Ьх_х — логарифмическим декрементом затухающих колебаний.

Таким образом, основное влияние малого сопротивления на свободные колебания материальной точки выражается в уменьшении амплитуды колебаний по закону геометрической прогрессии.

Постоянные интегрирования С,, С₂ в выражении (14.15) и соответственно А_<, а, в выражении (14.16) определяются из начальных условий: при t = 0 х = х₀, х = х₀ по формулам

Случай большого сопротивления (b > к). В этом случае, согласно формуле (14.13), корни характеристического уравнения будут оба действительными и отрицательными, и поэтому решение уравнения (14.11) принимает вид

Как видим, в решение входят функции, которые не являются периодическими и со временем монотонно убывают, стремясь к нулю. Движение точки не будет колебательным, и она под действием восстанавливающей силы будет асимптотически приближаться к равновесному положению.

График движения в зависимости от начальных условий будет иметь вид одной из кривых, представленных на рис. 14.7.

Случай критического сопротивления (Ь = к). Корни характеристического уравнения по формуле (14.13) будут равными друг другу отрицательными числами #i = q₂ — — b и решение уравнения (14.11) примет вид:

Движение точки в этом случае не будет колебательным, а графики движения в зависимости от начальных условий будут аналогичны кривым, показанным на рис. 14.7.

Задача 14.2. Цилиндр массой т и радиусом г, частично погруженный в вязкую жидкость с удельной плотностью у (рис. 14.8), выводят из равновесного положения, сообщая ему некоторое вертикальное перемещение. Определить период последующих затухающих колебаний цилиндра, считая, что при движении на него действует сила вязкого трения R =-iV.

Решение. В положении статического равновесия_ (рис. 14.8, а) на цилиндр действуют сила тяжести Р и архимедова сила N₀, значение которой равно весу вытесненной жидкости, т. е. N_<) = ул/* 2 /г₀ (л/* 2 — площадь дна, /?₀ — высота погруженной в жидкость части цилиндра при равновесии).

Отсчитываем координату х по вертикали вниз от положения статического равновесия. В произвольный момент времени (рис. 14.8, б) на цилиндр действуют: сила тяжести Р, архимедова сила N, причем N — = ynr 2 (h₀ + х) = N₀ + улг 2 х, и сила сопротивления R (считая, что цилиндр двигается вниз, т. е. х>0, получим направление силы R вверх и R_x = -рх). Составим дифференциальное уравнение поступательного движения цилиндра в проекции на ось х

Учтя, что в положении статического равновесия (см. рис. 14.8, a) P—N₀ — 0, и введя обозначения

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Колебания материальной точки при наличии вязкого трения

В реальных условиях колеблющаяся материальная точка всегда испытывает сопротивление движению. Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы и силы вязкого сопротивления.

Дифференциальное уравнение колебаний при действии восстанавливающей силы 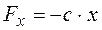и силы сопротивления имеет следующий вид:

;

получим дифференциальные уравнения свободных колебаний при наличии вязкого сопротивлении

,

Коэффициент k – круговая частота – характеризует восстанавливающую силу, а коэффициент h характеризует силу сопротивления. Эти коэффициенты сопоставимы и имеют размерность 1/с.

Колебательный процесс существенно зависит от соотношения величин h и k.

Рассмотрим несколько случаев.

1. Случай малого сопротивления (h

Пусть на материальную точку действуют восстанавливающая сила и возмущающая сила . При этом величина k будет являться угловой частотой собственных колебаний, а величина p – угловой частотой вынужденных колебаний. Силу сопротивления мы не учитываем.

Дифференциальное уравнение вынужденных колебаний:

;

,

где — приведенная амплитуда возмущающей силы.

Уравнение движения в зависимости от соотношения величин k и p имеет различный вид. В случае, когда ,

,

где ,

Амплитуда чисто вынужденных колебаний:

.

С другой стороны, воспользовавшись уравнениями , получим :

.

Величина называется коэффициентом динамичности. Данный коэффициент показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение при действии максимальной возмущающей силы H.

Рассмотрим случай, когда . Уравнение движения при этом будет такое же как и в предыдущем случае. График колебаний представлен на рис.3.13.

Такое движение называется биением.

Случай, когда . Уравнение движения:

.

График колебаний представлен на рис.3.14.

При таком движении происходит неограниченный рост амплитуды со временем. Это явление носит название резонанса. При резонансе коэффициент динамичности стремится к ∞ .

Решение задач

Условие задачи. Стержень OA длины l, на конце которого помещен груз массы m, может поворачиваться относительно оси O (рис. 3.15). На расстоянии a от оси O к стержню прикреплена пружина с коэффициентом жесткости c. определить круговую частоту колебаний груза, если стержень в положении равновесия занимает горизонтальное положение. Массой стержня пренебречь.

Решение. Круговую частоту колебаний груза определим по формуле

. (3)

Для этого сначала найдем эквивалентную жесткость эквивалентной пружины.

Рассмотрим равновесие груза A, укрепленного на стержне. Уравнение моментов относительно точки O сил, действующих на груз, будет иметь следующий вид:

,

где — сила упругости пружины в положении равновесия груза. Откуда

. (4)

Рассмотри теперь равновесие груза A на эквивалентной пружине. Уравнение равновесия груза имеет следующий вид:

,

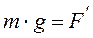
где — сила упругости эквивалентной пружины в положении равновесия груза. С учетом этого получим

(5)

Приравнивая правые части выражений (4) и (5), получим

. (6)

Отношение найдем как отношение сторон a и l соответственно треугольника OAB:

. С учетом этого выражение (6) примет вид

.Найденное значение подставим в формулу (1):

.

ПРИМЕР 2. Найти период свободных вертикальных колебаний корабля на спокойной воде, если масса корабля М т, площадь его горизонтальной проекции S м 2. Плотность воды ρ= 1 т/м 3 . Силами, обусловленными вязкостью воды, пренебречь.

РЕШЕНИЕ. В процессе вертикальных колебаний на корабль действуют две силы: сила тяжести M g и выталкивающая корабль из воды сила Архимеда F_A. Условно, изобразим корабль в двух положениях (рис. 3.15); положении статического равновесия 1 и в произвольном положении 2 определяемом координатой x.

Составим дифференциальное уравнение движения центра тяжести корабля:

Получено уравнение вида ,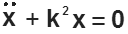

где

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Динамика материальной точки. Все законы и теоремы

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Законы динамики

Первый закон Ньютона (закон инерции Галилея)
Существуют такие системы отсчета, относительно которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если точка покоилось в определенный момент времени, то она будет покоиться и в последующие моменты.

Не во всех системах отсчета выполняется закон инерции. Например, если мы выберем систему отсчета, связанную с ускоряющейся ракетой, то относительно этой системы, не взаимодействующие материальные точки, не будут двигаться прямолинейно и равномерно.

Инерциальная система отсчета – это система отсчета, в которой справедлив закон инерции.
Движение по инерции – это движение точки, совершаемое при отсутствии действующих на нее сил.

Второй закон Ньютона (основной закон динамики)
Взаимодействие на выбранную материальную точку со стороны других тел описывается вектором, который называется силой. При этом, в инерциальных системах отсчета, действие силы приводит к ускорению точки , которое пропорционально приложенной силе, имеет одинаковое с ней направление, и обратно пропорционально массе точки:
(1) .

Если есть радиус-вектор, проведенный из начала координат к точке, то ускорение есть вторая производная радиус-вектора по времени:
.
Производную по времени, в теоретической механике, обозначают точкой над переменной, а не штрихом, как в математическом анализе.

Если на точку действует не одна, а n сил, то в правой части производится суммирование по всем силам, действующих на точку. Тогда уравнение (1) примет вид:
(2) .

Третий закон динамики (закон равенства действия и противодействия)
Если две материальные точки действуют друг на друга, то сила, с которой первая точка действует на вторую, равна по абсолютной величине и противоположна по направлению силе, с которой вторая точка действует на первую. При этом силы направлены вдоль прямой, соединяющей точки.

Закон независимости сил
Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.

То есть уравнение (2) можно записать в виде:
, где .

Видео:Урок 325. Колебательное движение и его характеристикиСкачать

Задачи динамики

Первая задача динамики
Зная закон движения точки, определить действующую на нее силу.

Вторая (основная) задача динамики
Зная действующие на точку силы, определить ее закон движения.

Видео:Сила тренияСкачать

Основные виды сил

Единицей измерения силы в СИ является 1 ньютон (1 Н = кг·м/с 2 ). Это сила, которую нужно приложить к точке массой 1 кг, чтобы она получила ускорение 1 м/с 2 .

Сила тяжести.
Сила тяжести действует на любую материальную точку, находящуюся на поверхности Земли. Она пропорциональна массе точки и равна
,
где – ускорение свободного падения, направленное вниз. Его величина зависит от широты и высоты над уровнем моря. Стандартное значение, принятое при построении систем единиц, составляет м/с 2 .

Сила тяготения.
.
Здесь – массы точек, r – расстояние между ними, Н·м 2 /кг 2 – гравитационная постоянная.

Для точки массы m на поверхности Земли имеем: . Отсюда . Тогда силу тяготения Земли можно вычислять по формуле:
,
где R = 6371 км – радиус Земли; r – расстояние от точки до центра Земли.

Сила электростатического взаимодействия.
,
где – величины зарядов; r – расстояние между ними; Н·м 2 /Кл 2 – коэффициент. Одноименные заряды отталкиваются, разноименные – притягиваются.

Сила трения скольжения
возникает при скольжении одного тела по поверхности другого. Она направлена в сторону, противоположную скорости движения. Ее величина определяется по формуле:
F = fN ,
где N – сила давления, перпендикулярная поверхности, с которой скользящее тело прижимается к поверхности; f – коэффициент трения, который зависит от материалов соприкасаемых тел.

Сила упругости.
Эта сила возникает при деформации упругих тел. Это могут быть растяжения, сжатия и изгибы. Она определяется по формуле
F = cλ ,
где λ – величина деформации; c – коэффициент, который зависит от материала упругого тела. Для пружины λ – это удлинение или сжатие пружины; c – коэффициент жесткости.

Сила вязкого трения.
При движении тела в вязкой среде с небольшими скоростями, на него действует сила трения, пропорциональная скорости движения:
F = μv ,
где v – скорость тела; μ – коэффициент сопротивления.
При больших скоростях, сила трения пропорциональна квадрату скорости.

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Дифференциальные уравнения движения точки

Спроектируем уравнение (2) на оси прямоугольной системы координат. Пусть радиус вектор точки имеет в этой системе компоненты (проекции) . Тогда из векторного уравнения (2) получаем систему уравнений:
.
Это есть дифференциальные уравнения движения точки в прямоугольной системе координат.

Спроектируем уравнение (2) на оси естественного трехгранника:
.
Здесь – единичный вектор, направленный по касательной к траектории; – единичный вектор, перпендикулярный и лежащий в касательной плоскости траектории; – единичный вектор, перпендикулярный и . Поскольку , то .
Вводим пройденный путь s , измеренный вдоль дуги траектории точки. Пусть ρ – радиус кривизны траектории в рассматриваемой точке. Тогда, для естественного способа задания движения точки, уравнения движения примут вид:
.

Уравнения движения в полярных координатах для плоского движения:
.

Прямолинейное движение точки

Пусть ось x направлена вдоль линии движения точки. Тогда уравнение движения имеет вид:
(3) .
Его общее решение:
,
где – произвольные постоянные. Их находят из начальных условий:
.

Если сила F_x зависит только от времени, то из уравнения (3) сначала определяют скорость v_x , а затем координату x , последовательно интегрируя уравнения:
.
Если сила зависит только от координаты x , то выполняют преобразование:
;
;
.

Колебательное движение материальной точки

Свободные колебания

Рассмотрим движение груза на пружинке. Считаем, что груз является материальной точкой; массой пружины можно пренебречь; и отсутствует сила тяжести. Пусть движение происходит вдоль оси x . За начало отсчета выберем такое положение груза, при котором пружина не деформирована. Тогда на точку действует только восстанавливающая сила упругости пружины, которая определяется по закону Гука:
(К1) ,
где x – деформация пружины; c – коэффициент жесткости. Он равен силе, которая возникает при деформации, равной единице (один метр) и имеет размерность [Н/м]. Из (К1) видно, что сила является восстанавливающей, то есть направлена так, чтобы вернуть точку в начало координат к недеформированному состоянию. Сила такого вида возникает не только при деформации пружины, но и во многих других случаях при небольшом отклонении точки от равновесного положения.

Составим уравнение движения точки и выполняем преобразования:
.
Введем обозначение . В результате получаем.

(К2) .
Уравнение (К2) называется дифференциальным уравнением свободных колебаний. Его также называют дифференциальным уравнением гармонических колебаний. Оно является линейным однородным дифференциальным уравнением второго порядка.

Ищем его решение в виде . Получаем характеристическое уравнение:
.
Оно имеет два мнимых корня: . Тогда общее решение уравнения (К2) имеет вид:
,
где и – произвольные постоянные. Они определяются из начальных условий. Пусть – координата и скорость точки в начальный момент времени , тогда
;
.

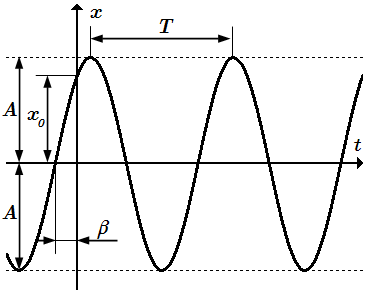
График гармонического движения точки.

Часто бывает удобно вместо постоянных интегрирования и перейти к новым постоянным A и β по формулам: . Тогда
(К3) .
Это есть уравнение гармонического колебательного движения точки. Здесь – амплитуда колебаний;
– фаза колебаний;
β – начальная фаза, ;
– циклическая частота колебаний, которую также называют угловой или собственной.
Период колебаний: .
Частота колебаний: – это число циклов колебаний, совершенных в единицу времени. Она широко применяется в технике, однако для математического описания более удобна угловая частота, которую мы будем использовать в дальнейшем и называть просто частотой.

Частота k и период T не зависят от начальных условий, а амплитуда и фаза – зависят. Кроме этого, k и T не зависят от амплитуды. Колебания, у которых частота и период не зависят от амплитуды, называют изохорными колебаниями. Если рассмотреть колебания с большой амплитудой, при которой закон Гука (К1) не выполняется, то уравнение (К2) не будет линейным и колебания не будут изохорными.

Влияние постоянной силы

Пусть теперь, наряду с восстанавливающей силой (К1), на точку действует постоянная сила P , например сила тяжести. Тогда уравнение движения примет вид:
.
Это приводит к смещению центра колебаний в сторону действия силы P на величину
δ _ст = P/c .
Это смещение называют статическим отклонением. Если P – сила тяжести, то
.

Колебания при вязком трении

Пусть на точку, кроме силы упругости пружины, действует сила сопротивления среды. При малых скоростях она пропорциональна скорости точки:
. Это так называемое вязкое трение. Составим уравнение движения:
. Обозначив μ/m= 2 b , получаем:
(К4) . Составляем характеристическое уравнение:
(К5) . Оно имеет два корня:
.

Затухающие колебания

При b , корни характеристического уравнения (К5) комплексные:
. Тогда общее решение уравнения (К4) имеет вид:
,
где . Обозначим , . Тогда
(К6) .
, ;
– амплитуда (переменная величина);
b – коэффициент затухания;
– частота затухающих колебаний;
– период затухающих колебаний. Он больше периода свободных колебаний. При небольшом коэффициенте затухания (при b/k ≪ 1 ) T ₁ &approx; T .
Колебания, происходящие по закону (К6) называются затухающими. График затухающих колебаний заключен между двумя кривыми x = &pm;Ae –bt , симметричными относительно оси t .

Затухающие колебания можно рассматривать как гармонические колебания с переменной амплитудой . Относительное изменение переменной амплитуды за период колебания называется декрементом колебаний. Он равен
. Модуль логарифма декремента называется логарифмическим декрементом. Он равен .

Апериодическое движение точки

При (или ) корни характеристического уравнения (К5) действительные. Поэтому движение точки является апериодическим.
При (или ) характеристическое уравнение (К5) имеет два различных действительных корня:
. Тогда общее решение уравнения (К4) имеет вид:
(К7) .
Сюда не входят тригонометрические функции. Поэтому это апериодическое движение. Точка может пройти через положение равновесия x = 0 не более одного раза.

Закон движения (К7) можно выразить через гиперболические функции, если положить: . Тогда
.
Перейдем к новым постоянным интегрирования A и β , выполнив подстановку:
. Тогда
.

При b = k характеристическое уравнение (К5) имеет два кратных вещественных корня . Общее решение уравнения (К4) имеет вид:
.
Движение также апериодическое. Точка может пройти через положение равновесия x = 0 не более одного раза.

Вынужденные колебания

Рассмотрим случай, когда кроме восстанавливающей силы , на точку действует возмущающая сила, меняющаяся по гармоническому закону:
(К8) . Составим уравнение движения:
.
Введем обозначение h=H/m . Разделив на m , получаем дифференциальное уравнение вынужденных колебаний:
(К9) .

Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами со специальной неоднородной частью. Его общее решение равно сумме общего решения однородного уравнения и частного (то есть любого, отличного от нулевого) решения данного уравнения:
;
;
.
Общее решение однородного уравнения: .
Ищем частное решение в виде . В результате получаем:
;
.

Коэффициент динамичности. Действие постоянной возмущающей силы величины H приводит к статическому отклонению . Периодическая возмущающая сила (К8) с амплитудой H приводит к периодическим колебаниям с амплитудой . В связи с этим вводят коэффициент динамичности: .
Он показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение.

Явление резонанса и биения

Когда частота возмущающей силы равна частоте собственных колебаний p = k , коэффициент динамичности стремится к бесконечности, амплитуда колебаний неограниченно возрастает. Это явление называется резонансом. Уравнение движения точки при p = k имеет вид:
(К10) .
Оно имеет частное решение
.
Общее решение уравнения (К10):
.
Это уравнение показывает, что амплитуда вынужденных колебаний возрастает пропорционально времени. Фаза вынужденных колебаний отстает от фазы возмущающей силы на π/ 2 .

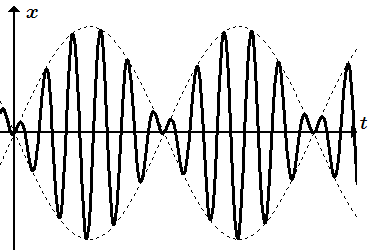
Биения.

Когда частота p возмущающей силы близка к собственной частоте k колебания точки, p/k &approx; 1 , возникает явление, называемое биениями. В этом случае частное решение уравнения (К9) имеет вид:
,
где .
Происходит наложение колебаний. Их можно рассматривать как вынужденные колебания частоты с переменной амплитудой, которая является периодической функцией с частотой .

Вынужденные колебания при наличии вязкого трения

Составим уравнение движения вынужденных колебаний при наличии вязкого трения:
.
Получаем дифференциальное уравнение:
.
Его общее решение имеет вид.
1) при b :
;
2) при b > k :
;
3) при b = k :
.
Здесь ;
ε определяется из уравнений:
.
Величины A и β являются постоянными интегрирования. Они определяются из начальных условий.

Видео:Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Общие теоремы динамики точки

Теорема об изменении количества движения материальной точки

Теорема об изменении количества движения материальной точки в дифференциальной форме
Изменение количества движения материальной точки за бесконечно малый промежуток времени dt равно элементарному импульсу равнодействующей сил, приложенных к этой точке:
.
Эту теорему можно сформулировать так:
Производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке:
(Т1) .

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если проинтегрировать уравнение (Т1) по времени от начального момента времени t = 0 до конечного момента t = t₁ , то получим теорему в интегральной форме.

Теорема об изменении количества движения материальной точки в интегральной форме
изменение количества движения материальной точки за конечный промежуток времени [0,t₁] равно импульсу силы, приложенной к этой точке, за тот же промежуток времени:
.
Здесь – скорость точки в моменты времени t = 0 и t = t ₁ , соответственно.

Теорема об изменении момента количества движения материальной точки

Теорема об изменении момента количества движения материальной точки
Производная по времени от момента количества движения материальной точки, относительно произвольного центра O , равна моменту равнодействующей силы, приложенной к точке, относительно того же центра:
.

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если на точку действует несколько сил , то равнодействующая сила равна их геометрической сумме:
.
Тогда можно записать эту теорему так:
.

Далее будем считать, что точка O выбрана в начале координат. Тогда .

Центральная сила. Второй закон Кеплера

Пусть на точку действует центральная сила с центром в начале координат O . Тогда ее момент относительно O равен нулю. По теореме об изменении момента количества движения материальной точки имеем:
.
Если ввести секторную скорость , то она оказывается постоянной
.
Получаем второй закон Кеплера (закон площадей).

Второй закон Кеплера (закон площадей)
Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью. То есть радиус-вектор точки заметает равные площади в любые равные промежутки времени.

Работа силы. Мощность

Основные понятия

Единицей измерения работы в СИ является 1 джоуль (1 Дж = 1 Н·м = кг·м 2 /с 2 ).

Работа силы при движении материальной точки от точки M ₁ до точки M ₂ равна сумме (интегралу) элементарных работ:
.
Если ввести скорость точки , то
.

Теорема о работе силы
Работа A равнодействующей силы на некотором перемещении равна алгебраической сумме работ A_k составляющих сил на том же перемещении:
.

Мощность – это величина работы, произведенная за единицу времени.
.

Единицей измерения мощности в СИ является 1 ватт (1 Вт = 1 Дж/с). Другие единицы мощности: 1 кВт (киловатт) = 1000 Вт; 1л.с.(лошадиная сила) = 736 Вт = 75 кгс·м/с.

Работа основных видов сил

Работа силы тяжести:
,
где P – сила тяжести, действующая на точку. Если начальная точка выше конечной, то работа положительна; если начальная точка ниже конечной, то отрицательна.

Работа силы упругости:
.
Здесь – деформация пружины в начальном положении; – в конечном.

Работа силы трения. Если сила трения постоянна, то
,
где s – длина пройденного точкой пути; – сила трения, которая всегда направлена в сторону, противоположную перемещению; f – коэффициент трения; N – нормальная реакция поверхности. Работа силы трения всегда отрицательна.

Работа силы тяготения.
На точку, находящуюся вблизи планеты Земля, на расстоянии r ≥ R от ее центра, действует сила притяжения
,
где R = 6371 км – радиус Земли. Тогда при перемещении точки из положения M₁ в положение M₂, сила тяготения совершит работу
.
Она не зависит от траектории движения тела.

Теорема об изменении кинетической энергии точки

Теорема об изменении кинетической энергии точки в дифференциальной форме
Дифференциал кинетической энергии точки равен сумма элементарных работ всех действующих на точку сил:
.

Проинтегрировав обе части этого уравнения вдоль траектории движения точки от положения M₁ до M₂, получим теорему в интегральной форме.

Теорема об изменении кинетической энергии точки
Изменение кинетической энергии материальной точки, при переходе ее из начального положения M₁ в конечное положение M₂, равно сумме работ всех сил, приложенных к точке на этом перемещении:
.

Силовые поля и потенциальная энергия

1. Работа сил стационарного поля при перемещении точки из положения M₁ в положение M₂ зависит только от начального положения M₁, конечного положения M₂, и формы траектории, но не зависит от закона движения точки.

2. Работа, совершенная полем при перемещении точки из положения M₁ в M₂ равна по модулю и обратна по величине работе, совершенной полем при перемещении точки из M₂ в M₁ при перемещении по той же траектории:
.

Для нестационарных полей эти свойства на выполняются.
Примеры стационарных полей: поле силы тяжести на поверхности Земли; электростатическое поле от неподвижно закрепленного заряда; поле силы упругости пружины, один конец которой закреплен.

Потенциальное силовое поле – это стационарное силовое поле, работа сил которого зависит только от начального M₁ и конечного M₂ положений точки, и не зависит от формы ее траектории. Потенциальное силовое поле также называют консервативным.

В потенциальном поле существует такая функция, через которую можно выразить вектор силы , действующей на точку.

Силовая функция – это функция, зависящая от координат точки ( x, y, z ) , через которую выражаются проекции силы потенциального поля на оси координат:
.

Отсюда следует, что сила не изменится, если к силовой функции прибавить постоянную. Таким образом, силовая функция определена с точностью до произвольной постоянной.

В потенциальном поле элементарная работа является дифференциалом от силовой функции:
.
Работа при конечном перемещении из точки в точку равна разности силовой функции в этих точках:
.
Таким образом, в потенциальном поле, работа сил поля не зависит от формы траектории. На замкнутом перемещении работа равна 0. Для более наглядной физической интерпретации, вводят понятие потенциальной энергии. Она равна, с точностью до произвольной постоянной, силовой функции, взятой с обратным знаком.

Потенциальная энергия П – это работа, которую нужно совершить при перемещении точки в потенциальном поле из данного положения в произвольным образом выбранное нулевое положение.

Так, для поля деформации, в качестве нулевого положения обычно принимают не деформированное положение; для гравитационного и электростатических полей за нулевое выбирают положение, бесконечно удаленное от тела или заряда. Для силы тяжести в поле Земли принимают любое, удобное для расчета положение. Таким образом, потенциальная энергия равна силовой функции, взятой с обратным знаком плюс постоянная, зависящая от выбора нулевого положения:
.

Пусть – нулевое положение. Тогда
;
.

Работа сил поля при перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий: .

Эквипотенциальные поверхности – это поверхности равного потенциала:
.

Сила направлена перпендикулярно эквипотенциальной поверхности.

Закон сохранения механической энергии
Если точка находится в потенциальном поле, то сумма ее кинетической и потенциальной энергий является постоянной:
.
Если на точку действуют несколько сил от разных потенциальных полей, то в качестве потенциальной энергии нужно взять сумму потенциальных энергий от каждого силового поля:
.

Основные виды потенциальных полей

В поле силы тяжести, потенциальная энергия зависит от высоты. Направив ось z вертикально вверх, получим: .

Поле силы упругости пружины. В этом поле, потенциальная энергия зависит от деформации λ пружины:
.
В качестве нулевого положения выбирают положение без деформации: λ = 0 .

Сила гравитационного притяжения и космические скорости

Между любыми двумя точками массами m ₁ и m ₂ , действует сила всемирного тяготения. Так, на точку 2 действует сила притяжения со стороны точки 1:
,
направленная вдоль прямой, проходящей через точку 1. Здесь r – расстояние между точками; Н·м 2 /кг 2 – гравитационная постоянная.

В результате притяжения, обе точки получают ускорения и движутся друг относительно друга. Мы рассмотрим более простой, но важный случай, когда масса M = m ₁ одного из тел намного больше массы m = m ₂ второго тела. Тогда точка с меньшей массой практически не оказывает влияния на движение более массивной точки. Выберем начало инерциальной системы координат в точке 1. Тогда силу гравитационного притяжения можно рассматривать как центральную силу и представить ее в векторном виде:
(П1) .
Потенциальная энергия точки 2:
(П2) .
Здесь нулевое положение выбрано на бесконечности: .

Формулы (П1) и (П2) справедливы, если объект 1 является шаром с плотностью, зависящей только от расстояния r до его центра. Пусть R – радиус такого шара. Тогда в формулах (П1) и (П2) r – это расстояние от центра шара 1 до точки 2. Они справедливы при .

Эти формулы можно использовать при расчете движения спутников вокруг Земли. Поскольку Земля вращается вокруг своей оси, то ее форма является эллипсоидом. Но в первом приближении Землю можно считать шаром радиуса R = 6371 км. Из таких допущений можно оценить космические скорости, необходимые для выведения летательных аппаратов на космические орбиты.

Первая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на круговую орбиту. Она равна км/с. Если у тела первая космическая скорость, то оно может вращаться по круговой орбите, не падая на Землю, то есть стать ее спутником.
Вторая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на параболическую орбиту. Она равна км/с. Если у тела скорость больше второй космической, то ее траекторией является гипербола, и, при отсутствии помех, оно будет удаляться от Земли и никогда не вернется назад.

Однако Солнце является той преградой, которая не даст спутнику со второй космической скоростью удалиться на бесконечное расстояние. Чтобы тело могло покинуть пределы солнечной системы, ему необходимо сообщить третью космическую скорость км/с.

Использованная литература:
А. А. Яблонский, Курс теоретической механики, часть II, динамика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 11-12-2019

🎥 Видео

Колебания в физических системах: что нужно знать для выживания и решения задач?Скачать

Урок 137. Движение тела в жидкости и газе.Скачать

Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Урок 327. Гармонические колебанияСкачать

Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Силы трения между соприкасающимися поверхностями твердых тел | Физика 10 класс #15 | ИнфоурокСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

70. Затухающие колебанияСкачать

Гармонические колебанияСкачать

Механические затухающие колебания с сухим трением | Олимпиадная физика, механика | 10, 11 классСкачать

Якута А. А. - Механика - Гармонические колебания. Собственные затухающие колебанияСкачать