| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Видео:Колебания и волны | волны | сферические волныСкачать  Колебания и волны уравнение сферической волныУравнение сферической волны В случае, когда скорость волны v во всех направлениях постоянна, а источник точечный, волна будет сферической (см. рис. 2.4.4). Предположим, что фаза колебаний источника равна ωt (т. е. φ0 = 0). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/r. Следовательно, уравнение сферической волны где А равна амплитуде на расстоянии от источника, равном единице. Уравнение (2.4.8) неприменимо для малых r, т. к. при r → 0 амплитуда стремится к бесконечности. То, что амплитуда колебаний A 1/r, следует из рассмотрения энергии, переносимой волной. 2.4.3. Фазовая скорость. Принцип суперпозиции. Групповая скорость Фазовая скорость — это скорость распространения фазы волны. Зафиксируем какое-либо значение фазы волны и проследим, с какой скоростью фаза будет перемещаться вдоль оси x: Это уравнение дает связь между t и тем значением x, где зафиксированное значение фазы будет в данный момент времени. Следовательно, dx/dt — это есть скорость перемещения данной фазы, т. к. ω = const, поэтому t — x/v = const. Возьмем производную по времени от обеих Видео:10й класс; Физика; "Уравнение плоской волны"Скачать  2.5. Сферические волныВ предыдущих разделах мы рассматривали специальный тип волн: фаза зависела только от координаты х. Волновой фронт — это нестационарная поверхность, во всех точках которой фаза волны имеет одно и то же постоянное во времени значение. Для изученных нами волн колебания среды одинаковы во всех точках плоскости, ортогональной направлению распространения волны (мы выбрали его в качестве оси х). Иными словами, фронт волны является плоскостью, параллельной плоскости, содержащей оси у, z. Фронт бегущей волны перемещается с течением времени вдоль оси х с фазовой скоростью v. Такие волны называются плоскими. Трехмерное волновое уравнение Пусть мы по-прежнему имеем дело с плоской волной. Повернем координатные оси так, чтобы направление распространения волны задавалось каким-то единичным вектором n. Решение, очевидно, имеет вид: Соотношения между Волновой вектор — это вектор, модуль которого равен волновому числу, а направление совпадает с направлением распространения волны: Фронт волны – плоскость, ортогональная волновому вектору k, – движется со скоростью v, оставаясь параллельным самому себе. Найдем уравнение, которому удовлетворяет решение (2.65). Дважды дифференцируем выражение (2.65) по координатам х, у, z: Складывая эти три уравнения, находим: Вторая производная решения по времени имеет вид: получаем из (2.67), (2.68): Выражение в скобках в левой части уравнения является дифференциальным оператором, который называется лапласианом (или оператором Лапласа) и имеет специальное обозначение Записываем волновое уравнение для волн в трехмерном пространстве в окончательной форме: Если волновая функция и зависит только от одной координаты (скажем, х), то лапласиан превращается во вторую производную по x, и мы возвращаемся к прежней форме волнового уравнения. Подчеркнем, что Но волновое уравнение (2.70) имеет и другие решения, нежели плоские волны. Простым дифференцированием можно убедиться, что сферическая волна удовлетворяет волновому уравнению. Фронт волны является сферой с центром в месте расположения источника колебаний (r = 0), причем радиус сферы увеличивается со скоростью v. Действительно, поверхность постоянной фазы дается уравнением дифференцируя которое, находим Амплитуда сферической волны убывает с увеличением расстояния до точки наблюдения. Интенсивность волны убывает по закону обратных квадратов. Это, как и закон Кулона, также связано с трехмерностью нашего пространства. Если среда не поглощает излучение, то поток энергии через поверхность сферы одинаков для сфер любых радиусов, окружающих источник излучения. Поскольку площадь сферы равна 4pr 2 , то энергия, проходящая через единицу площади, обратно пропорциональна r 2 . Стоя у полотна железной дороги, можно наблюдать следующее явление: сигнал приближающейся электрички резко меняет свой тон (частоту) в момент прохождения электрички мимо наблюдателя. Это же явление может заметить наблюдатель, сидящий в поезде и проезжающий мимо сигналящего автомобиля, стоящего на переезде. На рис. 2.18 демонстрируется аналогичное явление при движении вертолета мимо наблюдателя. Рис. 2.18. Изменение тона звука при движении вертолета мимо наблюдателя Эффект Доплера — это изменение наблюдаемой частоты волны при относительном движении источника и/или наблюдателя. Эффект назван по имени австрийского физика X. Доплера, предсказавшего его теоретически в 1842 г. Движущийся наблюдатель, покоящийся источник звука. Пусть имеется источник звука, испускающий сферические звуковые волны. На рис. 2.19 показано расположение в пространстве четырех последовательных гребней (максимумов) звуковых волн. Пусть волна имеет частоту Рис. 2.19. Эффект Доплера при движении наблюдателя Наблюдатель А движется прямо на источник звука со скоростью после предыдущего. Следовательно, для него изменяется период колебаний. Наблюдаемая частота волны равна Наблюдатель В удаляется по прямой линии от источника с той же скоростью Отсюда получаем для наблюдаемой частоты: Наконец, пусть наблюдатель Р движется со скоростью vH, составляющей угол Предыдущие формулы (2.72) и (2.73) для частных случаев получаются отсюда при На рис. 2.20 с помощью модели демонстрируется эффект Доплера для случая покоящегося источника звука и движущегося наблюдателя. Рис. 2.20. Моделирование эффекта Доплера при движении наблюдателя Движущийся источник звука, покоящийся наблюдатель. Пусть теперь наблюдатель неподвижен, а звуковые волны испускаются источником, движущимся со скоростью Рис. 2.21. Эффект Доплера при движении источника Эти гребни были испущены, когда источник звука находился в точках, отмеченных цифрами красного цвета 1, 2, 3, 4, соответственно. Иначе, точка 1 является центром сферы 1, точка 2 — центром сферы 2 и т. д. Видно, что центры соседних сфер смещаются на расстояние, проходимое источником за период колебаний Это приводит к изменению расстояния между гребнями волн, приходящих к наблюдателю. Следовательно, наблюдатель регистрирует иную длину волны. Наблюдатель А расположен так, что источник движется прямо на него. Для этого наблюдателя расстояние между гребнями волн уменьшается и равно Скорость волны не зависит от движения источника, поскольку определяется свойствами среды. Следовательно, имеем обычную связь между длиной волны и ее фазовой скоростью: Подставляя эти соотношения в (2.75), получаем откуда находим частоту n звука, воспринимаемого наблюдателем А: Для наблюдателя В расстояние между гребнями волн увеличивается и равно Аналогичные рассуждения приводят к следующему выражению для частоты звуковой волны: Наконец, для наблюдателя Р, направление на которого составляет угол Предыдущие выражения получаются отсюда при Пример 1. Наблюдатель, стоящий на платформе железной дороги, слышит гудок проходящего мимо поезда. Когда поезд приближается, частота звуковых колебаний гудка равна При скорости поезда V, скорости звука v и собственной частоте колебаний При удалении поезда воспринимаемая частота звука равна Разделив первое соотношение на второе, получаем: Отсюда находим скорость поезда: Подставляя скорость поезда в выражение (2.79), получаем оттуда: На рис. 2.22 с помощью модели демонстрируется эффект Доплера в случае движущегося источника звука и покоящегося наблюдателя. Рис. 2.22. Моделирование эффекта Доплера при движении источника Движущийся источник звука, движущийся наблюдатель. Из полученных формул можно сделать общие выводы: Выражение (2.84) явным образом нарушает принцип относительности Галилея. В самом деле, скорость Согласно принципу относительности, все наблюдаемые эффекты должны зависеть только от Пример 2. Сирена полицейской машины, стоящей на обочине дороги, издает сигнал на частоте 1 000 Гц. Определим, какой частоты звук услышит водитель, проезжающий мимо со скоростью 80 км/час. В данном случае скорость автомобиля V = 80 км/час = 22.2 м/с — это скорость наблюдателя. Скорость звука После того как водитель миновал полицейскую машину, воспринимаемая частота становится равной Пример 3. Водитель стоящей на обочине дороги машины замечает проезжающий мимо полицейский автомобиль с включенной сиреной. Найдем частоту звука, который слышит водитель, если скорость полицейского автомобиля равна 80 км/час. Полицейская сирена – та же самая, что и в предыдущем примере. Здесь скорость V = 22.2 м/с — это скорость движения источника. При приближении полиции водитель слышит сигнал частотой При удалении частота воспринимаемого сигнала равна Пример 4. Те же машины едут навстречу друг другу с равными скоростями 40 км/час = 11.1 м/с. Найдем частоты звукового сигнала при сближении и при удалении машин. Применяем формулу (2.84). При сближении воспринимается звук частотой При удалении машин сирена для водителя звучит на частоте Во всех трех случаях получились разные результаты, хотя каждый раз скорости сближения (удаления) наблюдателя и источника были теми же самыми. В то же время численные результаты близки друг к другу. Это объясняется тем, что скорости автомобилей в задаче малы по сравнению со скоростью звука. В этом случае в формуле (2.84) можно пренебречь членами и более высоких степеней. Преобразуем (2.84): Пренебрегая теперь слагаемыми, содержащими отношения квадратов скоростей, находим приближенное выражение: В (2.85) частота зависит только от относительной скорости источника и наблюдателя. Если бы формула была точна, во всех трех задачах мы получили бы один и тот же ответ: Формула (2.85) удовлетворяет принципу относительности Галилея, но она верна, строго говоря, только при бесконечно большой скорости сигнала. Нарушение принципа относительности Галилея связано с наличием среды. Действительно, при движении тел в среде можно отличить состояние покоя от прямолинейного равномерного движения хотя бы по возникающему при движении ветру. Поэтому системы отсчета при наличии среды не равноправны: из них выделена та, в которой среда как целое покоится. Рассмотрим теперь случай, когда источник звуковых волн движется со скоростью, превышающей скорость звука: Рис. 2.23. Образование конуса Маха при сверхзвуковом движении источника В каждой точке своей траектории (для простоты мы рассматриваем прямолинейное равномерное движение) источник испускал сферические звуковые волны. Волна, испущенная в момент t = 0, к текущему моменту времени t достигла точки А. Волны, испущенные на пути от S0 до St ,успели пройти меньшие расстояния. Как видно из рис. 2.23, в данный момент времени имеется коническая поверхность (ее называют конусом Маха), касательная к фронтам всех испущенных сферических волн. Эта коническая поверхность начинается от источника звука, а ее ось совпадает с направлением движения источника. Конус Маха отделяет области пространства, куда дошел звук от источника, от тех областей, куда звук не успел еще дойти. В следующий момент времени Синус угла раствора конуса определяется как отношение расстояния Коническую поверхность можно воспринимать как фронт волны (ее называют ударной). Направление распространения волны — это нормаль к фронту. Следовательно, ударная волна распространяется под углом к направлению движения источника. Соответственно, (2.86) можно записать в виде: Число Маха — это отношение Пример 5. Самолет летит горизонтально на высоте 5 000 м с постоянной скоростью. Наблюдатель заметил его у себя над головой, и засек время. Звук от самолета появился через 11 с после этого. Найдем скорость самолета и определим, на каком расстоянии по горизонтали находится самолет от наблюдателя в момент, когда последний зарегистрировал приход звука от него? За время t самолет удалился от наблюдателя на расстояние Рис. 2.24. К примеру 5. О пролете сверхзвукового самолета. Пунктирная линия – положение конуса Маха 📹 ВидеоКолебания и волны. Лекция 10. Уравнения сферической и плоской волныСкачать  механические колебания и волныСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать  74. Упругие волныСкачать  Урок 370. Механические волны. Математическое описание бегущей волныСкачать  Колебания и волны | волны | волновое уравнение | 1Скачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  Колебания и волны. Лекция 1. КолебанияСкачать  Механические колебания и все что нужно про них знать. Онлайн школа EXAMhackСкачать  Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать  Колебания и волны | волны | волновое уравнение | 3Скачать  Механические модели волн. 1.Скачать  Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  решение задач по теме механические колебания и волны 9 классСкачать  Лекция 2 ВолныСкачать  Билет №34 "Электромагнитные волны"Скачать  |

 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.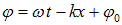

 , k и
, k и  остаются прежними.
остаются прежними.

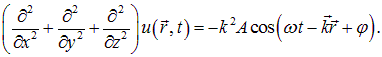


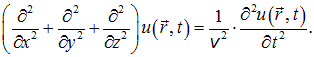
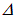 .
.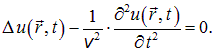


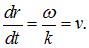
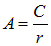


 , тогда расстояние между гребнями равно длине волны
, тогда расстояние между гребнями равно длине волны

 . Поэтому гребни волн приближаются к нему с увеличенной скоростью
. Поэтому гребни волн приближаются к нему с увеличенной скоростью  . С каждым последовательным гребнем волны наблюдатель встретится через время
. С каждым последовательным гребнем волны наблюдатель встретится через время


 (предполагаем, что
(предполагаем, что  , наблюдатель, удаляющийся от источника со сверхзвуковой скоростью, «убежит» от волны и вообще не услышит звука). Значит, гребни волн приближаются к нему со скоростью
, наблюдатель, удаляющийся от источника со сверхзвуковой скоростью, «убежит» от волны и вообще не услышит звука). Значит, гребни волн приближаются к нему со скоростью 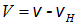 , и период колебаний равен
, и период колебаний равен
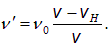
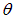 с направлением на источник. На сдвиг частоты влияет только компонента скорости вдоль линии, соединяющей наблюдателя и источник:
с направлением на источник. На сдвиг частоты влияет только компонента скорости вдоль линии, соединяющей наблюдателя и источник:
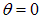 и
и 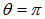 , соответственно.
, соответственно.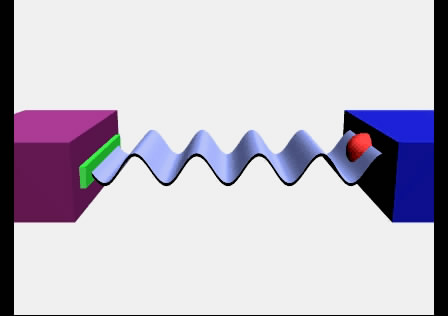
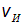 . На рис. 3.21 показано расположение в пространстве четырех последовательных гребней звуковой волны, отмеченных цифрами черного цвета 1, 2, 3, 4.
. На рис. 3.21 показано расположение в пространстве четырех последовательных гребней звуковой волны, отмеченных цифрами черного цвета 1, 2, 3, 4.
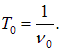

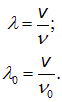
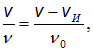
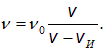

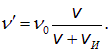
 со скоростью источника, выражение для частоты имеет вид:
со скоростью источника, выражение для частоты имеет вид: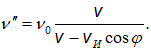
 и
и 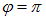 , соответственно.
, соответственно. , а когда поезд удаляется —
, а когда поезд удаляется —  . Определим скорость поезда V и собственную частоту гудка
. Определим скорость поезда V и собственную частоту гудка  . Скорость звука v предполагается известной.
. Скорость звука v предполагается известной.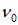 частота
частота 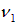 , воспринимаемая при приближении поезда, равна
, воспринимаемая при приближении поезда, равна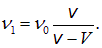

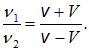


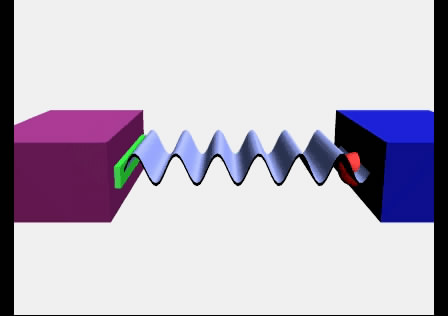

 сближения источника и наблюдателя есть сумма соответствующих проекций скоростей:
сближения источника и наблюдателя есть сумма соответствующих проекций скоростей:
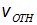 . Формула же (2.84) позволяет отделить движение наблюдателя от движения источника. Для иллюстрации рассмотрим три примера. Спешим успокоить читателя: это кажущееся недоразумение, его разъяснение приведено ниже в конце рассмотрения примера 4. С принципом Галилея всё в порядке.
. Формула же (2.84) позволяет отделить движение наблюдателя от движения источника. Для иллюстрации рассмотрим три примера. Спешим успокоить читателя: это кажущееся недоразумение, его разъяснение приведено ниже в конце рассмотрения примера 4. С принципом Галилея всё в порядке. . При сближении с полицейской машиной водитель воспринимает звук частотой
. При сближении с полицейской машиной водитель воспринимает звук частотой



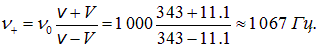
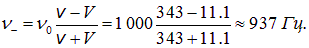



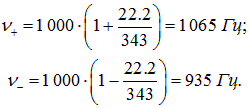
 . Пусть в момент времени t = 0 источник был в точке S0, а в момент t он находится в точке St (рис. 2.23). Расстояние между этими точками равно
. Пусть в момент времени t = 0 источник был в точке S0, а в момент t он находится в точке St (рис. 2.23). Расстояние между этими точками равно  .
.
 источник переместится в точку
источник переместится в точку 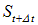 . Соответственно переместится и конус Маха, захватив новые области пространства (показано пунктирной линией).
. Соответственно переместится и конус Маха, захватив новые области пространства (показано пунктирной линией). , пройденного звуковой волной за время t, к расстоянию
, пройденного звуковой волной за время t, к расстоянию  , пройденного источником за то же время:
, пройденного источником за то же время:


 , то есть скорости источника к скорости звука в данной среде.
, то есть скорости источника к скорости звука в данной среде.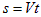 . Так как в этот момент звук достиг наблюдателя, то точка наблюдения оказалась на конусе Маха (рис. 2.24).
. Так как в этот момент звук достиг наблюдателя, то точка наблюдения оказалась на конусе Маха (рис. 2.24).