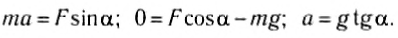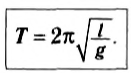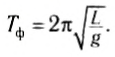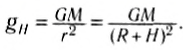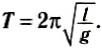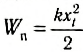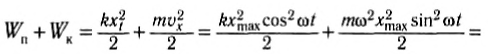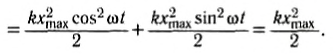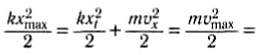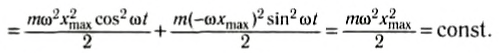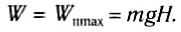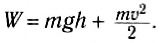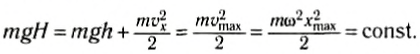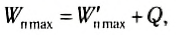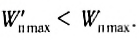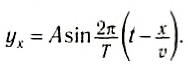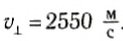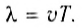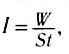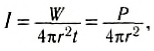Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Колебания и волны уравнение колебаний камертона
- Механические колебания и волны в физике — формулы и определение с примерами
- Механические колебания и волны
- Пружинный и математический маятники
- Превращения энергии при гармонических колебаниях
- Свободные и вынужденные колебания. Резонанс
- Распространение колебаний в упругой среде. Продольные и поперечные волны
- Звук
- Механические и электромагнитные волны
- Возникновение и распространение механических волн
- Как и почему в среде распространяется механическая волна
- Поперечные и продольные механические волны
- Основные свойства волн
- Физические величины, характеризующие колебания
- Длину и скорость распространения волны
- Виды механических колебаний и волн
- Незатухающие и затухающие колебания
- Свободные и вынужденные колебания, автоколебания
- Гармонические колебания
- Справочная информация о колебаниях
- Пружинный маятник
- Математический маятник
- Превращение энергии при механических колебаниях
- Механические волны
- Скорость распространения волны
- Звуковые волны
- Звуковые явления
- 🎬 Видео
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_) ) , единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ) , единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ) , единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Видео:Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ) , единицы времени – с -1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ) , единицы измерения – рад/с.
Видео:Лекция №11 "Колебания" (Булыгин В.С.)Скачать

Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ) , определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Видео:🔴 ОГЭ-2022 по физике. Урок №21. Механические колебания и волныСкачать

Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Видео:🔴 Курс ОГЭ-2024 по физике. Урок №26. Механические колебания и волны | Бегунов М.И.Скачать

Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Видео:Механические колебания и все что нужно про них знать. Онлайн школа EXAMhackСкачать

Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ) , единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук ( ( nu ) ( nu ) ( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Видео:Урок 95 (осн). Механические волны. ЗвукСкачать

Колебания и волны уравнение колебаний камертона
Учебник Физика 7 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 страниц вышел из печати в июле 2015 г. в пятом издании. Учебник физики 7 класса рассчитан на 2 урока в неделю и содержит 6 тем курса физики, которые перечислены ниже.

Физика. Физическая величина. Измерение физических величин.
Цена делений шкалы прибора. Погрешность прямых и косвенных измерений.
Формулы и вычисления по ним. Единицы физических величин.
Метод построения графика.

Явление тяготения и масса тела. Свойство инертности и масса тела.
Плотность вещества. Таблицы плотностей некоторых веществ.
Средняя плотность тел и их плавание.
Метод научного познания.

Сила и динамометр. Виды сил.
Уравновешенные силы и равнодействующая.
Сила тяжести и вес тела. Сила упругости и сила трения.
Закон Архимеда. Вычисление силы Архимеда.
Простые механизмы. Правило равновесия рычага.

Определение давления. Давление жидкости. Закон Паскаля. Давление газа.
Атмосферное давление. Барометр Торричелли. Барометр-анероид.
Вакуумметры. Манометры: жидкостные и деформационные.
Пневматические и гидравлические механизмы.

Механическая работа. Коэффициент полезного действия. Мощность.
Энергия. Кинетическая и потенциальная энергия.
Механическая энергия. Внутренняя энергия.
Взаимные превращения энергии.

Температура и термометры. Количество теплоты и калориметр.
Теплота плавления/кристаллизации и парообразования/конденсации.
Первый закон термодинамики. Двигатель внутреннего сгорания.
Теплота сгорания топлива и КПД тепловых двигателей.
Теплообмен. Второй закон термодинамики.
 |
Учебник Физика 8 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в четвёртом издании. Учебник физики 8 класса рассчитан на 2 урока в неделю и содержит 5 тем курса физики, которые перечислены ниже.

Из истории МКТ. Частицы вещества. Движение частиц вещества.
Взаимодействие частиц вещества. Систематизирующая роль МКТ.
Кристаллические тела. Аморфные тела. Жидкие тела. Газообразные тела.
Агрегатные превращения. Насыщенный пар. Влажность воздуха.

Строение атомов и ионов. Электризация тел и заряд.
Объяснение электризации. Закон сохранения электрического заряда.
Электрическое поле. Электрический конденсатор. Электрический ток.
Электропроводность жидкостей, газов и полупроводников.

Электрическая цепь. Сила тока. Электрическое напряжение. Работа тока.
Закон Ома для участка цепи. Сопротивление соединений проводников.
Закон Джоуля-Ленца. Электронагревательные приборы.
Полупроводниковые приборы. Переменный ток.

Магнитное поле. Соленоид и электромагнит. Постоянные магниты.
Действие магнитного поля на ток. Электродвигатель на постоянном токе.
Электромагнитная индукция. Электротрансформатор. Передача электроэнергии.
Электродвигатель на переменном токе.

Период, частота и амплитуда колебаний. Нитяной и пружинный маятники.
Механические волны. Свойства механических волн. Звук.
Электромагнитные колебания. Излучение и прием электромагнитных волн.
Свойства электромагнитных волн. Принципы радиосвязи и телевидения.
 |
Учебник Физика 9 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в третьем издании. Учебник физики 9 класса рассчитан на 2 урока в неделю и содержит 4 темы курса физики, которые перечислены ниже.

Что такое кинематика. Относительность движения. Путь и перемещение.
Сложение и вычитание векторов. Проекции векторов на координатные оси.
Равномерное движение. Мгновенная скорость. Равноускоренное движение.
Графическое описание движений. Равномерное движение по окружности.

Что такое динамика. Первый, второй и третий законы Ньютона.
Законы Гука и Кулона-Амонтона. Закон всемирного тяготения.
Закон сохранения импульса. Реактивное движение.
Кинетическая энергия. Потенциальная энергия.

Источники света. Прямолинейное распространение света. Отражение света.
Зеркала. Преломление света. Линзы. Оптические приборы.
Дисперсия света и цвета тел. Фотография и полиграфия.
Корпускулярно-волновой дуализм.

Физика XX века. Явление радиоактивности. Регистрация частиц.
Строение атома. Характеристики атомного ядра. Ядерные реакции.
Природа и свойства радиоактивных излучений. Энергия связи ядра.
Энергия ядерных реакций. Ядерная энергетика. Физика XXI века.
Для перехода к параграфам кликайте нумерацию 01 02 03 04 05 и т.д. вверху страницы. Параграфы каждой темы курса физики снабжены интерактивными вопросами и заданиями.
| Физические величины, характеризующие колебания | |||
Частота колебаний 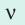 | Период колебаний 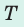 | Амплитуда колебаний 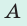 | |
| Определение | количество колебаний за единицу времени | время одного колебания | максимальное расстояние, на которое отклоняется точка от положения равновесия |
| Формула для определения |  | ||
| Единица в СИ | метр (м) | ||
Обратите внимание! При распространении механической волны все части среды, в которой распространяется волна, колеблются с одинаковой частотой 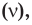
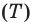
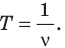
Длину и скорость распространения волны
Вспомните распространение волны вдоль веревки. Пусть конец веревки осуществил одно полное колебание, то есть время распространения волны равно одному периоду 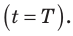
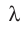
Рис. 17.8. Длина волны равна расстоянию, на которое распространяется волна за время одного колебания (это также расстояние между двумя ближайшими гребнями или двумя ближайшими впадинами)
Длина волны 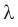
где 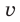
Единица длины волны в СИ — метр:
Нетрудно заметить, что точки веревки, расположенные друг от друга на расстоянии одной длины волны, колеблются синхронно — имеют одинаковую фазу колебаний (рис. 17.8, б, в). Например, точки А и В веревки одновременно движутся вверх, одновременно достигают гребня волны, затем одновременно начинают двигаться вниз и т. д.
Воспользовавшись формулой 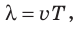
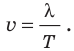
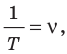
Если волна переходит из одной среды в другую, скорость ее распространения изменяется, а частота остается неизменной, поскольку частота определяется источником волны. Таким образом, согласно формуле 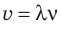
Формула волны
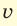
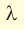
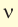
Пример №8
Поперечная волна распространяется вдоль шнура со скоростью 3 м/с. На рис. 1 показано положение шнура в некоторый момент времени и направление распространения волны. Считая, что сторона клетки равна 15 см, определите:
1) амплитуду, период, частоту и длину волны;
2) направление, в котором в данный момент времени движутся точки К, В и С шнура.
Анализ физической проблемы, решение
Волна поперечная, поэтому точки шнура колеблются перпендикулярно направлению распространения волны (смещаются вниз-вверх относительно некоторых положений равновесия).
1) Из рис. 1 видим, что максимальное отклонение от положения равновесия (амплитуда А волны) равно 2 клеткам. Значит,
Расстояние между гребнем и впадиной — 60 см (4 клетки), соответственно расстояние между двумя ближайшими гребнями (длина волны) вдвое больше. Значит,
Частоту 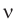
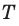
2) Чтобы выяснить направление движения точек шнура, выполним дополнительное построение. Пусть за небольшой интервал времени 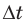
Волна поперечная, то есть точки шнура движутся перпендикулярно направлению распространения волны. Из рис. 2 видим, что точка К через интервал времени 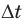
Ответ: 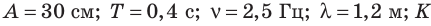
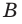
Подводим итоги:
Распространение колебаний в упругой среде называют механической волной. Механическую волну, в которой части среды колеблются перпендикулярно направлению распространения волны, называют поперечной; волну, в которой части среды колеблются вдоль направления распространения волны, называют продольной.
Волна распространяется в пространстве не мгновенно, а с некоторой скоростью. При распространении волны происходит перенос энергии без переноса вещества. Расстояние, на которое распространяется волна за время, равное периоду, называют длиной волны — это расстояние между двумя ближайшими точками, которые колеблются синхронно (имеют одинаковую фазу колебаний). Длина 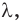
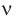
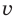
Видео:механические колебания и волныСкачать

Виды механических колебаний и волн
Механические колебания окружают нас повсюду: покачивание ветвей деревьев, вибрация струн музыкальных инструментов, колебания поплавка на волне, движение маятника в часах, биение сердца и т. д. Колебательное движение, одно из самых распространенных в природе.
Механические колебания — это движения тела (или системы тел), происходящие около некоторого положения равновесия и точно или приблизительно повторяющиеся через равные интервалы времени.
Колебательное движение, как и любое другое движение, характеризуется такими физическими величинами, как скорость, ускорение, координата (смещение).
Смещение x — это расстояние от положения равновесия до точки, в которой в данный момент времени находится колеблющееся тело.
При колебаниях механическое состояние тела непрерывно изменяется. Если координата и скорость движения тела повторяются через равные интервалы времени, такие колебания называют периодическими. Существует ряд физических величин, характеризующих именно периодические колебания, в частности амплитуда, период, частота (см. рис. 19.1, таблицу).
Физические величины, характеризующие периодические колебания
Рис. 19.1. Груз на пружине совершает периодические колебания (x — смещение груза; A — амплитуда колебаний). Интервал времени, за который груз переместился из положения 1 в положение 2 и обратно (время одного колебания), — период колебаний T
Незатухающие и затухающие колебания
Рассмотрим колебания груза на пружине (рис. 19.1). Если бы в системе «груз — пружина — Земля» не было потерь механической энергии, то колебания продолжались бы сколь угодно долго, а их амплитуда со временем не изменялась бы. Колебания, амплитуда которых со временем не изменяется, называют незатухающими.
Однако в любой системе всегда есть потери механической энергии. Энергия расходуется на преодоление сил трения, на деформацию тел во время колебаний. В результате механическая энергия постепенно переходит во внутреннюю. Поэтому, если система не получает энергию извне, то амплитуда колебаний постепенно уменьшается и спустя некоторое время колебания прекращаются (затухают). Колебания, амплитуда которых со временем уменьшается, называют затухающими.
Свободные и вынужденные колебания, автоколебания
Существуют колебания, которые происходят без внешнего периодического воздействия. Таковы, например, колебания подвешенного на нити или на пружине шара, возникающие после того, как шар отклонили от положения равновесия и отпустили. Такие колебания называют свободными.
Свободные колебания — это колебания, происходящие под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Частота свободных колебаний определяется свойствами самой системы.
Рис. 19.2. Чтобы в колебательной системе возникли свободные колебания, необходимо вывести ее из положения равновесия — сообщить потенциальную (а) или кинетическую (б) энергию
Систему тел, в которой могут возникать свободные колебания, называют колебательной системой. Характерная черта колебательной системы — наличие положения устойчивого равновесия, около которого и происходят свободные колебания. Чтобы в колебательной системе возникли свободные колебания, необходимо выполнение двух условий:
- системе должна быть передана избыточная энергия (рис. 19.2);
- трение в системе должно быть достаточно мало, иначе колебания быстро затухнут или даже не возникнут.
При свободных колебаниях система не получает энергию извне, поэтому свободные колебания — это всегда затухающие колебания. Чем больше трение в системе, тем быстрее затухают колебания. Например, в воздухе колебания тела на пружине длятся достаточно долго, а в воде быстро затухают (на этом явлении основана работа гидравлических амортизаторов автомобилей (рис. 19.3)).
Рис. 19.3. С кузовом автомобиля соединяют поршень, который во время колебаний движется в цилиндре, заполненном жидкостью; значительное сопротивление жидкости приводит к затуханию колебаний
Существуют колебания (движение воздуха в духовых инструментах, поршня — в двигателе внутреннего сгорания и т. д.), которые совершаются, только когда на тело действуют периодически изменяющиеся внешние силы. Такие колебания называют вынужденными.
Вынужденные колебания — это колебания, происходящие в системе в результате действия внешней периодически изменяющейся силы.
Вынужденные колебания — это обычно незатухающие колебания, частота которых равна частоте изменения внешней силы, вынуждающей тело колебаться.
Есть системы, в которых незатухающие колебания существуют не благодаря периодическому внешнему воздействию, а в результате способности таких систем самим регулировать поступление энергии от постоянного (не периодического) источника. Такие системы называют автоколебательными, а незатухающие колебания в таких системах — автоколебаниями.
Незатухающие колебания, происходящие в системе за счет поступления энергии от постоянного источника, которое регулируется самой системой, называют автоколебаниями.
Частота автоколебаний, как и частота свободных колебаний, определяется свойствами самой системы. Примером механической автоколебательной системы может быть храповый механизм маятниковых часов (рис. 19.5).
Рис. 19.5. Когда маятник 1 приближается к крайнему левому положению, палета b цепляется за зуб храпового колеса 3 и маятник получает толчок влево, приобретая дополнительную энергию
Практически в любой автоколебательной системе можно выделить три характерных элемента: колебательную систему, в которой могут происходить свободные колебания (в нашем примере это маятник 1 часов), источник энергии (поднятая гиря 2, которая поворачивает храповое колесо 3), устройство обратной связи, регулирующее поступление энергии от источника определенными порциями (анкер 4, посредством которого маятник «руководит», в какой момент гиря передает энергию храповому колесу).
Гармонические колебания
По характеру зависимости смещения (координаты) x тела от времени t его колебаний различают гармонические и негармонические колебания. Как правило, зависимость x (t) достаточно сложная (рис. 19.6). Рассмотрим график колебаний тела на пружине (рис. 19.6, в).
Кривая, изображенная на графике, — косинусоида. Колебания, при которых координата x колеблющегося тела изменяется с течением времени t по закону косинуса (или синуса), называют гармоническими колебаниями:
Данные уравнения называют уравнениями гармонических колебаний. Выясним, что означает в этих уравнениях каждая величина.
Обратите внимание! Если координата тела изменяется по гармоническому закону (по закону косинуса или синуса), скорость и ускорение движения тела тоже изменяются гармонически. При этом выполняются соотношения:
И наоборот: если в любой момент времени движения тела его ускорение прямо пропорционально смещению и направлено в сторону, противоположную смещению, то такое движение представляет собой гармонические колебания.
- Если начало отсчета времени (t = 0) совпадает с моментом максимального отклонения тела от положения равновесия (
), то уравнение колебаний удобнее записывать в виде:
(рис. 19.7, а).
- Если начало отсчета времени (t = 0) совпадает с моментом прохождения телом положения равновесия
то уравнение колебаний удобнее записывать в виде: x = Asinωt (рис. 19.7, б).
- По графику колебаний (как и по уравнению колебаний) легко определить физические величины, характеризующие колебательное движение.
Видео:решение задач по теме механические колебания и волны 9 классСкачать

Рис. 19.7. Графики гармонических колебаний (A — амплитуда колебаний; Т — период колебаний). Координата колеблющегося тела изменяется в зависимости от времени t по закону: x = Acosωt (а); x = Asinωt (б)
По графику определите амплитуду и период колебаний тела. Вычислите циклическую частоту и максимальную скорость движения тела. Запишите уравнение колебаний. Найдите смещение тела в фазе 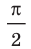
Решение:
График колебаний — синусоида, поэтому уравнение колебаний имеет вид: x = Аsinωt . Из графика видим: максимальное смещение тела равно 5 см: 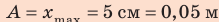
Подставим значения 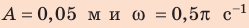
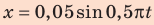
Если
- Движения, точно или приблизительно повторяющиеся через одинаковые интервалы времени, называют механическими колебаниями.
- Колебания, амплитуда которых со временем не изменяется, называют незатухающими; колебания, амплитуда которых со временем уменьшается, — затухающими.
- Колебания, происходящие в системе в результате действия периодически изменяющейся внешней силы, называют вынужденными, а происходящие под действием только внутренних сил системы, — свободными.
- Незатухающие колебания, происходящие в системе за счет поступления энергии от постоянного (не периодического) источника, которое регулируется самой системой, называют автоколебаниями.
- Колебания, в процессе которых смещение x колеблющегося тела изменяется с течением времени t по закону косинуса (или синуса), называют гармоническими. В общем случае уравнение гармонических колебаний имеет вид:
, где A — амплитуда колебаний;
— фаза колебаний
— начальная фаза; ω — циклическая частота.
Справочная информация о колебаниях
Колебанием называется процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около некоторого своего среднего значения.
Например, на качелях, подвешенных на веревках, человек отклоняется то вперед и вверх, то назад и вверх от положения равновесия.
Механической колебательной системой называется совокупность тел, в которой могут происходить колебательные процессы. На рисунке 196 представлены наиболее простые механические колебательные системы: вертикальный пружинный маятник (рис. 196, а) образуют Земля, штатив, пружина и груз; физический маятник (рис. 196, б) — Земля, штатив и шарик на нити; горизонтальный пружинный маятник (рис. 196, в) — два штатива, две пружины и шарик.
Для возникновения колебаний в любой из этих систем необходимо вывести подвешенное тело из положения устойчивого равновесия.
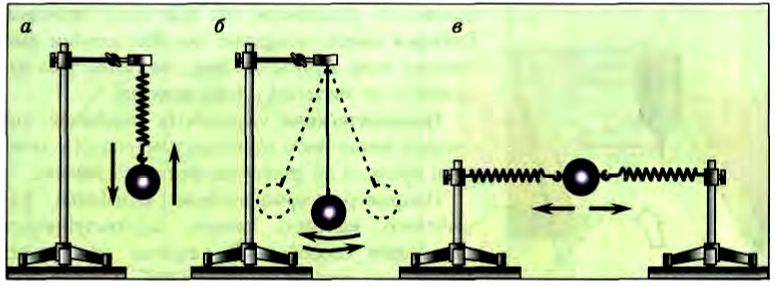
Рис. 196
Всякая колебательная система имеет положение устойчивого равновесия и самопроизвольно (без внешнего воздействия) из него выйти не может.
Периодическими называются колебания, повторяющиеся через определенный промежуток времени.
Периодом колебания называется промежуток времени, в течение которого совершается одно полное колебание. Если за промежуток времени t совершено N полных колебаний, то период определяется по формуле:
Частота колебаний, как и при вращательном движении, — величина, обратная периоду, равная числу колебаний, совершенных системой за одну секунду:
В СИ период измеряется в секундах (с), а частота — в герцах (Гц).
Смещением называется любое отклонение физической величины от ее значения в положении равновесия.
Амплитудой А называется максимальное смещение. На рисунке 197 показан горизонтальный пружинный маятник, состоящий из тела, которое может двигаться по гладкому столу (без трения) около положения равновесия под действием пружины. Выберем начало координат под положением равновесия тела. В этой системе смещение тела изменяется от значения -А до значения А. 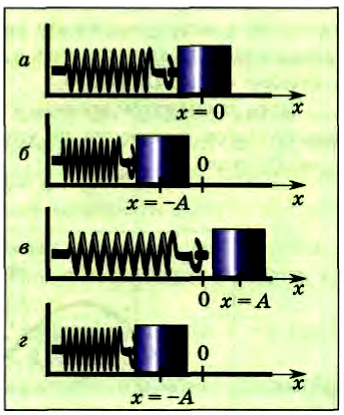
Рис. 197
Гармоническими называются колебания, при которых какая-либо величина изменяется с течением времени по закону синуса или косинуса.
Например, гармонические колебания физического маятника можно зарегистрировать следующим способом. В качестве груза взять небольшой флакон с чернилами, которые могут вытекать через очень маленькое отверстие снизу. Под колеблющимся маятником двигать равномерно по столу бумажную ленту (рис. 198).
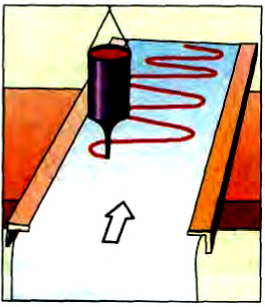
Рис. 198
Полученная на бумаге кривая (рис. 199) называется осциллограммой (лат. oscillum — колебание, греч. graphic — пишу) и представляет собой синусоиду или косинусоиду в зависимости от выбора начального момента времени наблюдения (момента отсчета времени).
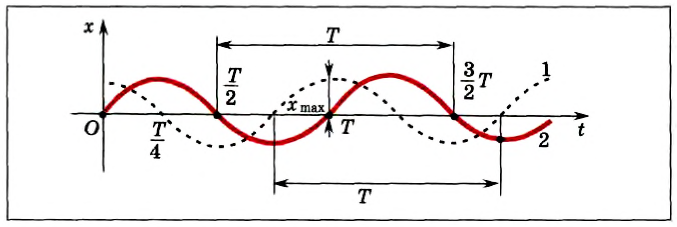
Рис. 199
Чтобы установить основные кинематические признаки гармонических колебаний, рассмотрим их математическую модель на примере изменения физических величин, характеризующих движение маленького шарика (материальной точки) по окружности с постоянной угловой скоростью ω. Начало координат поместим в центре окружности радиуса R. Пусть в начальный момент времени материальная точка находилась в положении M0 (рис. 200) и ее радиус-вектор составлял с осью Ox угол φ0.
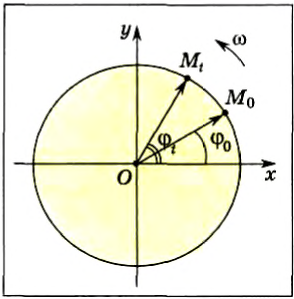
Рис. 200
Через промежуток времени t точка переместилась в положение M1, а ее радиус-вектор повернулся на угол ∆φ = ωt и составляет в данный момент с осью Ox угол
φ1 =φ0 +Δφ = φ0+ωt.
Тогда в момент времени / координаты точки: 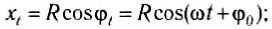
Расположим перпендикулярно плоскости картона и перпендикулярно друг другу два экрана и будем освещать движущийся шарик (рис. 201). На вертикальном экране 1 тень от шарика будет двигаться вдоль оси Oy по закону yl =Rsinφt = Psin(ωt + φ0), т. е. совершать колебания возле начала координат. На горизонтальном экране тень шарика будет двигаться вдоль оси Ox по закону xl =Rcosφt = Pcos(ωt + φ0), и также совершать колебания около начала координат.
Рис. 201
Фазой колебания называется аргумент синуса или косинуса, или, в выбранной системе отсчета, угол между радиус-вектором и осью Ох. Так как sinφt = cos(90 o -φt), то говорят, что колебания координаты xt сдвинуты по фазе на 90° или на 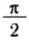
Начальная фаза колебания φ0 характеризует положение точки в начальный момент времени. Если в начальный момент времени шарик находится на оси Ох, то начальная фаза колебания равна нулю.
Так как -1 ≤sinφt≤ 1 и -1 ≤cosφt≤ 1, координаты шарика и его теней изменяются в пределах: -R ≤ xt ≤ R, -R ≤ yt ≤ R.
Таким образом, мгновенные значения координат хt и yt можно рассматривать как смещения от нулевого значения, а модуль амплитудного значения для обеих координат равен радиусу окружности: |xmax| = |mmax| = R.
Так как шарик движется с постоянной угловой скоростью ω, то модули его линейной скорости и центростремительного ускорения постоянны и равны υ = ωR, a = ω 2 R. Но направление каждого из этих векторов меняется с течением времени, и поэтому изменяются их проекции на оси координат.
Выразим проекции вектора скорости через ее модуль и угол поворота радиус-вектора (рис. 202, а): 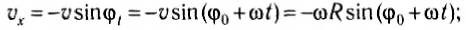
Для проекций ускорения на оси координат (рис. 202, б):
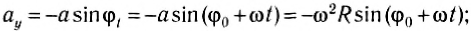
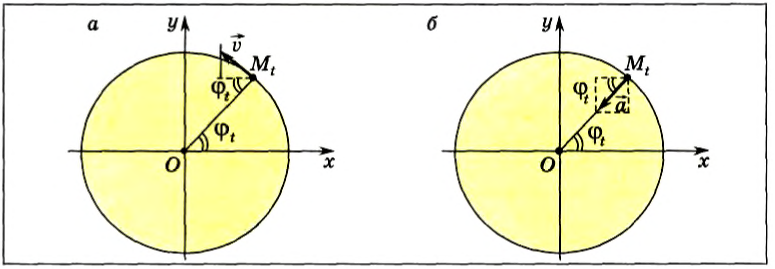
Рис. 202
Из этих уравнений следует, что проекции векторов скорости и ускорения также зависят от времени по гармоническому закону. Модули амплитудных значений проекций скорости равны:
а модули амплитудных значений проекций ускорения равны:
Следовательно, колебательное движение является сложным переменным движением, так как и скорость и ускорение точки зависят от времени.
Для упрощения примем, что в начальный момент движения точка находилась на оси Ох, т. е. φ0 = 0 и φt = ωt.
На рисунке 203 представлена зависимость координаты х (кривая 1) и проекции ускорения ах (кривая 2) на ось Ox от времени:
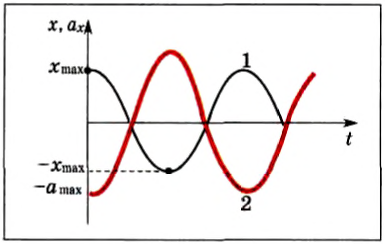
Рис. 203
На рисунке 204 представлена зависимость координаты у (кривая 1) и проекции ускорения ay( кривая 2) на ось Oy от времени:
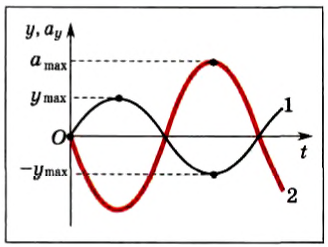
Рис. 204
Сравнение графиков каждой координаты с соответствующим графиком ускорения показывает: 1) графики проекций ускорений сдвинуты относительно графиков координат на 180 o = π, или, как говорят, проекция ускорения изменяется с течением времени в противофазе изменению координаты; 2) в любой момент времени проекция ускорения пропорциональна координате (смещению): αy = -ω 2 yt, ax=-ω 2 xt, с коэффициентом пропорциональности ω 2 . Знак «-» соответствует противоположному отклонению проекций ускорения и координат от нулевых значений в любой момент времени.
Соотношения αy = -ω 2 yt, ax=-ω 2 xt являются основным признаком гармонических колебаний, так как справедливы только для гармонически изменяющихся с течением времени величин.
При гармонических колебаниях ускорение направлено к положению равновесия, противоположно по фазе смещению, а модуль ускорения пропорционален модулю смещения с коэффициентом пропорциональности ω 2 .
Физическая величина ω называется циклической частотой гармонических
колебаний: 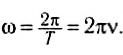
Циклическая частота измеряется в радианах в секунду (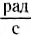
Необходимо отметить, что если при рассмотрении какого-нибудь колебательного процесса получено соотношение, подобное ax =-ω2xt, то можно считать этот процесс зависящим от времени по гармоническому закону. Тогда по формуле 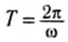
Главные выводы:
- При колебательном движении физическая величина изменяется только в определенном интервале значений, отклоняясь от равновесного значения то в одну сторону, то в другую.
- При гармонических колебаниях координата, проекция скорости и проекция ускорения точки изменяются с течением времени по гармоническому закону.
- Основным признаком колебательного процесса, зависящего от времени по гармоническому закону, является соотношение между проекцией ускорения и смещением: ax=-ω 2 xt.
Пружинный маятник
Пружинным маятником называется система, состоящая из пружины жесткостью k и тела массой m. В простейшей модели пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают: 1) сопротивлением среды и трением скольжения; 2) размерами тела. т. е. тело считается материальной точкой, хотя чаще всего его изображают прямоугольником; 3) массой пружины.
- Горизонтальный пружинный маятник — маятник, в котором колебания тела на пружине происходят вдоль горизонтальной прямой.
- Вертикальный пружинный маятник — маятник, в котором колебания тела на пружине происходят вдоль вертикальной прямой.
Рассмотрим колебания горизонтального пружинного маятника. Пусть пружина прикреплена к вертикальной стене, а тело может скользить без трения по гладкому горизонтальному столу (рис. 207, а).
Если пружина не растянута, то на покоящееся тело действуют только сила тяжести 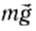
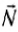
Выведем тело из положения равновесия, растягивая при этом пружину, и отпустим его. Так как пружина растянута, то на тело действует сила упругости пружины 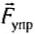
В системе координат, начало которой расположено под положением равновесия тела (рис. 207, б), запишем для проекций на ось Оу: 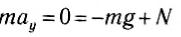
и ось Ох:
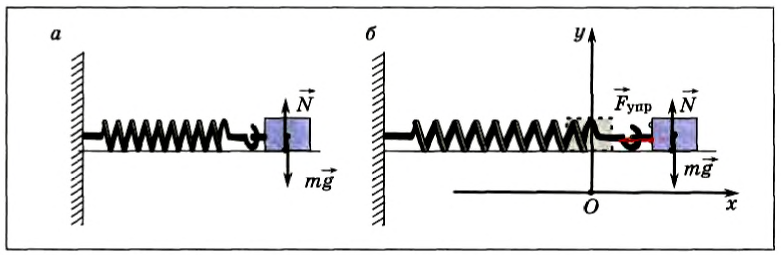
Рис. 207
Согласно закону Гука проекция силы упругости в выбранной системе отсчета: 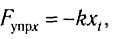
где xt — абсолютное удлинение пружины, или координата тела в выбранной системе отсчета.
Выразим проекцию ускорения: 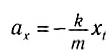
и сравним с соотношением, характеризующим гармонические колебания:
Сравнение позволяет считать, что 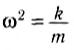
и циклическая частота колебаний равна:
а период колебаний тела на пружине:
Чтобы записать уравнение гармонических колебаний для координаты тела, необходимо знать амплитуду и фазу колебаний.
Амплитуда колебаний xmax равна максимальному значению координаты тела, или максимальному абсолютному удлинению пружины. Эта величина в соответствии с законом Гука: Fупрmax =-kxmax и третьим законом Ньютона: 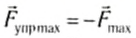
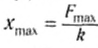
Пусть в начальный момент времени координата тела максимальна, т. е. мы начинаем следить за его движением в момент начала движения тела к положению равновесия. Тогда уравнение для координаты может быть записано как: 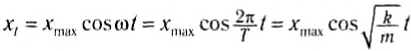
с начальной фазой φ0 = 0.
Или по закону синуса:
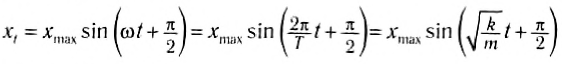
с начальной фазой
В соответствии с формулами, полученными при рассмотрении гармонических колебаний, можно записать уравнения для проекций скорости и ускорения тела:
где модули максимальных (амплитудных) значений скорости и ускорения соответственно равны:
Рассмотрим характеристики движения тела в некоторые моменты времени.
Через промежуток времени, равный 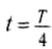
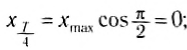
В этот момент тело проходит положение равновесия (рис. 208, а) с максимальной скоростью, а ускорение равно нулю, так как пружина не деформирована.
Через половину периода 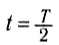
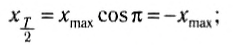
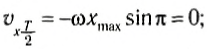
В этот момент тело на мгновение останавливается, пружина максимально сжата, и, соответственно, ускорение максимально и направлено к положению равновесия (рис. 208, б).
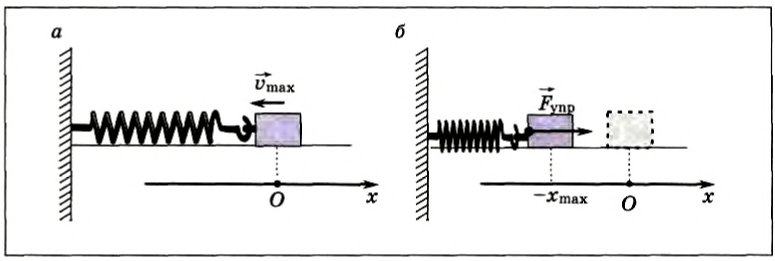
Рис. 208
Через промежуток времени, равный периоду, координата тела равна
: 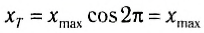
В таком идеальном случае, без действия сил трения и сопротивления, тело на пружине должно колебаться бесконечно долго.
Колебания называются незатухающими, если их амплитуда постоянна, т. е. не зависит от времени. Следовательно, рассмотренные колебания пружинного маятника являются незатухающими.
Можно показать, что для вертикального пружинного маятника циклическая частота или период колебаний определяются теми же величинами k и m и равны:
Жесткость пружины и масса груза — характеристики данной колебательной системы, а колебания поддерживаются за счет силы упругости, которая является силой взаимодействия между телом и пружиной в колебательной системе.
Свободными, или собственными, называются колебания, происходящие только под действием сил взаимодействия в самой колебательной системе при отсутствии сил сопротивления движению.
Период или частота собственных (свободных) колебаний обусловлены только характеристиками колебательной системы, а амплитуда колебаний остается неизменной и определена причинами, которые вывели систему из положения равновесия.
Главные выводы:
- Пружинный маятник — модель колебательной системы, в которой рассматривают только упругую деформацию пружины и пренебрегают массой пружины и размерами тела.
- Колебания пружинного маятника являются гармоническими, форма записи уравнения колебаний (косинусоидальные или синусоидальные) выбирается в зависимости от начальных условий и удобства математической записи.
, амплитуда колебаний определяется причинами, которые вывели маятник из положения равновесия.
- Период или частота колебаний пружинного маятника зависят только от жесткости пружины и массы тела:
Математический маятник
Рассмотрим колебания маленького стального шарика, подвешенного на длинной нерастяжимой нити. Отклоним нить с шариком на небольшой угол от вертикали и отпустим. Под действием силы тяжести и силы натяжения нити шарик начнет колебательное движение (рис. 209. а). Можно засечь время, например 5 полных колебаний, и определить период колебании.
Из-за сил трения о воздух и внутреннего трения в материале нити возле точки подвеса энергия, полученная шариком при выведении из положения равновесия, постепенно переходит во внутреннюю, и его амплитуда колебаний уменьшается. Измерим вновь время 5 полных колебаний и определим период при меньшей амплитуде. Период колебаний не изменился.
Исследуем, от чего зависит период колебаний. Подвесим на той же нити вместо стального шарика пластмассовый таких же размеров, но меньшей массы. Период колебаний остался прежним.
Если подвесить шарик на нити большей длины, то период колебаний увеличится.
Чтобы получить формулу для периода колебаний, необходимо, как всегда, для упрощения математических расчетов сначала охарактеризовать используемую модель колебательной системы.
Математическим маятником называется находящаяся в гравитационном поле материальная точка, подвешенная на невесомой и нерастяжимой нити.
Математический маятник — это модель малых реальных колебаний тела под действием силы тяготения при условии, что можно пренебречь: I) размерами подвешенного тела по сравнению с длиной нити; 2) сопротивлением движению тела; 3) массой нити; 4) деформацией нити.
Для того чтобы получить формулу для периода колебаний, проведем еще два опыта. Отклоним шарик на нити длиной l на небольшое расстояние от вертикальной линии OO1 и измерим это расстояние R (см. рис. 209, а). Отпустим шарик и определим период его колебаний Tk. Вновь отведем шарик на расстояние R от линии OOt и толкнем так, чтобы шарик начал двигаться по окружности радиуса R, а нить при его движении описывала коническую поверхность (рис. 209, б). Определим период вращения шарика Tв и сравним с периодом колебаний. Эти величины оказываются равными: Тк = Тв. 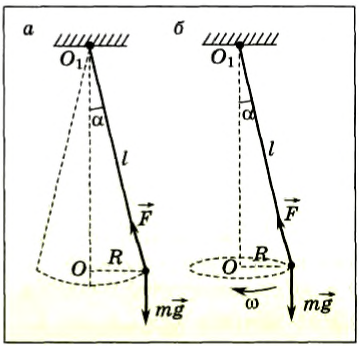
Рис. 209
Шарик движется по окружности с центростремительным ускорением под действием двух сил: силы тяжести 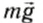
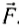
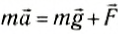
Спроецируем на оси координат и получим выражение для ускорения шарика:
При малых углах отклонения нити 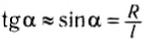
C другой стороны, центростремительное ускорение равно: 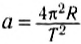
Период колебаний математического маятника можно рассчитать по формуле:
При малых отклонениях от положения равновесия период колебаний математического маятника не зависит от амплитуды. Это свойство маятника называется изохронностью (изо — постоянный, хронос — время).
Свободные колебания математического маятника можно считать гармоническими только при малых углах отклонения нити от вертикали.
Формула для периода свободных (или собственных) колебаний математического маятника показывает, что, как и для пружинного маятника, период колебаний определяется только параметрами колебательной системы: длиной нити и ускорением свободного падения (характеризующим взаимодействие маятника с Землей) в месте расположения маятника.
Так как период колебаний маятника может быть определен и по формуле 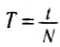
Как мы уже обсуждали, ускорение свободного падения зависит от многих параметров, в том числе и от средней плотности залегающих под почвой пород.
В 30-е годы XX в. не существовало современных физических методов геологической разведки, и контуры знаменитого месторождения магнитного железняка в России «Курская магнитная аномалия» были определены с помощью прибора, основной частью которого был маятник. Там, где плотная железосодержащая порода была близко под почвой, ускорение свободного падения было больше, а период колебаний маятника меньше.
Полученная формула для периода колебаний математического маятника может быть использована для оценки периода колебаний так называемого физического маятника, т. е. колеблющегося тела, размерами которого нельзя пренебречь по сравнению с длиной подвеса. В этом случае используют понятие — приведенная длина Lnp, которая больше L — расстояния от точки подвеса до центра тяжести. Тогда период колебаний физического маятника Γφ можно оценить по формуле:
При использовании маятниковых часов необходимо учитывать зависимость ускорения свободного падения от массы Земли M и расстояния r до ее центра:
Следовательно, при перемещении таких часов высоко в горы, в глубокую шахту или на другую планету период маятниковых часов будет меняться, и они будут отставать или спешить по сравнению с их показаниями в месте изготовления.
Главные выводы
- Математический маятник — это тело малых размеров, подвешенное на длинной невесомой и нерастяжимой нити, совершающее колебания под действием постоянной силы тяготения.
- Колебания математического маятника являются гармоническими лишь при отклонении нити от вертикали на малые углы.
- Период колебаний математического маятника вычисляется по формуле:
Превращение энергии при механических колебаниях
Как мы уже обсуждали, в рассмотренных моделях гармонических колебаний пружинного и математического маятников предполагалось, что сопротивление движению отсутствует.
В этом случае должен выполняться закон сохранения и превращения механической энергии. Покажем выполнение закона сохранения энергии при гармонических колебаниях на примере горизонтального пружинного маятника.
Работа деформирующей силы при растяжении пружины была затрачена на потенциальную энергию упругой деформации: 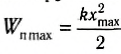
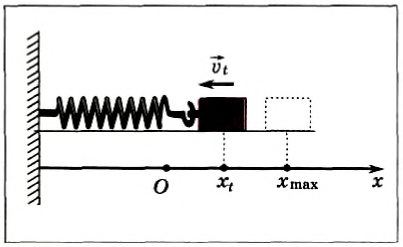
Рис. 210
Двигаясь ускоренно под действием силы упругости, тело приобрело скорость и соответственно кинетическую энергию: 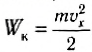
Используя уравнения для координаты и проекции скорости: xt = xmaxcosωt, υx = -xmaxsinωt, и формулу для циклической частоты: 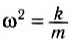
Таким образом, в любой момент времени механическая энергия системы, равная сумме кинетической энергии тела и упругой энергии пружины, остается постоянной и равной начальной максимальной потенциальной энергии.
Полная энергия колебаний может быть выражена и через максимальную кинетическую энергию:
Аналогично можно показать выполнение закона сохранения и превращения механической энергии при свободных колебаниях математического маятника.
В случае возбуждения колебаний при отклонении маятника из положения равновесия работа внешней силы идет на увеличение потенциальной энергии груза маятника. При подъеме на высоту H потенциальная энергия груза относительно положения равновесия (рис. 211):

Рис. 211
При движении маятника к положению равновесия происходит увеличение кинетической энергии
груза за счет потенциальной энергии, и на высоте h полная энергия:
Следовательно, можно записать закон сохранения механической энергии для математического маятника:
Для реального маятника из-за трения о воздух и внутреннего трения в нити возле точки подвеса часть механической энергии за каждый период колебаний переходит во внутреннюю энергию теплового движения атомов и молекул Q.
В этом случае выполняется закон сохранения полной энергии:
и через промежуток времени, равный периоду, максимальное значение потенциальной энергии меньше начального:
Следовательно, в процессе колебательного движения амплитуда колебания уменьшается.
Затухающими называются колебания, амплитуда которых с течением времени уменьшается (рис. 212). Например, если толкнуть качели с сидящим на них человеком, то колебания этой системы будут затухающими. 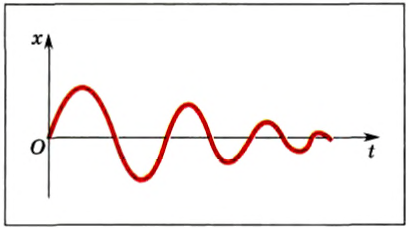
Рис. 212
В этом случае для сохранения амплитуды колебаний необходимо пополнять потери энергии. Например, поддерживать амплитуду колебаний качелей постоянной можно, периодически их подталкивая.
Вынужденными называются колебания, происходящие под действием внешней периодически изменяющейся силы.
Рассмотрим вынужденные колебания в следующем опыте. Подвесим пружинный маятник к стержню с изгибом (рис. 213). который можно вращать е помощью рукоятки. Отверстие, через которое проходит подвес маятника, позволяет ему двигаться только вверх или вниз. При вращении рукоятки с постоянной частотой на маятник будет с такой же частотой действовать сила со стороны стержня.
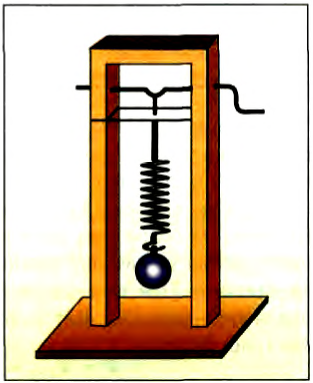
Рис. 213
У пружинного маятника есть собственная частота колебаний. Пусть частота вращения стержня не равна этой частоте. Тогда под действием периодически изменяющейся силы амплитуда колебаний груза сначала увеличивается (рис. 214), а через некоторое время устанавливаются колебания с постоянной амплитудой и периодом, равным периоду вынуждающей силы.
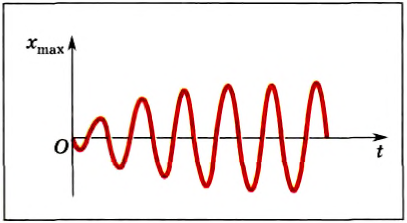
рис. 214
При установившихся колебаниях работа внешней силы равна потерям энергии в колебательной системе, а значение установившейся амплитуды определяется: 1) потерями энергии; 2) амплитудой действующей силы; 3) частотой или периодом внешней силы.
Если изменять частоту вращения стержня соответственно, частоту вынуждающей силы, можно зарегистрировать характерную завимостью амплитуды вынужденных колебаний от частоты (рис. 215), которая называется резонансной кривой. При частоте вынуждающей силы. приближающейся к собственной частоте колебаний маятника, амплитдных колебаний растет, а при больших частотах уменьшается. 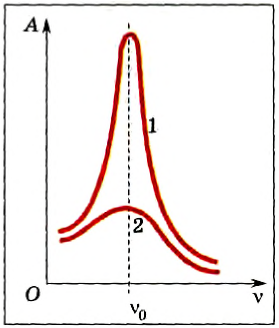
Рис. 215
Механическим резонансом называется резкое возрастание амплитуды возбужденных колебаний, когда частота вынуждающей силы близка к частоте собственных колебаний системы.
Представленные на рисунке 215 резонансные кривые получены при разных силах сопротивления движению. Резонансная кривая 1 получена при силах трения, а резонансная кривая 2 — при наличии больших сил сопративления движению.
Следовательно, резкое возрастание амплитуды вынужденных колебаний в резонансе наблюдается лишь при наличии малых сил сопротивления движению
Например, если толкать качели «в такт» их движению, то можно их «растягивать» до все большей амплитуды. Возрастание амплитуды колебаний происходит до тех пор, пока энергия, поступающая в колебательную систему за работы периодической силы, больше энергии потерь.
Явление резонанса имеет огромное практическое значение, так как используется для усиления различных колебаний в технике.
Вынужденные колебания используют при работе виброустройств для уплотненения сыпучего основания под фундаменты и дороги, уплотнения бетона при заливке фундаментов. Вибраторы применяются для вибрационного забивания свай, труб, при виброукладке бетона, сортировке сыпучих материалов.
Видео:Урок 327. Гармонические колебанияСкачать

Механические волны
Реальные колебательные системы практически всегда расположены в какой-либо среде. Поэтому колебательная система может отдавать энергию частицам среды, непосредственно прилегающим к ней, вызывая их вынужденные колебания. Например, движение качелей происходит в воздухе, и, стоя возле мы ощущаем движение воздуха, как бы ветерок дует на нас при прохожими качелей то с одной, то с другой стороны.
Как мы уже обсуждали, между молекулами вещества существуют силы взаимодействия, которые определяют его упругие свойства. Если какие-то частицы выводятся из положения равновесия, то силы взаимодействия со стороны соседних частиц препятствуют этому и одновременно смещают сами соседние частицы. Вследствие взаимодействия между частицами колебательное движение передается от одной частицы к другой, и колебательный процесс распространяется в среде.
Механической волной называется процесс распространения колебаний в фугой среде.
Как модель возникновения и распространения механической волны можно рассмотреть движение двух поплавков на поверхности воды. Подергаем леску один из них так. чтобы поплавок начал колебаться вверх-вниз, месте с поплавком смещаются соприкасающиеся с ним частицы воды, которые вовлекают в движение ближайшие к ним другие частицы, и от поплавка по всем направлениям распространяются волны. Эти волны вовлекают в колебательное движение второй поплавок, и от него появляются такие же волны.
Важно отметить, что оба поплавка только колеблются возле положения равновесия, а волны распространяются от них во всех направлениях.
Источником колебаний или вибратором называется колеблющееся тело, возбуждающее волновое движение частиц среды.
Рассмотрим модель еще более простой механической волны, которая распространяется только в одном направлении. Для этого возьмем резиновый шнур с нанизанными на него бусинами, один конец закрепим, а второй конец будем периодически двигать вверх-вниз возле положения равновесия (рис. 217). 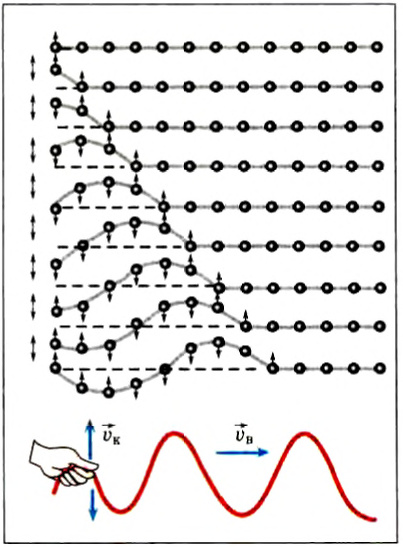
Рис. 217
В качестве источника колебаний выступает наша рука, и пусть ее колебания, а следовательно, колебания ближайшей от нее бусины происходят вдоль оси Oy по закону: 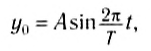
где А — амплитуда колебания бусины, которая подвержена нашим воздействиям, фаза колебания, T — период колебания.
На рисунке показаны положения бусин на шнуре через каждую восьмую часть периода колебаний. В момент 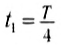
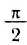
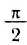
В этом случае говорят, что колебания других бусин отстают по фазе от колебаний первой тем больше, чем дальше они расположены от источника колебаний.
В момент времени 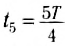
Следовательно, при распространении волны: 1) смещение каждой точки шнура от положения равновесия происходит с течением времени периодически: 2) смещения всех точек шнура в каждый момент времени периодически изменяются от точки к точке, т. е. являются периодической функцией координат.
Иногда говорят, что при распространении волны происходит перемещение фазы колебания от точки к точке с определенной скоростью.
- Фазовой скоростью называется скорость распространения какой-либо фазы от одной точки среды к другой.
- Бегущей волной называется распространение колебательного движения в среде с определенной скоростью υ.
Пусть волна вдоль шнура распространилась до точки с координатой х. Бусина в этой точке будет иметь такую же фазу колебаний, как и первая, но не более поздний момент времени распространения волны, т. е. отставать 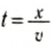
Это уравнение называют уравнением бегущей волны вдоль оси Ох.
Важно понимать, что при распространении бегущей механической волны частицы среды не перемещаются вместе с волной, а только совершают колебания около своих положений устойчивого равновесия. Поэтому бегущая волна не переносит вещество, а переносит энергию колебательного движения.
Словосочетание «колебания частиц совпадают по фазе» используют для ех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции скорости. А фазы колебаний таких частиц отличаются на четное число, умноженное на π: nπ, где n — четное число.
В зависимости от направления колебаний частиц среды относительно направления распространения волны различают поперечные и продольные волны.
Поперечной волной называется распространение колебательного процесса ɪ среде, при котором частицы среды колеблются перпендикулярно направлению распространения волны.
Рассмотренный пример колебаний бусин на шнуре является моделью возникновения и распространения поперечной волны.
Условием распространения поперечных волн в среде является возникновение при деформации сдвига упругих возвращающих сил. Поэтому поперечные волны могут распространяться в твердых веществах, вдоль упругих шнуров, труп и т. д., на поверхности жидкостей.
Продольной волной называется распространение колебательного процесса в среде, при котором частицы среды колеблются вдоль направления распространения волны. Продольные волны возникают при деформации сжатия или растяжения.
Примером продольных волн может служить распространение колебательного процесса вдоль ряда подвешенных шариков, которые скреплены друг с другом одинаковыми пружинками (рис. 218, а). Если вывести из положения равновесия один из шариков и отпустить, то в горизонтальном направлении за счет взаимодействия шариков и пружинок начнет распространяться продольная волна, представляющая собой сгущения и разрежения витков пружин (рис. 218, б). При этом каждый шарик колеблется вдоль направления распространения волны.
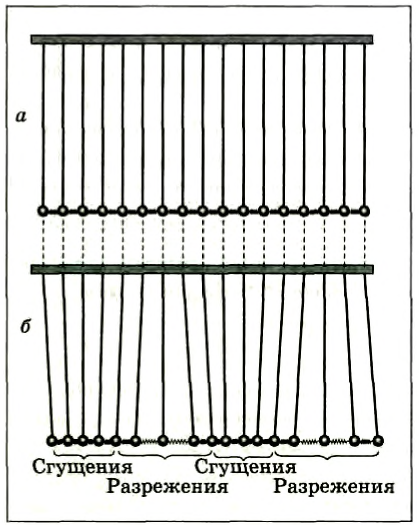
Рис. 218
Продольные волны могут, например, возникать, если в длинной трубке с воздухом возле одного из концов поршень совершает колебательное движение (рис. 219). В этом случае в воздухе будет распространяться упругая волна, представляющая собой чередование сгущений и разрежений среды, которое будет характеризоваться периодическим изменением плотности или давления в среде. Мембрана микрофона, установленного возле другого конца трубки, начнет колебаться под воздействием воздуха, и стрелка присоединенного к микрофону гальванометра также начнет колебаться.
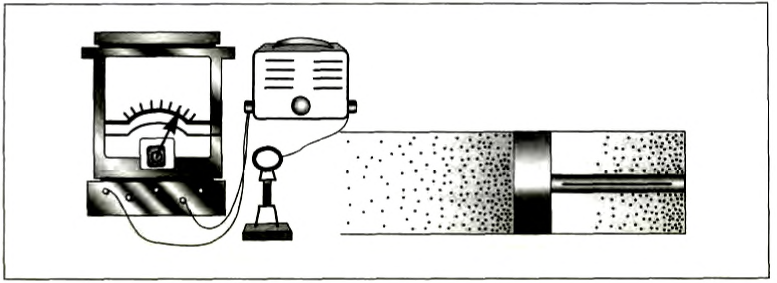
Рис. 219
Продольные волны могут возникать и распространяться в веществе, находящемся в любом состоянии: твердом, жидком и газообразном. Поперечные волны возникают и распространяются только в твердых веществах.
Необходимо отметить, что распространение механических волн определяется передачей энергии колебательного движения от одной частицы к другой. Но частицы среды лишь колеблются возле положений равновесия, а распространяющаяся волна переносит энергию в пространстве. Энергия, переносимая волной, равна сумме кинетических энергий колеблющихся частиц и потенциальной энергии упругой деформации среды.
Главные выводы:
- Механическая волна — это процесс распространения колебаний от одной частицы среды к другой. Период колебаний частиц среды, т, е. период волны, определяется источником колебаний.
- При распространении механической волны частицы среды не перемещаются вместе с волной, а только совершают колебания около своих положений устойчивого равновесия. Поэтому бегущая волна не переносит вещество, а переносит энергию колебательного движения.
- В зависимости от направления колебания частиц среды относительно направления распространения волны различают поперечные и продольные волны.
Скорость распространения волны
Механическая волна — это процесс распространения колебательного движения в среде от частицы к частице, обусловленный взаимодействием между ними. Следовательно, скорость распространения механических волн в среде должна зависеть от сил взаимодействия между частицами среды.
При рассмотрении механических деформаций мы обсуждали, что силы взаимодействия в веществе зависят от свойств молекул или атомов и расстояний, на которых они находятся.
Опыты по изучению механических волн показывают, что скорость их распространения в однородной среде тем больше, чем меньше плотность вещества и чем более упругим оно является.
При изучении простейших упругих деформаций растяжения и сжатия мы познакомились с одной из характеристик упругих свойств вещества — продольным модулем упругости, или модулем Юнга Е.
Установлено, что при распространении продольных волн вдоль стержня их скорость определяется по формуле: 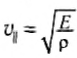
Подобные формулы установлены для скорости распространения продольных и поперечных волн и для более сложных случаев.
Скорость механических волн в среде определяется физическими характеристиками среды: упругими свойствами и плотностью.
Различные виды упругой деформации характеризуются количественно отличающимися коэффициентами. Поэтому, например, в твердых телах продольные волны распространяются быстрее поперечных, и скорость продольных волн в железе 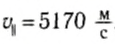
Различия в скорости распространения продольных и поперечных волн в веществе используются для изучения особенностей его строения. Например, в геофизике изучается распространение продольных и поперечных воли в земной коре, что позволяет получать информацию о ее строении и определять расположение эпицентров землетрясений.
Для характеристики волн применяют понятие длина волны, которое можно ввести двумя способами (рис. 222)
- длиной волны λ называется расстояние, на которое распространяется колебательный процесс в среде за время, равное периоду колебаний ее частиц;
- длиной волны λ называется расстояние между двумя ближайшими точками бегущей волны, которые колеблются в одинаковой фазе.
В том, что эти два варианта определения длины волны равноправны, легко убедиться, проанализировав развитие волнового процесса на рисунке 222. 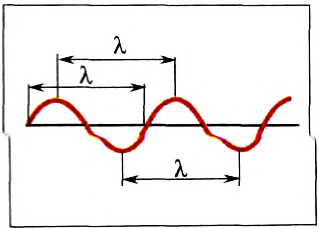
Рис. 222
Пусть известны период T и скорость волны υ. Тогда согласно первому варианту определения ,глины волны:
λ = υT.
Как мы уже обсуждали, период волны определяется источником колебаний, а скорость обусловлена свойствами среды, поэтому при распространении колебательного процесса из одной среды в другую изменяются скорость и длина волны, а частота и период не изменяются.
На границе раздела двух сред может происходить отражение и преломление механических волн, подобное отражению и преломлению света, которое вы рассматривали в оптике.
При этом законы отражения и преломления механических волн аналогичны законам отражения и преломления света.
На практике наблюдаются два типичных случая отражения, один из которых называют отражением с потерей полуволны, а второй — отражением бел потери полуволны.
В случае отражения с потерей полуволны (рис. 223), если волна до отражения двигалась гребнем вперед, то после отражения волна будет распространяться впадиной вперед (и наоборот), т. е. при таком отражении фаза волны изменяется на противоположную. Такое отражение наблюдается на границе двух сред, если скорость распространения волны во второй среде меньше, чем в первой.
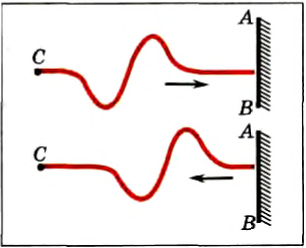
Рис. 223
Если во второй среде скорость распространения волны больше, чем в первой, то от границы этих сред происходит отражение без потери полуволны, т. е. если волна до отражения двигалась гребнем вперед, то и после отражения она будет распространяться гребнем вперед.
Рассмотрим простейшую модель одного из интересных случаев распространения и отражения волн на примере нити, один конец которой привязан к молоточку звонка, а к другому концу через блок подвешена маленькая гирька (рис. 224).
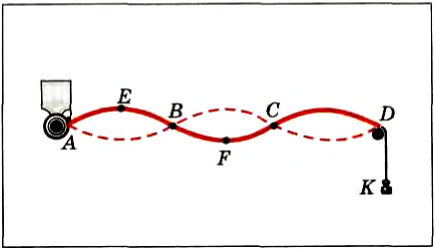
Рис, 224
Частицы нити передают друг другу колебания от молоточка, и волна распространяется до блока, вызывая вынужденные колебания груза. Эти колебания порождают отраженную волну той же частоты. Таким образом, каждая точка нити участвует в двух колебаниях, которые приходят с разных сторон.
Если изменять расстояние от молоточка до блока, то можно наблюдать, как при некоторых расстояниях возникают так называемые стоячие волны.
Стоячие волны возникают только тогда, когда на расстоянии от источника до препятствия, отражающего волны, укладывается целое число четвертей волны.
Название «стоячие волны» возникло потому, что при распространении таких волн нет перемещения фазы между колеблющимися точками, а некоторые из точек стоячей волны совсем не колеблются.
Узлами называются те точки стоячей волны, которые не колеблются. Например, точки А, В, C па рисунке 224. Расстояние между соседними узлами составляет половину длины стоячей волны.
Пучностями называются точки стоячей волны, амплитуды которых максимальны. Например, точки Е, F на рисунке 224.
Стоячие волны можно наблюдать на натянутых горизонтально канатах, струнах. Причем в зависимости от точки воздействия на струну одной и той же длины в ней одновременно могут возникать одна или несколько кратных ей стоячих волн.
В окружающем мире мы часто наблюдаем возникновение и исчезновение (затухание) волн. Например, на спокойной поверхности воды в пруду волны от брошенного камешка довольно быстро исчезают. Или на поверхности лужи при резком порыве ветра вдруг возникает «рябь» — много мелких волн, которые могут исчезнуть так же быстро.
Затуханием волны называется уменьшение ее амплитуды в процессе распространения. Колебательному движению частиц среды препятствуют силы сопротивления. В результате этого энергия колебательного движения частиц переходит во внутреннюю энергию вещества, и волны затухают.
Главные выводы:
- Скорость механических волн зависит от физических характеристик среды: ее упругих свойств и плотности.
- Длиной волны называется расстояние, на которое распространяется колебательный процесс в однородной среде за время, равное периоду колебаний частиц волны (или расстояние между двумя точками волны, колеблющимися в одинаковой фазе).
- При переходе в другую среду период и частота волны остаются постоянными, а скорость распространения волны изменяется, поэтому изменяется и длина волны.
- При различии в скоростях распространения волн в двух средах на их границе происходит отражение и преломление волны.
- Реальное колебательное движение частиц в любой среде происходит при наличии сил сопротивления, и поэтому механические волны в любой реальной среде затухают.
Видео:Механические колебания. Как найти период колебаний? | ЕГЭ 2023 по физикеСкачать

Звуковые волны
Окружающий мир наполнен огромным количеством звуков, которые издают люди, птицы и другие животные, машины и т. д. Что же такое звук и как он возникает?
Проведем опыт с металлической тарелкой из ударных инструментов оркестра (рис. 225). Ударим по краю тарелки, когда она находится на стойке и когда за лежит на мягком кресле.
В обоих случаях мы услышим звуки, но они будут отличаться. Почему звуки разные?

Рис. 225
Тарелка на стойке после удара достаточно долго колеблется, лежащая на кресле — практически не колеблется.
Различные опыты показывают, что звук возникает только от колеблющихся тел, которые называют источниками звука. Каким же образом звук двигает уха человека?
На этот вопрос ответил в 1660 г. английский ученый Р. Бойль. Он изучал звучание колеблющихся тел, помещенных под колокол воздушного насоса (Рис. 226). При наличии под колоколом воздуха звук от звонка хорошо слышны. При откачивании из под колокола воздуха громкость звука уменьшается, и наконец звук совсем исчезает. Если впустить воздух под колокол, то вновь слышен громкий звук. Следовательно, для распространения звука от колеблющегося тела необходима среда.
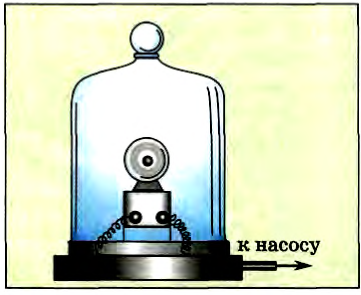
рис. 226
Кроме того, каждый знает, что звуки слышны в воде, через стекло, степы и т. д.
Дело в том, что в окружающем мире: в воздухе, воде, почве, зданиях, мостах. рельсах, автомобилях, мебели и т. д. — непрерывно распространяются разнообразные колебания от различных источников колебаний.
Механические волны в интервале частот приблизительно от 20 Гц до 20 000 Гц слуховая система человека воспринимает как звуковые колебания, а колебания других частот ощущаются нами в основном как вибрация, толчки, удары и т. п.
Акустикой называется раздел физики, изучающий возникновение и распространение звуковых волн.
Большинство звуковых волн достигают уха человека по воздуху, а в газах, как мы обсуждали, распространяются только продольные волны, представляющие собой области сгущения или разрежения молекул, т. е. периодические изменения плотности и давления.
Именно периодические изменения давления воздуха вызывают вынужденные колебания ушной барабанной перепонки, которые сложным образом преобразуются в сигналы, распространяющиеся по нервам в кору головного мозга. Барабанная перепонка и остальная сложная система, определяющая слух человека, способны преобразовывать в нервные импульсы лишь определенный диапазон частот механических колебаний, в среднем от 20 Гц до 20 000 Гц. Поэтому ввели следующие определения.
Звуком называется волновой процесс, распространяющийся в твердых телах в виде продольных и поперечных волн, а в жидкостях и газах в виде продольных волн с частотой в пределах 20—20 000 Гц.
Инфразвуком называются волны с частотой меньше 20 Гц, а ультразвуком — с частотой больше 20 000 Гц. В последнее время при изучении вещества интенсивно используется гиперзвук с частотой порядка 109 Гц.
Частота и период звуковой волны определяются источником звука, т. е. акустическим или звуковым вибратором.
Скорость звуковых волн, как и всех механических волн, зависит от упругих свойств среды и ее плотности. В воздухе, в зависимости от его температуры и влажности, скорость звука 330—340 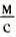
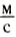
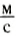
Длину звуковой волны можно вычислить, как и для всех механических волн, по формуле:
Для сравнения звуков используют различные слова, например «высокий» ли «низкий», «металлический» или «музыкальный», при сравнении голосов звонят «бас» или «тенор» и т. д.
Измерения показывают, что звуки, воспринимаемые человеком как «тонне», «высокие», имеют большую частоту, чем звуки «низкие». При этом, как правило, каждое звучащее тело создает свой набор звуковых волн нескольких частот, в результате чего звуки от разных колеблющихся тел отличаются.
Музыкальным тоном называется звуковая волна одной частоты, подчиняющаяся гармоническому закону.
Для настройки музыкальных инструментов используются камертоны рис. 227), каждый из которых сделан так, что создает, практически, звук плюй частоты, или один музыкальный топ.
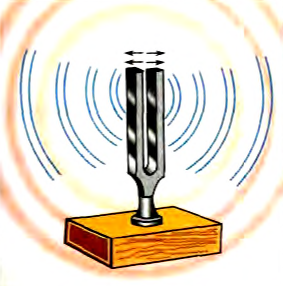
Рис. 227
Для тех, кто занимается музыкой или пением, интересно будет знать, что он «ля» первой октавы (рис. 228) соответствует частоте 440 Гц, тон «ля» второй октавы — частоте 880 Гц и т. д.
Голос, способный издавать звуки низкой частоты, называется, басом. «Нижний» рекорд для баса — звук при частоте 44 Гц. Самая высокая нота, ιpoπeτaπ певицей, соответствовала частоте 2300 Гц.

Рис. 228
Так как большинство звучащих тел создают целый набор звуковых частот, то для описания создаваемых ими звуков принято использовать целый ряд терминов.
Основным тоном называется звук наименьшей частоты, издаваемый звучащим телом.
Обертонами называются звуки более высоких частот, чем основной тон, их частоты являются кратными частоте основного тона.
Тембр сложного звука определяется количеством тонов и их частотами.
Тембр определяет неповторимость звуков человеческих голосов и различных музыкальных инструментов.
В струнах музыкальных инструментов (рис. 229) возникают стоячие волны. Частота стоячей волны зависит от точки воздействия на струну. Поэтому в руках умелого гитариста одна струна может петь, почти как целый оркестр.
Рис. 229
Основной тон голоса человека определяется так называемыми голосовыми связками: чем они тоньше и короче, тем больше частота колебаний и выше голос. Но неповторимость и красоту голоса создают обертоны, которые возникают при колебаниях не только связок, но и губ, языка и т. д.
Чем отличается музыкальный звук от шума?
Шумом называется такой сложный звук, в котором нельзя выделить отдельные гармонические тоны.
Поэтому волчий вой и комариный писк — звуки музыкальные, а барабанный бой и стук кастаньет являются шумом.
А чем отличаются «громкие» и «тихие» звуки?
Громкость звука зависит от энергии колебаний звуковой волны и особенностей слухового аппарата человека.
Самые тихие звуки, воспринимаемые человеком, вызывают колебания барабанной перепонки с энергией порядка 10 -16 Дж. Самые громкие звуки (еще без болевых ощущений), например недалеко от взлетающего реактивного самолета, соответствуют энергии колебаний порядка 10 -4 Дж.
Кажется, что энергия 10 -4 Дж = 0,1 мДж очень маленькая, но для маленькой и тонкой барабанной перепонки превышение этой энергии может привести к ее разрыву.
Единица громкости называется белом (Б) в честь физика Генриха Бела. На практике чаще используют децибел: 1 дБ = 0,1 Б. На рисунке 230 представлена диаграмма громкости звуков от различных источников. Тиканье часов или шепот на расстоянии I м соответствуют 10 дБ, а звуковая волна громкостью порядка 130 дБ вызывает ощущение боли.
Объективной физической характеристикой звуковой волны, определяющей ее громкость, является интенсивность.
Интенсивностью звука I называется физическая величина, равная энергии, переносимой звуковой волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность определяется по формуле:
где W — энергия звуковой волны, переносимая через поверхность площадью S в течение времени t. Для интенсивности нет специальной единицы измерения, и она измеряется в ваттах на квадратный метр (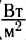
Точечным источником звука называется колебательная система, размеры которой много меньше длины создаваемой ею звуковой волны.
Например, при частоте звука 500 Гц и скорости в воздухе 340 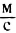
В этом случае волны распространяются как бы из точки и будут сферическими по форме. На расстоянии г от источника площадь сферической поверхности S = 4πr 2 и
где P — мощность источника, т. е. энергия звуковых волн, создаваемая нм в одну секунду.
Если мощность источника постоянна и потерями энергии колебательного движения можно пренебречь, то интенсивность сферической звуковой волны убывает обратно пропорционально квадрату расстояния до источника. При увеличении расстояния в 2 раза интенсивность звука уменьшается в 4 раза.
Как мы уже обсуждали, слуховой аппарат человека и обрабатывающие звуковую информацию системы коры головного мозга способны распознавать лишь звуки в определенных интервалах громкости и частоты.
Под акустическим загрязнением понимают распространение в окружающем человека пространстве очень большого количества шумовых звуков или звуков большой громкости.
При акустическом загрязнении человек не может правильно воспринимать информацию, некоторые люди ощущают боль, может повышаться артериальное давление и т. п.
Например, если в классе звучат два голоса: учитель задает вопросы, а ученик отвечает, то слуховая система всех остальных учеников способна воспринимать, а мозг способен обрабатывать и запоминать информацию, переносимую звуковыми волнами от говорящих. После звонка, на перемене, начинают говорить одновременно практически все находящиеся в классе ученики. В этих условиях услышать, что говорит даже стоящий рядом человек, очень трудно.
В современном городе уровень уличного шума может достигать 80—90 дБ, и это негативно влияет на работу слухового аппарата и мозга человека. Еще больший уровень шума соответствует концерту рок-музыкантов. Поэтому с течением лет чувствительность их слуха снижается, они становятся «тугоухими», т. е. плохо слышат и воспринимают звуки и речь нормальной громкости.
На основании исследований установлены санитарные нормы, согласно которым безопасный уровень громкости звуков для человека не должен превышать 30—40 дБ.
Главные выводы:
- Звуком называется волновой процесс, распространяющийся в твердых телах в виде продольных и поперечных волн, а в жидкостях и газах в виде продольных волн с частотой в пределах от 20 Гц до 20 000 Гц.
- Скорость звуковых волн зависит от упругих свойств и плотности вещества, в которых они распространяются.
- Музыкальные звуки представляют собой гармонические изменяющия звуковые волны.
- При акустическом загрязнении окружающей человека среды может жаться чувствительность его слуховой системы и могут возникать болевые ощущения.
Звуковые явления
Так как скорость звука зависит от упругих свойств среды и ее плотности, то при переходе из одной среды в другую скорость звука скачком изменяется. Поэтому для звуковых волн на границе двух сред могут наблюдаться явления отражения и преломления.
Волна, распространяющаяся из первой среды, вызывает вынужденные колебания частиц второй среды. Колебания этих частиц являются источником новых звуковых волн, которые распространяются не только во второй среде, но и в первой. Так возникают отраженные и преломленные звуковые волны.
Отражение волн можно рассмотреть на следующем примере. Капнем из пипетки маленькую каплю воды в прямоугольную ванночку с водой. От места падения капли начинает распространяться круговая волна, от края ванночки волна отражается и движется в обратном направлении (рис. 231).
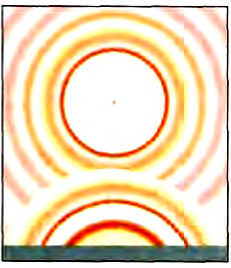
Рис. 232
Эхом называется отраженная звуковая волна, возвратившаяся к источнику звука. В окружающем мире эхо наблюдается при отражении от скал, стен зданий и т. д. (рис. 232). При этом вогнутые арки зданий и каменных мостов отражают звуковые волны лучше всего.

Рис. 232
В закрытом большом помещении, например в театре, может происходить многократное отражение звуковых волн от стен и потолка, поэтому в момент прекращения действия источника звук не сразу исчезает.
Реверберацией (послезвучанием) называется /величение продолжительности звука из-за его отражения от окружающих предметов. Реверберация зависит как от объема помещения, так и от его формы, материала потолка, стен, пола, мебели.
Время реверберации является важнейшей характеристикой тех больших помещений, в которых выступают актеры, ораторы, музыканты, и его следует учитывать при их проектировании. Часто говорят, что в помещении «хорошая акустика», если голос человека без микрофона со сцены можно достаточно хорошо услышать даже на большом удалении от нее.
Если такое помещение заполнено людьми, то время реверберации порядка 2 с, а если помещение пустое, то время реверберации примерно в 2 раза больше.
Эхо может быть использовано для звуколокации, т. е. оценки расстояний до отражающих звуковые волны предметов. Например, можно измерить промежуток времени между моментами испускания звука и моментом его возвращения к источнику после отражения. Пройденный звуком путь s туда и назад одинаков, тогда измеренный промежуток времени:
где 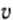
На практике для звуколокации (эхолокации) лучше использовать неслышимые человеком ультразвуки. Это обусловлено тем, что ультразвуковые волны большой мощности можно получать направленными, т. е. в виде узкого пучка волн. Это позволяет не только оценить расстояние, но и определить направление на отражающий звук объект.
Например, для определения глубины водоемов (рис. 233), поиска косяков рыбы и т. п. используются эхолоты — приборы, излучающие ультразвуковые волны и принимающие их после отражения. В живой природе дельфины и летучие мыши используют ультразвуки для ориентации в пространстве и при ловле добычи. 
Рис. 233
Звуколокаторы позволяют находить различные повреждения в изделиях (полости, трещины и т. д).
Ультразвуковая диагностика (УЗИ) (рис. 234) используется в медицине для обнаружения опухолей, заболеваний внутренних органов и т. и.
Если частота звуковой волны совпадает с собственной частотой колебаний какой-либо колебательной системы, то наблюдается акустический резонанс. Например, обычный камертон издает достаточно тихий звук, и поэтому его устанавливают на деревянном ящике (см. рис. 227) с собственной частотой колебаний, равной частоте камертона. Благодаря резонансу стенки ящика колеблются с большой амплитудой, и звук становится гораздо громче, поэтому ящик называют резонатором.
Резонаторами являются корпуса (деки) большинства музыкальных инструментов (рис. 235), а также полости рта и носа человека. В духовых инструментах акустическими резонаторами являются трубы, а явление резонанса наблюдается для колебаний воздуха, который их заполняет.

Рис. 235
В последнее время большое значение приобрело изучение и использование инфразвуков: v
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
Урок 325. Колебательное движение и его характеристикиСкачать




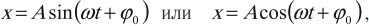
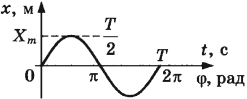
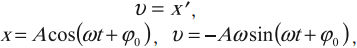
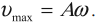
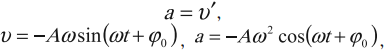
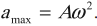
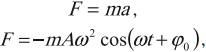
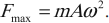
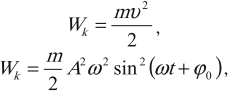
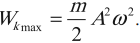
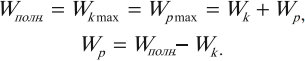
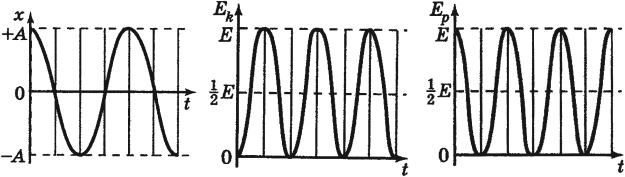
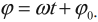




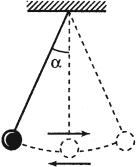
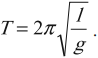
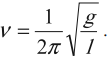
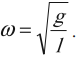
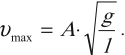
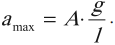
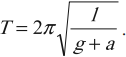
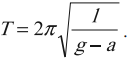
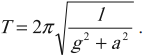
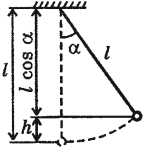
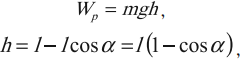
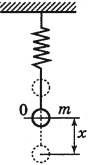
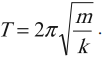
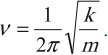
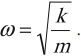
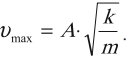
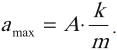
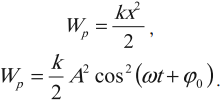
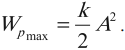
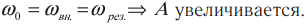
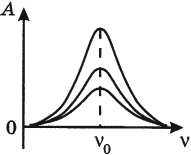
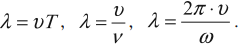
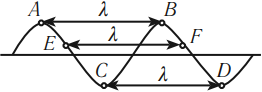
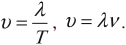


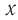 , проекция скорости
, проекция скорости 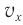 , проекция действующей силы
, проекция действующей силы 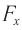 ) принимают одинаковые значения через равные промежутки времени
) принимают одинаковые значения через равные промежутки времени 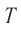 (рис. 1), называется периодическим.
(рис. 1), называется периодическим.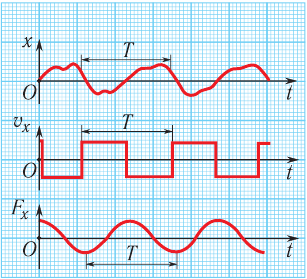
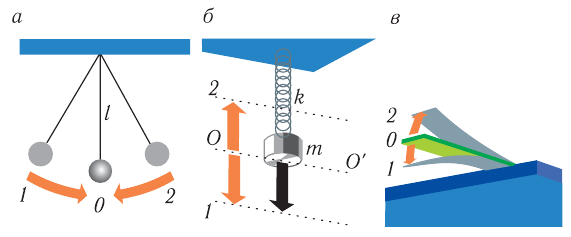
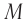 по окружности радиусом
по окружности радиусом 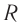 (рис. 3, а). Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем ось
(рис. 3, а). Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем ось 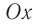 , как показано на рисунке 3, а. Если в начальный момент времени
, как показано на рисунке 3, а. Если в начальный момент времени 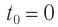 материальная точка находилась в положении
материальная точка находилась в положении 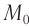 , то через промежуток времени
, то через промежуток времени 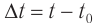 она окажется в некотором положении
она окажется в некотором положении 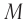 .
.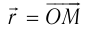 движущейся точки, ее линейную скорость
движущейся точки, ее линейную скорость 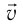 и центростремительное ускорение
и центростремительное ускорение 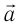 . Проекция
. Проекция 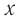 радиус-вектора в положении
радиус-вектора в положении 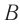 ) является смещением материальной точки от центра окружности
) является смещением материальной точки от центра окружности 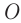 вдоль оси
вдоль оси 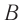 .
.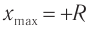 до
до 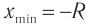 , то можно сказать, что точка
, то можно сказать, что точка 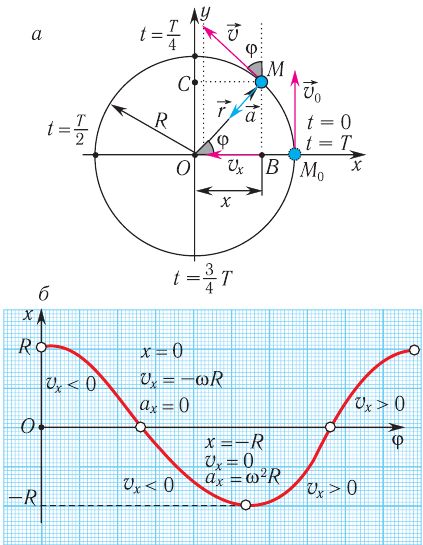
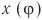 , соответствующая движению по окружности.
, соответствующая движению по окружности.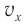 точки В и периодически изменяется
точки В и периодически изменяется 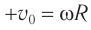 до
до 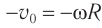 , а проекция ее центростремительного ускорения — проекцией ускорения
, а проекция ее центростремительного ускорения — проекцией ускорения 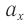 точки
точки 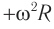 до
до 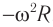 .
.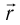 за промежуток времени
за промежуток времени 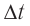 повернулся на угол
повернулся на угол 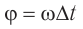 (см. рис. 3, а). При равномерном вращении точки
(см. рис. 3, а). При равномерном вращении точки 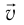 направлена по касательной, а центростремительное ускорение
направлена по касательной, а центростремительное ускорение 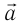 — к центру окружности (см. рис. 3, а). Таким образом,
— к центру окружности (см. рис. 3, а). Таким образом,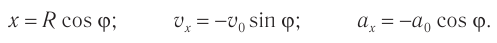
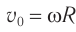 , модуль центростремительного ускорения
, модуль центростремительного ускорения 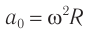 и
и 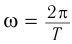 , выполняются соотношения:
, выполняются соотношения: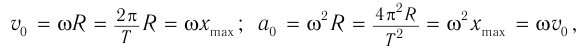
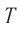 — период вращения тела по окружности.
— период вращения тела по окружности.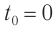 материальная точка находилась в точке
материальная точка находилась в точке 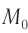 , то координату
, то координату 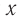 , проекции скорости
, проекции скорости 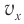 и ускорения
и ускорения 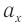 точки
точки 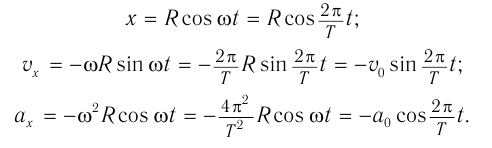
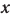 , проекции скорости
, проекции скорости 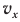 и ускорения
и ускорения 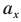 тела, движущегося движущегося по окружности, в разные моменты времени
тела, движущегося движущегося по окружности, в разные моменты времени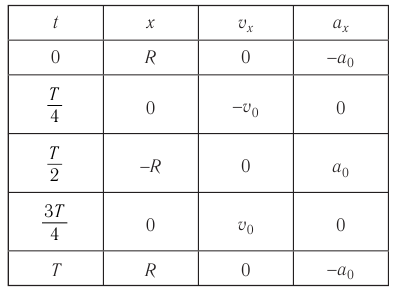
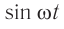 и
и 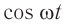 периодические, то через промежуток времени, равный периоду
периодические, то через промежуток времени, равный периоду 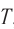 , по истечении которого угол
, по истечении которого угол 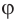 изменится на
изменится на 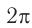 , все характеристики движения точки
, все характеристики движения точки 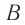 вдоль оси
вдоль оси 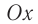 (координата, проекция скорости и проекция ускорения) примут прежние значения (табл. 1), т. е. значения характеристик периодически повторяются.
(координата, проекция скорости и проекция ускорения) примут прежние значения (табл. 1), т. е. значения характеристик периодически повторяются.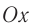 (см. рис. 3, а). Как отмечалось выше, повторяемость — основной признак периодического движения.
(см. рис. 3, а). Как отмечалось выше, повторяемость — основной признак периодического движения.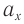 от времени показаны на рисунке 4, где
от времени показаны на рисунке 4, где 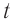 — время, отсчитываемое от момента начала колебаний.
— время, отсчитываемое от момента начала колебаний.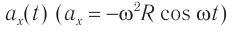 точки
точки 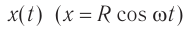 и противоположна ему по знаку:
и противоположна ему по знаку: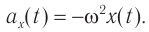
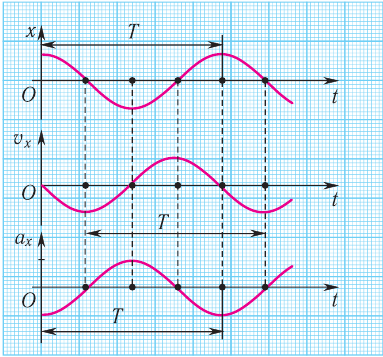
 от времени при колебательном движении материальной точки
от времени при колебательном движении материальной точки
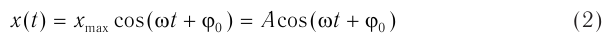
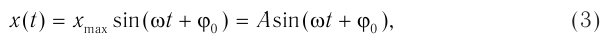
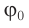 — начальная фаза, которая определяет состояние колебательной системы в начальный момент времени,
— начальная фаза, которая определяет состояние колебательной системы в начальный момент времени, 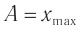 — амплитуда колебаний.
— амплитуда колебаний.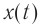 (соотношения (2) и (3)) называется кинематическим законом (или уравнением) гармонических колебаний (законом движения), поскольку позволяет определить положение тела, его скорость, ускорение в произвольный момент времени.
(соотношения (2) и (3)) называется кинематическим законом (или уравнением) гармонических колебаний (законом движения), поскольку позволяет определить положение тела, его скорость, ускорение в произвольный момент времени.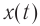 — координата
— координата  (смещение из положения равновесия) в момент времени
(смещение из положения равновесия) в момент времени 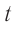 :
: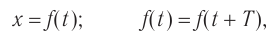
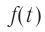 — заданная периодическая функция времени
— заданная периодическая функция времени 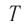 — период этой функции.
— период этой функции.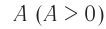 — амплитуда колебаний — максимальное смещение
— амплитуда колебаний — максимальное смещение 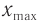 тела или системы тел из положения устойчивого равновесия.
тела или системы тел из положения устойчивого равновесия.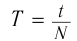 — период — длительность одного полного колебания, т. е. наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание. Здесь
— период — длительность одного полного колебания, т. е. наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание. Здесь 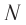 полных колебаний.
полных колебаний.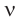 — частота — число полных колебаний, совершаемых в единицу времени:
— частота — число полных колебаний, совершаемых в единицу времени: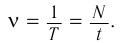
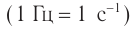 .
.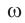 — циклическая частота — число полных колебаний, совершаемых за промежуток времени
— циклическая частота — число полных колебаний, совершаемых за промежуток времени 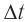 , равный
, равный 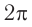 секунд:
секунд: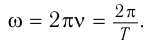
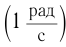 .
.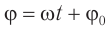 — фаза (от греч.
— фаза (от греч. 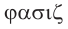 (фазис) — появление, момент явления) — аргумент периодической функции, определяющий значение физической величины в любой момент времени
(фазис) — появление, момент явления) — аргумент периодической функции, определяющий значение физической величины в любой момент времени 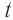 . Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной частоте и амплитуде.
. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной частоте и амплитуде.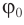 — начальная фаза, которая определяет состояние колебательной системы в начальный момент времени
— начальная фаза, которая определяет состояние колебательной системы в начальный момент времени 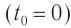 .
.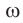 гармонических колебаний зависит только от свойств системы, в которой происходят колебания, но не зависит от амплитуды колебаний. Амплитуда колебаний
гармонических колебаний зависит только от свойств системы, в которой происходят колебания, но не зависит от амплитуды колебаний. Амплитуда колебаний 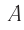 и начальная фаза
и начальная фаза 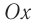 можно записать:
можно записать: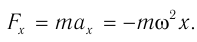
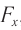 , возвращающей тело в положение равновесия
, возвращающей тело в положение равновесия 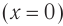 , пропорциональна его смещению от этого положения (координате)
, пропорциональна его смещению от этого положения (координате)  , причем знак «минус» отражает «возвратный» характер возникающей силы. Как уже отмечалось, появление возвращающей силы при отклонении тела от положения равновесия является необходимым условием возникновения колебаний.
, причем знак «минус» отражает «возвратный» характер возникающей силы. Как уже отмечалось, появление возвращающей силы при отклонении тела от положения равновесия является необходимым условием возникновения колебаний.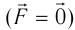 . Координату этой точки, как правило, принимают равной нулю
. Координату этой точки, как правило, принимают равной нулю 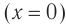 .
.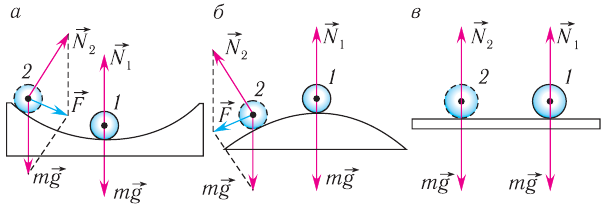
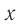 вращающейся по окружности материальной точки
вращающейся по окружности материальной точки 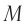 , можно рассматривать и изменение ее координаты
, можно рассматривать и изменение ее координаты 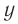 (точка
(точка 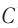 ) (см. рис. 3, а). Следовательно, точка
) (см. рис. 3, а). Следовательно, точка  будет совершать гармонические колебания вдоль оси
будет совершать гармонические колебания вдоль оси  .
.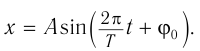
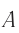 — амплитуда колебаний тела,
— амплитуда колебаний тела, 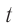 — время, отсчитываемое с момента прохождения телом положения равновесия,
— время, отсчитываемое с момента прохождения телом положения равновесия, 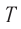 — период колебаний,
— период колебаний, 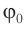 — начальная фаза.
— начальная фаза.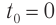 , тогда
, тогда 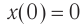 и
и 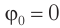 .
.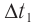 , необходимый телу для прохождения расстояния из среднего положения в крайнее
, необходимый телу для прохождения расстояния из среднего положения в крайнее 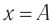 , определяется из уравнения:
, определяется из уравнения: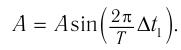
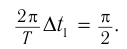
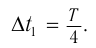
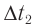 , необходимый для прохождения первой половины этого расстояния
, необходимый для прохождения первой половины этого расстояния 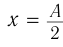 определяется из уравнения:
определяется из уравнения: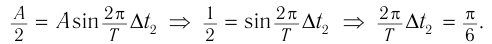
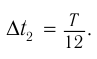
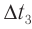 , необходимый для прохождения второй половины этого расстояния, определяется из соотношения:
, необходимый для прохождения второй половины этого расстояния, определяется из соотношения: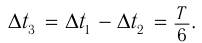
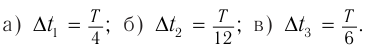
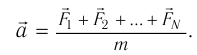
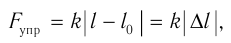
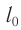 — длина недеформированного тела,
— длина недеформированного тела, 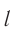 — длина деформированного тела.
— длина деформированного тела.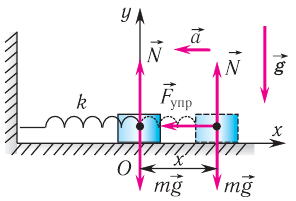
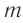 , лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью
, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью 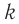 (рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).
(рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).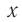 вправо (см. рис. 6). Тогда в пружине возникнет сила упругости
вправо (см. рис. 6). Тогда в пружине возникнет сила упругости 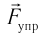 , действующая на груз и направленная влево.
, действующая на груз и направленная влево.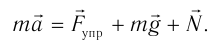
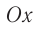 действующих на груз сил (см. рис. 6) с учетом закона Гука получаем:
действующих на груз сил (см. рис. 6) с учетом закона Гука получаем: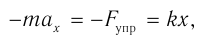
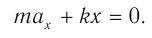

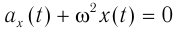 , находим циклическую частоту колебаний горизонтального пружинного маятника:
, находим циклическую частоту колебаний горизонтального пружинного маятника:
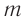 груза и жесткостью
груза и жесткостью 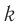 пружины.
пружины.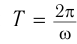 , подставив в нее выражение (2):
, подставив в нее выражение (2):
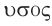 (изос) — равный и
(изос) — равный и  (хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.
(хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.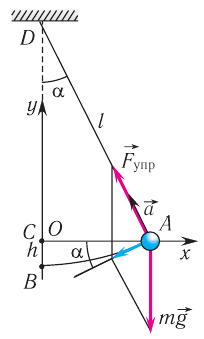
 (см. рис. 7), который нить образует с вертикалью.
(см. рис. 7), который нить образует с вертикалью. и направленная вдоль нити сила упругости
и направленная вдоль нити сила упругости 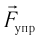 . Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
. Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
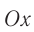 и
и 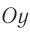 (см. рис. 7) получаем:
(см. рис. 7) получаем: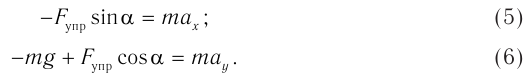
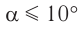 значения
значения 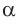 и
и 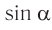 различаются меньше чем на
различаются меньше чем на 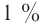 . Поэтому при малых углах отклонения
. Поэтому при малых углах отклонения 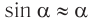 и длина дуги
и длина дуги 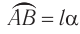 очень мало отличается от длины хорды
очень мало отличается от длины хорды 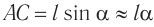 , где угол
, где угол 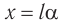 . Но практически маятник движется вдоль оси
. Но практически маятник движется вдоль оси 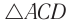 находим
находим 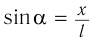 и, подставив это выражение в (5), получим:
и, подставив это выражение в (5), получим: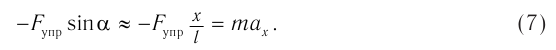
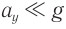 и ею можно пренебречь, а
и ею можно пренебречь, а 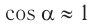 , тогда из уравнения (6) следует, что
, тогда из уравнения (6) следует, что 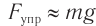 .
.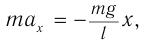
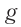 — ускорение, сообщаемое грузу маятника силой упругости нити.
— ускорение, сообщаемое грузу маятника силой упругости нити.
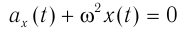 можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой
можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой

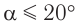 погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает
погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает 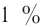 .
.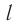 и модулем ускорения свободного падения
и модулем ускорения свободного падения 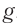 .
.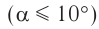 математического маятника длиной
математического маятника длиной 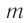 и амплитуды колебаний (угла начального отклонения
и амплитуды колебаний (угла начального отклонения 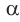 ). Он установил также, что период этих колебаний прямо пропорционален
). Он установил также, что период этих колебаний прямо пропорционален 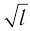 .
.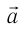 , обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
, обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле: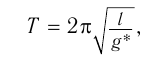
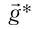 — «эффективное ускорение», равное векторной разности
— «эффективное ускорение», равное векторной разности 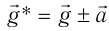 .
.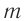 и жесткость пружины
и жесткость пружины 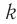 .
.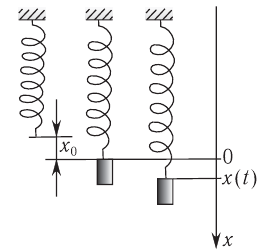
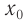 , определяемую соотношением:
, определяемую соотношением:
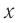 из положения равновесия сила, действующая со стороны пружины на груз, равна
из положения равновесия сила, действующая со стороны пружины на груз, равна 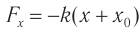 .
.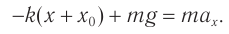
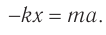
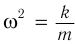 , то уравнение движения груза запишется в виде:
, то уравнение движения груза запишется в виде: 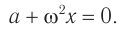
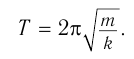
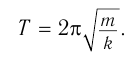
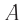 , циклическую частоту
, циклическую частоту 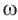 , период
, период 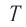 и начальную фазу
и начальную фазу 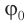 колебаний тела массой
колебаний тела массой 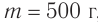 , подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние
, подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние 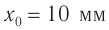 и для возбуждения колебаний его смещают вниз на расстояние
и для возбуждения колебаний его смещают вниз на расстояние 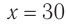 от положения равновесия и отпускают.
от положения равновесия и отпускают.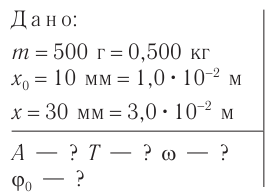
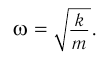
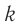 пружины запишем условие равновесия тела:
пружины запишем условие равновесия тела: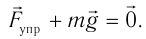
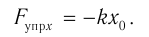
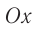 условие равновесия запишется:
условие равновесия запишется: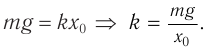
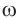 получаем:
получаем: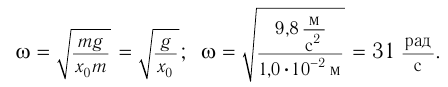
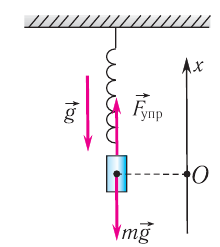
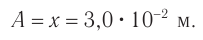
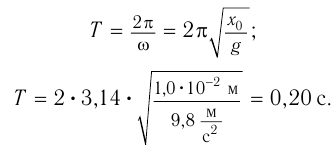
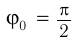 .
.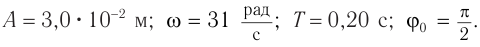
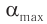 (рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
(рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю: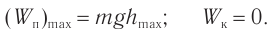
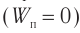 , то из закона сохранения механической энергии следует (см. рис. 10), что
, то из закона сохранения механической энергии следует (см. рис. 10), что 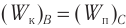 , т. е. кинетическая энергия маятника (а следовательно, и скорость) будет максимальна:
, т. е. кинетическая энергия маятника (а следовательно, и скорость) будет максимальна: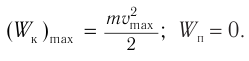
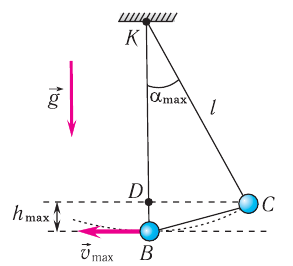
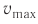 и
и 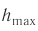 .
.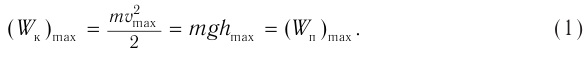

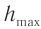 можно выразить через длину
можно выразить через длину 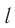 маятника и амплитуду
маятника и амплитуду 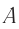 колебаний. Если колебания малые, то
колебаний. Если колебания малые, то 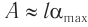 . Из
. Из 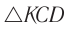 (см. рис. 10) находим:
(см. рис. 10) находим: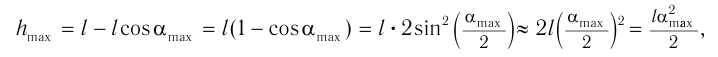
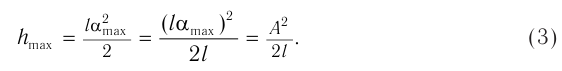

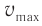 в соотношение (1), находим:
в соотношение (1), находим: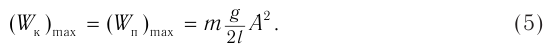
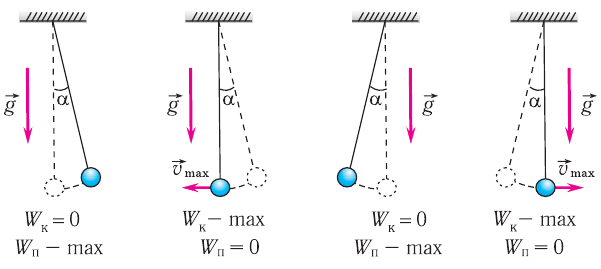
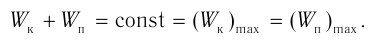
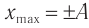 , модуль скорости маятника
, модуль скорости маятника 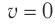 , и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:
, и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:
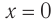 , вся энергия пружинного маятника переходит в кинетическую энергию груза:
, вся энергия пружинного маятника переходит в кинетическую энергию груза: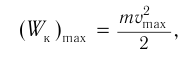
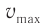 — модуль максимальной скорости груза при колебаниях.
— модуль максимальной скорости груза при колебаниях.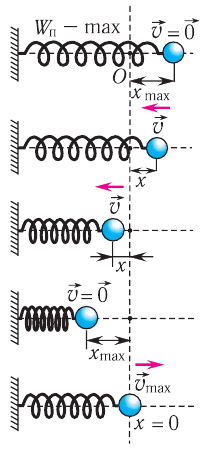
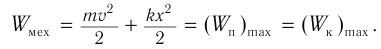
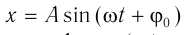 и проекции скорости груза
и проекции скорости груза 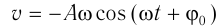 , а также для
, а также для 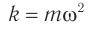 находим его потенциальную энергию
находим его потенциальную энергию 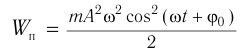 и кинетическую энергию
и кинетическую энергию 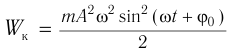 в произвольный момент времени
в произвольный момент времени 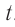 .
.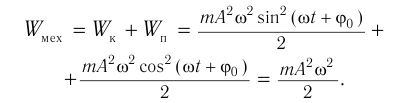
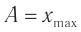 определяет начальную потенциальную, а начальная скорость
определяет начальную потенциальную, а начальная скорость 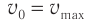 определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.
определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.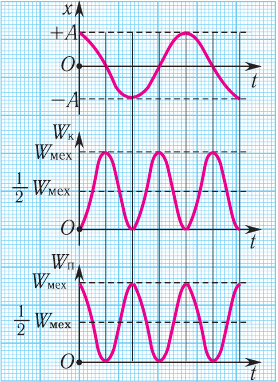
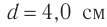 и при прохождении положения равновесия достигает скорости, модуль которой
и при прохождении положения равновесия достигает скорости, модуль которой 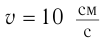 . Определите период
. Определите период 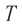 колебаний маятника.
колебаний маятника.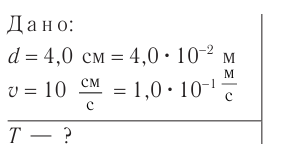
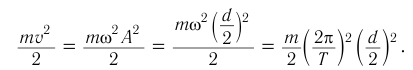
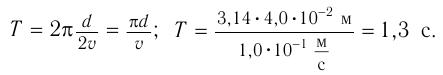
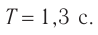
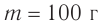 находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью
находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью 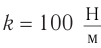 . Его смещают на расстояние
. Его смещают на расстояние 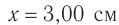 от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой
от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой 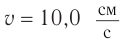 . Определите потенциальную
. Определите потенциальную 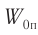 и кинетическую
и кинетическую 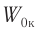 энергию груза в начальный момент времени. Запишите кинематический закон движения груза.
энергию груза в начальный момент времени. Запишите кинематический закон движения груза.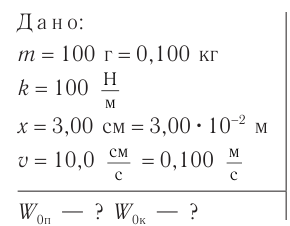
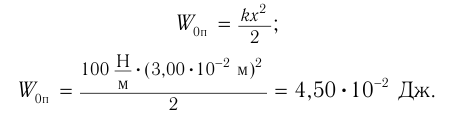
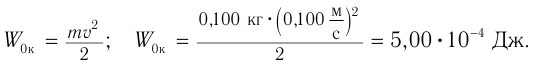
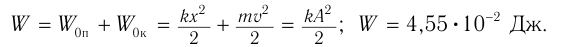
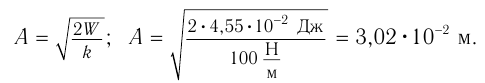
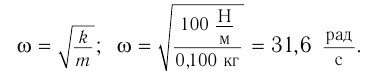
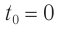 координата груза
координата груза 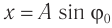 . Отсюда начальная фаза:
. Отсюда начальная фаза: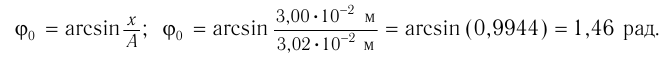
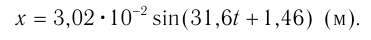
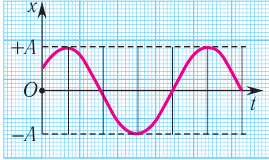
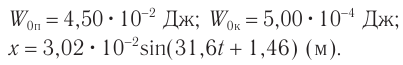
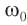 , называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.
, называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.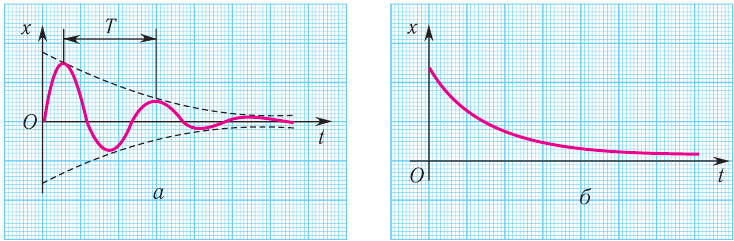
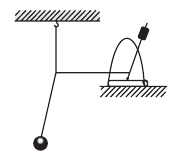
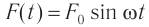 или
или 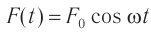 . Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
. Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.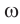 вынуждающей силы и частота
вынуждающей силы и частота 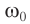 собственных колебаний, а также от величины трения в системе.
собственных колебаний, а также от величины трения в системе.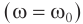 (рис. 17).
(рис. 17).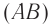 четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.
четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.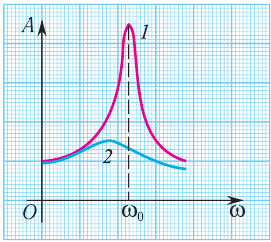
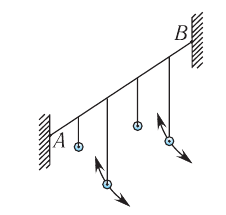
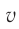 движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника
движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника 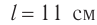 , длина рельса
, длина рельса 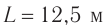 .
.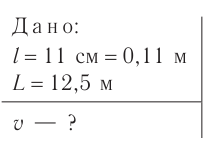
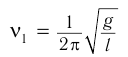
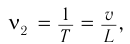
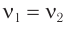 .
.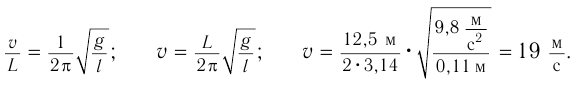
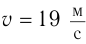 .
.
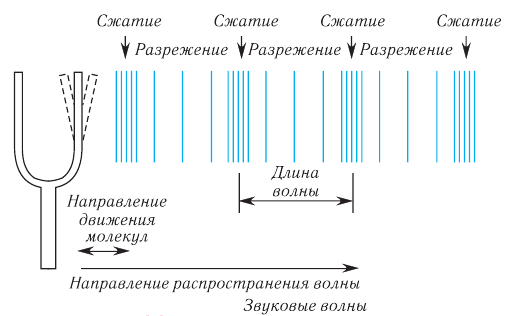
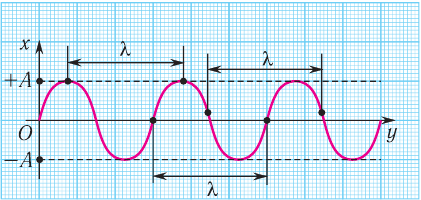
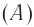 — модуль максимального смещения точек среды из положений равновесия при колебаниях;
— модуль максимального смещения точек среды из положений равновесия при колебаниях;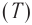 — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны):
— время полного колебания (период колебаний точек среды равен периоду колебаний источника волны):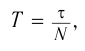
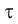 — промежуток времени, в течение которого совершаются
— промежуток времени, в течение которого совершаются 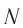 колебаний;
колебаний;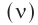 — число полных колебаний, совершаемых в данной точке в единицу времени:
— число полных колебаний, совершаемых в данной точке в единицу времени: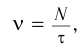
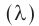 — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника:
— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника: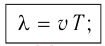
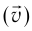 — это скорость распространения гребня волны или любой другой точки волны с определенной фазой (это не скорость частиц), модуль этой скорости:
— это скорость распространения гребня волны или любой другой точки волны с определенной фазой (это не скорость частиц), модуль этой скорости: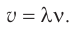
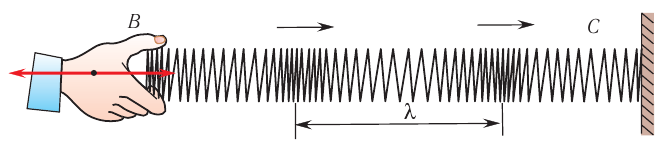
 пружины мы вызовем появление волны (рис. 22). При этом каждый виток пружины будет колебаться вдоль направления распространения волны
пружины мы вызовем появление волны (рис. 22). При этом каждый виток пружины будет колебаться вдоль направления распространения волны  . Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды и не могут возникать при сдвиге частиц жидкости или газа. Поэтому в таких средах возможно распространение только продольных волн.
. Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды и не могут возникать при сдвиге частиц жидкости или газа. Поэтому в таких средах возможно распространение только продольных волн.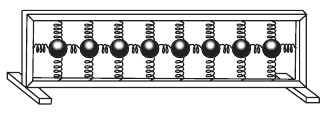
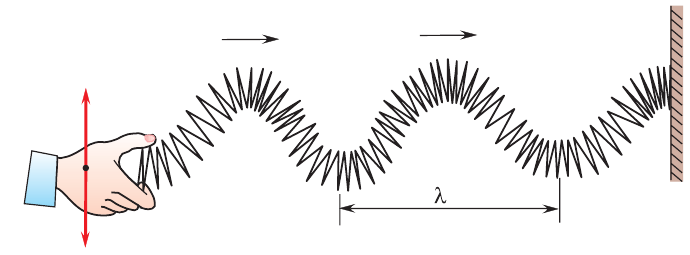
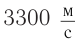 , а продольные
, а продольные 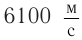 .
.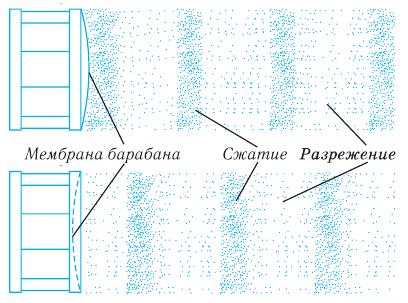
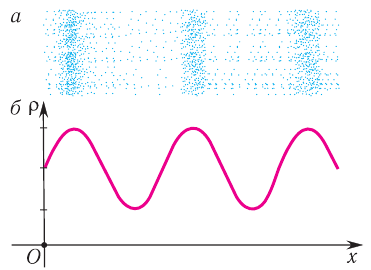
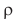 воздуха от координаты
воздуха от координаты 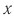 в продольной волне
в продольной волне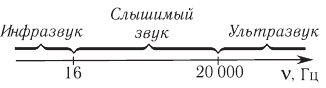
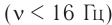 ;
;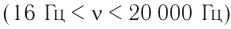 ;
;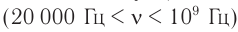 ;
;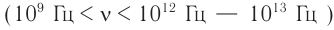 .
. , а летучие мыши — до
, а летучие мыши — до  . Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.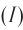 , определяемое как энергия
, определяемое как энергия 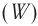 , переносимая волной в единицу времени
, переносимая волной в единицу времени 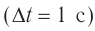 через поверхность площадью
через поверхность площадью 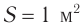 , расположенную перпендикулярно к направлению распространения волны:
, расположенную перпендикулярно к направлению распространения волны: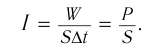
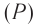 , переносимую волнами через поверхность единичной площади перпендикулярно к направлению распространения волны.
, переносимую волнами через поверхность единичной площади перпендикулярно к направлению распространения волны.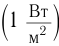 .
.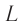 определяют обычно, используя шкалу, единицей которой является 1 бел
определяют обычно, используя шкалу, единицей которой является 1 бел 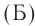 или ее дольная единица — 1 децибел
или ее дольная единица — 1 децибел 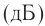 (одна десятая бела). Уровень интенсивности самого слабого звука, который воспринимает наше ухо, соответствует 1 белу
(одна десятая бела). Уровень интенсивности самого слабого звука, который воспринимает наше ухо, соответствует 1 белу 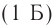 . Единица названа в честь изобретателя телефона Александра Белла.
. Единица названа в честь изобретателя телефона Александра Белла.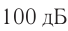 , мощные усилители —
, мощные усилители — 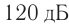 , а реактивный самолет —
, а реактивный самолет — 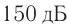 . Тем, кто при работе подвергается воздействию шума свыше
. Тем, кто при работе подвергается воздействию шума свыше 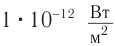 (порог слышимости) до
(порог слышимости) до 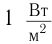 (порог болевого ощущения) (рис. 28).
(порог болевого ощущения) (рис. 28).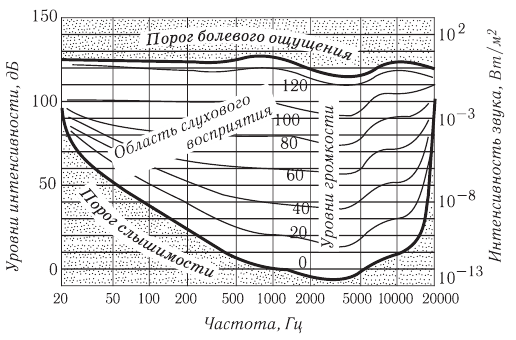
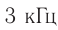 , так как интенсивности порядка
, так как интенсивности порядка 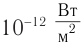 уже достаточно, чтобы ухо восприняло звук. А для того, чтобы услышать звук на частоте
уже достаточно, чтобы ухо восприняло звук. А для того, чтобы услышать звук на частоте 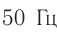 , его интенсивность должна быть примерно в
, его интенсивность должна быть примерно в 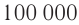 раз больше, т. е. порядка
раз больше, т. е. порядка 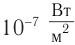 .
.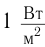 .
.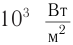 , мощные усилители на концерте в закрытом помещении — до
, мощные усилители на концерте в закрытом помещении — до 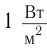 , поезд метро —
, поезд метро — 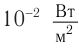 .
.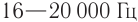 ;
; до
до  .
. . Вследствие этого звук в
. Вследствие этого звук в  оказывается в 100 раз интенсивнее звука в
оказывается в 100 раз интенсивнее звука в  .
.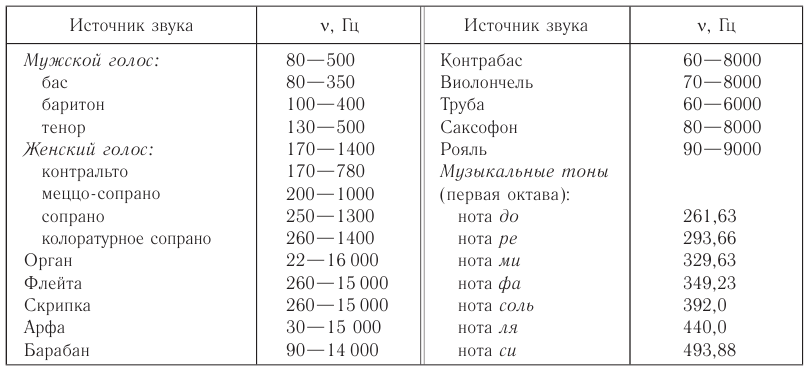
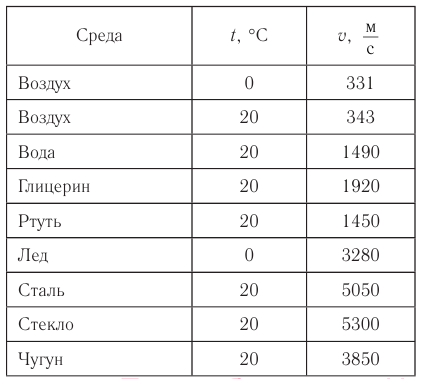
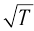 , где
, где 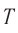 — абсолютная температура. В воздухе модуль скорости звука
— абсолютная температура. В воздухе модуль скорости звука 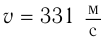 при температуре
при температуре 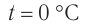 и
и 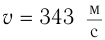 при температуре
при температуре 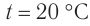 . В жидкостях и металлах модуль скорости звука, как правило, уменьшается с ростом температуры (исключение — вода).
. В жидкостях и металлах модуль скорости звука, как правило, уменьшается с ростом температуры (исключение — вода).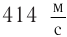 .
.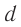 детали и глубину
детали и глубину 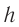 расположения дефекта, если после излучения ультразвукового сигнала получены два отраженных сигнала через промежутки времени
расположения дефекта, если после излучения ультразвукового сигнала получены два отраженных сигнала через промежутки времени 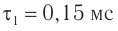 и
и 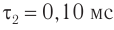 . Модуль скорости распространения ультразвука
. Модуль скорости распространения ультразвука 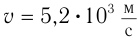 .
.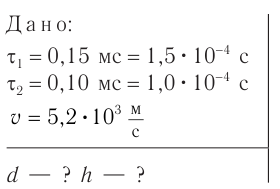
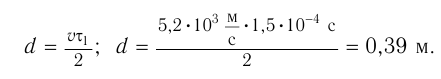
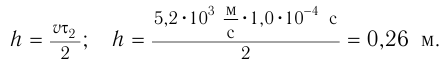
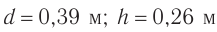 .
.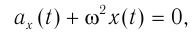
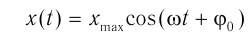
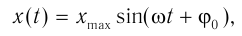
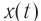 называется кинематическим законом гармонических колебаний (законом движения).
называется кинематическим законом гармонических колебаний (законом движения).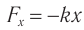 , направленной к положению равновесия колеблющегося тела.
, направленной к положению равновесия колеблющегося тела.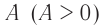 — максимальное смещение
— максимальное смещение 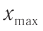 тела или системы тел из положения равновесия.
тела или системы тел из положения равновесия.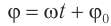 определяет состояние колебательной системы (координаты, скорость, ускорение) в любой момент времени при заданной амплитуде. В начальный момент времени
определяет состояние колебательной системы (координаты, скорость, ускорение) в любой момент времени при заданной амплитуде. В начальный момент времени 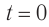 она равна начальной фазе
она равна начальной фазе 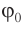 .
.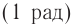 .
.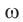 — число полных колебаний за промежуток времени
— число полных колебаний за промежуток времени 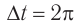 секунд:
секунд: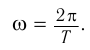
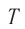 — время одного полного колебания:
— время одного полного колебания: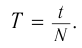
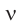 — число полных колебаний, совершаемых в единицу времени:
— число полных колебаний, совершаемых в единицу времени: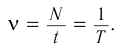
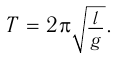
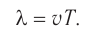
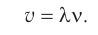



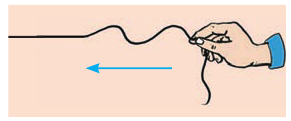
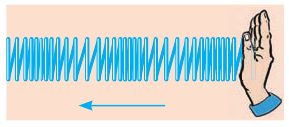
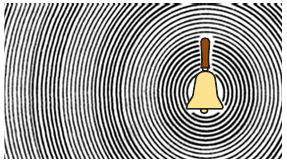
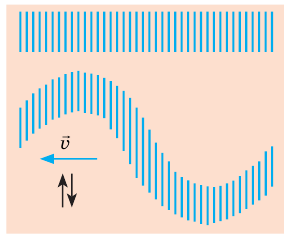
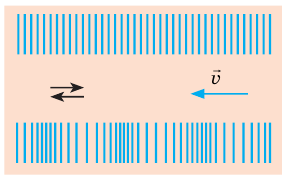
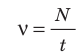
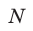 — количество колебаний за интервал времени
— количество колебаний за интервал времени 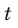
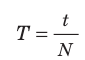
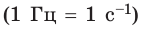
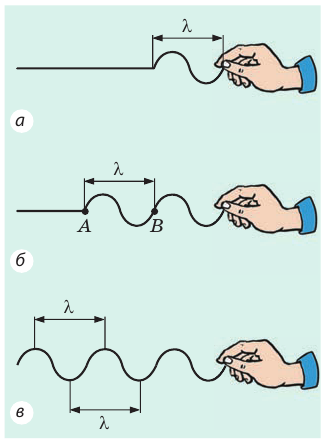
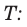
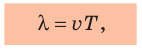
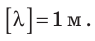
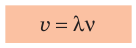
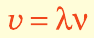
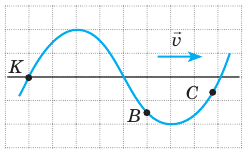
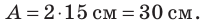
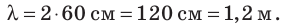
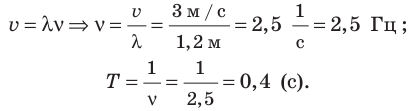
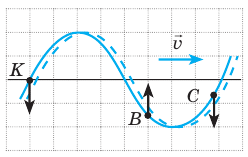
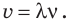
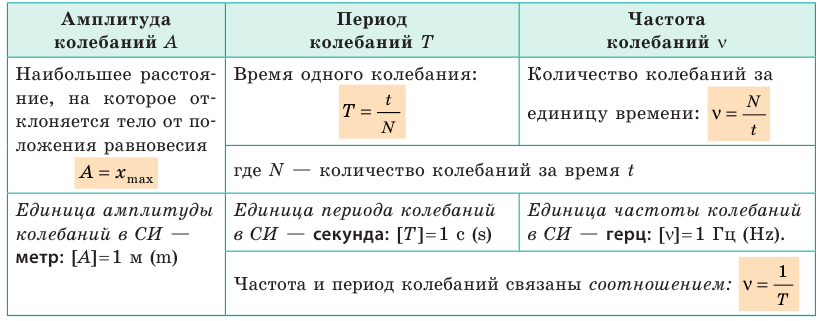
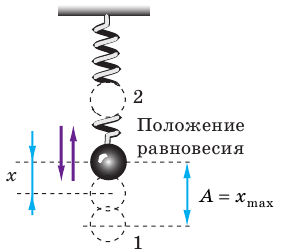
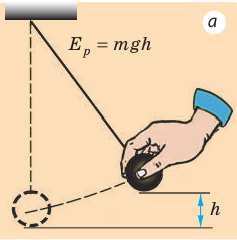
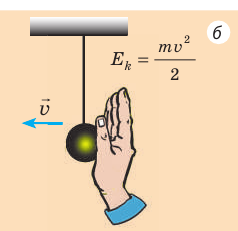
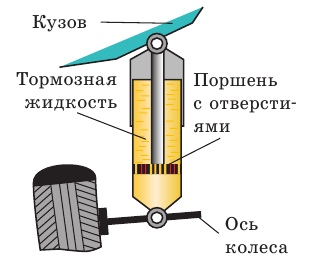
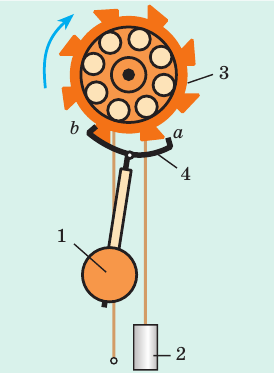
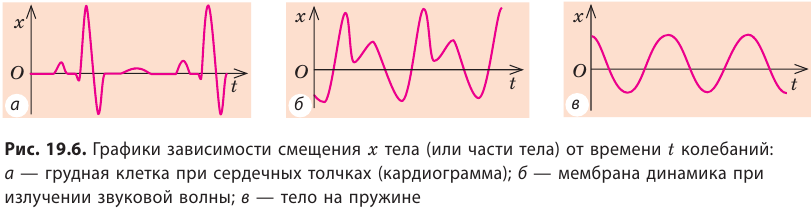
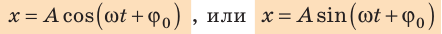

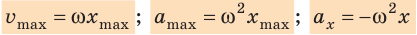
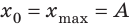 ), то уравнение колебаний удобнее записывать в виде:
), то уравнение колебаний удобнее записывать в виде: 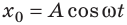 (рис. 19.7, а).
(рис. 19.7, а).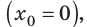 то уравнение колебаний удобнее записывать в виде: x = Asinωt (рис. 19.7, б).
то уравнение колебаний удобнее записывать в виде: x = Asinωt (рис. 19.7, б).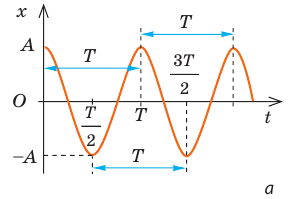
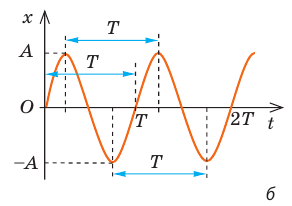
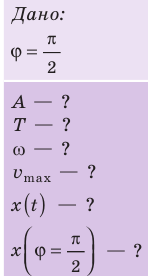
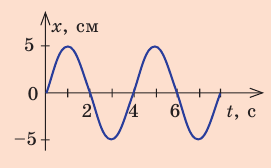
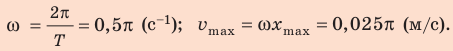
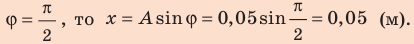
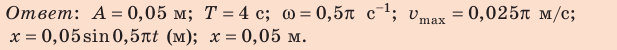
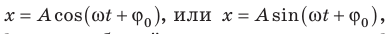 , где A — амплитуда колебаний;
, где A — амплитуда колебаний; 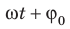 — фаза колебаний
— фаза колебаний 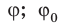 — начальная фаза; ω — циклическая частота.
— начальная фаза; ω — циклическая частота.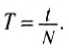
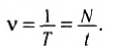
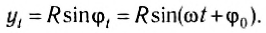
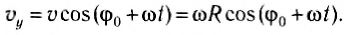
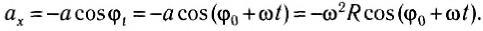
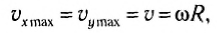
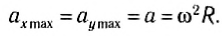
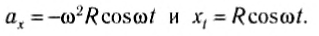
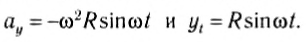
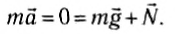
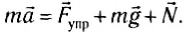
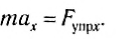
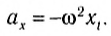
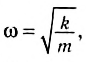
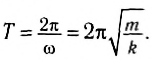
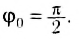
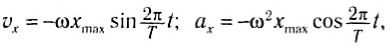
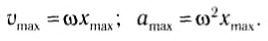
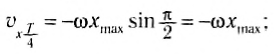
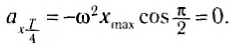
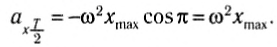
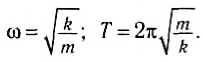
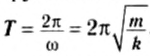 , амплитуда колебаний определяется причинами, которые вывели маятник из положения равновесия.
, амплитуда колебаний определяется причинами, которые вывели маятник из положения равновесия.