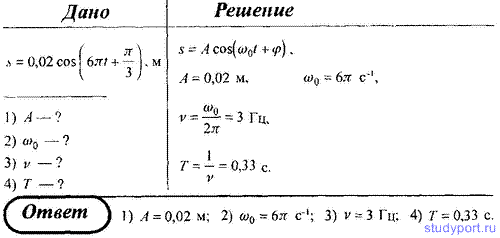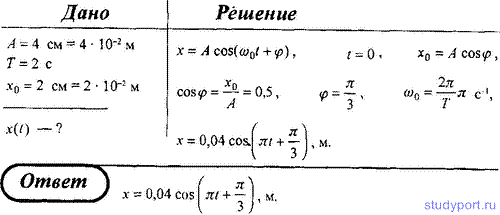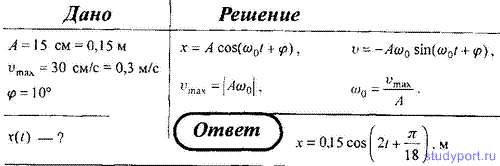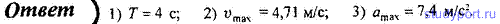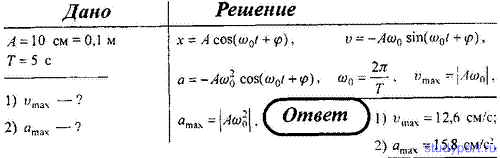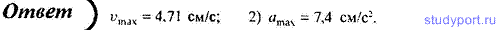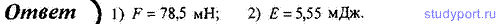Колебание материальной точки задано уравнением x 20 cos 4t 30sin4t (7 видео)

Колебание материальной точки задано уравнением x 20 cos 4t 30sin4t

Глава 13. Динамика точки.

13.4. Свободные незатухающие колебания.

13.4.15. Определить угловую частоту свободных вертикальных колебаний тела, подвешенного к пружине, если в статическом положении тела деформация пружины равна 14 см. (Ответ 8,37)

13.4.16. Определить угловую частоту свободных вертикальных колебаний груза массой m = 5 кг, подвешенного на трех пружинах, если их коэффициенты жесткости с₁ = с₂ = с₃ = 490 Н/м.
(Ответ 5,72)

13.4.17. Определить угловую частоту свободных вертикальных колебаний груза массой m = 2 кг, если коэффициенты жесткости пружин с₁ = с₂ =с₃ = 300 Н/м. (Ответ 10)

13.4.18. Дифференциальное уравнение у + 9у = 0 описывает свободные вертикальные колебания материальной точки. Определить угловую частоту колебаний. (Ответ 3)

13.4.19. Тело, подвешенное к пружине с коэффициентом жесткости с = 700 Н/м, совершает свободные вертикальные колебания С амплитудой 0,2 м. Определить массу тела, если колебания начались из положения статического равновесия с начальной скоростью 4 м/с. (Ответ 1,75)

13.4.20. Тело массой m = 0,3 кг подвешено к пружине и совершает свободные вертикальные колебания с амплитудой 0,4 м. Определить коэффициент жесткости пружины, если колебания начались из положения статического равновесия с начальной скоростью 3 м/с. (Ответ 16,9)

13.4.21. Определить частоту свободных вертикальных колебании груза массой m = 10 кг, подвешенного на двух пружинах, если их приведенный коэффициент жесткости равен 3,6 Н/см. (Ответ 0,955)

13.4.22. Колебание материальной точки задано уравнением х = 20 cos 4t + 30 sin 4t, где x — в см. Определить амплитуду колебаний в см. (Ответ 36,1)

13.4.23. Определить модуль начальной скорости материальной точки, при которой ее свободные колебания будут соответствовать закону движения, заданному графиком функции у = y(t) (Ответ -1,05)

13.4.24. Груз массой m = 9 кг подвешен к пружине с коэффициентом жесткости с = 90 Н/м и совершает свободные вертикальные колебания с амплитудой 0,1 м. Определить начальную скорость груза, если колебания начались из положения статического равновесия. (Ответ 0,316)

13.4.25. Груз массой m = 3 кг подвешен к пружине с коэффициентом жест кости с = 300 Н/м и находится в свободном прямолинейном вертикальном колебательном движении. Определить амплитуду колебаний груза в см. если в момент времени t₀ = 0 его скорость v₀ = 2 м/с, а смещение от положения статического равновесия x₀ = 0,3 м. (Ответ 36,1)

Содержание

Производная 20*cos(4*t)+30*sin(4*t)
Решение
Механические и электромагнитные колебания
📺 Видео

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Производная 20cos(4t)+30sin(4t)

Решение

Производная произведения константы на функцию есть произведение этой константы на производную данной функции.

Производная косинус есть минус синус:

Затем примените цепочку правил. Умножим на :

В силу правила, применим: получим

Таким образом, в результате:

В результате последовательности правил:

Таким образом, в результате:

Производная синуса есть косинус:

Затем примените цепочку правил. Умножим на :

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Механические и электромагнитные колебания

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

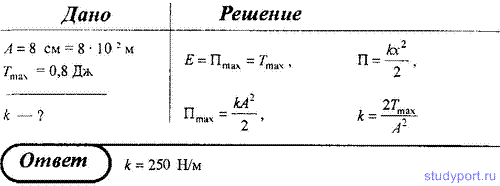
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

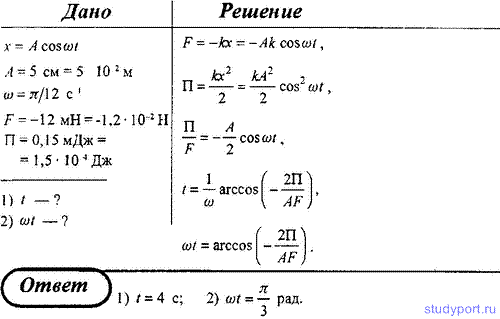
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с -1 . Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.