2. Возведение обеих частей уравнения в квадрат.
Пусть даны два уравнения 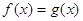
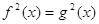
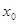
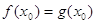
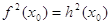
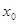
В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.
Пример 1. Решить уравнение 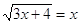
Решение. Возведем обе части этого уравнения в квадрат.
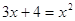
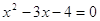
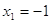
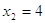
Если 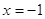
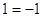
Если 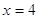
Следовательно, уравнение имеет единственный корень: 4.
3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.
Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения — следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.
Пример 1. Решить уравнение 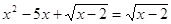
Решение. Выполнив приведение подобных слагаемых, получим: 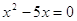
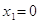
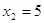
Если 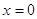
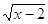
Если 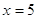
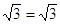
Следовательно, уравнение имеет единственный корень:5.
Пример 2. Решить уравнение 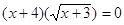
Решение. 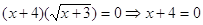
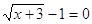
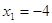
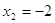
Если 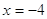
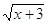
Если 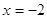
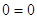
Следовательно, уравнение имеет единственный корень:-2.
Если при решении уравнения мы заменили его уравнением — следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.
Рассмотрим уравнение 
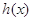
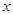
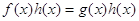
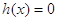
Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение 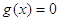
Теорема 1. Если обе части уравнения умножить на 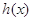
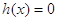
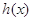
Пример 1. 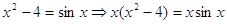
Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение 
Пример 2. Уравнение 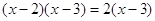
Деление обеих частей уравнения на 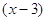
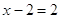
Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение: 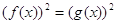
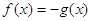
Пример 3. Уравнение 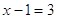
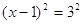
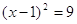
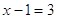
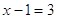
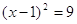
Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.
Пример 1. 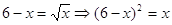
При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.
Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: 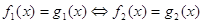
Пример 1. Уравнения 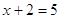
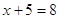
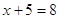
Пример 2. Уравнения 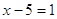
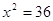
Пример 3. Уравнения 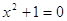
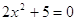
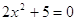
Определение 11. Пусть даны уравнения 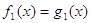
Пример 1. 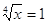
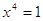
Отметим, что часто множество М совпадает либо с ОДЗ уравнения 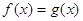
Имеется ряд теорем о равносильности уравнений.
Теорема 3. При возведении обеих частей уравнения в одну и ту же нечетную степень получается уравнение, равносильное исходному.
Пример 1. 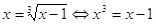
Теорема 4. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное исходному.
Пример 1. 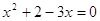
Теорема 5. Если обе части уравнения умножить или разделить на одно и тоже отличное от ноля число, то получится уравнение, равносильное исходному.
Пример 1. 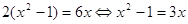
Теорема 6. Если в какой либо части уравнения выполнить тождественные преобразования, не меняющие области определения уравнения, то получится уравнение, равносильное исходному.
В школьной практике при решении иррациональных уравнений чаще всего используются два основных метода:
1) обеих частей уравнения в одну и ту же степень;
2) введение новых (вспомогательных) переменных.
Эти методы будем считать стандартными. В обязательном школьном курсе обычно этими методами и ограничиваются. Однако иногда приходится применять нестандартные методы и искусственные приемы решения иррациональных уравнений.
Типичная ошибка при решении иррациональных уравнений состоит в том, что школьники без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению «посторонних» корней.
При возведении обеих частей иррационального уравнения в одну и ту же степень надо иметь в виду, что если степень — не четное число, то получим равносильное уравнение, если же степень — четное число, то получим уравнение — следствие. Поэтому при решении иррациональных уравнений в большинстве случаев необходима проверка найденных решений.
Проверки можно избежать, если решать иррациональные уравнения с помощью равносильных замен. Для этого полезно знать следующие теоремы.
Теорема 7. Уравнение вида 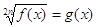
Уравнение вида
Теорема 8. Уравнение вида 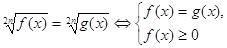
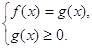
Уравнение вида 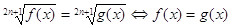
Далее рассмотрим более подробно типы иррациональных уравнений и методы их решения.
- Как решать квадратные уравнения
- Понятие квадратного уравнения
- Приведенные и неприведенные квадратные уравнения
- Полные и неполные квадратные уравнения
- Решение неполных квадратных уравнений
- Как решить уравнение ax 2 = 0
- Как решить уравнение ax 2 + с = 0
- Как решить уравнение ax 2 + bx = 0
- Как разложить квадратное уравнение
- Дискриминант: формула корней квадратного уравнения
- Алгоритм решения квадратных уравнений по формулам корней
- Примеры решения квадратных уравнений
- Формула корней для четных вторых коэффициентов
- Формула Виета
- Упрощаем вид квадратных уравнений
- Связь между корнями и коэффициентами
- Метод возведения обеих частей уравнения в одну и ту же степень
- Для решения каких уравнений применяется
- В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
- Обоснование метода
- Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
- Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
- 📹 Видео
Видео:Лучший метод возведения в квадрат любого числаСкачать
Как решать квадратные уравнения
О чем эта статья:
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:Математика| Разложение квадратного трехчлена на множители.Скачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать  Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать  Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Видео:✓ Как возводить в иррациональную степень | Ботай со мной #017 | Борис ТрушинСкачать  Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать  Метод возведения обеих частей уравнения в одну и ту же степеньПродолжаем изучать методы решения уравнений. Сейчас мы в деталях разберем метод возведения обеих частей уравнения в одну и ту же степень. Начнем с теории: рассмотрим, для решения каких уравнений применяется метод, опишем, в чем он состоит, приведем теоретическое обоснование метода возведения обеих частей уравнения в одну и ту же степень, запишем соответствующие алгоритмы решения уравнений. После этого сосредоточимся на практике и рассмотрим разнообразные примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень. Видео:Понятие модуля | Возведение уравнения в квадратСкачать  Для решения каких уравнений применяетсяМетод возведения обеих частей уравнения в одну и ту же степень в первую очередь применяется для решения иррациональных уравнений. Это объясняется тем, что возведение в натуральную и большую единицы степень позволяет избавляться от корней. Например, возведение в степень позволяет избавляться от корней при решении следующих уравнений:
Метод возведения обеих частей уравнения в одну и ту же степень используется и для решения некоторых уравнений, в которых переменная находится в основаниях степеней с дробными показателями. Например, уравнение Также метод возведения частей уравнения в степень применяется при решении некоторых степенных уравнений, в которых фигурируют иррациональные показатели. В пример приведем два уравнения Видео:Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать  В чем состоит метод возведения обеих частей уравнения в одну и ту же степеньМетод состоит в переходе к уравнению, которое получается из исходного путем возведения его обеих частей в одну и ту же степень, и нахождении решения исходного уравнения по решению полученного уравнения. На практике наиболее часто прибегают к возведению обеих частей уравнения в одну и ту же натуральную степень, большую единицы, то есть, в квадрат, куб и т.д. Делается это на базе следующего утверждения: Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень, большую единицы, дает равносильное уравнение (см. равносильные уравнения и уравнения-следствия). Реже приходится обращаться к возведению обеих частей уравнения в другие степени, в частности, в дробные рациональные и иррациональные. В этих случаях отталкиваются от такого утверждения: Уравнение A(x)=B(x) , на области допустимых значений переменной x для которого A(x)>0 или A(x)≥0 , B(x)>0 или B(x)≥0 , равносильно уравнению A r (x)=B r (x) , где r – положительное действительное число. Видео:Как решить уравнение - возведение в квадрат | Профильная МатематикаСкачать  Обоснование методаОбоснованием метода возведения обеих частей уравнения в одну и ту же степень является доказательство утверждений из предыдущего пункта. Приведем эти доказательства. Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение. Докажем его для уравнений с одной переменной. Для уравнений с несколькими переменными принципы доказательства те же. Пусть A(x)=B(x) – исходное уравнение и x0 – его корень. Так как x0 является корнем этого уравнения, то A(x0)=B(x0) – верное числовое равенство. Мы знаем такое свойство числовых равенств: почленное умножение верных числовых равенств дает верное числовое равенство. Умножим почленно 2·k , где k – натуральное число, верных числовых равенств A(x0)=B(x0) , это нам даст верное числовое равенство A 2·k (x0)=B 2·k (x0) . А полученное равенство означает, что x0 является корнем уравнения A 2·k (x)=B 2·k (x) , которое получено из исходного уравнения путем возведения его обеих частей в одну и ту же четную натуральную степень 2·k . Для обоснования возможности существования корня уравнения A 2·k (x)=B 2·k (x) , который не является корнем исходного уравнения A(x)=B(x) , достаточно привести пример. Рассмотрим иррациональное уравнение Так доказано, что возведение обеих частей уравнения в одну и ту же четную натуральную степень приводит к уравнению-следствию. Остается доказать, что возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение. Покажем, что каждый корень уравнения является корнем уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, и обратно, что каждый корень уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, является корнем исходного уравнения. Пусть перед нами уравнение A(x)=B(x) . Пусть x0 – его корень. Тогда является верным числовое равенство A(x0)=B(x0) . Изучая свойства верных числовых равенств, мы узнали, что верные числовые равенства можно почленно умножать. Почленно умножив 2·k+1 , где k – натуральное число, верных числовых равенств A(x0)=B(x0) получим верное числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) , которое означает, что x0 является корнем уравнения A 2·k+1 (x)=B 2·k+1 (x) . Теперь обратно. Пусть x0 – корень уравнения A 2·k+1 (x)=B 2·k+1 (x) . Значит числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) — верное. В силу существования корня нечетной степени из любого действительного числа и его единственности будет верным и равенство Так доказано, что возведение обеих частей иррационального уравнения в нечетную степень дает равносильное уравнение. Доказанное утверждение пополняет известный нам арсенал, использующийся для решения уравнений, еще одним преобразованием уравнений – возведением обеих частей уравнения в одну и ту же натуральную степень. Возведение в одну и ту же четную степень обеих частей уравнения является преобразованием, приводящим к уравнению-следствию, а возведение в нечетную степень – равносильным преобразованием. На этом преобразовании базируется метод возведения обеих частей уравнения в одну и ту же степень. Утверждение, касающееся возведения обеих частей уравнения в одну и ту же положительную действительную степень, доказывается аналогично с опорой на единственность степени положительного числа с действительным показателем. Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать  Алгоритмы решения уравнений методом возведения частей в одну и ту же степеньЕсть смысл записать три алгоритма решения уравнений методом возведения обеих частей уравнения в одну и ту же степень: первый – для возведения в нечетную степень, второй – для возведения в четную степень, третий – для возведения в ненатуральную положительную степень. Алгоритм решения уравнений методом возведения обеих частей в одну и ту же нечетную степень:
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же четную степень:
Обратите внимание: этот алгоритм, в отличие от предыдущего, содержит пункт, касающийся отсеивания посторонних корней. Это связано с тем, что возведение обеих частей уравнения в одну и ту же нечетную степень приводит к равносильному уравнению, а возведение обеих частей уравнения в четную степень в общем случае приводит к уравнению-следствию. Поэтому, в результате возведения в нечетную степень посторонние корни не возникают, а при возведении в четную степень посторонние корни могут появиться. Таким образом, при возведении частей уравнения в четную степень возникает необходимость в отсеивании посторонних корней. Почему отсеивание посторонних корней в этом случае нужно проводить методом, не использующим ОДЗ? Потому что возведение обеих частей уравнения в четную степень может приводить к появлению посторонних корней в пределах ОДЗ, и отсеять их по ОДЗ или по условиям ОДЗ невозможно. Наконец, запишем алгоритм решения уравнений методом возведения обеих частей в одну и ту же положительную дробную рациональную или иррациональную степень:
Видео:Возведение в квадратСкачать  Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степеньБольшое количество попадающих под разбираемую тему примеров с подробными решениями приведено в статье решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. В добавление к этим примерам стоит разобрать решение уравнения через возведение обеих частей уравнения в одну и ту же степень, не являющуюся натуральным числом. Решите уравнение Решать заданное уравнение можно несколькими разными методами. Например, можно провести решение методом логарифмирования. Также можно преобразовать уравнение к виду Учитывая свойство степени в степени (см. свойства степеней), несложно догадаться, что избавиться от иррациональных показателей позволяет возведение обеих частей уравнения в степень Итак, проводим возведение обеих частей уравнения Решаем полученное уравнение: Так мы пришли к кубическому уравнению x 3 −x 2 +2=0 . Один его корень x=−1 легко подбирается. Разделив многочлен x 3 −x 2 +2 на двучлен x+1 , получаем возможность представить кубическое уравнение в виде (x+1)·(x 2 −2·x+2)=0 . Квадратное уравнение x 2 −2·x+2=0 не имеет решений, так как его дискриминант отрицательный. Из этого заключаем, что уравнение x 3 −x 2 +2=0 имеет единственный корень x=−1 . В процессе решения мы дважды отмечали, что нам будет необходимо сделать проверку найденных корней. Сейчас пришло это время. Проверку выполним через подстановку найденного корня x=−1 в исходное уравнение 📹 ВидеоПолный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать  Уникальный метод возведения в квадрат для детейСкачать  Возведение в степень произведения и степени. Алгебра, 7 классСкачать  Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  Как быстро возводить в квадрат – 3 лучших способа // Vital MathСкачать  Как решают уравнения в России и СШАСкачать  |
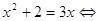
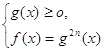
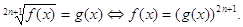








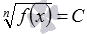 , C≥0 , в частности,
, C≥0 , в частности,  ,
,  и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению 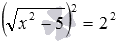 , и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению 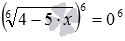 и дальше — к элементарному уравнению 4−5·x=0 .
и дальше — к элементарному уравнению 4−5·x=0 .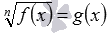 , например,
, например,  ,
,  и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.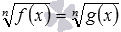 и
и  , таких как
, таких как 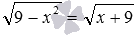 ,
, 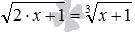 и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень. и
и  . В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала. . Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза. можно решить методом возведения его обеих частей в дробную степень 6/11 .
можно решить методом возведения его обеих частей в дробную степень 6/11 . и
и  . Возведение их обеих частей в одну и ту же степень (в первом случае в степень
. Возведение их обеих частей в одну и ту же степень (в первом случае в степень  , во втором – в степень
, во втором – в степень  ) позволяет избавиться от степеней с иррациональными показателями и перейти к сравнительно простым уравнениям.
) позволяет избавиться от степеней с иррациональными показателями и перейти к сравнительно простым уравнениям. , и уравнение
, и уравнение  , которое получено из исходного путем возведением его обеих частей в квадрат. Несложно проверить, что нуль является корнем уравнения
, которое получено из исходного путем возведением его обеих частей в квадрат. Несложно проверить, что нуль является корнем уравнения  , что то же самое 4=4 — верное равенство. Но при этом нуль является посторонним корнем для уравнения
, что то же самое 4=4 — верное равенство. Но при этом нуль является посторонним корнем для уравнения  , что то же самое 2=−2 , которое неверное. Этим доказано, что уравнение, полученное из исходного путем возведения его обеих частей в одну и ту же четную степень, может иметь корни, посторонние для исходного уравнения.
, что то же самое 2=−2 , которое неверное. Этим доказано, что уравнение, полученное из исходного путем возведения его обеих частей в одну и ту же четную степень, может иметь корни, посторонние для исходного уравнения. . Оно в свою очередь в силу тождества
. Оно в свою очередь в силу тождества  , где a – любое действительное число, которое следует из свойств корней и степеней, может быть переписано как A(x0)=B(x0) . А это означает, что x0 является корнем уравнения A(x)=B(x) .
, где a – любое действительное число, которое следует из свойств корней и степеней, может быть переписано как A(x0)=B(x0) . А это означает, что x0 является корнем уравнения A(x)=B(x) . и перейти к уравнению
и перейти к уравнению  на основании метода освобождения от внешней функции, или, сославшись на единственность степени с данным основанием и данным показателем. Но в рамках текущей статьи нас интересует решение уравнения методом возведения его обеих частей в одну и ту же степень, поэтому, проведем решение именно этим методом.
на основании метода освобождения от внешней функции, или, сославшись на единственность степени с данным основанием и данным показателем. Но в рамках текущей статьи нас интересует решение уравнения методом возведения его обеих частей в одну и ту же степень, поэтому, проведем решение именно этим методом. . Здесь мимоходом заметим, что
. Здесь мимоходом заметим, что  . Это уравнение равносильно исходному, значит, решив его, мы будем иметь интересующее нас решение.
. Это уравнение равносильно исходному, значит, решив его, мы будем иметь интересующее нас решение.
