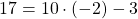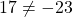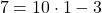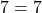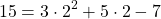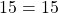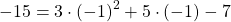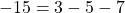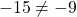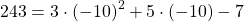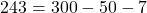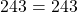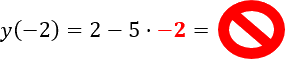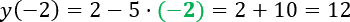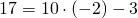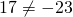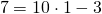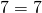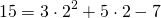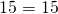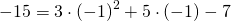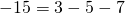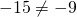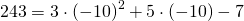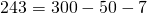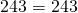Когда точка принадлежит графику уравнения (7 видео)

Принадлежит ли графику функции точка

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.

Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.

Ответ: точки A и C принадлежат графику функции.

Содержание

График линейной функции, его свойства и формулы
Понятие функции
Понятие линейной функции
Свойства линейной функции
Построение линейной функции
Решение задач на линейную функцию
Как определить принадлежит ли точка графику функции
Как получить значение функции
Как проверить верно ли равенство для функции
Неправильно
Правильно
Как проверить, что точка принадлежит графику функции
Как получить координаты точки функции
Ответ
Проверено экспертом
🔍 Видео

Видео:8 класс. График функции. Принадлежит ли точка графику функции. Как узнать?Скачать

График линейной функции, его свойства и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Определить, принадлежит ли точка с заданными координатами графику функцииСкачать

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0;
и т. д.

Для удобства результаты можно оформлять в виде таблицы:

х	0	2	4
y	-2	-1	0

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Свойства линейной функции

Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b).
x=-b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, — b /_k) и положительные значения на промежутке (- b /_k, +∞)
При k b /_k, +∞) и положительные значения на промежутке (-∞, — b /_k).
Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k

Видео:7 кл.Принадлежит ли графику функции 3x+4y=12 точка А(4;1)Скачать

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = — b /_k.
Координаты точки пересечения с осью OX: (- b /_k; 0)

Видео:Вариант 72, № 2. Выбрать точку, принадлежащую графику уравнения ax+by=cСкачать

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.

Видео:Принадлежит ли точка графику функции. Алгебра 7 классСкачать

Как определить принадлежит ли точка графику функции

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Видео:Как построить график линейной функции.Скачать

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

Вычислить « y » при « x = 15 »
Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный .

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.

Теперь разделим и левую, и правую часть на « 2 », чтобы найти « x » .

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Как проверить верно ли равенство для функции

Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».

Верно ли равенство « f(−2) = −18 »?

Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.

Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.

Не забывайте использовать правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили « f(−2) = 12 ».

Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию « y = x 2 −5x + 6 »

Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2) .

Для этой задачи нет необходимости, строить график заданной функции.

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).

Если получится верное равенство , значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию « y = x 2 − 5x + 6 » координаты точки (1; 2) .

Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».

У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1) . Принадлежит ли она
функции « y = x 2 − 5x + 6 »?

Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».

В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »

Видео:Определим,проходит ли график через данную точку.Скачать

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.

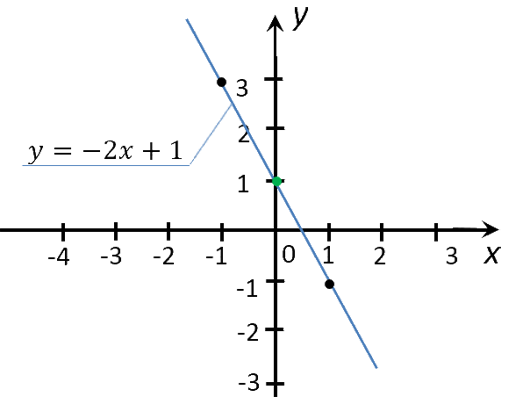
Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.

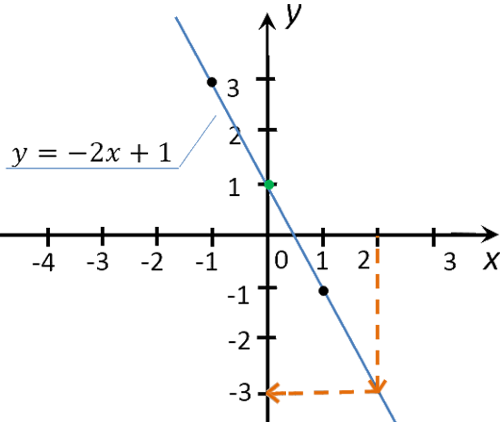
Найдем на графике функции « y(x) = −2x + 1 », чему равен « y » при x = 2 .

Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».

Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».

Для этого мы подставим x = 2 в формулу функции « y(x) = −2x + 1 ». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3 .

При расчетах мы также получили y = −3 .

Значит, мы правильно получили координаты с графика функции.

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.

При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Ответ: точки A и C принадлежат графику функции.

Как определить принадлежит ли графику функции точка? (Составить алгоритм)

Попроси больше объяснений
Следить
Отметить нарушение

Видео:Как проверить, принадлежит ли точка с заданными координатами графику данной функцииСкачать

Ответ

Проверено экспертом

Подставить в уравнение графика координаты точки. Если уравнение обратится в тождество, значит, точка принадлежит графику, если нет, то не принадлежит.

Подставим координаты точки А: 5 = 3 + 2; 5=5 – тождество, значит, точка принадлежит графику.
Подставим координаты точки В: 8 = -1+2; 8=1 – не тождество, значит, точка не принадлежит графику.