Когда система уравнений не имеет решений матрицы

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Когда система уравнений не имеет решений матрицы

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Видео:При каких λ однородная система уравнений имеет ненулевое решение?Скачать

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Системы линейных уравнений

Обозначим через $ mathbb A_ $ любое из множеств $ mathbb Q_, mathbb R_ $ или $ mathbb C_ $.

Примеры систем уравнений над $ mathbb R $.

Относительно числа $ m_ $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_ $. Если $ m_>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=alpha_,dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.

Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:

1. система совместна и имеет единственное решение;

2. cистема совместна и имеет бесконечное множество решений;

3. cистема несовместна.

При этом все решения будут находиться в том же множестве $ mathbb A_ $, что и коэффициенты системы.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Матричная форма записи

Для системы линейных уравнений относительно переменных $ x_1,x_2,dots,x_n $ $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_2,\ dots & & & & dots \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_m. end right. $$ матрицей системы называется матрица $$ A=left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)_ ; $$ cтолбец $$ = left( begin b_ \ b_ \ vdots \ b_ end right) $$ называется столбцом правых частей системы, а столбец $$ X= left( begin x_ \ x_ \ vdots \ x_ end right) $$ — столбцом неизвестных. Используя правило умножения матриц, систему можно записать в матричном виде: $$ AX= . $$ Любое решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы можно также записать в виде столбца: $$ X=left( begin alpha_1 \ vdots \ alpha_n end right) in mathbb A^n . $$ Матрица, составленная из всех коэффициентов системы уравнений: $$ [A mid mathcal B ]= left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ , $$ т.е. конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ называется расширенной матрицей системы л.у.

Видео:Матричный метод решения систем уравненийСкачать

Исключение переменных (метод Гаусса)

метода достаточно проста.

Пример. Решить систему уравнений $$ left< begin 2x_1&-3x_2&-x_3&=3 \ 4x_1&-3x_2&-5x_3&=6 \ 3x_1&+5x_2&+9x_3&=-8 end right. $$

Решение. Выразим из первого уравнения $ x_ $ $$ x_1=frac x_2+frac x_3 + frac $$ и подставим в оставшиеся уравнения $$ 4 left(frac x_2+frac x_3 + fracright) -3,x_2-5,x_3=6 <coloriff > 3x_2-3x_3 = 0 $$ $$ <coloriff > x_2-x_3=0 ; $$ $$ 3 left(frac x_2+frac x_3 + fracright) +5x_2+9x_3=-8 <coloriff > frac x_2 +fracx_3=-frac $$ $$ <coloriff > 19x_2 +21x_3=-25 . $$ Два получившихся уравнения не зависят от неизвестной $ x_ $ — она оказалась исключенной из этих уравнений. Иными словами, мы получили новую подсистему уравнений $$ left< begin x_2&-x_3&=0 \ 19x_2&+21x_3&=-25, end right. $$ которой должны удовлетворять неизвестные $ x_ $ и $ x_ $. Продолжаем действовать по аналогии: выразим из первого уравнения $ x_ $ через $ x_ $: $$x_2=x_3 $$ и подставим во второе: $$ 40 x_3 =-25 iff x_3=-frac . $$ Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение $ x_ $ в полученные по ходу решения соотношения: $$ x_2=x_3=-frac Rightarrow x_1=frac x_2+frac x_3 + frac=frac . $$

Ответ. $ x_=1/4, x_2=-5/8, x_3=-5/8 $.

Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.

Исключение переменных

Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:

1. перестановка двух уравнений;

2. умножение обеих частей уравнения на любое отличное от нуля число;

3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ begin a_x_1 +a_x_2+ ldots+a_x_n &=&b_j,\ a_x_1 +a_x_2+ ldots+a_x_n &=&b_k end $$ заменяется парой $$ begin (a_+ <colorlambda > a_) x_1 &+ (a_+ <colorlambda > a_) x_2 &+ ldots &+ (a_+ <colorlambda > a_) x_n &=&b_j + <colorlambda > b_k, , \ a_x_1 &+a_x_2&+ ldots &+a_x_n &=&b_k , . end $$

Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.

Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.

Предположим, что первое уравнение системы содержит явно неизвестную $ x_ $, т.е. $ a_^ ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_/a_^ $. Получим $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_2 — frac<a_><a_> b_1 , $$ Аналогичное преобразование — вычитание из третьего уравнения системы первого, умноженного на $ a_/a_^ $, позволяет исключить $ x_ $ из этого уравнения, т.е. заменить его на $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_3 — frac<a_><a_> b_1 . $$ Продолжаем процесс далее. В конечном итоге исключаем $ x_ $ из всех уравнений кроме первого: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ &a_^x_2&+ ldots&+a_^x_n &=b_2^,\ &dots & & & dots \ &a_^x_2&+ ldots&+a_^x_n &=b_m^. end right. npu begin a_^ &= & displaystyle a_ — frac<a_a_><a_> ,\ b_j^ &= & displaystyle b_j — frac<a_b_1><a_> . end $$ Полученная система эквивалентна исходной системе, однако она имеет более простой вид: в ней выделилась подсиcтема $$ left< begin a_^x_2&+ ldots&+a_^x_n &=b_2^,\ dots & & & dots \ a_^x_2&+ ldots&+a_^x_n &=b_m^, end right. $$ которая не зависит от переменной $ x_ $. К этой новой подсистеме можно применить те же рассуждения, что и к исходной системе, поставив теперь целью исключение переменной $ x_ $.

Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ ell_ $-я подсистема имеет коэффициент $ a_^ $ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_^ $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_^ $ был бы равен нулю). Возможные варианты дальнейших действий:

1. если хотя бы один коэффициент при $ x_^ $ в одном из оставшихся уравнений отличен от нуля: $ a_^ne 0^ $, то это уравнение переставляется с $ ell_ $-м;

2. если при всех $ jge ell^ $ коэффициенты $ a_^ $ равны нулю, то переменная $ x_^ $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_^ $.

Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ left< begin a_x_1 +&a_x_2&+ ldots& +a_<1 >x_& +a_ <1 ,+1>x_<+1>&+ ldots + & a_x_n &=b_1,\ &a_^x_2&+ ldots& +a_<2 >^ x_& +a_<2 ,+1>^ x_<+1>&+ ldots + & a_^ x_n &=b_2^,\ & & ddots & & & & & dots \ & & & a_ <>^<[-1]>x_ & + a_ <, +1>^<[-1]>x_<+1>& + ldots + & a_ <,n>^<[-1]>x_n &=b_^<[-1]>, \ & & & & & & 0 &=b_<+1>^<[-1]>, \ & & & & & & dots & \ & & & & & & 0 &=b_^<[-1]>, \ end right. $$ при $ le n_ $. Заметим, что все коэффициенты этой системы будут принадлежать тому же множеству, что и коэффициенты исходной системы.

Предположение . Мы будем считать, что каждое из первых $ _ $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.

Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.

Исторический комментарий о Гауссе ☞ ЗДЕСЬ.

Установление множества решений

Теорема. Если хотя бы одно из чисел $ b_<+1>^<[-1]>,dots , b_^<[-1]> $ отлично от нуля, то исходная система линейных уравнений будет несовместной.

Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ mathbb R_ $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ to_ $.

Пример. Решить систему л.у.

$$ left< begin x_1&+x_2&-3, x_3 =& -1 \ 2,x_1&+x_2&-2, x_3 =& 1 \ x_1&+x_2&+ x_3 =& 3 \ x_1&+2,x_2&-3, x_3 =& 1. end right. $$

Решение. $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &x_2&=& 2 end right. to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&4, x_3=& 5 end right. to $$ $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&0=& 1 end right. $$ Последнее равенство абсолютно противоречиво.

Ответ. Система несовместна.

Пусть теперь $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $. Возможны два случая: $ =n_ $ и $ предположения , имеем $ a_^ ne 0 $. Но тогда, поскольку система является конечной стадией прямого хода метода Гаусса, то и все коэффициенты $ a_^, dots, a_^, a_ $ должны быть отличны от нуля — в противном случае метод Гаусса не остановился бы на системе такого вида; он называется треугольным: Из последнего уравнения системы можно однозначно установить значение $ x_ $: $$x_n=b_n^ big/ a_^ .$$ Далее, подставляя это значение в $ (n-1) $-е уравнение системы, выражаем $ x_ $: $$ x_= frac<b_^ — a_^x_>< a_^>= frac< b_^ — a_^ b_n^ Big/ a_^>< a_^> . $$ Подставляем полученные значения для $ x_ $ и $ x_ $ в $ (n-2)_ $-е уравнение системы, выражаем $ x_ $, и т.д., в конце концов приходим к первому уравнению, из которого выражаем $ x_ $ если ранее уже получены выражения для $ x_2,dots,x_ $.

Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ mathfrak r = n_ $ и $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $, то исходная система линейных уравнений имеет единственное решение.

Пример. Решить систему л.у.

$$ left< begin x_1&+3,x_2&+ x_3 =&5 \ 2,x_1&+x_2&+ x_3 =& 2 \ x_1&+x_2&+ 5,x_3 =& -7 \ 2,x_1&+3,x_2&-3, x_3 =& 14. end right. $$

Ответ. $ x_1=1,, x_=2,, x_3=-2 $ .

Исследуем теперь случай $ 1) : На основании предположения , в $ $-м уравнении этой системы имеется хотя бы один ненулевой коэффициент в левой части, пусть $ a_ <>^<[-1]>ne 0 $ — первый из них. Если $ =n $, то из этого уравнения однозначно определится $ x_ $ $$ x_n=alpha_n = b_^<[-1]> big/ a_ <n>^<[-1]> . $$ Если же $ предположения , в этом уравнении имеется хотя бы один ненулевой коэффициент в левой части; пусть $ a_<-1, >^<[-2]>ne 0_ $ — первый из них. Поскольку мы преположили, что система является конечной стадией прямого хода метода Гаусса, то $ по крайней мере две переменные, значения которых еще не были зафиксированы на предыдущих шагах. Это следует из предположения, что число уравнений $ _ $ меньше числа неизвестных $ n_ $. Такое уравнение допускает бесконечное число решений, любое из которых в ходе дальнейших шагов может быть «доделано» до решения системы.

Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ mathfrak r 2) матрицы $ A_ $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.

Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Формулы Крамера

Рассмотрим систему линейных уравнений с квадратной матрицей $ A_ $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.

Теорема. Cистема

$$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_n endright. $$ имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $$ left| begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 . $$ В этом случае решение можно вычислить по формулами Крамера 3) : $$ x_k =frac<det left[ A_|dots|A_||A_|dots|A_ right]> quad npu quad kin . $$ Для получения значения $ x_ $ в числитель ставится определитель, получающийся из $ det A_ $ заменой его $ k_ $-го столбца на столбец правых частей ( здесь $ | $ означает конкатенацию).

Доказательство ☞ ЗДЕСЬ

Пример. Решить систему уравнений

$$ left<begin 2x_1& +3x_2&+11x_3&+5x_4 &=& color2,\ x_1& +x_2&+5x_3&+2x_4 &=& color1 ,\ 2x_1& +x_2&+3x_3&+2x_4 &=&color,\ x_1& +x_2&+3x_3&+4x_4 &=&color. endright. $$

Решение. $$ x_1=frac<left|begin color2 & 3&11&5 \ color1 & 1&5&2 \ color& 1&3&2 \ color & 1&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=-2, x_2=frac<left|begin 2& color2&11&5 \ 1& color1&5&2 \ 2& color&3&2 \ 1& color&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=0, dots $$ Найдите оставшиеся компоненты решения. ♦

Решение системы линейных уравнений с квадратной матрицей $ A_ $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_ ne 0 $.

Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.

Еще один способ решения системы основан на построении обратной матрицы: $$ AX= quad Rightarrow quad X=A^ . $$ Этот способ малоэффективен при фиксированных числовых $ A_ $ и $ _ $.

Найти достаточное условие существования общего решения систем уравнений:

$$ A_1 X = _1 quad u quad A_2 Y = _2 , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.

Видео:Система уравнений не имеет решений | Системы уравнений | Алгебра 1Скачать

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ $$ [ A| ] = left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ $$ называется расширенной матрицей системы линейных уравнений $ AX= $.

Теорема [Кронекер, Капелли]. Система $ AX= $ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

$$ operatorname, A = operatorname, [ A| ] . $$ При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_ $ совпадает с общим значением ранга $ mathfrak r_ $, и бесконечное множество решений, если $ n_ $ больше этого значения.

Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы, тогда $$alpha_1 A_+dots+alpha_n A_= ,$$ т.е. столбец $ $ линейно выражается через столбцы $ A_,dots,A_ $. Но тогда $$ operatorname <A_,dots,A_>=operatorname <A_,dots,A_,> .$$ Следовательно $ operatorname, A = operatorname, [ A| ] $.

Доказательство достаточности проводится в следующем пункте. ♦

Пример. Исследовать совместность системы уравнений

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ det A_ $. Если он отличен от нуля — система совместна. $$det A = left| begin<color> &1&1&1 \ 1&<color>&1&1 \ 1&1&<color>&1 \ 1&1&1&<color> end right|= left| begin (<color>-1) &(1-<color>)&0&0 \ 0&(<color>-1)&(1-<color>)&0 \ 0&0&(<color>-1)&(1-<color>) \ 1&1&1&<color> end right| =(<color>-1)^3 left| begin 1 &-1&0&0 \ 0&1&-1&0 \ 0&0&1&-1 \ 1&1&1&<color> end right|= $$ $ =(<color>-1)^3(<color>+3) $. По теореме Крамера при $ <color>ne 1 $ и при $ <color>ne -3 $ решение системы единственно: $$x_1=x_2=x_3=x_4=1/(<color>+3) .$$

Осталось исследовать критические случаи: $ <color>=1_ $ и $ <color>= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При $ <color>= 1_ $ имеем $$ operatorname left( begin 1 &1&1&1 \ 1&1&1&1 \ 1&1&1&1 \ 1&1&1&1 end right)= operatorname left( begin 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 end right)=1 , $$ и система совместна. Она эквивалентна единственному уравнению $$x_1+x_2+x_3+x_4=1 ,$$ которое имеет бесконечно много решений.

При $ <color>= -3 $: $$ operatorname left( begin -3 &1&1&1 \ 1&-3&1&1 \ 1&1&-3&1 \ 1&1&1&-3 end right)=3,quad operatorname left( begin -3 &1&1&1&1 \ 1&-3&1&1&1 \ 1&1&-3&1&1 \ 1&1&1&-3&1 end right)=4 $$ и система несовместна.

Ответ. Система несовместна при $ <color> = -3 $; она имеет бесконечное множество решений при $ <color> = 1_ $ и единственное решение при $ <color> notin $.

Система однородных уравнений

$$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0 end right. $$ всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_) $ лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_ $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ left< begin ax_1+by_1+c & =0\ ax_2+by_2+c & =0\ ax_3+by_3+c & =0 end right. $$ Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_ $ при хотя бы одном из чисел отличном от нуля): $$ left|begin x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 & 1 end right|=0 . $$ ♦

Доказать, что для совместности системы

$$ left< begin a_x_1+a_x_2+a_x_3 &=& b_1 \ a_x_1+a_x_2+a_x_3 &=& b_2 \ a_x_1+a_x_2+a_x_3 &=& b_3 \ a_x_1+a_x_2+a_x_3 &=& b_4 end right. $$ необходимо, чтобы было выполнено условие $$ left| begin a_&a_& a_ & b_1 \ a_&a_& a_ & b_2 \ a_&a_& a_ & b_3 \ a_&a_& a_ & b_4 end right|=0 quad . $$ Является ли это условие достаточным для совместности?

An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система $ n_ $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.

Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.

Ответ ☞ ЗДЕСЬ

Видео:Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать

Общее решение

Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname (A)=operatorname[Amid mathcal B ] =mathfrak $. По определению ранга матрицы, в матрице $ A $ существует минор порядка $ mathfrak $, отличный от нуля; этот же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы 4) : $$ Delta = Aleft( begin 1 & 2 & dots & mathfrak \ 1 & 2 & dots & mathfrak end right) = left| begin a_ & a_ & dots & a_<1mathfrak> \ a_ & a_ & dots & a_<2mathfrak> \ dots &&& dots \ a_<mathfrak1> & a_<mathfrak2> & dots & a_ <mathfrakmathfrak> end right| ne 0 . $$ Тогда первые $ mathfrak $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak $ уравнений системы на соответствующие числа и складывая их, получим любое оставшееся уравнение. Таким образом, система уравнений может быть заменена эквивалентной ей системой из первых $ mathfrak $ уравнений: $$ left< begin a_x_1+dots+a_<1mathfrak>x_<mathfrak>&+a_<1,mathfrak+1>x_<mathfrak+1>+ dots +a_x_n&=&b_1, \ dots & & & dots \ a_<mathfrak1>x_1+dots+a_<mathfrakmathfrak>x_<mathfrak>& +a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n&=&b_mathfrak end right. quad iff quad A^ X=^ $$ Если $ mathfrak=n $, то матрица $ A^ $ квадратная. По предположению $ det A^ ne 0 $. По теореме Крамера решение такой системы единственно.

Пусть теперь $ mathfrak произвольных фиксированных значениях $ x_<mathfrak+1>,dots,x_n $: $$ x_j=frac< left| begin a_ & dots &a_ &left[ b_1-(a_<1,mathfrak+1>x_<mathfrak+1>+dots +a_x_n) right] &a_& dots &a_<1mathfrak> \ dots &&&dots&&& dots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & left[ b_<mathfrak>- (a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n) right] &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| > $$ $$ mbox jin <1,dots, mathfrak> . $$ Таким образом, в этом случае система имеет бесконечное множество решений. Используя свойство линейности определителя по столбцу (см. свойство 5 ☞ ЗДЕСЬ ), формулы можно переписать в виде $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Здесь $$ beta_j =frac left| begin a_ & dots &a_ & b_1 &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & b_<mathfrak> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right|, , $$ $$ gamma_ = -frac left| begin a_ & dots &a_ & a_ &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & a_<mathfrakk> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| . $$ Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них переменные $ x_<mathfrak+1>,dots,x_n $ называются основными (или свободными), а $ x_1,dots,x_<mathfrak> $ — зависимыми. Решение, получающееся из общего решения фиксированием значений основных переменных, называется частным решением системы уравнений.

Пример. Исследовать совместность и найти общее решение системы уравнений:

Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| ne 0,quad left| begin 2 & 1 \ 6 & 2 end right| ne 0, quad left| begin 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end right|=2 ne 0 , $$ а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname (A) =3 $. Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить окаймление найденного ненулевого минора третьего порядка с помощью элементов взятых из столбца правых частей. Имеется всего один такой минор, и он равен нулю. Следовательно $ operatorname[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.

Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ begin x_1&=&frac<left| begin 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1 end right|> -x_2frac<left| begin -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1 end right|> -x_5frac<left| begin 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1 end right|> =-frac+fracx_2+fracx_5, \ & & \ x_3&=&frac<left| begin 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1 end right|> -x_5frac<left| begin 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1 end right|>=3-4x_5, \ & & \ x_4 &=&frac<left| begin 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2 end right|> -x_5frac<left| begin 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2 end right|> = 0. end $$ Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений: $$ left< begin 2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \ &&x_3&+2x_4&+4x_5&=&3, \ &&&x_4&&=&0 end right. $$ Используя обратный ход метода Гаусса, снова приходим к полученным формулам.

Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.

Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_<mathfrak+1>=0,dots,x_n=0 $. Величины же коэффициентов $ gamma_ $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если $ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$

Вывод. Формула общего решения системы $ A X=mathcal B $: $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> $$ состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы: $$ x_1= beta_1,dots, x_<mathfrak>= beta_<mathfrak>,x_<mathfrak+1>=0,dots,x_n=0 ; $$ оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $. ♦

Теперь посмотрим как можно описать общее решение однородной системы.

Система однородных уравнений

Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0. end right. $$ или, в матричном виде: $$ A_X=_ $$

Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_ $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ det (A_) = 0 $ является и достаточным для существования нетривиального решения.

Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_ $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_) = 0 $.

Для произвольной (не обязательно квадратной) матрицы $ A_ $ имеет место следующий общий результат.

Теорема 2. Если $ operatorname (A)=mathfrak r 5) $ A_^ $.

Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^ $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.

Пусть матрица системы $ AX=mathbb O $ квадратная и

$$ operatorname (A) =n_-1 , .$$ Доказать, что если ненулевой минор матрицы порядка $ n_-1 $ соответствует какому-нибудь элементу $ j_ $-й строки, то система алгебраических дополнений к элементам $ a_,dots,a_^ $ этой строки составляет ФСР для $ AX=mathbb O_ $. Например, для системы $$ left< begin a_x_1 +a_x_2+a_x_3&=0,\ a_x_1 +a_x_2+a_x_3&=0 end right. $$ ФСР состоит из решения $$ x_1=left| begin a_ & a_ \ a_ & a_ end right| , x_2=-left| begin a_ & a_ \ a_ & a_ end right| , x_3=left| begin a_ & a_ \ a_ & a_ end right| , $$ если только хотя бы один из миноров отличен от нуля.

Теперь обсудим способы нахождения ФСР.

1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_,dots,x_ $, т.е. общее решение задается формулами $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Иными словами, вектор столбец $$ X=left(begin gamma_<1,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ gamma_<2,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ vdots \ gamma_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots+gamma_<mathfrakn>x_n \ x_<mathfrak+1> \ x_<mathfrak+2> \ vdots \ x_ endright) $$ будет решением однородной системы при любых наборах значений основных переменных $ x_<mathfrak+1>,dots,x_ $. Представим этот вектор в виде суммы векторов: $$ =x_<mathfrak+1> underbrace< left(begin gamma_<1,mathfrak+1> \ gamma_<2,mathfrak+1> \ vdots \ gamma_<mathfrak,mathfrak+1> \ 1 \ 0 \ vdots \ 0 endright)>_ + x_<mathfrak+2> underbrace<left(begin gamma_<1,mathfrak+2> \ gamma_<2,mathfrak+2> \ vdots \ gamma_<mathfrak,mathfrak+2> \ 0 \ 1 \ vdots \ 0 endright)>_+dots+ x_ underbrace<left(begin gamma_ \ gamma_ \ vdots \ gamma_<mathfrakn> \ 0 \ 0 \ vdots \ 1 endright)>_<X_> . $$ Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_- mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_ $ расположены на разных местах, и ни какая линейная комбинация столбцов $ < X_1,dots,X_> $ не сможет обратить их одновременно в нуль).

Оформим этот способ построения ФСР в теорему:

Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_ $ вида:

$$ A = left[ E_ mid P_ right] , $$ то ее ФСР состоит из столбцов матрицы $$ left[ begin — P^ \ hline E_ end right] . $$

Пример. Найти ФСР для системы уравнений

Решение. Приводим систему к трапециевидному виду: $$ left< begin x_1-&x_2+&x_3-&x_4=&0, \ &&x_3+&4x_4=&0 end right. $$ В качестве зависимых переменных можно взять, например, $ x_ $ и $ x_ $. $$ begin x_1 & x_3 & x_2 & x_4 \ hline 1 & 0 & 1 & 0 \ 5 & -4 & 0 & 1 end $$

2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_ $ системы и припишем к ней справа единичную матрицу порядка $ n_ $: $$ left[ A^ | E_n right] = left(begin a_ & a_ & dots & a_ & 1 & 0 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 1 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 0 & 1 & dots & 0 \ vdots & & & vdots & vdots & & & ddots & vdots \ a_ & a_ & dots & a_ & 0 & 0 & 0 & dots & 1 end right) ; $$ здесь $ |_ $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме: $$ left( begin hat A & K \ mathbb O & L end right) = left(begin color & * & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & color & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & 0 & color & dots & * & * & * & * & * & * & * & dots & * \ vdots & & & ddots & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & & 0 & color & * & * & * & * & * & dots & * \ hline 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \ vdots & & & & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box end right) begin left.begin \ \ \ \ \ endright> mathfrak r \ left. begin \ \ \ endright> n — mathfrak r end . $$ Элементы трапециевидной матрицы $ hat A $, обозначенные $ color $, могут быть равны нулю, но $ operatorname(hat A)= mathfrak r_ $. В этом случае строки матрицы $ L_ $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.

Пример. Найти ФСР для системы уравнений

$$ left< begin x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\ -3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\ x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\ -8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\ 6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0. end right. $$ Решение. Преобразуем матрицу $ left[ A^ | E_6 right] $

$$ left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 2 & -1 & 1 & -7 & 5 & & 1 \ 1 & 2 & 3 & 4 & 5 & & & 1 \ 3 & -4 & 2 & -15 & 11 &&&& 1 \ -1 & 1 & 1 & 6 & 0 &&&&& 1 \ 2 & -1 & 3 & -5 & 9 &&&&&& 1 end right)_ $$ к трапециевидной форме с помощью элементарных преобразований строк: $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \ 0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \ 0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \ 0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \ 0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \ 0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1 end right) $$

3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.

Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и $ operatorname (A) = $. Тогда характеристический полином матрицы $ A_ $ имеет вид:

Пример. Найти ФСР для системы уравнений

Решение. Здесь $$ A= left( begin 1 & 1 & -1 & -1 \ 2 & 3 & 1 & -2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1), $$ $$ A^2-4A+E= left( begin 0 & 0 & 4 & 1 \ 0 & 0 & -3 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 end right) $$

Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $ ☞ ЗДЕСЬ.

Видео:Исследование систем линейных уравнений на совместностьСкачать

Геометрическая интерпретация

Геометрический смысл введенных определений поясним на примере $ mathbb R^ $. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_ $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_ $ как функции $ x_2,x_3 $: $$ x_1=frac-fracx_2-fracx_3 . $$ В этом представлении переменные $ x_ $ и $ x_ $ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_ $ полностью определяется заданием $ x_ $ и $ x_ $. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_ $ и $ x_ $ выбраны основными, а $ x_ $ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами $$x_1=frac-fract-fracu, x_2=t, x_3=u quad npu quad subset mathbb R , $$ которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме: $$ left( begin x_1 \ x_2 \ x_3 end right)= left( begin b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u end right)= left( begin b/a_1\ 0 \ 0 end right)+ t left( begin -a_2/a_1\ 1 \ 0 end right) + u left( begin -a_3/a_1\ 0 \ 1 end right) . $$ Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое $$ X_0=left( begin b/a_1\ 0 \ 0 end right) $$ получается при задании $ t=0,u=0_ $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца $$ X_1=left( begin -a_2/a_1\ 1 \ 0 end right) quad u quad X_2=left( begin -a_3/a_1\ 0 \ 1 end right) $$ не задают решения нашего уравнения — если только $ bne 0_ $. Но оба удовлетворяют однородному уравнению $$ a_1x_1+a_2x_2+a_3x_3=0 , $$ Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор $ vec $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце ☞ ПУНКТА:

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Координаты произвольной точки плоскости $ a_1x_1+a_2x_2+a_3x_3=0 $ задаются соотношениями $$ left( begin x_1 \ x_2 \ x_3 end right)=tX_1+uX_2 . $$ Векторы пространства $ vec $ и $ vec $ являются базисными векторами плоскости — любой вектор $ vec $, лежащий в плоскости, через них выражается и они линейно независимы. Но $ X_ $ и $ X_ $ определяют фундаментальную систему решений однородного уравнения. Таким образом, мы получили геометрическую интерпретацию для ФСР: она задает базисные векторы плоскости, проходящей через начало координат.

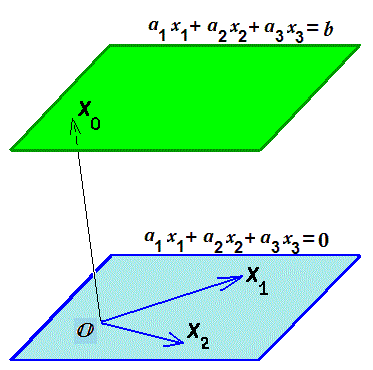
Теперь рассмотрим систему из двух уравнений: $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2. endright. $$ Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^ $. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа $$ operatorname left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) quad u quad operatorname left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) . $$ Очевидно, ни одно из них не может быть большим $ 2_ $. Если оба равны $ 2_ $ и этот факт обеспечен, например, условием $$ left| begin a_ & a_ \ a_ & a_ end right| ne 0, $$ то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_ $ и $ x_ $ и представить общее решение в виде: $$ x_1= frac<left|begin b_1 & a_ \ b_2 & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>+ frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 , quad x_2= frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>- frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 . $$ В этих формулах переменная $ x_ $ принимает любое значение, а значения переменных $ x_ $ и $ x_ $ линейно выражаются через $ x_ $. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами $$ left( begin x_1 \ x_2 \ x_3 end right)=X_0+tX_1 , $$ где вектор $$ quad X_0 = left(frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|> , frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 0right)^ $$ задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей), а вектор $$ X_1= left(frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, — frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 1 right)^ $$ является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_ $: $$ tilde X_1 = left(left|begin a_ & a_ \ a_ & a_ end right|, — left|begin a_ & a_ \ a_ & a_ end right|, left|begin a_ & a_ \ a_ & a_ end right| right)^ . $$ 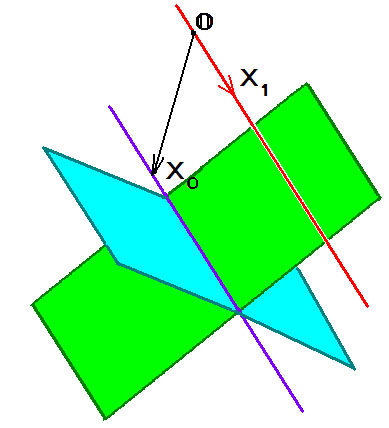Очевидно, что любой из векторов $ X_ $ или $ tilde X_1 $ задает фундаментальную систему решений однородной системы уравнений 10) $$ left<begin a_x_1 +a_x_2+a_x_3 &=&0,\ a_x_1 +a_x_2+a_x_3 &=&0. endright. $$ Последняя определяет прямую в $ mathbb R^3 $, проходящую через начало координат. Мы снова получаем интерпретацию теоремы: общее решение неоднородной системы получается сдвигом (параллельным переносом) общего решения однородной системы на вектор $ vec $.

Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^ $ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) $$ оказался меньшим $ 2_ $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль: $$ left| begin a_ & a_ \ a_ & a_ end right|=0, left| begin a_ & a_ \ a_ & a_ end right| =0, left| begin a_ & a_ \ a_ & a_ end right|=0 . $$ Эти условия можно переписать в виде $$ frac<a_><a_>=frac<a_><a_>=frac<a_><a_> ; $$ и, если обозначить общую величину последний отношений через $ tau_ $, то получаем: $$ (a_,a_,a_)=tau (a_,a_,a_) . $$ Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec<OA^> $ в $ mathbb R^ $, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы расширенная матрица системы $$ left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) $$ имела ранг меньший $ 2_ $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению $$ b_1 = tau b_2 $$ при величине $ tau_ $ определенной выше. При выполнении этого условия второе уравнение получается из первого домножением на $ tau_ $ и соответствующие плоскости попросту совпадают.

Перейдем теперь к системе из трех уравнений: $$ left< begin a_x_1 +&a_x_2+&a_x_3=&b_1, \ a_x_1 +&a_x_2+&a_x_3=&b_2, \ a_x_1 +&a_x_2+&a_x_3=&b_3. end right. $$ Вариантов взаимного расположения трех плоскостей в $ mathbb R^ $ уже значительно больше. Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден: если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью, как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное решение. Условие для этого случая «как правило» дается той же теоремой Крамера: $$ left| begin a_ & a_ & a_\ a_ & a_ & a_ \ a_ & a_ & a_ end right| ne 0 . $$

Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_ $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_,a_, a_) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2 endright. $$ определяет прямую в $ mathbb R^ $, то оба вектора $ vec<OA^> $ и $ vec<OA^> $ при $ A^= (a_,a_, a_) $ и $ A^= (a_,a_, a_) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость $$ a_x_1 +a_x_2+a_x_3 =b_3 $$ будет ей параллельна.

Статья не закончена!

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Ортогональность

Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.

Задача решения системы линейных уравнений $$ left< begin 3x_1&+4x_2&-x_3&=2, \ x_1&-2x_2&+3x_3&=1 end right. $$ может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде $$ x_1left(begin 3 \ 1 end right)+ x_2left(begin 4 \ -2 end right)+ x_3left(begin -1 \ 3 end right)= left(begin 2 \ 1 end right) , $$ можно говорить о поиске линейной комбинации столбцов $$ left(begin 3 \ 1 end right), left(begin 4 \ -2 end right), left(begin -1 \ 3 end right) $$ равной заданному столбцу $$ left(begin 2 \ 1 end right) . $$ В случае произвольной системы, записанной в матричном виде $$ A_X=mathcal B_ $$ совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_,dots,A_ $: $$ mathcal B=x_1 A_+dots+x_nA_ quad iff quad mathcal B in mathcal L (A_,dots,A_) . $$ В случае положительного ответа числа $ x_,dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов 11) $ <A_,dots,A_> $.

С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3,x_1+4,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ vec<^> $ и $ vec<> $ равно фиксированному числу $ 2_ $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_^ $; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle mbox rangle $, то систему уравнений можно переписать в виде $$ langle vec<^> , vec<> rangle=2, langle vec<^> , vec<> rangle=1 quad npu quad A^ = [3,4,-1], A^=[1,-2,3] $$ — строках матрицы $ A_ $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.

Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ left< begin 3x_1&+4x_2&-x_3&=0, \ x_1&-2x_2&+3x_3&=0 end right. $$ означает подобрать вектор $ vec<> $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec<^> $ и $ vec<^> $. Очевидно, что таких векторов в $ mathbb R^ $ бесконечно много — найдя хотя бы один такой вектор $ vec<> $, другие получим его растяжением: $ alpha cdot vec<> $ остается перпендикулярным векторам $ vec<^> $ и $ vec<^> $ при $ forall alpha in mathbb R $.

Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_^ $ строк или столбцов, состоящих из $ n_ $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см. ☞ ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой $$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$ и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^ $ и $ mathbb R^ $ свойства скалярного произведения будут выполнены.

В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_ $: $$ langle A^,X rangle=0, langle A^,X rangle=0,dots, langle A^,X rangle=0 . $$ Множество таких строк образует линейное подпространство пространства $ mathbb R_^ $, это подпространство является ортогональным дополнением линейной оболочки $ mathcal L ( A^, A^,dots, A^ ) $ в пространстве $ mathbb R_^ $. Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_ $ и обозначается 12) $ er (A) $. Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname $. Во введенных обозначениях теорема из ☞ ПУНКТА переформулируется так:

Теорема. $ operatorname left( er (A) right)=n- mathfrak r $, где $ n_ $ — количество столбцов матрицы $ A_ $, а $ mathfrak r=operatorname (A) $ — ее ранг.

💡 Видео

Видеоурок "Неопределенные системы"Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать

Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Решение системы уравнений методом ГауссаСкачать

Решение системы уравнений методом Крамера.Скачать

Неоднородная система линейных уравненийСкачать