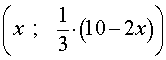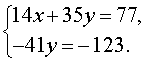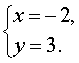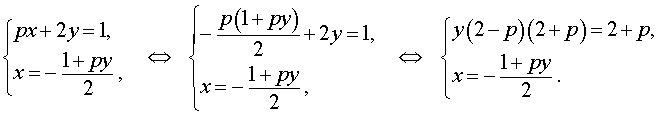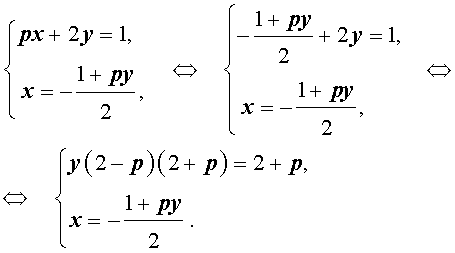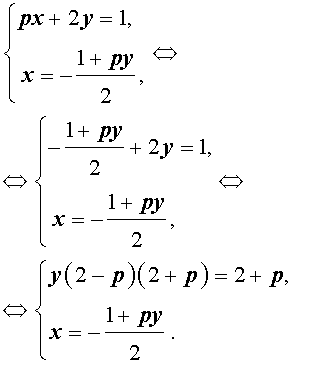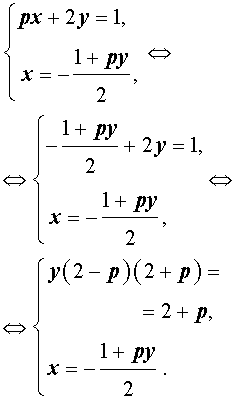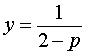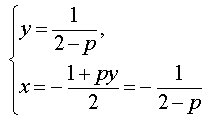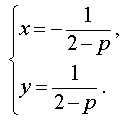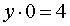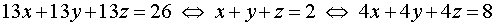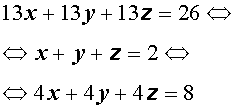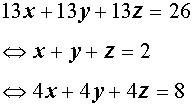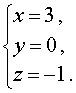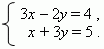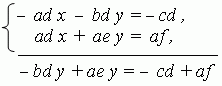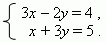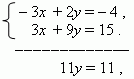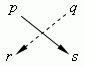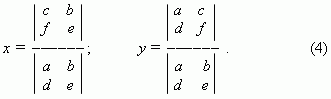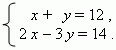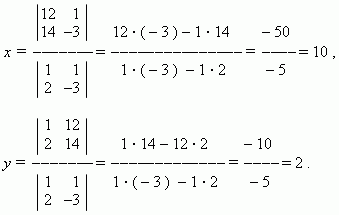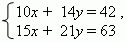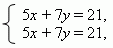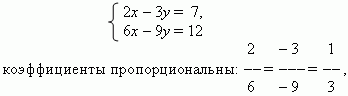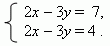Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Видео:7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
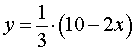 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
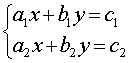 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
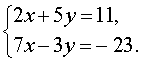 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
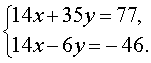 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
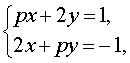 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
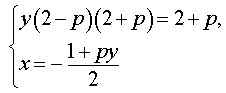 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
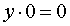
и его решением является любое число 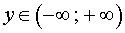
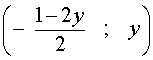
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:Алгебра 7 класс (Урок№48 - Решение систем двух линейных уравнений с двумя неизвестными.)Скачать

Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
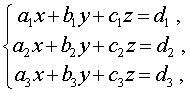 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
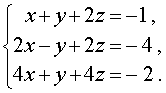 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
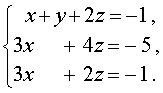 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
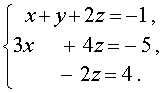 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
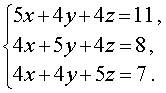 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра. 7 класс
Конспект урока
Решение систем двух линейных уравнений с двумя неизвестными
Перечень вопросов, рассматриваемых в теме:
- Систематизация решений систем уравнений.
- Использование отношений коэффициентов при решении систем уравнений.
- Практическое применение теоремы.
Пусть дана система уравнений:
где все коэффициенты отличны от нуля.
а) имеет единственное решение, если ;
б) не имеет решений, если ;
в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Решение систем двух линейных уравнений с двумя неизвестными.
Пусть дана система двух линейных уравнений с двумя неизвестными.
Перенеся все члены правых частей этих уравнений в левые части, и приведя подобные члены, получим равносильную данной систему вида:
где ─ некоторые числа.
Мы уже знаем, как решать такую систему, когда все коэффициенты при неизвестных отличны от нуля. Мы знаем так же, что если коэффициенты при неизвестных непропорциональны, то решение системы существует и единственно; если же коэффициенты при неизвестных системы пропорциональны, то либо решений бесконечно много, либо нет ни одного решения.
Нам остаётся рассмотреть те случаи, когда некоторые коэффициенты при неизвестных равны нулю. Рассмотрим это на характерных примерах.
Пример 1. Решим систему уравнений:
Второе уравнение этой системы имеет отличные от нуля коэффициенты при неизвестных, а первое уравнение имеет коэффициент при , отличный от нуля, и коэффициент при , равный нулю.
Эту систему проще решить методом подстановки. Найдем из первого уравнения:
И подставим его во второе. Получим:
Таким образом, пара чисел есть единственное решение системы.
Пример 2. Решим систему уравнений:
Система есть частный случай системы , где
Единственным решением этой системы является пара чисел
Пример 3. Решим систему уравнений:
Из каждого уравнения системы получим
Так как систему мы рассматриваем как частный случай системы , где то система может быть записана так:
Здесь может быть любым числом, а .
Таким образом, решения системы записываются в виде пар чисел , где ─ любое число.
Пример 4. Решим систему уравнений
Эта система противоречива (не имеет решений), потому что не может одновременно равняться и 1, и .
Пример 5. Решим систему уравнений:
Если , то эта система противоречива, потому что никакая пара чисел не удовлетворяет второму уравнению системы
Если , то второе уравнение обращается в верное равенство при любых Остаётся только первое уравнение. Оно уже рассматривалось. Следовательно, все решения первого уравнения являются решениями системы.
О количестве решений системы двух уравнений первой степени с двумя неизвестными.
Пусть дана система уравнений:
где все коэффициенты отличны от нуля.
а) имеет единственное решение, если ;
б) не имеет решений, если ;
в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.
Из первого уравнения системы получим, что:
. Подставив полученное выражение вместо во второе уравнение системы и учитывая, что получим уравнение:
Здесь возможны три случая.
- Если:
то уравнение имеет единственный корень, поэтому и система имеет единственное решение.
Так как и то условие можно записать в виде
- Если:
то уравнение не имеет корней и система не имеет решений.
Так как то условия можно записать в виде
- Если:
то уравнение имеет бесконечно много корней, поэтому и система имеет бесконечно много решений.
Так как то условия можно записать в виде
если то система имеет единственное решение;
если то система не имеет решений;
если то система имеет бесконечно много решений, и эти решения задаются парами , где любое число.
Пример 1. Определим число решений системы уравнений:
а) Так как выполняется условие , то система имеет единственное решение.
б) Так как выполняется условие , то система имеет бесконечно много решений.
в) Так как выполняется условие то система не имеет решений.
Ответ: а) единственное решение; б) бесконечно много решений; в) нет решений.
Пример 2. При каком значении система
не имеет решений?
Система не имеет решений, если выполняется условие
. Условие выполняется лишь при При этом условие также выполняется. Следовательно, система не имеет решений при
Пример 3. Существует ли значение , при котором система не имеет решений?
Система не имеет решений, если выполняется условие . Условие выполняется лишь при При этом условие не выполняется. Следовательно, таких не существует.
Ответ: не существует.
Разбор решения заданий тренировочного модуля.
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Впишите пропущенные элементы при решении системы.
Перенесем из первого уравнения в правую часть 4, получим
Найдем отношение коэффициентов при х и у в системе:
‑ так как отношения __ равны, значит, система имеет одно решение. Решим систему способом подстановки:
Перенесем из первого уравнения в левую часть 4, получим:
Найдем отношение коэффициентов при х и у в системе:
‑ так как отношения не равны, значит, система имеет одно решение. Решим систему способом подстановки:
№2. Тип задания: восстановление последовательности элементов горизонтальное / вертикальное.
Решите систему двух уравнений:
Значит, система имеет единственное решение.
Так как отношение коэффициентов равно —
Значит, система имеет единственное решение.
Так как отношение коэффициентов равно —
Значит, система имеет единственное решение.
Перенесем в первом уравнении из левой части в правую 4:
Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Системы двух линейных уравнений с двумя неизвестными
Системы двух линейных уравнений с двумя неизвестными.
Основные методы решения: подстановка, сложение или вычитание.
Определители второго порядка. Правило Крамера.
Исследование решений системы уравнений.
Системы двух линейных уравнений с двумя неизвестными имеют вид:
где a , b , c , d , e , f – заданные числа; x , y – неизвестные. Числа a , b , d , e – коэффициенты при неизвестных; c , f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.
1) Из одного уравнения выражаем одно из неизвестных, например x , через коэффициенты и другое неизвест ное y :
x = ( c – by ) / a . (2)
2) Подставляем во второе уравнение вместо x :
d ( c – by ) / a + ey = f .
3) Решая последнее уравнение, находим y :
y = ( af – cd ) / ( ae – bd ).
4) Подставляем это значение вместо y в выражение (2) :
x = ( ce – bf ) / ( ae – bd ) .
П р и м е р . Решить систему уравнений:
Из первого уравнения выразим х через коэффициенты и y :
Подставляем это выражение во второе уравнение и находим y :
( 2 y + 4 ) / 3 + 3 y = 5 , откуда y = 1 .
Теперь находим х, подставляя найденное значение вместо y в
выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .
Сложение или вычитание. Этот метод состоит в следующем.
1) Умножаем обе части 1- го уравнения системы (1) на (– d ), а обе части 2- го уравнения на а и складываем их:
Отсюда получаем: y = ( af – cd ) / ( ae – bd ) .
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b( af – cd ) / ( ae – bd ) = c .
3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ) .
П р и м е р . Решить систему уравнений:
методом сложения или вычитания.
Умножаем первое уравнение на –1, второе – на 3 и складываем их:
отсюда y = 1. Подставляем это значение во второе уравнение
(а в первое можно?): 3 x + 9 = 15, отсюда x = 2.
Определители второго порядка. Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:
Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:

Это выражение получается перекрёстным умножением чисел p , q , r , s :
и последующим вычитанием одного произведения из другого: ps – qr . Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак « – » — для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,
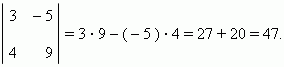
Выражение 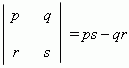
Правило Крамера. Используя определители, можно переписать формулы (3):
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.
П р и м е р . Решить систему уравнений
используя правило Крамера.
Р е ш е н и е . Здесь a = 1, b = 1, c = 12, d = 2, e = –3, f = 14 .
Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентов уравнений возможны три различных случая:
1) коэффициенты при неизвестных не пропорциональны: a : d ≠ b : e ,
в этом случае система линейных уравнений имеет единственное решение, получаемое по формулам (4);
2) все коэффициенты уравнений пропорциональны: a : d = b : e = c : f ,
в этом случае система линейных уравнений имеет бесконечное множество реше ний , так как здесь мы имеем фактически одно уравнение вместо двух.
П р и м е р . В системе уравнений
и эта система уравнений имеет бесконечное множество решений.
Разделив первое уравнение на 2, а второе – на 3, мы получим два
т.е. фактически одно уравнение с двумя неизвестными, у которого
бесконечное множество решений.
3) коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам : a : d = b : e ≠ c : f ,
в этом случае система линейных уравнений не имеет решений, так как мы имеем противоречивые уравнения.
П р и м е р . В системе уравнений
но отношение свободных членов 7 / 12 не равно 1 / 3.
Почему эта система не имеет решений? Ответ очень простой.
Разделив второе уравнение на 3, мы получим:
Уравнения этой системы противоречивы, потому что одно и то
же выражение 2 x – 3 y не может быть одновременно равно и 7, и 4.
Copyright © 2004 — 2007 Др. Юрий Беренгард. All rights reserved.
💥 Видео
Линейное уравнение с двумя переменными. 7 класс.Скачать

Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Системы двух линейных уравнений с двумя переменными. 6 класс.Скачать

7 класс, 40 урок, Системы двух линейных уравнений с двумя переменными как математические моделиСкачать

Система двух линейных уравнений с двумя переменными и ее решениеСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Решение систем уравнений методом подстановкиСкачать

Системы двух уравнений первой степени с двумя неизвестнымиСкачать

Решение систем двух линейных уравнений с двумя неизвестнымиСкачать

Система уравнений. Метод алгебраического сложенияСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать