Продолжаем изучать методы решения уравнений. Сейчас мы в деталях разберем метод возведения обеих частей уравнения в одну и ту же степень. Начнем с теории: рассмотрим, для решения каких уравнений применяется метод, опишем, в чем он состоит, приведем теоретическое обоснование метода возведения обеих частей уравнения в одну и ту же степень, запишем соответствующие алгоритмы решения уравнений. После этого сосредоточимся на практике и рассмотрим разнообразные примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень.
- Для решения каких уравнений применяется
- В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
- Обоснование метода
- Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
- Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
- Когда обе части уравнения можно возводить в степень
- можно ли возводить в степень обе части уравнения ? ( слева и справа от знака равно )
- Лучший ответ
- Ответы
- Похожие вопросы
- 📽️ Видео
Видео:✓ Как возводить в иррациональную степень | Ботай со мной #017 | Борис ТрушинСкачать

Для решения каких уравнений применяется
Метод возведения обеих частей уравнения в одну и ту же степень в первую очередь применяется для решения иррациональных уравнений. Это объясняется тем, что возведение в натуральную и большую единицы степень позволяет избавляться от корней. Например, возведение в степень позволяет избавляться от корней при решении следующих уравнений:
, C≥0 , в частности,
,
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
и дальше — к элементарному уравнению 4−5·x=0 .
, например,
,
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и
, таких как
,
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
- уравнений с двумя, тремя корнями в записи, например,
и
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
- уравнений, в которых под знаком корня находятся другие корни, к примеру,
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
- и это не весь список.
Метод возведения обеих частей уравнения в одну и ту же степень используется и для решения некоторых уравнений, в которых переменная находится в основаниях степеней с дробными показателями. Например, уравнение 
Также метод возведения частей уравнения в степень применяется при решении некоторых степенных уравнений, в которых фигурируют иррациональные показатели. В пример приведем два уравнения 



Видео:НЕРАВЕНСТВА возведение в степень 9 класс МакарычевСкачать

В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
Метод состоит в переходе к уравнению, которое получается из исходного путем возведения его обеих частей в одну и ту же степень, и нахождении решения исходного уравнения по решению полученного уравнения.
На практике наиболее часто прибегают к возведению обеих частей уравнения в одну и ту же натуральную степень, большую единицы, то есть, в квадрат, куб и т.д. Делается это на базе следующего утверждения:
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень, большую единицы, дает равносильное уравнение (см. равносильные уравнения и уравнения-следствия).
Реже приходится обращаться к возведению обеих частей уравнения в другие степени, в частности, в дробные рациональные и иррациональные. В этих случаях отталкиваются от такого утверждения:
Уравнение A(x)=B(x) , на области допустимых значений переменной x для которого A(x)>0 или A(x)≥0 , B(x)>0 или B(x)≥0 , равносильно уравнению A r (x)=B r (x) , где r – положительное действительное число.
Видео:Возведение в степень произведения и степени. Алгебра, 7 классСкачать

Обоснование метода
Обоснованием метода возведения обеих частей уравнения в одну и ту же степень является доказательство утверждений из предыдущего пункта. Приведем эти доказательства.
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Докажем его для уравнений с одной переменной. Для уравнений с несколькими переменными принципы доказательства те же.
Пусть A(x)=B(x) – исходное уравнение и x0 – его корень. Так как x0 является корнем этого уравнения, то A(x0)=B(x0) – верное числовое равенство. Мы знаем такое свойство числовых равенств: почленное умножение верных числовых равенств дает верное числовое равенство. Умножим почленно 2·k , где k – натуральное число, верных числовых равенств A(x0)=B(x0) , это нам даст верное числовое равенство A 2·k (x0)=B 2·k (x0) . А полученное равенство означает, что x0 является корнем уравнения A 2·k (x)=B 2·k (x) , которое получено из исходного уравнения путем возведения его обеих частей в одну и ту же четную натуральную степень 2·k .
Для обоснования возможности существования корня уравнения A 2·k (x)=B 2·k (x) , который не является корнем исходного уравнения A(x)=B(x) , достаточно привести пример. Рассмотрим иррациональное уравнение 





Так доказано, что возведение обеих частей уравнения в одну и ту же четную натуральную степень приводит к уравнению-следствию.
Остается доказать, что возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Покажем, что каждый корень уравнения является корнем уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, и обратно, что каждый корень уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, является корнем исходного уравнения.
Пусть перед нами уравнение A(x)=B(x) . Пусть x0 – его корень. Тогда является верным числовое равенство A(x0)=B(x0) . Изучая свойства верных числовых равенств, мы узнали, что верные числовые равенства можно почленно умножать. Почленно умножив 2·k+1 , где k – натуральное число, верных числовых равенств A(x0)=B(x0) получим верное числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) , которое означает, что x0 является корнем уравнения A 2·k+1 (x)=B 2·k+1 (x) . Теперь обратно. Пусть x0 – корень уравнения A 2·k+1 (x)=B 2·k+1 (x) . Значит числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) — верное. В силу существования корня нечетной степени из любого действительного числа и его единственности будет верным и равенство 

Так доказано, что возведение обеих частей иррационального уравнения в нечетную степень дает равносильное уравнение.
Доказанное утверждение пополняет известный нам арсенал, использующийся для решения уравнений, еще одним преобразованием уравнений – возведением обеих частей уравнения в одну и ту же натуральную степень. Возведение в одну и ту же четную степень обеих частей уравнения является преобразованием, приводящим к уравнению-следствию, а возведение в нечетную степень – равносильным преобразованием. На этом преобразовании базируется метод возведения обеих частей уравнения в одну и ту же степень.
Утверждение, касающееся возведения обеих частей уравнения в одну и ту же положительную действительную степень, доказывается аналогично с опорой на единственность степени положительного числа с действительным показателем.
Видео:Решение иррациональных уравнений методом возведения обеих частей в степень. ГВЭ11 + ЕГЭ 2021 #56Скачать

Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
Есть смысл записать три алгоритма решения уравнений методом возведения обеих частей уравнения в одну и ту же степень: первый – для возведения в нечетную степень, второй – для возведения в четную степень, третий – для возведения в ненатуральную положительную степень.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же нечетную степень:
- Обе части уравнения возводятся в одну и ту же нечетную степень 2·k+1 .
- Решается полученное уравнение. Его решение есть решение исходного уравнения.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же четную степень:
- Обе части уравнения возводятся в одну и ту же четную степень 2·k .
- Решается полученное уравнение.
- Если полученное уравнение не имеет корней, то делается вывод об отсутствии корней у исходного уравнения.
- Если полученное уравнение имеет корни, то проводится отсеивание посторонних корней любым методом, не завязанным на области допустимых значений, например, через проверку подстановкой.
Обратите внимание: этот алгоритм, в отличие от предыдущего, содержит пункт, касающийся отсеивания посторонних корней. Это связано с тем, что возведение обеих частей уравнения в одну и ту же нечетную степень приводит к равносильному уравнению, а возведение обеих частей уравнения в четную степень в общем случае приводит к уравнению-следствию. Поэтому, в результате возведения в нечетную степень посторонние корни не возникают, а при возведении в четную степень посторонние корни могут появиться. Таким образом, при возведении частей уравнения в четную степень возникает необходимость в отсеивании посторонних корней. Почему отсеивание посторонних корней в этом случае нужно проводить методом, не использующим ОДЗ? Потому что возведение обеих частей уравнения в четную степень может приводить к появлению посторонних корней в пределах ОДЗ, и отсеять их по ОДЗ или по условиям ОДЗ невозможно.
Наконец, запишем алгоритм решения уравнений методом возведения обеих частей в одну и ту же положительную дробную рациональную или иррациональную степень:
- Убеждаемся, что выражения в левой и правой части уравнения не принимают отрицательных значений на ОДЗ для решаемого уравнения.
- Возводим обе части уравнения в одну и ту же положительную степень.
- Решаем полученное уравнение. Его решение дает искомое решение исходного уравнения.
Видео:Иррациональное уравнение 634. Метод возведения обоих частей уравнения в одну и ту же степень.Скачать

Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
Большое количество попадающих под разбираемую тему примеров с подробными решениями приведено в статье решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. В добавление к этим примерам стоит разобрать решение уравнения через возведение обеих частей уравнения в одну и ту же степень, не являющуюся натуральным числом.
Решите уравнение
Решать заданное уравнение можно несколькими разными методами. Например, можно провести решение методом логарифмирования. Также можно преобразовать уравнение к виду 

Учитывая свойство степени в степени (см. свойства степеней), несложно догадаться, что избавиться от иррациональных показателей позволяет возведение обеих частей уравнения в степень 

Итак, проводим возведение обеих частей уравнения 


Решаем полученное уравнение:
Так мы пришли к кубическому уравнению x 3 −x 2 +2=0 . Один его корень x=−1 легко подбирается. Разделив многочлен x 3 −x 2 +2 на двучлен x+1 , получаем возможность представить кубическое уравнение в виде (x+1)·(x 2 −2·x+2)=0 . Квадратное уравнение x 2 −2·x+2=0 не имеет решений, так как его дискриминант отрицательный. Из этого заключаем, что уравнение x 3 −x 2 +2=0 имеет единственный корень x=−1 .
В процессе решения мы дважды отмечали, что нам будет необходимо сделать проверку найденных корней. Сейчас пришло это время. Проверку выполним через подстановку найденного корня x=−1 в исходное уравнение 
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Когда обе части уравнения можно возводить в степень
Ключевые слова: решение уравнения, тождественное преобразование, тождественные преобразования, посторонний корень, потеря корня.
Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим уравнением, ему равносильным . Такая замена называется тождественным преобразованием .
Основные тождественные преобразования:
Замена одного выражения другим, тождественно равным ему. Например, уравнение ( 3x+ 2 ) 2 = 15x+10 можно заменить следующим равносильным: 9x 2 + 12x + 4 = 15x + 10
Перенос членов уравнения из одной стороны в другую с обратными знаками. Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком « – »: 9x 2 + 12x + 4 – 15x – 10 = 0, после чего полу чим: 9x 2 – 3x – 6 = 0 .
Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Это очень важно, так как новое уравнение может не быть равносильным предыдущему, если выражение, на которое мы умножаем или делим, может быть равно нулю. Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение ( x – 1 )( x – 3 ) = 0, у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление может привести к потере корня. Так, если ( x – 1 )( x – 3 ) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x – 3 .
Можно возвести обе части уравнения в нечетную степень или извлечь и з обеих частей уравнения корень нечетной степени . Необходимо помнить, что: а) возведение в четную степень может привести к приобретению посторонних корней ; б) неправильное извлечение корня четной степени может привести к потере корней.
Уравнение 7 x = 35 имеет единственный корень x = 5 . Возведя обе части этого уравнения в квадрат, получим уравнение: 49 x 2 = 1225 ,
имеющее два корня: x = 5 и x = – 5. Последнее значение является посторонним корнем. Неправильное извлечение квадратного корня из обеих
частей уравнения 49 x 2 = 1225 даёт в результате 7 x = 35,и мы теряем корень x = – 5. Правильное извлечение квадратного корня приводит к
уравнению: | 7 x | = 35, а следовательно, к двум случаям: 1) 7 x = 35, тогда x = 5 ; 2) – 7 x = 35, тогда x = – 5 .Следовательно, при правильном извлечении квадратного корня мы не теряем корней уравнения.
Пример. Решите уравнение $$sqrt<x^-x> + sqrt<2 — x — x^> = sqrt — 1$$
Решение. В этом примере наоборот сложно его решение. Однако поиск ОДЗ приносит несомненную пользу.
В самом деле, ОДЗ: $$left< begin
x^2 — x ge 0 \
2 — x — x^2 ge 0 \
x ge 0
end right., Leftrightarrow left< begin
x in left( right] cup left[ right) \
x in left[ right] \
x in left[ right)
end right., Leftrightarrow left[ begin
x = 0 \
x = 1
end right.$$
Значит, ОДЗ нашего уравнения содержит только два числа. А поскольку вне ОДЗ решений быть не может, то корнями нашего уравнения могут быть только эти два числа. Для того чтобы понять, какое из них действительно является решением, нужно полученные числа подставить в уравнение. Подстановка даёт, что x = 0 не является решением уравнения, а x = 1 − является.
Ответ. 1.
Таким образом, к понятию ОДЗ нужно относиться творчески и искать его, только если в этом возникает существенная необходимость. Так, например, в равносильном переходе $$sqrt = g(x), Leftrightarrow left< begin
g(x) ge 0, \
f(x) = g^2 (x)
end right.$$
требование g ( x ) ? 0 задает ОДЗ. Однако, если искать g ( x ) очень сложно, то проще подставить найденные корни в исходное уравнение, чем выяснять, при каких x выполнено неравенство g ( x ) ? 0.
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

можно ли возводить в степень обе части уравнения ? ( слева и справа от знака равно )
Вопрос решен и закрыт.
Видео:Математика - Возведение в степеньСкачать

Лучший ответ
ovod (73) 7 (86376) 8 18 75 11 лет
Можно (а иногда это единственный способ решить уравнение), но это может привести к появлению лишних корней, если возводить в четную степень.
Поэтому необходимо либо определить область допустимых значений неизвестных в исходном уравнении и потом сравнить с ней найденные решения, либо сделать проверку всех найденных решений в исходном уравнении.
Видео:Система иррациональных уравнений #3Скачать

Ответы
Mirona (29) 5 (3166) 13 27 11 лет
FunTime 6 (13045) 3 27 55 11 лет
лол. да.
обе стороны в одинаковую степень.
часто что бы избавиться от квадратного корня возводятся в степень обе стороны уравнения.
Arix 6 (16373) 3 11 25 11 лет
можно. если обе части и в одинаковую) в квадрат,к примеру, чтобы избавиться от корня
TvojaPsihi4ka (29) 6 (7304) 6 36 69 11 лет
можно ,а иногда даже нужно возводить всё уравнение в степень! хД т.е. и то что до и то что после знака равно хД главное что бы тебе это надо было,а не просто так хД
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Похожие вопросы
а так хотелось, солнце моё, ответить в рифму!
Каждый день приношу продукты и помогаю в уборке. она не ветеран, но она прошла войну, прошла подростком, потом в эвакуации, потом в плен почти попали, пережила раскулачивание и много чего ещё. сейчас одна, все родственники либо её возраста либо за границей либо уже давно на том свете.
согласна, многие именно тогда и вспоминают. жаль. с каждым годом всё меньше и меньше.. я в прошлом году (когда поздравлять ходила) многим могла цветы подарить, пообщаться.. сегодня я еле еле нашла 10 ветеранов. аж страшно становится .
может инженерный калькулятор?
там кнопка есть x^y.
набираешь то что хочешь возвести в степень, жмёшь на кнопку, набираешь нужную степень, жмёшь равно.
📽️ Видео
показательно степенное уравнение методом логарифмирования обеих частей уравненияСкачать

Подготовка к ЕГЭ #56. Решение иррациональных уравнений методом возведения обеих частей в степеньСкачать

Показательно степенное уравнениеСкачать

Решение логарифмических уравнений ПРИМЕР #11 Раскладывать на множители или делитьСкачать

Как решают уравнения в России и СШАСкачать

Как решать уравнения с дробной степеньюСкачать

ОТРИЦАТЕЛЬНАЯ СТЕПЕНЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Более сложные иррациональные уравнения. Иррациональные уравнения Часть 2 из 2Скачать

Система иррациональных уравнений #2Скачать

Решение иррациональных уравнений.Скачать

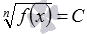 , C≥0 , в частности,
, C≥0 , в частности,  ,
,  и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению 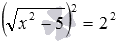 , и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению 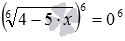 и дальше — к элементарному уравнению 4−5·x=0 .
и дальше — к элементарному уравнению 4−5·x=0 .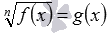 , например,
, например,  ,
,  и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.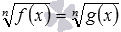 и
и  , таких как
, таких как 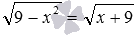 ,
, 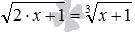 и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень. и
и  . В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала. . Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.



