Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _left ( x^+x right )=log _left ( x^-4 right )Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ alt=’2^<log _left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _left ( 4x+5 right )>>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ />
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
- Решение логарифмических уравнений. Как решать, на примерах.
- Решение простейших логарифмических уравнений
- Алгебра
- Уравнения вида logaf(x) = logag(x)
- Уравнения, требующие предварительных преобразований
- Логарифмические уравнения с заменой переменных
- Логарифмирование уравнений
- Переход от логарифмических неравенств к нелогарифмическим
- 💡 Видео
Видео:Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать

Решение логарифмических уравнений. Как решать, на примерах.
Логарифмическим уравнением называется уравнение, в котором неизвестное (х) и выражения с ним находятся под знаком логарифмической функции. Решение логарифмических уравнений подразумевает, что вы уже знакомы с понятием и видами логарифмов и основными формулами.
Как решать логарифмические уравнения?
Самое простое уравнение имеет вид logax = b, где a и b -некоторые числа,x — неизвестное.
Решением логарифмическое уравнения является x = a b при условии: a > 0, a 1.
Следует отметить, что если х будет находиться где-нибудь вне логарифма, например log2х = х-2, то такое уравнение уже называется смешанным и для его решения нужен особый подход.
Идеальным случаем является ситуация, когда Вам попадется уравнение, в котором под знаком логарифма находятся только числа, например х+2 = log22. Здесь достаточно знать свойства логарифмов для его решения. Но такая удача случается не часто, поэтому приготовьтесь к более сложным вещам.
Но сначала, все-таки, начнём с простых уравнений. Для их решения желательно иметь самое общее представление о логарифме.
Решение простейших логарифмических уравнений
К таковым относятся уравнения типа log2х = log216. Невооруженным глазом видно, что опустив знак логарифма получим х = 16.
Для того, чтобы решить более сложное логарифмическое уравнение, его обычно приводят к решению обычного алгебраического уравнения или к решению простейшего логарифмического уравнения logax = b. В простейших уравнениях это происходит в одно движение, поэтому они и носят название простейших.
Вышеиспользованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. В математике эта операция носит название потенцирования. Существуют определенные правила или ограничения для подобного рода операций:
- одинаковые числовые основания у логарифмов
- логарифмы в обоих частях уравнения находятся свободно, т.е. без каких бы то ни было коэффициентов и других разного рода выражений.
Скажем в уравнении log2х = 2log2 (1- х) потенцирование неприменимо — коэффициент 2 справа не позволяет. В следующем примере log2х+log2 (1 — х) = log2 (1+х) также не выполняется одно из ограничений — слева логарифма два. Вот был бы один – совсем другое дело!
Вообщем, убирать логарифмы можно только при условии, что уравнение имеет вид:
В скобках могут находится совершенно любые выражения, на операцию потенцирования это абсолютно никак не влияет. И уже после ликвидации логарифмов останется более простое уравнение – линейное, квадратное, показательное и т.п., которое Вы уже, надеюсь, умеете решать.
Возьмем другой пример:
Применяем потенцирование, получаем:
Пойдем дальше. Решим следующий пример:
Исходя из определения логарифма, а именно, что логарифм — это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (4х-1), получаем:
Дальше уже дело техники:
Опять получили красивый ответ. Здесь мы обошлись без ликвидации логарифмов, но потенцирование применимо и здесь, потому как логарифм можно сделать из любого числа, причем именно такой, который нам надо. Этот способ очень помогает при решении логарифмических уравнений и особенно неравенств.
Решим наше логарифмическое уравнение log3 (2х-1) = 2 с помощью потенцирования:
Представим число 2 в виде логарифма, например, такого log39, ведь 3 2 =9.
Тогда log3 (2х-1) = log39 и опять получаем все то же уравнение 2х-1 = 9. Надеюсь, все понятно.
Вот мы и рассмотрели как решать простейшие логарифмические уравнения, которые на самом деле очень важны, ведь решение логарифмических уравнений, даже самых страшных и закрученных, в итоге всегда сводится к решению простейших уравнений.
Во всем, что мы делали выше, мы упускали из виду один очень важный момент, который в последующем будет иметь решающую роль. Дело в том, что решение любого логарифмического уравнения, даже самого элементарного, состоит из двух равноценных частей. Первая – это само решение уравнения, вторая — работа с областью допустимых значений (ОДЗ). Вот как раз первую часть мы и освоили. В вышеприведенных примерах ОДЗ на ответ никак не влияет, поэтому мы ее и не рассматривали.
А вот возьмем другой пример:
Внешне это уравнение ничем не отличается от элементарного, которое весьма успешно решается. Но это не совсем так. Нет, мы конечно же его решим, но скорее всего неправильно, потому что в нем кроется небольшая засада, в которую сходу попадаются и троечники, и отличники. Давайте рассмотрим его поближе.
Допустим необходимо найти корень уравнения или сумму корней, если их несколько:
Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.
Находим корни уравнения:
Получилось два корня.
С первого взгляда все правильно. Но давайте проверим результат и подставим его в исходное уравнение.
Проверка прошла успешно, теперь очередь х2= -1:
Так, стоп! Внешне всё идеально. Один момент — логарифмов от отрицательных чисел не бывает! А это значит, что корень х = -1 не подходит для решения нашего уравнения. И поэтому правильный ответ будет 3, а не 2, как мы написали.
Вот тут-то и сыграла свою роковую роль ОДЗ, о которой мы позабыли.
Напомню, что под областью допустимых значений принимаются такие значения х, которые разрешены или имеют смысл для исходного примера.
Без ОДЗ любое решение, даже абсолютно правильное, любого уравнения превращается в лотерею — 50/50.
Как же мы смогли попасться при решении, казалось бы, элементарного примера? А вот именно в момент потенцирования. Логарифмы пропали, а с ними и все ограничения.
Что же в таком случае делать? Отказываться от ликвидации логарифмов? И напрочь отказаться от решения этого уравнения?
Нет, мы просто, как настоящие герои из одной известной песни, пойдем в обход!
Перед тем, как приступать к решению любого логарифмического уравнения, будем записывать ОДЗ. А вот уж после этого можно делать с нашим уравнением все, что душа пожелает. Получив ответ, мы просто выбрасываем те корни, которые не входят в нашу ОДЗ, и записываем окончательный вариант.
Теперь определимся, как же записывать ОДЗ. Для этого внимательно осматриваем исходное уравнение и ищем в нем подозрительные места, вроде деления на х, корня четной степени и т.п. Пока мы не решили уравнение, мы не знаем – чему равно х, но твердо знаем, что такие х, которые при подстановке дадут деление на 0 или извлечение квадратного корня из отрицательного числа, заведомо в ответ не годятся. Поэтому такие х неприемлемы, остальные же и будут составлять ОДЗ.
Воспользуемся опять тем же уравнением:
Как видим, деления на 0 нет, квадратных корней также нет, но есть выражения с х в теле логарифма. Тут же вспоминаем, что выражение, находящееся внутри логарифма, всегда должно быть >0. Это условие и записываем в виде ОДЗ:
Т.е. мы еще ничего не решали, но уже записали обязательное условие на всё подлогарифменное выражение. Фигурная скобка означает, что эти условия должны выполняться одновременно.
ОДЗ записано, но необходимо еще и решить полученную систему неравенств, чем и займемся. Получаем ответ х > v3. Теперь точно известно – какие х нам не подойдут. А дальше уже приступаем к решению самого логарифмического уравнения, что мы и сделали выше.
Получив ответы х1= 3 и х2= -1, легко увидеть, что нам подходит лишь х1= 3, его и записываем, как окончательный ответ.
На будущее очень важно запомнить следующее: решение любого логарифмического уравнения делаем в 2 этапа. Первый — решаем само уравнение, второй – решаем условие ОДЗ. Оба этапа выполняются независимо друг от друга и только лишь при написании ответа сопоставляются, т.е. отбрасываем все лишнее и записываем правильный ответ.
Для закрепления материала настоятельно рекомендуем посмотреть видео:
На видео другие примеры решения лог. уравнений и отработка метода интервалов на практике.
На это по вопросу, как решать логарифмические уравнения, пока всё. Если что то по решению лог. уравнений осталось не ясным или непонятным, пишите свои вопросы в комментариях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Алгебра
План урока:
Задание. Укажите корень логарифмического уравнения
Задание. Решите урав-ние
В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид
Задание. Найдите решение логарифмического уравнения
Задание. Решите урав-ние
Задание. Решите урав-ние
Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Уравнения вида logaf(x) = logag(x)
Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.
Задание. Решите урав-ние
Задание. Найдите корень урав-ния
Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид
С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.
Задание. Решите урав-ние
Получили квадратное уравнение, которое решаем с помощью дискриминанта:
Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:
Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:
Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).
Видео:84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Уравнения, требующие предварительных преобразований
Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x).
Задание. Решите урав-ние
с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:
Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:
Задание. Решите урав-ние
Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем
Задание. Решите урав-ние
Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать:
Задание. Решите урав-ние
Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что
Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что
Задание. Решите урав-ние
Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу
Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:
Видео:Логарифмические уравнения 🥷🏿Скачать

Логарифмические уравнения с заменой переменных
Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.
Задание. Решите уравнение методом замены переменной
Задание. Найдите решение уравнения методом замены переменной
Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:
Видео:Логарифмические уравнения. 11 класс.Скачать

Логарифмирование уравнений
Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.
Задание. Укажите корни урав-ния
Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:
Возвращаемся от переменной t к переменной х:
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Переход от логарифмических неравенств к нелогарифмическим
Рассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства
Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.
Задание. Найдите решение логарифмического неравенства
Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas:
Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение
Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:
Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).
💡 Видео
Логарифмическое уравнение / Как решить?Скачать

ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ: ОДЗ ИЛИ НЕ ОДЗ?Скачать

Проще простого! Как решить Логарифмическое Уравнение?Скачать

Умножаем логарифмы В УМЕ🧠Скачать

Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

КАК СЧИТАТЬ ЛОГАРИФМЫ? #егэматематика2022 #егэ2022 #логарифмы #математика #егэ #огэ #shortsСкачать

Логарифмы-1. Уравнения: от базы до олимпиадСкачать

Интересная задача на логарифмы в ЕГЭСкачать

Десятичный логарифмСкачать
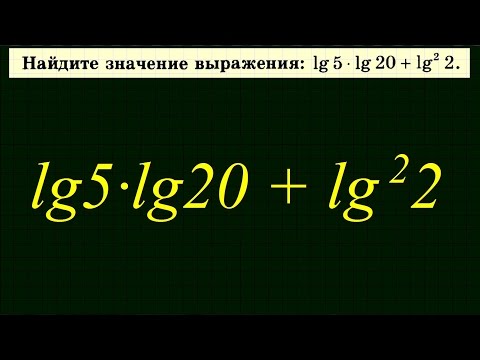
Логарифмы в ЕГЭ⚡️что получилось?!Скачать

10 класс. Алгебра. Логарифмические уравнения, сводящиеся к квадратным.Скачать

Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать
