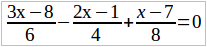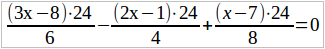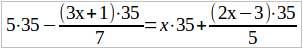Когда можно домножить обе части уравнения (3 видео)

Содержание

Когда можно домножить обе части уравнения
Когда можно домножить обе части уравнения
Математика
🎬 Видео

Видео:Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать

Когда можно домножить обе части уравнения

РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ

§ 4. Дополнительные замечания о решении уравнений.

Выше было сказано, что обе части уравнения можно умножать или делить на одно и то же количество. Говоря это, мы понимаем возможность этих действий в том смысле, что, производя их над данным уравнением, мы получаем новое уравнение, совместное с данным. Заметим теперь, что это указание верно только в том случае, когда множитель или делитель есть или явное количество, или хотя и неявное, но не содержит в себе той самой неизвестной буквы, которая входит в уравнение. Если дано выражение, содержащее то же неизвестное, как и в уравнении, то, вообще говоря, нельзя ни помножать уравнение на это выражение, ни делить на него. Поясним это на примерах:

Возьмем уравнение х = 2, которое очевидно имеет один только корень 2. Если мы умножим обе части его на х, то новое уравнение х 2 =2х не будет уже совместно с данным, потому что кроме прежнего корня 2, оно будет иметь еще корень 0, что обнаруживается и прямо из самаго уравнения, а также при решении полученного уравнения, если заменить его уравнением х 2 —2х=0 и написать последное в виде х(х—2)=0. Подобно этому, умножая данное уравнение х = 2 на выражение х—1, получаем новое уравнение
х 2 —2х=2х —2, совместное с уравнением (х—1)(х—2)=0 и имеющее два корня, прежний 2 и новый 1. Вообще при умножении уравнения на выражение, содержащее неизвестное, в это уравнение вводятся посторонние корни, а именно те, которые обращают множитель в нуль.

ІІонятно, наоборот, что если мы имеем, напр., уравнение х 2 =3х , корни которого суть 0 и 3 и сократим его на х, то полученное от этого сокращеиия уравнение не будет совместно с данным, потому что оно имеет только один корень 3. Подобно этому, имея уравнение (х—2) 2 =2х—4, корни которого суть 2 и 4, и сократив обе части на х—2, мы теряем корень 2 и получаем уравнение х—2 = 2, имеющее только один корень 4. Вообще при со-кращении обеих частей уравнения на их общий множитель, содержащий неизвестное, теряются корни уравнения и именно те, которые обращают делитель в нуль.

В курсе алгебры доказывается, что уравнение можно умножать на множитель, содержащий неизвестное, только в том случае, когда этот множитель входит в знаменатель дроби, получившейся от соединения всех дробей, входящих в уравнение, в одну дробь, и после окончательного сокращения этой последней.Так, если уравнение имеет вид А+ В /_С=0, где А есть совокупность всех целых членов, а В /_С есть несократимая дробь, то, умножая на С, получим уравнение АС+В=0, совместное с данным. В противном случае, если дробь В /_С сократима, то необходимо сократить ее раньше уничтожения ее знаменателя, чтобы не внести в уравнение постороннего ему корня.

Обратно, только тогда можно разделить обе части уравнения на выражение, содержащее неизвестное, когда от этого получатся такие дроби, которые, будучи соединены все в одной части уравнения, дают в результате дробь, не сокращающуюся ни на какой множитель, содержащий неизвестное. В противном случае нужно при сокращении уравнения на делитель, заметить тот корень, который теряется при этом сокращении, и считать его в числе корней данного уравнения.

В нижеследующих задачах звездочкой обозначены те уравнения, при решении которых нужно принимать во внимаиие сделанные выше указания. Остальные задачи можно решать по обыкновенным правилам.

Видео:Теория. Умножение и деление обеих частей уравнения (5-8 класс)Скачать

Когда можно домножить обе части уравнения

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
Нуль-одночлен степени не имеет.

Многочлены

Выражение, являющееся суммой нескольких одночленов, называют многочленом.
Одночлены, из которых состоит многочлен, называют членами многочлена.
Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
Графиком линейной функции является прямая.
Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

все решения уравнения являются координатами точек, принадлежащих графику;
координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

построить в одной координатной плоскости графики уравнений, входящих в систему;
найти координаты всех точек пересечения построенных графиков;
полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

если прямые пересекаются, то система имеет единственное решение.
если прямые совпадают, то система имеет бесконечно много решении.
если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

выразить из любого уравнения системы одну переменную через другую;
подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
решить уравнение с одной переменной, полученное на втором шаге;
подставить найденное значение переменной в выражение, полученное на первом шаге;
вычислить значение второй переменной;
записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
сложить почленно левые и правые части уравнений, полученных на первом шаге
решить уравнение с одной переменной, полученной на втором шаге
подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
вычислить значение второй переменной;
записать ответ.

Видео:Как умножать или делить обе части уравнения на одно и тоже число.Скачать

Математика

50. Свойства равенств, на которых основывается решение уравнений . Возьмем какое-нибудь уравнение, не очень сложное, например:

x/2 – (x – 3)/3 – (x – 5)/6 = 1

Мы видим в каждом уравнении знак равенства: все то, что написано слева от знака равенства, называется левою или первою частью уравнения (в первом уравнении 7x – 24 является левою или первою частью, а во втором x/2 – (x – 3)/3 – (x – 5)/6 есть первая, или левая, часть); все то, что написано справа от знака равенства, называется правою или второю частью уравнения (15 – 3x есть правая часть первого уравнения, 1 является правою, или вторю, частью 2-го уравнения).

Каждая часть любого уравнения выражает собою некоторое число. Числа, выражаемые левою и правою частью уравнения, должны быть равны между собою. Нам ясно: если мы к каждому из этих чисел прибавим по одинаковому числу, либо вычтем из них по одинаковому числу, либо каждое из них умножим на одинаковое число, либо, наконец, разделим на одно и то же число, то результаты этих действий должны также быть равными между собою. Другими словами: если a = b, то a + c = b + c, a – c = b – c, ac = bc и a/c = b/c. По поводу деления следует, однако, иметь в виду, что в арифметике не имеется деления на нуль — мы не умеем, например, число 5 разделить на нуль. Поэтому в равенстве a/c = b/c число c не может быть равным нулю.

К обеим частям уравнения можно прибавить или из них вычесть по одинаковому числу.
Обе части уравнения можно умножить или разделить на одно и то же число, исключая случай, когда это число может оказаться равным нулю.

Пользуясь этими свойствами уравнения, мы можем найти удобный способ решать уравнения. Выясним этот случай на примерах.

Пример 1. Пусть надо решить уравнение

Мы видим, что первая часть уравнения содержит два члена; один из них 5x, содержащий неизвестный множитель x, можно назвать неизвестным членом, а другой –7 – известным. Во второй части уравнения также 2 члена: неизвестный 4x и известный +15. Сделаем так, чтобы в левой части уравнения оказались только неизвестные члены (а известный член –7 уничтожился бы), а в правой части оказались бы только известные члены (а неизвестный член +4x уничтожился бы). Для этой цели прибавим к обеим частям уравнения одинаковые числа: 1) прибавим по +7 (чтобы уничтожился член –7) и 2) прибавим по –4x (чтобы уничтожился член +4x). Тогда получим:

5x – 7 + 7 – 4x = 4x + 15 + 7 – 4x

Сделав в каждой части уравнения приведение подобных членов, получим

Это равенство и является решением уравнения, так как оно указывает, что для x надо взять число 22.

Пример 2. Решить уравнение:

Опять прибавим к обеим частям уравнения по –11 и по +4x, получим:

8x + 11 – 11 + 4x = 7 – 4x – 11 + 4x

Выполнив приведение подобных членов, получим:

Разделим теперь обе части уравнения на +12, получим:

x = –4/12 или x = –1/3

(первую часть уравнения 12x разделить на 12 – получим 12x/12 или просто x; вторую часть уравнения –4 разделить на +12 – получим –4/12 или –1/3).

Последнее равенство и является решением уравнения, так как оно указывает, что для x надо взять число –1/3.

Пример 3. Решить уравнением

x – 23 = 3 · (2x – 3)

Раскроем сначала скобки, получим:
x – 23 = 6x – 9

Прибавим к обеим частям уравнения по +23 и по –6x, – получим:

x – 23 + 23 – 6x = 6x – 9 + 23 – 6x.

Теперь, для того, чтобы впоследствии ускорить процесс решения уравнения, не будем сразу выполнять приведение всех подобных членов, а только заметим, что члены –23 и +23 в левой части уравнения взаимно уничтожаются, также члены +6x и –6x в первой части взаимно уничтожаются – получим:

Сравним это уравнение с начальным: вначале было уравнение:

Теперь получили уравнение:

Мы видим, что в конце концов оказалось, что член –23, находившийся сначала в левой части уравнения, теперь как бы перешел в правую часть уравнения, причем у него переменился знак (в левой части начального уравнения был член –23, теперь его там нет, но зато в правой части уравнения имеется член + 23, которого там раньше не было). Так же точно в правой части уравнения был член +6x, теперь его там нет, но появился зато в левой части уравнения член –6x, которого раньше там не было. Рассматривая с этой точки зрения примеры 1 и 2, мы придем к общему заключению:

Можно любой член уравнения перенести из одной части в другую, меняя знак у этого члена (в дальнейших примерах мы будем этим пользоваться).

Итак, возвращаясь к нашему примеру, мы получили уравнение

Выполним приведение подобных членов:

Разделим обе части уравнения на –5. Тогда получим:

[–5x : (–5) получим x] – это и есть решение нашего уравнения.

Пример 4. Решить уравнение:

Сделаем так, чтобы в уравнении не было дробей. Для этой цели найдем общего знаменателя для наших дробей – общим знаменателем служит число 24 – и умножим на него обе части нашего уравнения (можно, ведь, чтобы равенство не нарушалось, умножить на одно и то же число только обе части уравнения). В первой части 3 члена, причем каждый член является дробью — надо, следовательно, каждую дробь умножить на 24: вторая часть уравнения есть 0, а нуль умножить на 24 — получим нуль. Итак,

Мы видим, что каждая из наших трех дробей, благодаря тому, что она умножена на общее наименьшее кратное знаменателей этих дробей, сократится и сделается целым выражением, а именно получим:

(3x – 8) · 4 – (2x – 1) · 6 + (x – 7) · 3 = 0

Конечно, желательно все это выполнить в уме: надо вообразить, что, например, числитель первой дроби заключается в скобки и умножается на 24, после чего воображение поможет нам увидеть сокращение это дроби (на 6) и конечный результат, т. е. (3x – 8) · 4. Тоже имеет место и для остальных дробей. Раскроем теперь в полученном уравнении (в его левой части) скобки:

12x – 32 – 12x + 6 + 3x – 21 = 0

(обратим внимание, что здесь понадобилось двучлен 2x – 1 умножить на 6 и полученное произведение 12x – 6 вычесть из предыдущего, благодаря чему знаки членов этого произведения должны перемениться — выше и написано –12x + 6). Перенесем известные члены (т. е. –32, +6 и –21) из левой части уравнения в его правую часть, причем (как мы уже знаем) знаки этих членов должны перемениться — получим:

12x – 12x + 3x = 32 – 6 + 21.

Выполним приведение подобных членов:

(при навыке должно сразу выполняться и перенесение нужных членов из одной части уравнения в другую и приведение подобных членов), разделим, наконец, обе части уравнения на 3 — получим:

x = 15(2/3) — это и есть решение уравнения.

Пример 5. Решить уравнение:

5 – (3x + 1)/7 = x + (2x – 3)/5

Здесь две дроби, и их общий знаменатель равен 35. Умножим, чтобы освободить уравнение от дробей, обе части уравнения на общего знаменателя 35. В каждой части нашего уравнения 2 члена. При умножении каждой части на 35 должно каждый член умножить на 35 — получим:

Дроби сократятся — получим:

175 – (3x + 1) · 5 = 35x + (2x – 3) · 7

(конечно, можно было бы при навыке написать сразу это уравнение).

Выполним все действия:

175 – 15x – 5 = 35x + 14x – 21.

Перенесем все неизвестные члены из правой части (т. е. члены +35x и +14x) в левую, а все известные члены из левой части (т. е. члены +175 и –5) в правую — следует при этом не забывать у переносимых членов менять знак:

–15x – 35x – 14x = –21 – 175 + 5

(член –15x, как раньше был в левой части, так и теперь в ней остался — у него поэтому отнюдь не следует менять знака; аналогичное имеет место и для члена –21). Сделав приведение подобных членов, получим:

[Возможно сделать так, чтобы не было знака минус в обеих частях уравнения; для этого умножим обе части уравнения на (–1), получим 64x = 191, но этого можно и не делать.]
Разделим затем обе части уравнения на (–64), получим решение нашего уравнения

[Если умножили обе части уравнения на (–1) и получили уравнение 64x = 191, то теперь надо обе части уравнения разделить на 64.]

На основании того, что пришлось выполнять в примерах 4 и 5, мы можем установить: можно освободить уравнение от дробей — для этого надо найти общего знаменателя для всех дробей, входящих в уравнение (или наименьшее общее кратное знаменателей всех дробей) и на него умножить обе части уравнения — тогда дроби должны исчезнуть.

Пример 6. Решить уравнение:

Перенеся член 4x из правой части уравнения в левую, получим:

5x – 4x = 0 или x = 0.

Итак, решение найдено: для x надо взять число нуль. Если мы заменим в данном уравнении x нулем, получим 5 · 0 = 4 · 0 или 0 = 0, что указывает на выполнение требования, выражаемого данным уравнением: найти такое число для x, чтобы одночлен 5x оказался равен тому же самому числу, как и одночлен 4x.

Если кто-либо подметит с самого начала, что обе части уравнения 5x = 4x можно разделить на x и выполнит это деление, то получится явная несообразность 5 = 4! Причиною этого является то обстоятельство, что деление 5x/x в данном случае выполнить нельзя, так как, мы видели выше, вопрос, выражаемый нашим уравнением, требует, чтобы x = 0, а деление на нуль не выполнимо.

Заметим еще, что и умножение на нуль требует некоторой внимательности: умножая на нуль и два неравных числа, мы получим в результате этих умножений равные произведения, а именно — нули.

Если, например, мы имеем уравнение

x – 3 = 7 – x (его решение: x = 5)

и если кто-либо захочет к нему применить свойство «обе части уравнения можно умножить на одно и тоже число» и умножить обе части на x, то получит:

x 2 – 3x = 7x – x 2 .

После этого может обратить на себя внимание, что все члены уравнения содержат множителя x, из чего можно сделать заключение, что для решения этого уравнения можно взять число нуль, т. е. положить x = 0. И в самом деле, тогда получим:
0 2 – 3 · 0 = 7 · 0 – 0 2 или 0 = 0.

Однако, это решение x = 0, очевидно, не годится для данного уравнения x – 3 = 7 – x; заменяя в нем x нулем, получим явную несообразность: 3 = 7!