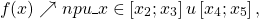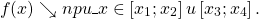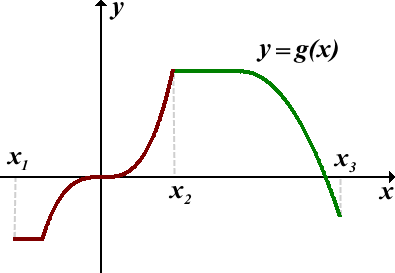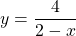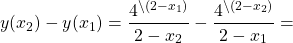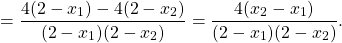О чем эта статья:
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Математика
- Тестирование онлайн
- Определение. График
- Свойства линейной функции
- Особые случаи
- Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
- теория по математике 📈 функции
- Нули функции
- Промежутки знакопостоянства
- Возрастание и убывание функции
- Когда функция возрастает а когда убывает в уравнение
- Возрастание и убывание функций
- Возрастание и убывание функции на интервале, экстремумы
- Возрастание и убывание функции на интервале
- Точки экстремума, экстремумы функции
- Достаточные условия возрастания и убывания функции
- Первое достаточное условие экстремума
- Алгоритм для нахождения точек экстремума
- Второй признак экстремума функции
- Третье достаточное условие экстремума
- Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
- теория по математике 📈 функции
- Нули функции
- Промежутки знакопостоянства
- Возрастание и убывание функции
Видео:АЛГЕБРА 9 класс. Возрастающая и убывающая функцииСкачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Как доказать, что функция убывает или возрастаетСкачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
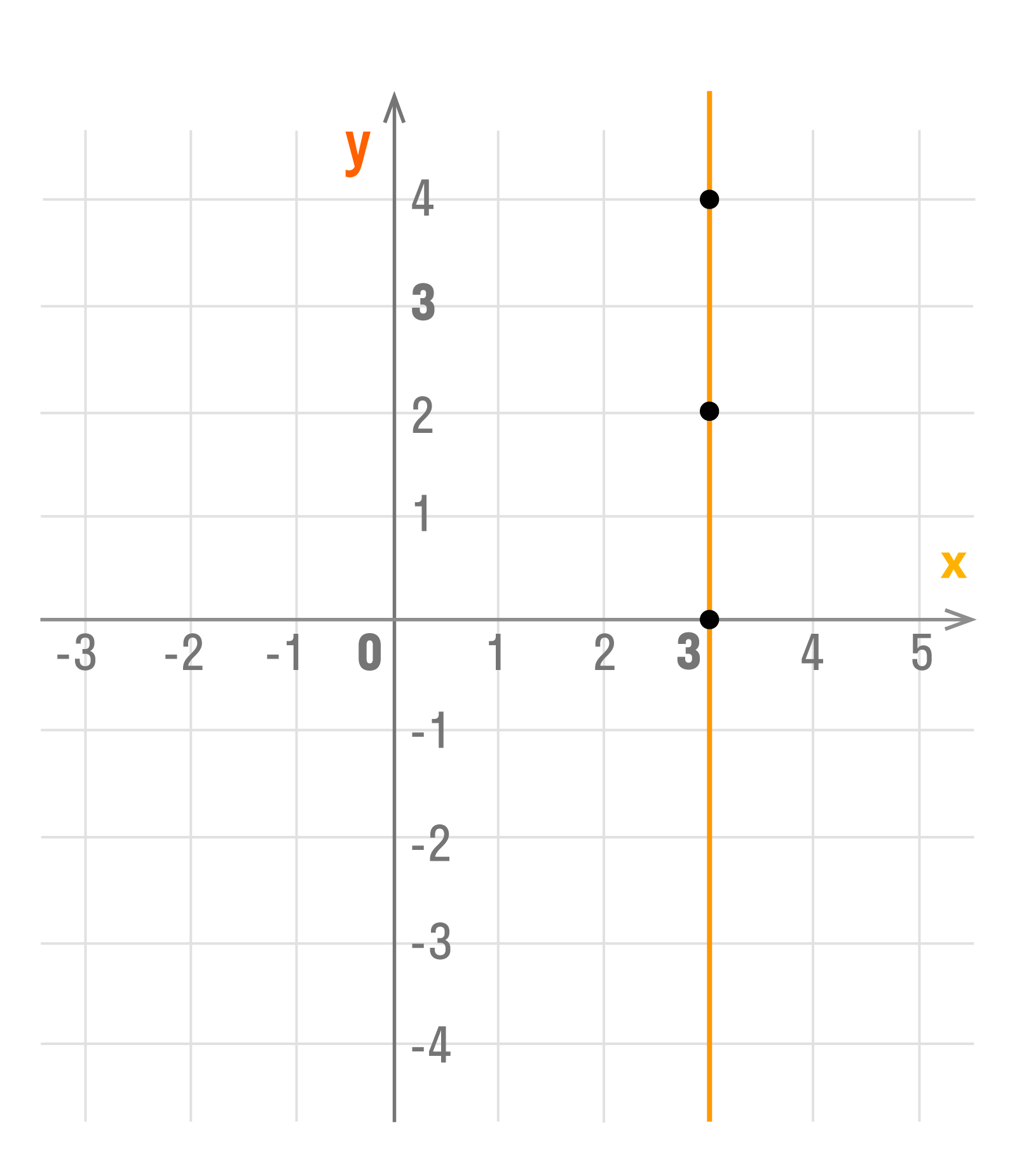
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:Возрастание функции | убывание функции | 9 класс МакарычевСкачать
Математика
Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Тестирование онлайн
Видео:Промежутки возрастания и убывания функции. 10 класс.Скачать

Определение. График
Линейной функцией называется функция вида
где k, b — некоторые числа.
Функция вида 
Графиком линейной функции является прямая линия.
Для построения графика достаточно знать координаты двух точек.
Видео:Как решать линейные уравнения #математика #математика7классСкачать

Свойства линейной функции
1) Область определения функции — множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке 
7) 
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k 0: функция принимает отрицательные значения на промежутке 
При k 0, то этот угол острый, если k <0— тупой, если k=0, то прямая совпадает с осью Ох.
Для построения графика функции — прямой линии, очевидно, достаточно двух точек.

Видео:7 класс. Алгебра. Линейная функция. Возрастающая и убывающая. Коэффициент k.Скачать

Особые случаи
1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.

2) Если k=0, получим уравнение y=b. Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
График функции у=k/x выглядит следующим образом: 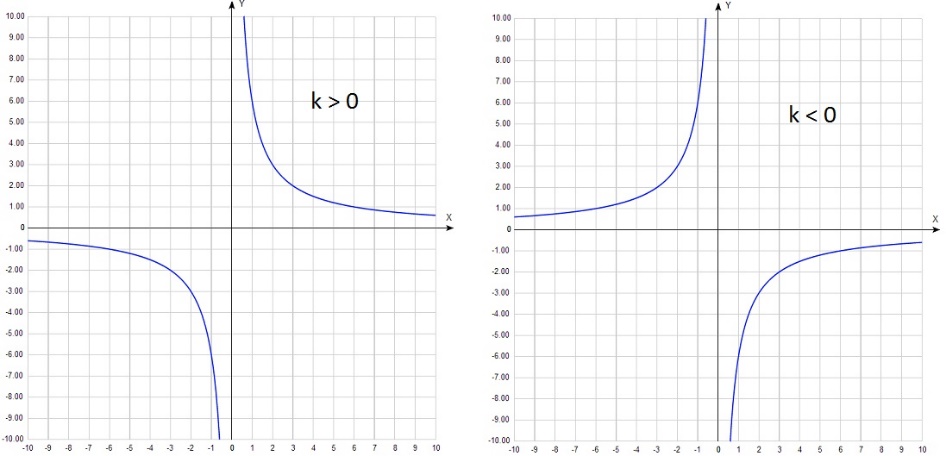
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
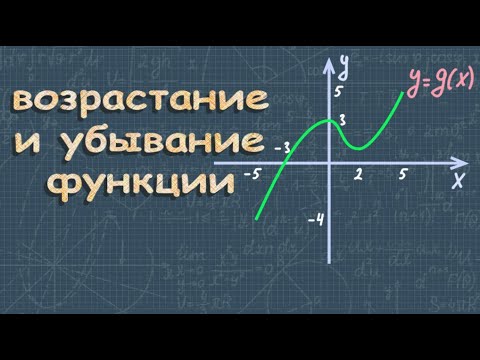
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Когда функция возрастает а когда убывает в уравнение
Видео:Задание 10 Квадратичная функция Промежутки возрастания убыванияСкачать
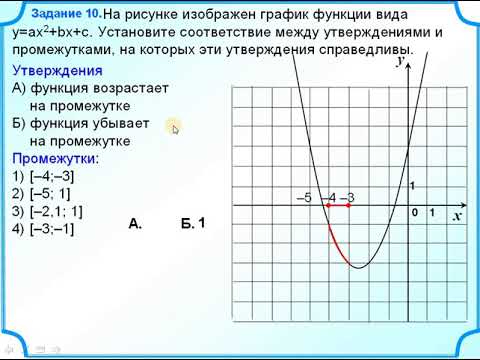
Возрастание и убывание функций
1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
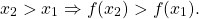
2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
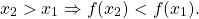
Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.
График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).
На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).
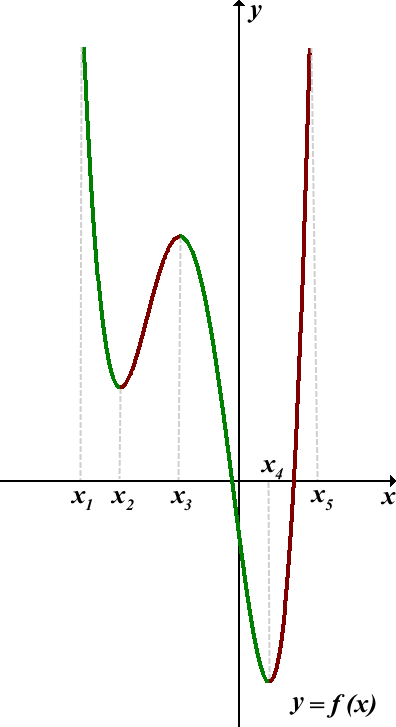
Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x1;x5]:
Кратко это записывают так:
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).
4) Если функция возрастает на всей своей области определения, то её называют возрастающей.
Если функция убывает на всей своей области определения, то её называют убывающей.
Например, y=√x, y=x³ — возрастающие функции.
Линейная функция y=kx+b возрастающая при k>0 и убывающая при k 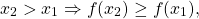
то функция y=f(x) называется неубывающей на этом промежутке.
6) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
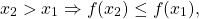
то функция y=f(x) называется невозрастающей на этом промежутке.
7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.
Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x1;x3], является невозрастающей и неубывающей:
Функция y=g(x) является неубывающей на промежутке [x1;x2].
Функция y=g(x) является невозрастающей на промежутке [x2;x3].
Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.
Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?
группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:
Теперь выносим общий множитель (x2-x1) за скобки:
Так как x2>x1, то x2-x1>0. Следовательно, знак произведения зависит от знака второго множителя.
Для x1, x2 ∈(-∞;-2) x2+x1+4
возрастает на промежутке (2;+∞).
Функция определена при x∈(-∞;2) и (2;+∞).
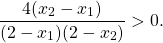
Отсюда y(x2)-y(x1)>0. Поэтому данная функция возрастает на промежутке (2;+∞).
Что и требовалось доказать.
Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).
Видео:13A.1 Найдите промежутки возрастания и убывния функции f(x), заданной графикомСкачать
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Видео:Как решать линейные уравнения?Скачать

Возрастание и убывание функции на интервале
Функция y = f ( x ) будет возрастать на интервале x , когда при любых x 1 ∈ X и x 2 ∈ X , x 2 > x 1 неравенство f ( x 2 ) > f ( x 1 ) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y = f ( x ) считается убывающей на интервале x , когда при любых x 1 ∈ X , x 2 ∈ X , x 2 > x 1 равенство f ( x 2 ) > f ( x 1 ) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.
Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть ( a ; b ) , где х = а , х = b , точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x .
Основные свойства элементарных функций типа y = sin x – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале — π 2 ; π 2 , тогда возрастание на отрезке имеет вид — π 2 ; π 2 .
Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Точки экстремума, экстремумы функции
Точка х 0 называется точкой максимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≥ f ( x ) является справедливым. Максимум функции – это значение функции в точке, причем обозначается y m a x .
Точка х 0 называется точкой минимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≤ f ( x ) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида y m i n .
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [ a ; b ] . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Первое достаточное условие экстремума
Пусть задана функция y = f ( x ) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что
- когда f ‘ ( x ) > 0 с x ∈ ( x 0 — ε ; x 0 ) и f ‘ ( x ) 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой максимума;
- когда f ‘ ( x ) 0 с x ∈ ( x 0 — ε ; x 0 ) и f ‘ ( x ) > 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на — , значит, точка называется максимумом;
- когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с — на + , значит, точка называется минимумом.
Видео:ГРАФИК ФУНКЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y = 2 ( x + 1 ) 2 x — 2 .
Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:
y ‘ = 2 x + 1 2 x — 2 ‘ = 2 · x + 1 2 ‘ · ( x — 2 ) — ( x + 1 ) 2 · ( x — 2 ) ‘ ( x — 2 ) 2 = = 2 · 2 · ( x + 1 ) · ( x + 1 ) ‘ · ( x — 2 ) — ( x + 1 ) 2 · 1 ( x — 2 ) 2 = 2 · 2 · ( x + 1 ) · ( x — 2 ) — ( x + 2 ) 2 ( x — 2 ) 2 = = 2 · ( x + 1 ) · ( x — 5 ) ( x — 2 ) 2
Отсюда видим, что нули функции – это х = — 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:
Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = — 2 , х = 0 , х = 3 , х = 6 .
y ‘ ( — 2 ) = 2 · ( x + 1 ) · ( x — 5 ) ( x — 2 ) 2 x = — 2 = 2 · ( — 2 + 1 ) · ( — 2 — 5 ) ( — 2 — 2 ) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал — ∞ ; — 1 имеет положительную производную. Аналогичным образом получаем, что
y ‘ ( 0 ) = 2 · ( 0 + 1 ) · 0 — 5 0 — 2 2 = 2 · — 5 4 = — 5 2 0 y ‘ ( 3 ) = 2 · ( 3 + 1 ) · ( 3 — 5 ) ( 3 — 2 ) 2 = 2 · — 8 1 = — 16 0 y ‘ ( 6 ) = 2 · ( 6 + 1 ) · ( 6 — 5 ) ( 6 — 2 ) 2 = 2 · 7 16 = 7 8 > 0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х = — 1 функция будет непрерывна, значит, производная изменит знак с + на — . По первому признаку имеем, что х = — 1 является точкой максимума, значит получаем
y m a x = y ( — 1 ) = 2 · ( x + 1 ) 2 x — 2 x = — 1 = 2 · ( — 1 + 1 ) 2 — 1 — 2 = 0
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
y m i n = y ( 5 ) = 2 · ( x + 1 ) 2 x — 2 x = 5 = 2 · ( 5 + 1 ) 2 5 — 2 = 24
Ответ: y m a x = y ( — 1 ) = 0 , y m i n = y ( 5 ) = 24 .
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.
Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x — 8 .
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
— 1 6 x 3 — 2 x 2 — 22 3 x — 8 , x 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 , x ≥ 0
После чего необходимо найти производную:
y ‘ = 1 6 x 3 — 2 x 2 — 22 3 x — 8 ‘ , x 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 ‘ , x > 0 y ‘ = — 1 2 x 2 — 4 x — 22 3 , x 0 1 2 x 2 — 4 x + 22 3 , x > 0
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y ‘ x → 0 — 0 = lim y x → 0 — 0 — 1 2 x 2 — 4 x — 22 3 = — 1 2 · ( 0 — 0 ) 2 — 4 · ( 0 — 0 ) — 22 3 = — 22 3 lim y ‘ x → 0 + 0 = lim y x → 0 — 0 1 2 x 2 — 4 x + 22 3 = 1 2 · ( 0 + 0 ) 2 — 4 · ( 0 + 0 ) + 22 3 = + 22 3
Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем
lim y x → 0 — 0 = lim x → 0 — 0 — 1 6 x 3 — 2 x 2 — 22 3 x — 8 = = — 1 6 · ( 0 — 0 ) 3 — 2 · ( 0 — 0 ) 2 — 22 3 · ( 0 — 0 ) — 8 = — 8 lim y x → 0 + 0 = lim x → 0 — 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 = = 1 6 · ( 0 + 0 ) 3 — 2 · ( 0 + 0 ) 2 + 22 3 · ( 0 + 0 ) — 8 = — 8 y ( 0 ) = 1 6 x 3 — 2 x 2 + 22 3 x — 8 x = 0 = 1 6 · 0 3 — 2 · 0 2 + 22 3 · 0 — 8 = — 8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
— 1 2 x 2 — 4 x — 22 3 , x 0 D = ( — 4 ) 2 — 4 · — 1 2 · — 22 3 = 4 3 x 1 = 4 + 4 3 2 · — 1 2 = — 4 — 2 3 3 0 x 2 = 4 — 4 3 2 · — 1 2 = — 4 + 2 3 3 0
1 2 x 2 — 4 x + 22 3 , x > 0 D = ( — 4 ) 2 — 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 — 4 3 2 · 1 2 = 4 — 2 3 3 > 0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = — 6 , x = — 4 , x = — 1 , x = 1 , x = 4 , x = 6 . Получим, что
y ‘ ( — 6 ) = — 1 2 x 2 — 4 x — 22 3 x = — 6 = — 1 2 · — 6 2 — 4 · ( — 6 ) — 22 3 = — 4 3 0 y ‘ ( — 4 ) = — 1 2 x 2 — 4 x — 22 3 x = — 4 = — 1 2 · ( — 4 ) 2 — 4 · ( — 4 ) — 22 3 = 2 3 > 0 y ‘ ( — 1 ) = — 1 2 x 2 — 4 x — 22 3 x = — 1 = — 1 2 · ( — 1 ) 2 — 4 · ( — 1 ) — 22 3 = 23 6 0 y ‘ ( 1 ) = 1 2 x 2 — 4 x + 22 3 x = 1 = 1 2 · 1 2 — 4 · 1 + 22 3 = 23 6 > 0 y ‘ ( 4 ) = 1 2 x 2 — 4 x + 22 3 x = 4 = 1 2 · 4 2 — 4 · 4 + 22 3 = — 2 3 0 y ‘ ( 6 ) = 1 2 x 2 — 4 x + 22 3 x = 6 = 1 2 · 6 2 — 4 · 6 + 22 3 = 4 3 > 0
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x = — 4 — 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = — 4 + 2 3 3 , x = 4 — 2 3 3
Перейдем к вычислению минимумов:
y m i n = y — 4 — 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = — 4 — 2 3 3 = — 8 27 3 y m i n = y ( 0 ) = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 0 = — 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 4 + 2 3 3 = — 8 27 3
Произведем вычисления максимумов функции. Получим, что
y m a x = y — 4 + 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = — 4 + 2 3 3 = 8 27 3 y m a x = y 4 — 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 4 — 2 3 3 = 8 27 3
y m i n = y — 4 — 2 3 3 = — 8 27 3 y m i n = y ( 0 ) = — 8 y m i n = y 4 + 2 3 3 = — 8 27 3 y m a x = y — 4 + 2 3 3 = 8 27 3 y m a x = y 4 — 2 3 3 = 8 27 3
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Второй признак экстремума функции
Если задана функция f ‘ ( x 0 ) = 0 , тогда при ее f » ( x 0 ) > 0 получаем, что x 0 является точкой минимума, если f » ( x 0 ) 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .
Найти максимумы и минимумы функции y = 8 x x + 1 .
Для начала находим область определения. Получаем, что
D ( y ) : x ≥ 0 x ≠ — 1 ⇔ x ≥ 0
Необходимо продифференцировать функцию, после чего получим
y ‘ = 8 x x + 1 ‘ = 8 · x ‘ · ( x + 1 ) — x · ( x + 1 ) ‘ ( x + 1 ) 2 = = 8 · 1 2 x · ( x + 1 ) — x · 1 ( x + 1 ) 2 = 4 · x + 1 — 2 x ( x + 1 ) 2 · x = 4 · — x + 1 ( x + 1 ) 2 · x
При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:
y » = 4 · — x + 1 ( x + 1 ) 2 · x ‘ = = 4 · ( — x + 1 ) ‘ · ( x + 1 ) 2 · x — ( — x + 1 ) · x + 1 2 · x ‘ ( x + 1 ) 4 · x = = 4 · ( — 1 ) · ( x + 1 ) 2 · x — ( — x + 1 ) · x + 1 2 ‘ · x + ( x + 1 ) 2 · x ‘ ( x + 1 ) 4 · x = = 4 · — ( x + 1 ) 2 x — ( — x + 1 ) · 2 x + 1 ( x + 1 ) ‘ x + ( x + 1 ) 2 2 x ( x + 1 ) 4 · x = = — ( x + 1 ) 2 x — ( — x + 1 ) · x + 1 · 2 x + x + 1 2 x ( x + 1 ) 4 · x = = 2 · 3 x 2 — 6 x — 1 x + 1 3 · x 3 ⇒ y » ( 1 ) = 2 · 3 · 1 2 — 6 · 1 — 1 ( 1 + 1 ) 3 · ( 1 ) 3 = 2 · — 4 8 = — 1 0
Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y ( 1 ) = 8 1 1 + 1 = 4 .
Ответ: y m a x = y ( 1 ) = 4 ..
Третье достаточное условие экстремума
Функция y = f ( x ) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f ‘ ( x 0 ) = f » ( x 0 ) = f ‘ ‘ ‘ ( x 0 ) = . . . = f n ( x 0 ) = 0 .
Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f ( n + 1 ) ( x 0 ) > 0 , тогда x 0 является точкой минимума, f ( n + 1 ) ( x 0 ) 0 , тогда x 0 является точкой максимума.
Найти точки максимума и минимума функции y y = 1 16 ( x + 1 ) 3 ( x — 3 ) 4 .
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y ‘ = 1 16 x + 1 3 ‘ ( x — 3 ) 4 + ( x + 1 ) 3 x — 3 4 ‘ = = 1 16 ( 3 ( x + 1 ) 2 ( x — 3 ) 4 + ( x + 1 ) 3 4 ( x — 3 ) 3 ) = = 1 16 ( x + 1 ) 2 ( x — 3 ) 3 ( 3 x — 9 + 4 x + 4 ) = 1 16 ( x + 1 ) 2 ( x — 3 ) 3 ( 7 x — 5 )
Данная производная обратится в ноль при x 1 = — 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y » = 1 16 x + 1 2 ( x — 3 ) 3 ( 7 x — 5 ) ‘ = 1 8 ( x + 1 ) ( x — 3 ) 2 ( 21 x 2 — 30 x — 3 ) y » ( — 1 ) = 0 y » 5 7 = — 36864 2401 0 y » ( 3 ) = 0
Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f ( n + 1 ) 5 7 0 .
Необходимо определить характер точек x 1 = — 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y ‘ ‘ ‘ = 1 8 ( x + 1 ) ( x — 3 ) 2 ( 21 x 2 — 30 x — 3 ) ‘ = = 1 8 ( x — 3 ) ( 105 x 3 — 225 x 2 — 45 x + 93 ) y ‘ ‘ ‘ ( — 1 ) = 96 ≠ 0 y ‘ ‘ ‘ ( 3 ) = 0
Значит, x 1 = — 1 является точкой перегиба функции, так как при n = 2 и f ( n + 1 ) ( — 1 ) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:
y ( 4 ) = 1 8 ( x — 3 ) ( 105 x 3 — 225 x 2 — 45 x + 93 ) ‘ = = 1 2 ( 105 x 3 — 405 x 2 + 315 x + 57 ) y ( 4 ) ( 3 ) = 96 > 0
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 — точкой минимума заданной функции.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
График функции у=k/x выглядит следующим образом: 
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.