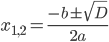Коэффициенты a b c квадратного уравнения ax2 bx c 0 в указанном порядке являются (2 видео)

Квадратное уравнение

Квадратное уравнение ax 2 + bx + c = 0 на C++ лучше всего решать с помощью формулы, содержащей дискриминант:

Разберем пример кода такой программы:

Данная программа учитывает все исходы при решении подобного уравнения.

Содержание

Похожие записи:
Квадратное уравнение: 8 комментариев
Коэффициенты a b c квадратного уравнения ax2 bx c 0 в указанном порядке являются
Квадратное уравнение. Дискриминант. Теорема Виета.
теория по математике 📈 уравнения
Дискриминант
Теорема Виета
Квадратные уравнения (способы решения)
💡 Видео

Квадратное уравнение: 8 комментариев

Добрый день! А как быть со случаями, когда а == 0; b == 0 && c > 0; b == 0 && C !=0 и т.д.?

При a == 0 уравнение перестает называться квадратным. Проблемы также возникают, когда, например, пользователь ввел букву вместо числа. Такие случаи называются аномалиями.
Все аномалии рассмотреть нельзя. Если требуется, то можно, например, рассмотреть аномалию a == 0, добавив после 11-й строки:
if (a == 0)
<
cout

«Все аномалии рассмотреть нельзя.»
Сложно с Вами согласиться. Не такая уж это и нетривиальная задача для программиста — решить уравнение ax2 + bx + c = 0 на C++, учтя все возможные варианты а, b, c, в том числе и когда уравнение перестает быть квадратным и другие.
В противном случае код получается не универсальный, а только для некоторых случаев, когда переменные Вас «устраивают».
Согласитесь — это не решение задачи, а нахождение решения для группы частных случаев.

Нельзя. Будет всегда компьютер, бракованный, на котором программа не будет работать. На этом факте основано всё лицензирование программного обеспечения. Бракованный компьютер — тоже совокупность аномалий.

По квадратному уравнению имеет смысл рассматривать аномалии только, если от Вас это требуется в задании. И процесс такой длительный:
1. Рассматриваются случаи, когда пользователь ввел уравнение, не являющееся квадратным.
2. Рассматриваются случаи, когда пользователь ввел a,b,c, не являющиеся числами.
3. Рассматриваются случаи, когда пользователь, не умеет запускать программу, пишется инструкция.
4. Рассматриваются случаи, когда пользователь не умеет читать, пишется инструкция с картинками, часто с голосовым помощником.
5. Это именно программа, поэтому можно также составить инструкцию по компиляции, указать различные версии программы для разных стандартов языка.
.
Это все не моя выдумка, так делают, но только, если это действительно нужно.

Бывает другой случай, например, нужно сдать программу, решающую квадратное уравнение, преподавателю и вот здесь нужно сделать минимум, то, что написано в примере, а дальше, только если преподаватель просит.

Нет. Вы не правы.
Про аномалии — я вообще ничего не говорю. Я говорю только про задачу, которую озвучили Вы: решить ax2 + bx + c = 0. Другими словами — найти все возможные ответы при абсолютно любых значениях а, b и с. Без исключений. Не важно — квадратное будет уравнение или линейное, после того, как мы с консоли введем переменные. В этом весь смысл программирования. Сделать универсальное решение, которое будет работать всегда, при любых значениях переменных (аномалии, когда пользователю оторвало руки и он не может ввести переменные с консоли, истекая кровью, я тоже не рассматриваю).
Глупо, имея инструмент, который позволяет решить задачу, не решать её в любых, без исключения, случаях. А ограничивать себя только удобными случаями и тривиальными. Это не программирование получается, а ерунда какая-то, решение частных случаев. «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. »
Вот, корявый, конечно, не оптимальный, но работающий во всех случаях код:

#include
#include
using namespace std;

int main() <
double a, b, c;
cin >> a >> b >> c;
/*(D = b*b minus 4*a*c) — считаем дискриминант*/
double d = (b*b) — 4 * a * c;
double x1, x2, d1;
d1=sqrt(d);/*корень из дискриминанта — заготовка для решения решаемого квадратного уравнения*/
/*1. группируем все исключения — когда решение вообще или через дискриминант невозможно*/
/*2. в каждое исключение сливаем все условия и для этих условий пишем вывод*/
/*3. оставшиеся случаи решаем через дискриминант*/
if ((a==0 && b == 0 ) || ( b==0 && ((c> 0 && a>0) || (c

Про аномалии это я переделал. Лучше говорить аномалии, а не исключения.
Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.
Посмотрите математическую энциклопедию.

Ещё раз повторю: Вы не сможете сделать универсальное решение, которое будет работать всегда.

Ваше решение просто лучше моего, оно не работает, если вместо a, я ввожу rrr или другие символы.

Аномалии про оторванные руки и кровь тоже рассматривают, есть даже задачи и модели математические про ситуацию, когда 0 взял так и случайно стал 1 в памяти ЭВМ. Про глупость, ну а что, так и есть, глупость это нормально. Ваша программа умнее моей.

Это не ерунда, а программирование. Первый этап, который всегда должен происходить, это спецификация (уточнение) задачи. Пишется такая бумага, в которой как раз и есть «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. «.

Вопрос у Вас фактически про спецификацию (уточнение). Те пять пунктов, которые я в предыдущем комментарии написал — совершенно адекватные требования преподавателя, заказчика, сайта с хранилищем программного обеспечения. Часто преподаватели говорят — составить отчёт с инструкциями даже по такой программе как решение квадратного уравнения, это нормально. Про оторванные руки я не писал как раз как про первоочередную задачу.

Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена. Если требуют уточнить, нужно уметь уточнять. Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.

Математической энциклопедии под рукой не нашлось.
«Лучше говорить аномалии, а не исключения.»
Не помню из курса алгебры (в рамках которой изучается решение квадратных уравнений) такого термина — аномалии, но допускаю, что Вы правы и такой математический термин существует и его можно применить к квадратному уравнению.
«Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.»
Прочитал внимательно. «ax2 + bx + c = 0» — где сказано, что а не равен нулю?
«Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена.»
Когда я пытался пропихнуть код, который не учитывает исключений — не приняли, хотя вот текст моего задания:
«На вход вашей программы в стандартном потоке ввода подаются действительные коэффициенты A, B и C уравнения Ax² + Bx + C = 0. Выведите все его различные действительные корни в поток вывода в любом порядке, при этом разделяя корни пробелами. Гарантируется, что хотя бы один из коэффициентов уравнения не равен нулю.»
«Вы не сможете сделать универсальное решение, которое будет работать всегда.» и «Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.»
Позвольте, Вы настаиваете, что невозможно написать код, который будет решать квадратное уравнение при любых действительных a, b и c? Как-то можете теоретически аргументировать? Пока что только не подкрепленные утверждения, не готов принимать их на веру.
При каких действительных значениях а, b и c мой, реально корявый, код не работает?

Страницы математических энциклопедий доступны через Яндекс. Только внимательнее, там есть поясняющие материалы в результатах поиска, не перепутайте.

Квадратное уравнение — алгебраическое уравнение 2-й степени. Общий вид К. у. ax^+bx+c=0, a != 0.

Что такое аномалия?
В тестировании программного обеспечения под аномалией понимается результат, отличный от ожидаемого. Такое поведение может быть результатом документа а также представлений и опыта тестировщиков.

Аномалия может также относиться к проблеме удобства использования, поскольку тестовое программное обеспечение может вести себя в соответствии со спецификацией, но удобство его использования все же можно улучшить. Иногда аномалия также может быть названа дефектом / ошибкой.

Перед тем как разрабатывать программу проводят формальную спецификацию (уточнение) задания.

В информатике формальная спецификация — это математическое описание программной или аппаратной системы, которая может быть реализована в соответствии с этим описанием. Специфицируется, что должна делать система, но не то, как она должна это делать.

Если система огромная — длительное обсуждение, анализ и т.д. Для небольших программ, вот как решение квадратного уравнения, можно на бумаге составить. Вот на этой бумаге пишется задача, ИД — исходные данные, ВД — выходные данные, реакция на аномалии и т.д. В пункте реакция на аномалии рисуется таблица, по крайней мере с двумя столбцами: название аномалии, то что программа будет в этом случае делать.

У Вас в задании слова квадратное как раз нет и аккуратно написано, что подаются только действительные числа. Формальная спецификация выполнена в задании в основном.

Если будут вводить только действительные числа, можно написать работающий код. По такой формальной спецификации можно, я почти уверен, хотя доказательства корректности работы программы трудные.

Нельзя написать универсальное решение, без аномалий, на все случаи жизни. Тот же потенциальный пользователь программы решения квадратного уравнения, школьник, будет тыкать во всю клавиатуру, а не только в цифры.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Коэффициенты a b c квадратного уравнения ax2 bx c 0 в указанном порядке являются

Этот способ решения помогает не только сэкономить время, но и развить внимание.

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a + b + c = 0 (сумма коэффициентов), то

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a — b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то

341x 2 + 290x — 51 = 0

Здесь, a = 341, b = 290, c = -51.

Проверим удовлетворяют ли коэффициенты условию

341 — 51 = 290. Получим а + с = b. Следовательно, мы

можем воспользоваться свойством 2.

Если в квадратном уравнении ax 2 + bx + c = 0 . Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Квадратные уравнения (способы решения)

Разделы: Математика

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.

Определение

Уравнение вида ax 2 + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.

Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.

Корни уравнения ax 2 + bx + c = 0 находят по формуле

Коэффициенты a b c квадратного уравнения ax2 bx c 0 в указанном порядке являются

Выражение D = b 2 — 4ac называют дискриминантом квадратного уравнения.

если D 0, то уравнение имеет два действительных корня.

В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Формулы

Полное квадратное уравнение

Неполные квадратные уравнения

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

Решение неполного квадратного уравнения

Квадратные уравнения с комплексными переменными

Сначала рассмотрим простейшее квадратное уравнение z 2 = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:

имеет один корень z = 0, если а = 0;
имеет два действительных корня z_{1, 2} = ±√a
Не имеет действительных корней, если a 2 + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x 2 ; y = x + 1.

y = x 2 , квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.

Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.

Решение задач с помощью квадратных уравнений

Процессы	Скорость км/ч	Время ч.	Расстояние км.
Вверх по реке	10 — x	35 / (10 — x)	35
Вверх по протоку	10 — x + 1	18 / (10 — x + 1)	18
V течения	x
V притока	x + 1