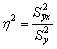Коэффициентом детерминации r2 характеризует долю вариации переменной с помощью уравнения регрессии

Нет времени или сил пройти тест онлайн? Поможем сдать тест дистанционно для любого учебного заведения: подробности.

Вопрос 1. Статистической зависимостью называется …

• точная формула, связывающая переменные
• связь переменных без учета воздействия случайных факторов
• связь переменных, на которую накладывается воздействие случайных факторов
• любая связь переменных

Вопрос 2. Универсальным способом задания случайной величины Х является задание ее … распределения

Вопрос 3. Дискретной называется случайная величина, …

• множество значений которой заполняет числовой промежуток
• которая задается плотностью распределения
• которая задается полигоном распределения
• которая принимает отдельные, изолированные друг от друга значения

Вопрос 4. Выборочная средняя является …

• несмещенной оценкой генеральной дисперсии
• несмещенной оценкой генеральной средней
• смещенной оценкой генеральной средней
• смещенной оценкой генеральной дисперсии

Вопрос 5. Выборочная дисперсия является …

• смещенной оценкой генеральной дисперсии
• несмещенной оценкой генеральной дисперсии
• несмещенной оценкой генеральной средней
• смещенной оценкой генеральной средней

Вопрос 6. В модели парной линейной регрессии величина У является …

• неслучайной
• постоянной
• случайной
• положительной

Вопрос 7. В модели парной линейной регрессии величина ? является …

• случайной
• неслучайной
• положительной
• постоянной

Вопрос 8. Предположение о нормальности распределения случайного члена необходимо для …

• расчета коэффициента детерминации
• проверки значимости коэффициента детерминации
• проверки значимости параметров регрессии и для их интервального оценивания
• расчета параметров регрессии

Вопрос 9. Эконометрика – наука, изучающая …

• проверку гипотез о свойствах экономических показателей
• эмпирический вывод экономических законов
• построение экономических моделей
• закономерности и взаимозависимости в экономике методами математической статистики

Вопрос 10. M(X) и D(X) – это …

• линейные функции
• числовые характеристики генеральной совокупности (числа)
• функции
• нелинейные функции

Вопрос 11. Для разных выборок, взятых из одной и той же генеральной совокупности, выборочные средние …

• и дисперсии будут одинаковы
• будут одинаковы, а дисперсии будут различны
• будут различны, а дисперсии будут одинаковы
• и дисперсии будут различны

Вопрос 12. Стандартными уровнями значимости являются …% и …% уровни

Вопрос 13. Если наблюдаемое значение критерия больше критического значения, то гипотеза …

• H1 отвергается
• H1 принимается
• H0 отвергается
• H0 принимается

Вопрос 14. Величина var(y) – это дисперсия значений … переменной

• наблюдаемых зависимой
• наблюдаемых независимой
• расчетных зависимой
• расчетных независимой

Вопрос 15. Коэффициентом детерминации R2 характеризуют долю вариации переменной … с помощью уравнения регрессии

• зависимой, объясненную
• зависимой, необъясненную
• независимой, объясненную
• независимой, необъясненную

Вопрос 16. Пространственные данные – это данные, полученные от … моменту (ам) времени

• одного объекта, относящиеся к разным
• разных однотипных объектов, относящихся к разным
• разных однотипных объектов, относящихся к одному и тому же
• одного объекта, относящиеся к одному

Вопрос 17. При идентификации модели производится … модели

• проверка адекватности
• оценка параметров
• статистический анализ и оценка параметров
• статистический анализ

Вопрос 18. Геометрически, математическое ожидание случайной величины – это … распределения

• центр
• мера рассеяния относительно центра
• мера отклонения симметричного от нормального
• мера отклонения от симметричного

Вопрос 19. Если случайные величины Х, У независимы, то …

Вопрос 20. Если случайные величины независимы, то теоретическая ковариация …

• положительная
• отрицательная
• равна нулю
• не равна нулю

Вопрос 21. Некоррелированность случайных величин означает …

• отсутствие линейной связи между ними
• отсутствие любой связи между ними
• их независимость
• отсутствие нелинейной связи между ними

Вопрос 22. Коэффициенты регрессии (а, b) в выборочном уравнении регрессии определяются методом (ами) …

• наименьших квадратов
• взвешенных наименьших квадратов
• моментов
• градиентными

Вопрос 23. Коэффициент регрессии b показывает …

• на сколько единиц в среднем изменяется переменная y при увеличении независимой переменной x на единицу
• прогнозируемое значение зависимой переменной при x = 0
• прогнозируемое значение зависимой переменной при x > 0
• прогнозируемое значение зависимой переменной при x 0
• прогнозируемое значение зависимой переменной при x
• О заказе и гарантиях
• Оформление работ
• Вопросы и ответы

Пример нахождения коэффициента детерминации

Коэффициент детерминации рассчитывается для оценки качества подбора уравнения регрессии. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Значение коэффициента детерминации R 2 = 1 означает функциональную зависимость между переменными.

Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции r_xy: R 2 = r_xy 2 .
2 «>Рассчитать свое значение
Например, значение R 2 = 0.83, означает, что в 83% случаев изменения х приводят к изменению y . Другими словами, точность подбора уравнения регрессии — высокая.

В общем случае, коэффициент детерминации находится по формуле: 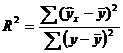или
В этой формуле указаны дисперсии: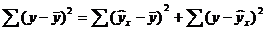
,
где ∑(y- y ) 2 — общая сумма квадратов отклонений;
— сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
— остаточная сумма квадратов отклонений.

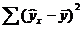
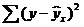
В случае нелинейной регрессии коэффициент детерминации рассчитывается через этот калькулятор. При множественной регрессии, коэффициент детемрминации можно найти через сервис Множественная регрессия

Пример . Дано:

• доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и в покупку валюты, в общей сумме среднедушевого денежного дохода, % (Y)
• среднемесячная начисленная заработная плата, тыс. руб. (X)

Следует выполнить: 1. построить поле корреляции и сформировать гипотезу о возможной форме и направлении связи; 2. рассчитать параметры уравнений линейной и A1; 3. выполнить расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят B2 % от их среднего уровня; 4. оценить тесноту связи с помощью показателей корреляции и детерминации, проанализировать их значения; 5. Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом; 6. Оценить с помощью средней ошибки аппроксимации качество уравнений; 7. Оценить надежность уравнений в целом через F-критерий Фишера для уровня значимости а = 0,05. По значениям характеристик, рассчитанных в пп. 5,6 и данном пункте, выберете лучшее уравнение регрессии и дайте его обоснование.

• Решение онлайн
• Видео решение

Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии

Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции.
R 2 = 0.91 2 = 0.83, т.е. в 83% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
15.1	255	228.01	65025	3850.5	505.26	527451.17	62630.22	420.25
17	261	289	68121	4437	549.38	518772.07	83161.41	345.96
12	293	144	85849	3516	433.28	473699.53	19678.51	556.96
10	310	100	96100	3100	386.84	450587.75	5904.58	655.36
74	1425	5476	2030625	105450	1872.88	196906.67	200600	1474.56
83	1985	6889	3940225	164755	2081.86	1007497.33	9381.6	2246.76
85	2549	7225	6497401	216665	2128.3	2457813.93	176990.6	2440.36
81	2012	6561	4048144	162972	2035.42	1062428.38	548.49	2061.16
22	1562	484	2439844	34364	665.47	337260.88	803758.38	184.96
10	386	100	148996	3860	386.84	354332.48	0.71	655.36
4	383	16	146689	1532	247.52	357913.03	18353.53	998.56
14.1	354.1	198.81	125386.81	4992.81	482.04	393327.58	16368.87	462.25
427.2	11775.1	27710.82	19692405.81	709494.31	11775.1	8137990.81	1397376.9	12502.5

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим

Анализ точности определения оценок коэффициентов регрессии

S _a = 3.3432
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-557.64;913.38)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (6.95>1.812).

Статистическая значимость коэффициента регрессии b не подтверждается (0.96 Fkp, то коэффициент детерминации статистически значим

Коэффициент детерминации

Коэффициент детерминации (R2)— это доля объяснённой дисперсии отклонений зависимой переменной от её среднего значения. Зависимая переменная объясняется (прогнозируется) с помощью функции от объясняющих переменных, в частном случае является квадратом коэффициента корреляции между зависимой переменной и её прогнозными значениями с помощью объясняющих переменных. Тогда можно сказать, что R2 показывает, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных.

Формула для вычисления коэффициента детерминации:

где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии -среднее арифметическое зависимой переменной.

Содержание

· 1 Проблемы и общие свойства R2

o 1.1 Интерпретация

o 1.2 Общие свойства для МНК регрессии

o 1.3 Общие свойства для МНК регрессии со свободным членом (единичным фактором)

o 1.4 Мнимая регрессия

· 2 Решение проблем или модификации R2

o 2.1 R2-скорректированный (adjusted)

o 2.2 R2-распространённый (extended)

o 2.3 R2-истинный (несмещённый)

· 3 Прочие используемые критерии

[править]Проблемы и общие свойства R2

[править]Интерпретация

Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):

Количественная мера тесноты связи

Качественная характеристика силы связи

Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

[править]Общие свойства для МНК регрессии

Линейная множественная регрессия методом наименьших квадратов (МНК) — наиболее распространённый случай использования коэффициента детерминации R2.

Линейная множественная МНК регрессия имеет следующие общие свойства [1]:

1. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.

2. С увеличением количества объясняющих переменных увеличивается R2.

[править]Общие свойства для МНК регрессии со свободным членом (единичным фактором)

Для случая наличия в такой регрессии свободного члена коэффициент детерминации обладает следующими свойствами: [2]

1. принимает значения из интервала (отрезка) [0;1].

2. в случае парной линейной регрессионной МНК модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть R2 = r2. А в случае множественной МНК регрессии R2 = r(y;f)2. Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.[3]

3. R2 можно разложить по вкладу каждого фактора в значение R2, причём вклад каждого такого фактора будет положительным. Используется разложение: , где r0j — выборочный коэффициент корреляции зависимой и соответствующей второму индексу объясняющей переменной.

4. R2 связан с проверкой гипотезы о том, что истинные значения коэффициентов при объясняющих переменных равны нулю, в сравнении с альтернативной гипотезой, что не все истинные значения коэффициентов равны нулю. Тогда случайная величина имеет F-распределение с (k-1) и (n-k) степенями свободы.

[править]Мнимая регрессия

Значения R2, , также могут быть манипулированы, с помощью включения фиктивных факторов. Например, если два показателя имеют возрастающую динамику, то их коэффициент корреляции (который входит в факторное разложение) будет достаточно высок. Поэтому логическая и смысловая адекватность модели имеют первостепенную важность. Только качество модели может быль проверено или сопоставлено с использованием R2 и его модификаций.

[править]Решение проблем или модификации R2

[править]R2-скорректированный (adjusted)

Для того, чтобы исследователи не увеличивали R2 с помощью добавления посторонних факторов, R2 заменяется на скорректированный , который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество объясняющих переменных, включая свободный член.>

[править]R2-распространённый (extended)

В случае отсутствия в линейной множественной МНК регрессии свободного члена все четыре вышеперечисленных свойства могут нарушаться для конкретной реализации. Поэтому регрессию со свободным членом и без него нельзя сравнивать по критерию R2. Эта проблема решается с помощью построения распространённого коэффициента детерминации , который будет совпадать с исходным для случая МНК регрессии со свободным членом, и для которого будут продолжать выполняться четыре свойства перечисленые выше. Суть этого метода заключается рассмотрении проекции единичного вектора на плоскость объясняющих переменных [2].
Для случая регрессии без свободного члена:
,
где X — матрица nxk значений факторов, P(X) = X * (X‘ * X) − 1 * X‘ — проектор на плоскость X, , где in — единичный вектор nx1.

с условием небольшой модификации, также подходит для сравнения между собой регрессий построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

[править]R2-истинный (несмещённый)

[править]Прочие используемые критерии

AIC — информационный критерий Акаике — применяется исключительно для сравнения между моделями. Чем меньше значение тем лучше. Часто используется в виде сравнения моделей временных рядов с разным количеством лагов.
. Даёт меньший штраф за включение лишних лагов в модель, чем BIC.
BIC — информационный критерий Шварца — используется и интерпретируется аналогично AIC.
. Даёт больший штраф за включение лишних лагов в модель, чем BIC (см. формулу). [1]

[править]См. также

§ Дисперсия случайной величины

§ Метод группового учета аргументов

[править]Примечания

1. ↑ 1 2 , , Эконометрика. Начальный курс.. — 6,7,8-е изд., доп. и перераб.. — Москва: Дело, 2004. — Т. «». — 576 с. — ISBN -X

2. ↑ 1 2 Распространение коэффициента детерминации на общий случай линейной регрессии, оцениваемой с помощью различных версий метода наименьших квадратов (рус., англ.) //ЦЕМИ РАН Экономика и математические методы. — Москва: ЦЕМИ РАН, 2002. — В. 3. — Т. 38. — С. 107-120.

3. ↑ , Прикладная статистика. Основы эконометрики (в 2-х т.). — . — Москва: Юнити-Дана (проект TASIS), 2001. — Т. «1,2». — 1088 с. — ISBN -8

4. ↑ Выбор регрессии максимизирующий несмещённую оценку коэффициента детерминации (рус., англ.) // Прикладная эконометрика. — Москва: Маркет ДС, 2008. — В. 4. — Т. 12. — С. 71-83.

📽️ Видео