Содержание:
Волновые параметры длинной линии:
Полученные в предыдущей лекции уравнения передачи длинной линии (23.8) описывают комплексные амплитуды напряжения
Тогда для мгновенных значений напряжений и токов в линии получаем:
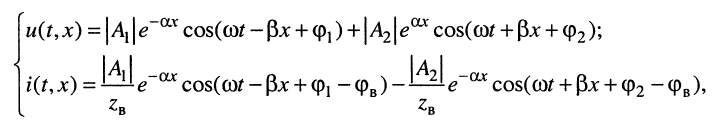
где 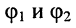
Решения (24.1) подтверждают, что напряжения и токи в длинной.линии являются функциями как времени 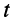
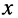
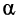
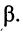
напряжений и токов, которые назовём падающими волнами напряжения и тока (смысл такого названия будет ясен из дальнейшего):
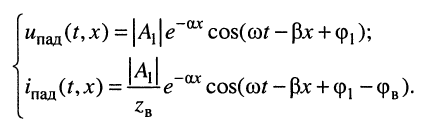
Из этих выражений следует:
- при любом фиксированном
т. е. в любом сечении линии, и напряжение
и ток
являются гармоническими колебаниями;
- амплитуды колебаний убывают по мере удаления от начала к концу линии по экспоненциальному закону
- в любом сечении линии отношение амплитуды напряжения
к амплитуде тока
равно модулю волнового сопротивления
а разность фаз между ними равна аргументу
волнового сопротивления линии;
- колебание напряжения
или тока
в сечении
отстаёт по фазе от колебания и
или
поскольку коэффициент фазы является величиной положительной:
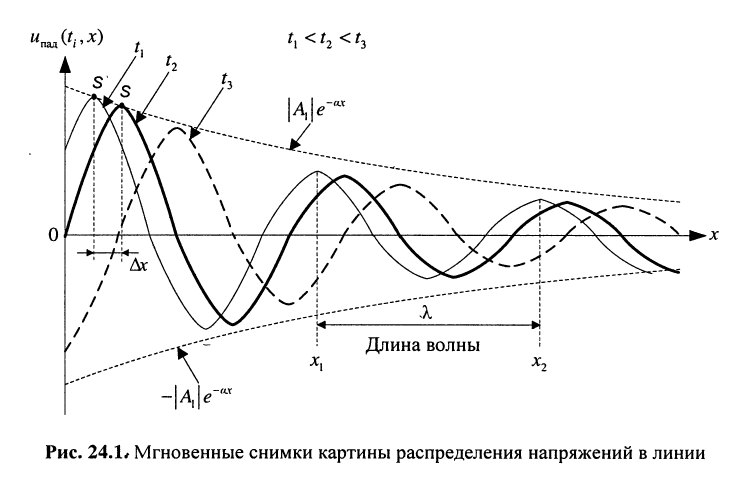
Сказанное демонстрируется на рис. 24.1, где представлено графическое распределение мгновенных значений напряжений 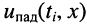
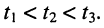
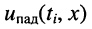
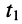
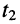
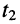
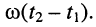
Определение:
Совокупность волн напряжения 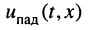
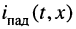
Найдём длину 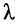
Под длиной волны понимают расстояние между смежными сечениями линии, фаза колебаний волны на которых отличается на 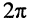
откуда имеем равенство
из которого получаем формулу для вычисления длины волны:
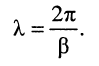
Определение:
Скоростью распространения, или фазовой скоростью, называют скорость 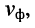
Нуль напряжения достигается в точках, где функция косинуса равна нулю, поэтому условие состояния равной фазы можно записать в виде равенства:
при этом аргумент имеет значения:
Продифференцировав обе части полученного равенства по переменной t, найдём скорость распространения нуля
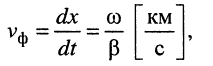
т. е. скорость распространения состояния равной фазы.
Фазовая скорость показывает, какое расстояние 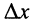
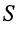
Рассмотрим, чему будет равен коэффициент фазы в наиболее характерной для практики области частот, когда 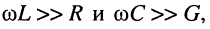
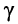
Разложение в ряды полученных в правой части биномиальных сомножителей и удержание в разложениях лишь по два слагаемых даёт:
Раскрывая скобки и пренебрегая в произведении величиной второго порядка малости, получаем приближённое выражение для коэффициента распространения:
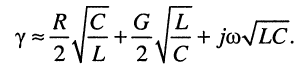
В линиях с хорошим диэлектриком проводимость чрезвычайно мала, поэтому второе вещественное слагаемое в выражении (24.5) оказывается очень малым по сравнению с первым, что позволяет записать формулы для коэффициентов затухания и фазы с хорошей степенью приближения:
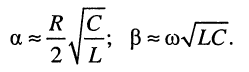
Тогда в указанной выше области частот фазовая скорость (24.4) согласно (24.6) оказывается равной
Подставляя сюда формулы значений первичных параметров длинной линии L и С (табл. 23.1), получаем:
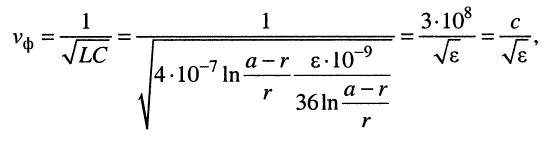
где с — скорость света.
Из (24.7) ясно, что для воздушных линий 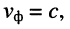
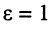
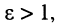
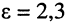
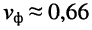
Интересно, что в области низких частот значение фазовой скорости убывает с уменьшением частоты. Это объясняется меньшим проявлением скин-эффекта: волна больше проникает в проводник, и колеблющиеся частицы внутри проводника возбуждают вторичные волны. Поскольку частицы обладают некоторой инерцией, образуемые ими вторичные волны запаздывают по фазе относительно вынуждающей колебания волны, поэтому происходит запаздывание фазы результирующей волны и, как следствие, уменьшение фазовой скорости.
Обратимся теперь ко вторым слагаемым уравнений (24.1), которые назовём отражёнными волнами напряжения и тока:
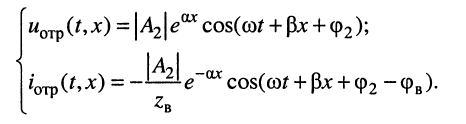
Проведя анализ этих слагаемых подобно тому, как это сделано для падающих волн, нетрудно убедиться, что они описывают затухающую волну такого же характера, как и падающая, но распространяющуюся в обратном направлении: от конца к началу линии.
Определение:
Волна напряжения 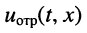
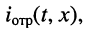
- Соотношения между комплексными амплитудами падающих и отражённых волн
- Волновое сопротивление
- Коэффициент отражения
- Уравнения передачи согласованно нагруженной длинной линии
- Постоянная передачи и частотные характеристики длинной линии
- Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии
- Входное сопротивление длинной линии
- Определение параметров линии методом холостого хода и короткого замыкания
- Ультразвук. Основы теории распространения ультразвуковых волн
- Основные параметры ультразвука
- Разновидности ультразвуковых волн
- Визуализация ультразвуковых волн
- Интенсивность и мощность ультразвука
- Затухание ультразвука
- Отражение ультразвука от границы раздела сред
- Интерференция и дифракция ультразвуковых волн
- Излучатели ультразвука
- Характеристики излучателя ультразвука
- Звуковое поле излучателя
- Применение ультразвука
- Коэффициент затухания в волновом уравнение
- 🔥 Видео
Видео:4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Соотношения между комплексными амплитудами падающих и отражённых волн
Из анализа, выполненного в разд. 24.1, следует:
- фазовая скорость отражённой волны совпадает с точностью до знака с фазовой скоростью падающей волны
- амплитуда напряжения (тока) отражённой волны максимальна в конце амплитуда напряжения (тока) падающей волны минимальна в конце линии;
- напряжение
(ток) в любой точке длинной линии
х является суммой напряжений (токов) падающей и отражённой волн:
Переходя к комплексным амплитудам напряжений и токов падающей и отражённой волн, входящих в уравнения передачи длинной линии (23.8), последние суммы для любого сечения линии можно записать в виде:
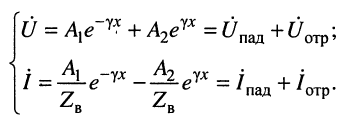
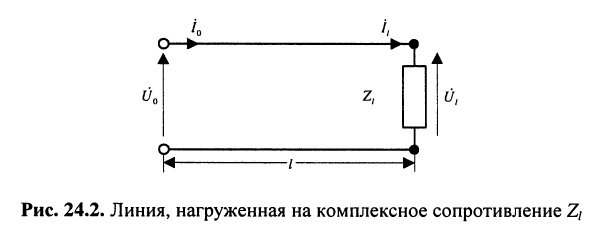
Практический интерес представляют соотношения между комплексными амплитудами падающих и отражённых волн в линии, имеющей длину 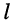
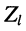
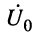
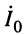
Волновое сопротивление
Прежде всего отметим, что при любом jc, т. е. в любой точке линии согласно (24.9) справедливы равенства:
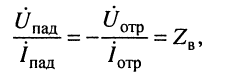
которое говорит о том, что в любом сечении линии .отношение комплексных амплитуд напряжения и тока падающей (отражённой) волны равно волновому сопротивлению линии
Свойства волнового сопротивления можно определить из выражений (24.10) и (23.6):
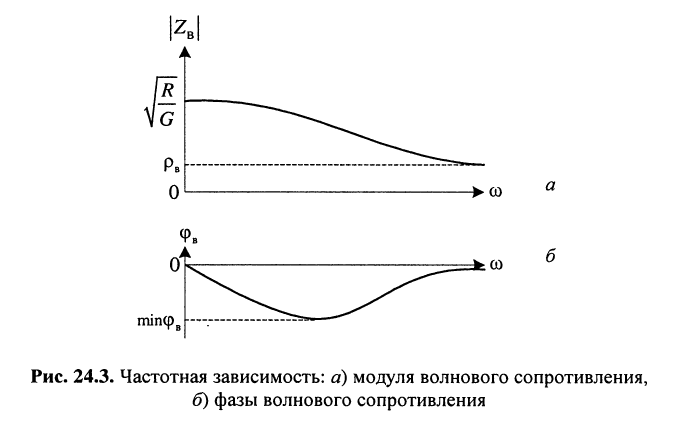
из которых следует:
модуль волнового сопротивления 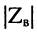
фаза (угол) 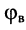
на частоте 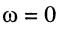
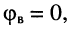
при стремлении частоты к бесконечности 
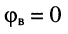
модуль волнового сопротивления 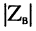
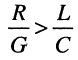
изменение фазы от нулевого значения при 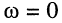

Коэффициент отражения
Что касается соотношения между комплексными амплитудами напряжения (тока) падающей и отражённой волн, то оно оказывается различным в различных сечениях линии. Установить эти соотношения можно из системы (23.8), положив 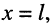
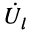
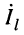
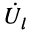
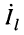
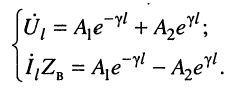
Из системы (24.11) согласно правилу Крамера получаем значения постоянных 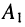
Подстановка найденных значений 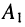
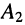
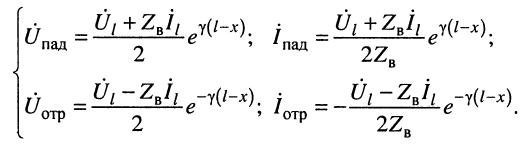
Система уравнений (24.12) позволяет записать отношение комплексных амплитуд напряжений и токов отражённой и падающей волн в сечении линии, расположенном на расстоянии 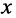
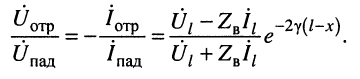
Но при выбранных направлениях отсчётов (рис. 24.2) напряжения 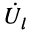
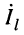
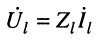
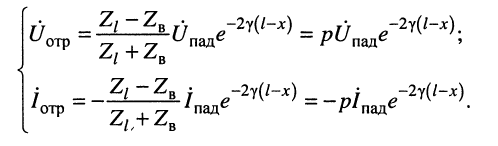
Определение:
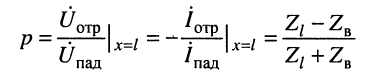
комплексной амплитуды напряжения отражённой волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.
Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:
1. Коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии 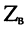
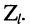
2. Коэффициент отражения по току отличается от коэффициента отражения по напряжению только знаком.
3. При 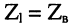
4. Отношение амплитуд отражённой и падающей волн (см. (24.14) и (24.15))
убывает с удалением от конца линии к её началу
5. В режиме короткого замыкания, когда 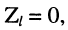
р = 1. Это означает, что напряжения отражённой и падающей волн в конце линии находятся в противофазе:
а результирующее напряжение равно нулю
при этом токи падающей и отражённой волн оказываются в фазе
и результирующий ток равен удвоенному току падающей волны
6. В режиме холостого хода, когда 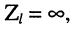
и результирующее напряжение равно удвоенному напряжению падающей волны
а ток равен нулю
Уравнения передачи согласованно нагруженной длинной линии
Ранее (см. разд. 23.3) были получены уравнения передачи длинной линии (23.8), которые представляют собой общее решение телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения же большинства практических задач достаточно знать соотношения лишь между напряжениями и токами на внешних зажимах линии и вовсе не интересоваться законом распределения напряжений и токов по длине линии. Иначе говоря, на практике вполне достаточно рассматривать линию как согласованно нагруженный четырёхполюсник, полностью описываемый соответствующими уравнениями передачи.
Поставим задачу найти уравнения передачи согласованно нагруженной линии, которые связывают комплексные амплитуды напряжений и токов на её внешних зажимах.
Воспользуемся уравнениями (24.12) для комплексных амплитуд напряжений и токов падающей и отражённой волн и подставим их в систему (24.9):
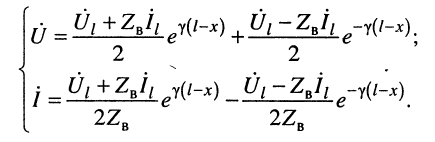
Если в систему (24.9) подставить выражения (24.14), получим
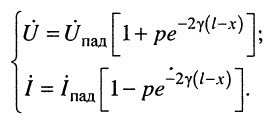
Системы (24.16) и (24.17) представляют собой системы уравнений передачи длинной линии. Обычно комплексные амплитуды напряжения и тока на входных зажимах линии (х = 0) обозначают через 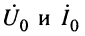
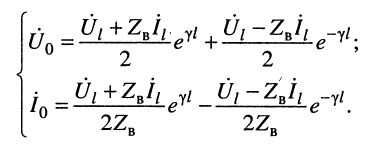
В большинстве случаев уравнения (24.8) записывают в более компактном виде:
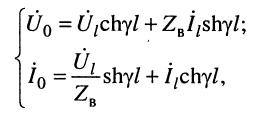
где
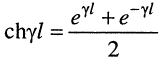
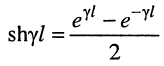
Для режима согласованной нагрузки, когда 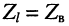
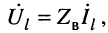
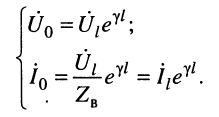
Именно в такой режим и стремятся поставить линию связи, поскольку отражённые волны вызывают ряд нежелательных явлений, о чём речь пойдёт далее.
Постоянная передачи и частотные характеристики длинной линии
Постоянная передачи длинной линии:
Определение
Безразмерная комплексная величина, равная произведению коэффициента распространения 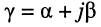
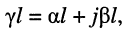
называется постоянной передачи линии.
Вещественная часть постоянной передачи 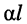
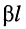
Постоянная передачи и входящие в неё параметры характеризуют линию как таковую и не зависят от свойств генератора и нагрузки, между которыми линия может быть включена.
Поскольку режим согласованной нагрузки для линии является типовым, найдём указанные ранее параметры только для этого режима.
В таком случае постоянную передачи можно получить, прологарифмировав уравнения (24.20):
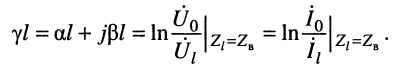
Подставляя отношения комплексных амплитуд
под знак логарифма, получаем:
на основании чего можно записать два равноправных выражения для коэффициента распространения
собственное затухание линии
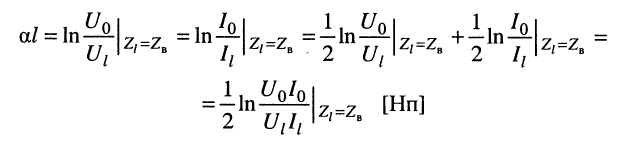
и её собственную фазу
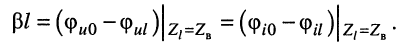
Из выражений (24.23) и (24.24) следует, что для согласованно нагруженной линии:
собственное затухание линии 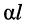
собственная фаза линии равна разности начальных фаз колебаний напряжений (токов) на входе и выходе.
Собственное затухание линии часто оценивается в децибелах:
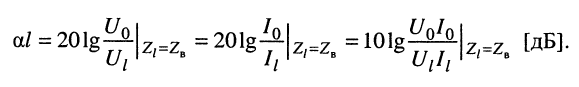
В этом случае нетрудно переформулировать зависимость собственного затухания, выраженного в децибелах, через десятичные логарифмы отношений амплитуд напряжений (токов) или полных мощностей.
Пример 24.1.
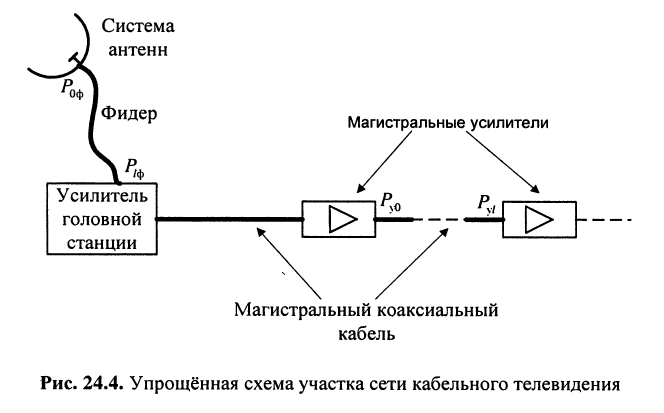
Оценим потери мощности телевизионного сигнала при распространении его в фидере’ от системы антенн до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на отрезках магистральной линии между магистральными усилителями (рис. 24.4).
Решение. Затухание фидера зависит от его конструкции, длины 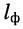
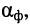
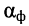
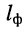
а отношение мощности сигнала на выходе фидера 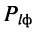
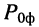
т. е. потери мощности в фидере невелики.
Фидер — линия для передачи электрических колебаний высокой частоты от радиопередатчика к антенне и от антенны к радиоприёмнику.
В то же время типовой магистральный коаксиальный кабель QR 540 JCA имеет полосу пропускания 5—1000 МГц и коэффициент затухания 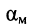
Расстояние 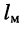
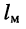
Последнее означает, что полная мощность на входе последующего усилителя 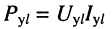
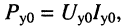
Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии
Исходя из уравнений передачи согласованно нагруженной линии (24.20) запишем её комплексную частотную характеристику через постоянную передачи линии:
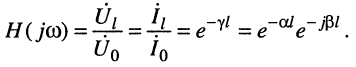
Отсюда нетрудно получить постоянную передачи через КЧХ линии:
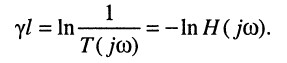
Амплитудно-частотная и фазочастотная характеристики определяются из (24.26):
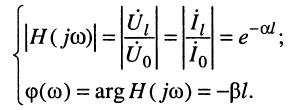
Для несогласованной нагруженной линии КЧХ можно найти из её уравнений передачи (24.18), подставив в них равенства:
где 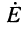
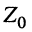
Входное сопротивление длинной линии
Определение:
Входным сопротивлением линии 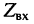
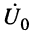
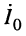
Формулу входного сопротивления для линии с произвольной нагрузкой можно получить из уравнений (24.17), если положить расстояние 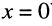
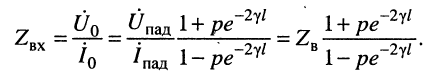
Анализ формулы (24.29) показывает:
при согласованной нагрузке входное сопротивление равно волновому, поскольку в данном случае 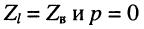
если постоянная передачи линии стремится к бесконечности 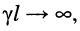
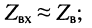
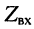
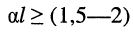
в режиме КЗ 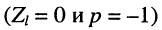
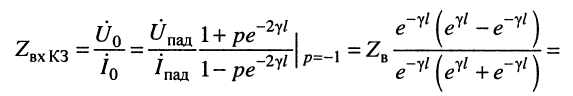
в режиме XX 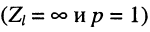
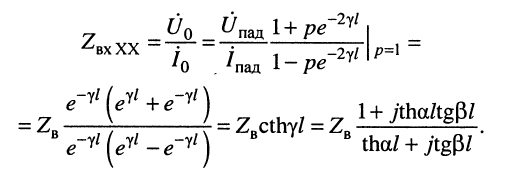
волновое сопротивление линии представляет собой предел, к которому стремится входное сопротивление при безграничном увеличении длины линии:
Этот факт объясняется тем, что при большом затухании линии значительная часть мощности, подводимой к её входу, рассеивается в самой линии и лишь небольшой остаток мощности поступает в нагрузку (см. пример 24.1). По этой причине энергетические соотношения на входе линии пренебрежимо мало зависят от энергетических соотношений на её выходе и, в частности, от сопротивления нагрузки линии.
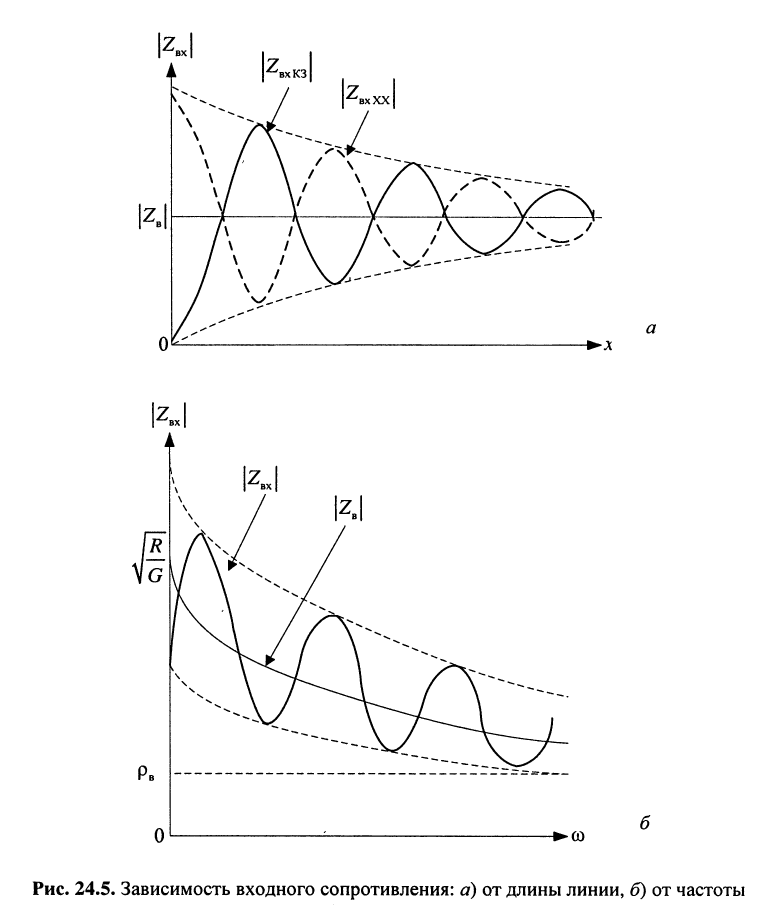
С увеличением длины линии увеличивается и её затухание, а потому уменьшается амплитуда отражённой волны на входе линии, что, в свою очередь, приводит к уменьшению отклонения входного сопротивления линии от её волнового сопротивления как по модулю, так и по фазе. В пределе входное сопротивление линии стремится к волновому сопротивлению. На рис. 24.5, а показаны зависимости модулей входных сопротивлений в режимах XX и КЗ. Колебательный характер волнового сопротивления при несогласованной нагрузке объясняется наличием падающих и отражённых волн.
Входное сопротивление зависит не только от длины линии, но и от частоты (рис. 24.5, б). С ростом частоты увеличиваются как собственное затухание 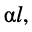
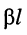
Допустимые отклонения входного сопротивления линии от её волнового сопротивления строго нормированы, и при эксплуатации длинных линий необходимо придерживаться указываемых для линии обычно весьма жёстких норм.
Определение параметров линии методом холостого хода и короткого замыкания
Определение первичных и вторичных параметров линии наиболее просто осуществлять с помощью измерений входного сопротивления линии при двух граничных сопротивлениях нагрузки: холостом ходе и коротком замыкании.
Из уравнений (24.19) в режимах 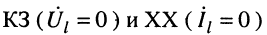
Совместное решение этих уравнений позволяет найти значения волновых параметров линии: волнового сопротивления и постоянной передачи.
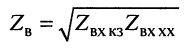
равно среднему геометрическому из входных сопротивлений короткозамкнутой и разомкнутой линии. Это выражение можно рассматривать как ещё одно определение волнового сопротивления длинной линии.
Гиперболический тангенс постоянной передачи
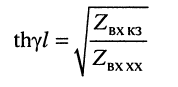
равен среднему геометрическому из сопротивления 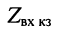
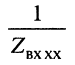
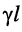
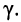
Логарифмируя обе части последнего равенства, получаем постоянную передачи:
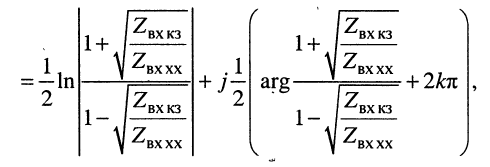
откуда легко находятся коэффициенты затухания и фазы:
Коэффициент 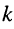
Во всех формулах необходимо брать только арифметические корни.
Зная волновые параметры линии, нетрудно вычислить её первичные параметры путём приравнивания вещественных и мнимых частей равенств:
Метод холостого хода и короткого замыкания целесообразно применять в том случае, когда затухание линии не превышает
1 Нп (8,69 дБ), что характерно для большинства длинных линий.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Колебания в линиях без потерь
- ЭДС и напряжение в электрической цепи
- Закон Ома для участка цепи
- Электрическое сопротивление
- Частотные методы анализа и расчёта электрических цепей
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Ультразвук. Основы теории распространения ультразвуковых волн
Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Основные параметры ультразвука
Основными параметрами волны являются длина волны и период. Число циклов совершенных за одну секунду называется частотой и измеряется в Герцах (Гц). Время, требуемое чтобы совершить полный цикл, называется периодом и измеряется в секундах. Взаимосвязь между частотой и периодом волны приведено в формуле:

Скорость звука в идеальном упругом материале при заданной температуре и давлении является постоянной. Связь между скоростью ультразвука и длиной волны следующая:

В твердых веществах для продольных волн скорость звука [1]

- где cl – скорость звука для продольных волн, м/c,
- E – модуль упругости, Па,
- μ – коэффициент Пуассона,
- ρ – плотность, кг/м 3
Для поперечных волн она определяется по формуле

- где ct – скорость звука для поперечных волн, м/с,
- G – модуль сдвига, Па
Дисперсия звука — зависимость фазовой скорости монохроматических звуковых волн от их частоты. Дисперсия скорости звука может быть обусловлена как физическими свойствами среды, так и присутствием в ней посторонних включений и наличием границ тела, в котором звуковая волна распространяется.
Видео:Численное решение волнового уравнения (2)Скачать

Разновидности ультразвуковых волн
Большинство методов ультразвукового исследования использует либо продольные, либо поперечные волны. Также существуют и другие формы распространения ультразвука, включая поверхностные волны и волны Лэмба.
Продольные ультразвуковые волны – волны, направление распространения которых совпадает с направлением смещений и скоростей частиц среды.
Поперечные ультразвуковые волны – волны, распространяющиеся в направлении, перпендикулярном к плоскости, в которой лежат направления смещений и скоростей частиц тела, то же, что и сдвиговые волны [2].
Поверхностные (Рэлеевские) ультразвуковые волны имеют эллиптическое движение частиц и распространяются по поверхности материала. Их скорость приблизительно составляет 90% скорости распространения поперечной волны, а их проникновение вглубь материала равно примерно одной длине волны [3].
Волна Лэмба — упругая волна, распространяющиеся в твёрдой пластине (слое) со свободными границами, в которой колебательное смещение частиц происходит как в направлении распространения волны, так и перпендикулярно плоскости пластины. Лэмба волны представляют собой один из типов нормальных волн в упругом волноводе – в пластине со свободными границами. Т.к. эти волны должны удовлетворять не только уравнениям теории упругости, но и граничным условиям на поверхности пластины, картина движения в них и их свойства более сложны, чем у волн в неограниченных твёрдых телах.
Видео:Численное решение волнового уравненияСкачать

Визуализация ультразвуковых волн
Видео:4.1 Однородные волновые уравнения ГельмгольцаСкачать

Интенсивность и мощность ультразвука
Интенсивность звука (сила звука) — средняя по времени энергия, переносимая звуковой волной через единичную площадку, перпендикулярную к направлению распространения волны, в единицу времени. Для периодического звука усреднение производится либо за промежуток времени большой по сравнению с периодом, либо за целое число периодов [2]. Интенсивность ультразвука – величина, которая выражает мощность акустического поля в точке [6].
Для плоской синусоидальной бегущей волны интенсивность ультразвука I определяется по формуле

- где р — амплитуда звукового давления, Па
- v — амплитуда колебательной скорости частиц, м/c
- ρ — плотность среды, кг/м 3
- с — скорость звука, м/c
В сферической бегущей волне интенсивность ультразвука обратно пропорциональна квадрату расстояния от источника. В стоячей волне I = 0, т. е. потока звуковой энергии в среднем нет. Интенсивность ультразвука в гармонической плоской бегущей волне равна плотности энергии звуковой волны, умноженной на скорость звука. Поток звуковой энергии характеризуют так называемым вектором Умова — вектором плотности потока энергии звуковой волны, который можно представить как произведение интенсивности ультразвука на вектор волновой нормали, т. е. единичный вектор, перпендикулярный фронту волны. Если звуковое поле представляет собой суперпозицию гармонических волн различной частоты, то для вектора средней плотности потока звуковой энергии имеет место аддитивность составляющих.
Для излучателей, создающих плоскую волну, говорят об интенсивности излучения, понимая под этим удельную мощность излучателя, т. е. излучаемую мощность звука, отнесённую к единице площади излучающей поверхности.
Интенсивность звука измеряется в системе единиц СИ в Вт/м 2 . В ультразвуковой технике интервал изменения интенсивности ультразвука очень велик — от пороговых значений
10 -12 Вт/м 2 до сотен кВт/м 2 в фокусе ультразвуковых концентраторов.
Мощность звука — энергия, передаваемая звуковой волной через рассматриваемую поверхность в единицу времени. Различают мгновенное значение мощности ультразвука и среднее за период или за длительное время. Наибольший интерес представляет среднее значение мощности ультразвука, отнесённое к единице площади, т. н. средняя удельная мощность звука, или интенсивность звука [2].
Таблица 1 — Свойства некоторых распространенных материалов [6]
| Материал | Плотность, кг/м 3 | Скорость продольной волны, м/c | Скорость поперечной волны, м/c | Акустический импеданс, 10 3 кг/(м 2 *с) |
| Акрил | 1180 | 2670 | — | 3,15 |
| Воздух | 0,1 | 330 | — | 0,00033 |
| Алюминий | 2700 | 6320 | 3130 | 17,064 |
| Латунь | 8100 | 4430 | 2120 | 35,883 |
| Медь | 8900 | 4700 | 2260 | 41,830 |
| Стекло | 3600 | 4260 | 2560 | 15,336 |
| Никель | 8800 | 5630 | 2960 | 49,544 |
| Полиамид (нейлон) | 1100 | 2620 | 1080 | 2,882 |
| Сталь (низколегированный сплав) | 7850 | 5940 | 3250 | 46,629 |
| Титан | 4540 | 6230 | 3180 | 26,284 |
| Вольфрам | 19100 | 5460 | 2620 | 104,286 |
| Вода (293К) | 1000 | 1480 | — | 1,480 |
Видео:Задача Коши для волнового уравнения (Часть 1)Скачать

Затухание ультразвука
Одной из основных характеристик ультразвука является его затухание. Затухание ультразвука – это уменьшение амплитуды и, следовательно, интенсивности звуковой волны по мере ее распространения. Затухание ультразвука происходит из-за ряда причин. Основными из них являются:
- убывание амплитуды волны с расстоянием от источника, обусловленное формой и волновыми размерами источника;
- рассеяние ультразвука на неоднородностях среды, в результате чего уменьшается поток энергии в первоначальном направлении распространения;
- поглощение ультразвука, т.е. необратимый переход энергии звуковой волны в другие формы, в частности в тепло.
Первая из этих причин связана с тем, что по мере распространения волны от точечного или сферического источника энергия, излучаемая источником, распределяется на все увеличивающуюся поверхность волнового фронта и соответственно уменьшается поток энергии через единицу поверхности, т.е. интенсивность звука. Для сферической волны, волновая поверхность которой растёт с расстоянием r от источника как r 2 , амплитуда волны убывает пропорционально r -1 , а для цилиндрической волны — пропорционально r -1/2 .
Рассеяние ультразвука происходит из-за резкого изменения свойств среды – её плотности и модулей упругости — на границе неоднородностей, размеры которых сравнимы с длиной волны. В газах это могут быть, например, жидкие капли, в водной среде — пузырьки воздуха, в твёрдых телах — различные инородные включения или отдельные кристаллиты в поликристаллах и т. п. Особый интерес представляет рассеяние на хаотически распределённых в пространстве неоднородностях.
Поглощение ультразвука может быть обусловлено различными механизмами. Большую роль играет вязкость и теплопроводность среды, взаимодействие волны с различными молекулярными процессами вещества, с тепловыми колебаниями кристаллической решётки и др.
3атухание звука, обусловленное рассеянием и поглощением, описывается экспоненциальным законом убывания амплитуды с расстоянием, т. е. амплитуда пропорциональна e -δr , а интенсивность – e -2δr в отличие от степенного закона убывания амплитуды при расхождении волны, где δ – коэффициент затухания звука [2].
Коэффициент затухания выражают либо в децибелах на метр (дБ/м), либо в неперах на метр (Нп/м).
Для плоской волны коэффициент затухания по амплитуде с расстоянием определяется по формуле [4]

- где α – коэффициент затухания с расстоянием, 1/м,
- L – расстояние, м,
- p(0), p(L) – амплитуда звукового давления в исходной точке и на расстояние L, Па
Коэффициент затухания от времени определяется [5]

- где β – коэффициент затухания от времени, 1/с,
- T – время, с,
- p(0), p(T) – амплитуда звукового давления в начале и через время T соответственно, Па
Для измерения коэффициента также используют единицу дБ/м, в этом случае

Децибел (дБ) – логарифмическая единица измерения отношения энергий или мощностей в акустике [2].

- где A1 – амплитуда первого сигнала,
- A2 – амплитуда второго сигнала
Тогда связь между единицами измерения (дБ/м) и (1/м) будет:

Коэффициент затухания выражается либо в децибелах на метр (дб/м), либо в неперах на метр (Нп/м) или что тоже самое м -1 . Затухание в 1 Нп/м означает, что на расстоянии 1м амплитуда волны уменьшается в e раз (e =2,71 — основание натуральных логарифмов или число непера).
Видео:4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

Отражение ультразвука от границы раздела сред
При падении звуковой волны на границу раздела сред, часть энергии будет отражаться в первую среду, а остальная энергия будет проходить во вторую среду. Соотношение между отраженной энергией и энергией, проходящей во вторую среду, определяется волновыми сопротивлениями первой и второй среды. При отсутствии дисперсии скорости звука волновое сопротивление не зависит от формы волны и выражается формулой:

- где Z – волновое сопротивление, кг/(м 2 с),
- ρ – плотность, кг/м 3 ,
- с – скорость звука, м/с
Коэффициенты отражения и прохождения будут определяться следующим образом

- где R – коэффициент отражения звукового давления [1],
- Z1 – волновое сопротивление первого вещества, в котором распространяется звуковая волна, кг/(м 2 с),
- Z2 – волновое сопротивление второго вещества, в которую проходит звуковая волна, кг/(м 2 с)

- где D – коэффициент прохождения звукового давления
Стоит отметить также, что если вторая среда акустически более «мягкая», т.е. Z1>Z2, то при отражении фаза волны изменяется на 180˚ [1].
Коэффициент пропускания энергии τ из одной среды в другую определяется отношением интенсивности волны, проходящей во вторую среду, к интенсивности падающей волны

Видео:Микропроект. Решение волнового уравнения.Скачать

Интерференция и дифракция ультразвуковых волн
Интерференция звука — неравномерность пространственного распределения амплитуды результирующей звуковой волны в зависимости от соотношения между фазами волн, складывающихся в той или иной точке пространства. При сложении гармонических волн одинаковой частоты результирующее пространственное распределение амплитуд образует не зависящую от времени интерференционную картину, которая соответствует изменению разности фаз составляющих волн при переходе от точки к точке. Для двух интерферирующих волн эта картина на плоскости имеет вид чередующихся полос усиления и ослабления амплитуды величины, характеризующей звуковое поле (например, звукового давления). Для двух плоских волн полосы прямолинейны с амплитудой, меняющейся поперёк полос соответственно изменению разности фаз. Важный частный случай интерференции — сложение плоской волны с её отражением от плоской границы; при этом образуется стоячая волна с плоскостями узлов и пучностей, расположенными параллельно границе.
Дифракция звука — отклонение поведения звука от законов геометрической акустики, обусловленное волновой природой звука. Результат дифракции звука — расхождение ультразвуковых пучков при удалении от излучателя или после прохождения через отверстие в экране, загибание звуковых волн в область тени позади препятствий, больших по сравнению с длиной волны, отсутствие тени позади препятствий, малых по сравнению с длиной волны, и т. п. Звуковые поля, создаваемые дифракцией исходной волны на препятствиях, помещённых в среду, на неоднородностях самой среды, а также на неровностях и неоднородностях границ среды, называются рассеянными полями. Для объектов, на которых происходит дифракция звука, больших по сравнению с длиной волны λ, степень отклонений от геометрической картины зависит от значения волнового параметра

- где D — поперечник объекта (например, поперечник ультразвукового излучателя или препятствия),
- r — расстояние точки наблюдения от этого объекта
Видео:Вывод волнового уравненияСкачать

Излучатели ультразвука
Излучатели ультразвука — устройства, применяемые для возбуждения ультразвуковых колебаний и волн в газообразных, жидких и твердых средах. Излучатели ультразвука преобразуют в энергию звукового поля энергию какого-либо другого вида.
Наибольшее распространение в качестве излучателей ультразвука получили электроакустические преобразователи. В подавляющем большинстве излучателей ультразвука этого типа, а именно в пьезоэлектрических преобразователях, магнитострикционных преобразователях, электродинамических излучателях, электромагнитных и электростатических излучателях, электрическая энергия преобразуется в энергию колебаний какого-либо твердого тела (излучающей пластинки, стержня, диафрагмы и т.п.), которое и излучает в окружающую среду акустические волны. Все перечисленные преобразователи, как правило, линейны, и, следовательно, колебания излучающей системы воспроизводят по форме возбуждающий электрический сигнал; лишь при очень больших амплитудах колебаний вблизи верхней границы динамического диапазона излучателя ультразвука могут возникнуть нелинейные искажения.
В преобразователях, предназначенных для излучения монохроматической волны, используется явление резонанса: они работают на одном из собственных колебаний механической колебательной системы, на частоту которого настраивается генератор электрических колебаний, возбуждающий преобразователь. Электроакустические преобразователи, не обладающие твердотельной излучающей системой, применяются в качестве излучателей ультразвука сравнительно редко; к ним относятся, например, излучатели ультразвука, основанные на электрическом разряде в жидкости или на электрострикции жидкости [2].
Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Характеристики излучателя ультразвука
К основным характеристикам излучателей ультразвука относятся их частотный спектр, излучаемая мощность звука, направленность излучения. В случае моночастотного излучения основными характеристиками являются рабочая частота излучателя ультразвука и его частотная полоса, границы которой определяются падением излучаемой мощности в два раза по сравнению с её значением на частоте максимального излучения. Для резонансных электроакустических преобразователей рабочей частотой является собственная частота f0 преобразователя, а ширина полосы Δf определяется его добротностью Q.

Излучатели ультразвука (электроакустические преобразователи) характеризуются чувствительностью, электроакустическим коэффициентом полезного действия и собственным электрическим импедансом.
Чувствительность излучателя ультразвука — отношение звукового давления в максимуме характеристики направленности на определённом расстоянии от излучателя (чаще всего на расстоянии 1 м) к электрическому напряжению на нём или к протекающему в нём току. Эта характеристика применяется к излучателям ультразвука, используемым в системах звуковой сигнализации, в гидролокации и в других подобных устройствах. Для излучателей технологического назначения, применяемых, например, при ультразвуковых очистке, коагуляции, воздействии на химические процессы, основной характеристикой является мощность. Наряду с общей излучаемой мощностью, оцениваемой в Вт, излучатели ультразвука характеризуют удельной мощностью, т. е. средней мощностью, приходящейся на единицу площади излучающей поверхности, или усреднённой интенсивностью излучения в ближнем поле, оцениваемой в Вт/м 2 .
Эффективность электроакустических преобразователей, излучающих акустическую энергию в озвучиваемую среду, характеризуют величиной их электроакустического коэффициента полезного действия, представляющего собой отношение излучаемой акустической мощности к затрачиваемой электрической. В акустоэлектронике для оценки эффективности излучателей ультразвука используют так называемый коэффициент электрических потерь, равный отношению (в дБ) электрической мощности к акустической. Эффективность ультразвуковых инструментов, используемых при ультразвуковой сварке, механической обработке и тому подобное, характеризуют так называемым коэффициентом эффективности, представляющим собой отношение квадрата амплитуды колебательного смещения на рабочем конце концентратора к электрической мощности, потребляемой преобразователем. Иногда для характеристики преобразования энергии в излучателях ультразвука используют эффективный коэффициент электромеханической связи.
Видео:Вывод волнового уравненияСкачать

Звуковое поле излучателя
Звуковое поле преобразователя делят на две зоны: ближнюю зону и дальнюю зону. Ближняя зона это район прямо перед преобразователем, где амплитуда эха проходит через серию максимумов и минимумов. Ближняя зона заканчивается на последнем максимуме, который располагается на расстоянии N от преобразователя. Известно, что расположение последнего максимума является естественным фокусом преобразователя. Дальняя зона это район находящийся за N, где давление звукового поля постепенно уменьшается до нуля [1].
Положение последнего максимума N на акустической оси в свою очередь зависит от диаметра и длины волны и для дискового круглого излучателя выражается формулой

- где N – длина ближней зоны, м,
- D – диаметр излучателя, м,
- λ – длина волны, м
Однако поскольку D обычно значительно больше λ, уравнение можно упростить и привести к виду

Характеристики звукового поля определяются конструкцией ультразвукового преобразователя. Следовательно, от его формы зависит распространение звука в исследуемой области и чувствительность датчика.
Видео:Получение уравнения плоской бегущей волны.Скачать

Применение ультразвука
Многообразные применения ультразвука, при которых используются различные его особенности, можно условно разбить на три направления. Первое связано с получением информации посредством ультразвуковых волн, второе — с активным воздействием на вещество и третье — с обработкой и передачей сигналов (направления перечислены в порядке их исторического становления). При каждом конкретном применении используется ультразвук определённого частотного диапазона.
Получение информации с помощью ультразвуковых методов. Ультразвуковые методы широко используются в научных исследованиях для изучения свойств и строения веществ, для выяснения проходящих в них процессов на макро- и микроуровнях. Эти методы основаны главным образом на зависимости скорости распространения и затухания акустических волн от свойств веществ и от процессов, в них происходящих.
Воздействие ультразвука на вещество. Активное воздействие ультразвука на вещество, приводящее к необратимым изменениям в нём, или воздействие ультразвука на физические процессы, влияющее на их ход, обусловлено в большинстве случаев нелинейными эффектами в звуковом поле. Такое воздействие широко используется в промышленной технологии; при этом решаемые с помощью ультразвуковой технологии задачи, а также и сам механизм ультразвукового воздействия различны для разных сред.
Обработка и передача сигналов. Ультразвуковые устройства применяются для преобразования и аналоговой обработки электрических сигналов в различных отраслях радиоэлектроники, например в радиолокации, связи, вычислительной технике, и для управления световыми сигналами в оптике и оптоэлектронике. В устройствах для управления электрическими сигналами используются следующие особенности ультразвука: малая по сравнению с электромагнитными волнами скорость распространения; малое поглощение в кристаллах и соответственно высокая добротность резонаторов [2].
Видео:3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать

Коэффициент затухания в волновом уравнение
4.1. Механические колебания.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания.
4.1.1. Гармонические колебания.
4.1. 1 -1. Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с. Найти время t ₁ , за которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х( t ₁) = А/2 (1)
t ₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону синуса с начальной фазой ϕ ₀ = 0:
x = Asin ( ωt + ϕ ₀) или
x = Asinωt , (2)
где ω = 2 π / T – круговая частота.
С учётом условия (1), запишем (2) в виде:
х( t ₁) = Asin ( ωt ₁); А/2 = Asin ( (2 π / T ) t ₁ ); 1/2 = sin (2 πt ₁/ T ); 2 πt ₁/ T = π /6. Отсюда
t ₁ = T /12.
t₁ = 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
где − I момент инерции диска относительно оси вращения, проходящей через точку подвеса А (см. рис.); x = AO = R − расстояние от точки подвеса до центра тяжести О диска; m − масса диска; g = 9,8 м/с² − ускорение свободного падения.
Момент инерции I ₀ диска относительно оси симметрии диска:
I ₀ = mR ²/2.
По теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
Решение:
r ( t ) = A ( icosωt + jsinωt ) (1)
A = 0,5 м
ω = 5 с⁻¹
v − ?
an − ?
Представим (1) в виде:
r ( t ) = iAcosωt + jAsinωt (1*)
Радиус вектор r ( t ) точки: r ( t ) = ix + jy , где x , y − проекции радиус вектора соответственно на оси OX и OY ; i , j − единичные векторы (орты), направленные соответственно по оси OX и OY . Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt ,
отсюда получим два уравнения
x = Acosωt , (*)
y = Asinωt . (**)
Возведём их в квадрат
x ² = A ² cos ² ωt ,
y ² = A ² sin ² ωt .
Сложим эти уравнения
x ² + y ² = A ² cos ² ωt + A ² sin ² ωt или x ² + y ² = A ²( cos ² ωt + sin ² ωt ). Отсюда, т.к. cos ² ωt + sin ² ωt = 1, получим уравнение траектории движения точки
x ² + y ² = A ². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5 м с центром в начале координат (см. рис.).
Найдём проекции скорости v x и vy . Для этого продифференцируем x и y из (*) и (**) по времени t :
vx = xt ʹ = ( Acosωt ) t ʹ = — Aωsinωt ;
vy = yt ʹ = ( Asinωt ) t ʹ = Aωcosωt .
Тогда квадрат скорости
v ² = vx ² + vy ² или v ² = (- Aωsinωt )² + ( Aωcosωt )² или v ² = A ² ω ²( sin ² ωt + cos ² ωt ) или v ² = A ² ω ². Отсюда модуль скорости v :
v = Aω . (3)
v = 0,5·5 = 2,5 м/с².
Модуль нормального ускорения an : an = v ²/ R или, с учётом (3) и R = A , получим an = A ² ω ²/ A или
an = Aω ².
an = 0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5 м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω ² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1. Амплитуда затухающих колебаний уменьшилась в n = 100 за 15 с. Чему равен коэффициент затухания β ?
Решение:
t = 15 c
n = 100
A = A ₀/ n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t :
A = A ₀ e — β t , (1)
где A ₀ – начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A ₀/ n = A ₀ e — β t ; 1/ n = e — β t ; e β t = n ; βt = ln ( n ) отсюда
β = ln ( n )/ t .
β = ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти логарифмический декремент затухания тонкого стержня, подвешенного за один из его концов, если за промежуток времени t = 5 мин его полная механическая энергия уменьшилась в n = 4 · 10 ² раз. Длина стержня L = 50 см.
Решение:
t = 5 мин = 300 с
n = 400
L = 0,5 м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT , (1)
где β – коэффициент затухания, T − период колебаний стержня.
1. Найдём коэффициент затухания β .
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω – частота затухающих колебаний; ω ₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E ₀ e -2 βt ,
где E ₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е ₀/ Е = Е ₀/( E ₀ e -2 βt ) = 1 /( e -2 βt ) = e 2 βt .
Получили n = e 2 βt . Прологарифмируем это равенство Ln ( n ) = 2 βt . Отсюда
β = Ln ( n )/(2 t ). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент β 2 по (3).
β = Ln (400)/(2 · 300) = 0,009986, отсюда
β ² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
4.1.2-3. Логарифмический декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02. Определите: время, за которое амплитуда колебаний тела уменьшится в 20 раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.
Решение:
ν = 50 Гц
λ = 0,02
n = 20
t − ?
N − ?
1. Пусть β – коэффициент затухания; T = 1/ ν – период, ν – частота колебаний. Логарифмический декремент затухания λ :
λ = βT или λ = β / ν , отсюда
β = λν . (1)
Амплитуда А затухающих колебаний
A = A ₀· e — βt ,
где A ₀ − начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A ₀/ n :
A ₀/ n = A ₀· e — βt ,
отсюда e βt = n и, после логарифмирования, βt = Ln ( n ), отсюда
t = ( Ln ( n ) )/ β и, с учётом (1),
t = ( Ln ( n ) )/( λν ). (2)
2. Число колебаний N за время t :
N = t / T = tν = ( и, с учётом (2), ) = ν ( Ln ( n ) )/( λν ) или
N = ( Ln ( n ) )/ λ . (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln (20) )/(0,02·50) ≈ 3 с.
N = ( Ln (20) )/0,02 ≈ 150.
Ответ: t = ( Ln ( n ) )/( λν ) ≈ 3 с; N = ( Ln ( n ) )/ λ ≈ 150.
4.1.2-4. Составьте дифференциальное уравнение гармонических свободных затухающих крутильных колебаний механической системы.
Решение:
Пусть система (например, тонкий однородный диск, подвешенный в горизонтальном положении к упругой нити) совершает крутильные колебания относительно закреплённой оси Z (ось нити). Пусть на диск действует упругая сила, проекция момента которой на ось Z равна
Mz = — kϕ , (1)
где k − постоянная, ϕ − угол поворота из положения равновесия. Знак “минус” указывает на то, что при отклонении системы на угол ϕ , момент упругой силы возвращает систему к положению равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы сопротивления Mc , действующий на диск, пропорционален угловой скорости ϕ ʹ:
M c = — ηϕ ʹ, (2)
где η − постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕ ʹʹ = Mz + M c , (3)
где I – момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕ ʹʹ = — kϕ — ηϕ ʹ, отсюда
ϕ ʹʹ + ( η / I ) ϕ ʹ + ( k / I ) ϕ = 0.
Применив обозначения 2 β = η / I , ω ₀² = k / I , перепишем последнее уравнение:
ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания механической системы.
Ответ: ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
4.1.2-5. Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω − период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1. Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ = π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:
где f₀ = F ₀/ m , m − масса осциллятора , β − коэффициент затухания, ω₀ − собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной амплитуде вынуждающей силы F ₀ (и, следовательно, постоянной f ₀) из (*) при двух разных частотах ω₁ и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
4.2. Электрические колебания.
4.2-1. Небольшая магнитная стрелка совершает малые колебания вокруг оси, перпендикулярной направлению внешнего магнитного поля. При изменении индукции этого поля период колебаний стрелки уменьшился в η = 5 раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний пренебрежимо мало.
Решение:
T ₁/ T ₂ = η = 5
B ₂/ B ₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного поля
М = [ B · P m ], где P m − вектор магнитного момента стрелки.
Модуль момента сил
М = B · P m · sinϕ , где ϕ – угол между векторами B и P m .
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ . Тогда
М = B · P m · ϕ .
При повороте стрелки на угол ϕ возникает момент сил М , стремящийся вернуть стрелку в положение равновесия, т.е. М = — B · P m · ϕ . Если J – момент инерции стрелки относительно оси вращения, то основное уравнение динамики вращательного движения примет вид
Jϕ ’’ = M или Jϕ ’’ = — B · P m · ϕ отсюда
ϕ ’’ + ( B · P m / J ) · ϕ = 0. (1)
Если ω – циклическая частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ ’’ + ω ² ϕ = 0, получим
ω ² = B · P m / J , отсюда
ω = √( B · P m / J ).
Тогда период T колебаний
T = 2 π / ω или
T = 2 π √( J /( B · P m ) ). (2)
На основе (2) для разных B ₁ и B ₂ получим соответствующие T ₁ и T ₂
T ₁ = 2 π √( J /( B ₁ · P m ) )
T ₂ = 2 π √( J /( B ₂ · P m ) ).
Отсюда
T ₁/ T ₂ = √( B ₂/ B ₁) и отсюда
B ₂/ B ₁ = ( T ₁/ T ₂)² = η ² = 25. Итак
B ₂/ B ₁ = η ² = 25.
Ответ: индукция магнитного поля увеличится в η ² = 25 раз.
4.2-2. Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4 cos (1000 t ), где все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4 cos (1000 t ). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos ( ωt ). (2)
Из (1) и (2) имеем
Im = 0,4 А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: X L = ωL .
По закону Ома
Im = Um / X L , отсюда
Um = X L · Im или
Um = ωL · Im .
Um = 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.
4.2-3. Электрический колебательный контур состоял из последовательно соединенных катушки с индуктивностью L = 0,8 Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов было равно R = 2000 Ом. После того, как часть витков в катушке замкнулась накоротко, индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре возросла в k = 3 раза, а коэффициент затухания этих колебаний не изменился. Определить емкость конденсатора .
Решение:
L = 0,8 Гн
R = 2000 Ом
L ₂ = L / n
n = 7
ω ₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R /(2 L ).
ω и ω ₂ − начальная и конечная частоты собственных колебаний в контуре, где
ω = √( 1/( LC ) — β ² ) = √( 1/( LC ) — R ²/(4 L ²) );
ω ₂ = √( 1/( L ₂ C ) — β ² ) = √( n /( LC ) — R ²/(4 L ²) ).
Возведём в квадрат равенство ω ₂ = kω , получим ω ₂² = k ² ω ² или
n /( LC ) — R ²/(4 L ²) = k ²( 1/( LC ) — R ²/(4 L ²) ), отсюда
C = 4 L ( k ² — n )/( R ²( k ² — 1) ).
C = 4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4. Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0 мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе в момент времени t = 0 ( Um − максимальное напряжение ):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
4.3. Упругие волны. Акустика.
4.3-1. По шнуру слева направо бежит со скоростью v незатухающая гармоническая волна. При этом поперечное смещение точки О шнура изменяется по закону y = Acos ( ωt ). Как зависит от времени смещение точки шнура, находящейся правее точки О на расстоянии x от нее?
Решение:
y = Acos ( ω ( t — x / v ) ).
Ответ: y = Acos ( ω ( t – x / v ) ).
4.3-2. Уравнение плоской звуковой волны имеет вид ξ = 60 cos (1800 t — 5,3 x ). где ξ – в мкм, t – в секундах, х – в метрах .
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx). (2)
Из (1) и (2) следует
A = 60 ·10 ⁻ ⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A / λ = 60 ·10 ⁻ ⁶ · 5,3/(2 · 3,14) = 5,1 ·10 ⁻ ⁵ .
б) Амплитуда колебаний скорости частиц среды
V m = Aω . (*)
Vm = 60 ·10 ⁻ ⁶ · 1800 = 0,11 м/с. = 11 см/с.
Скорость распространения волны
v = ω / k . (3)
Тогда ( см. (*) )
Vm/v = Aω / ( ω / k ) = A k .
Vm/v = A k .
Vm/v = 60 ·10 ⁻ ⁶ · 5,3 = 3,2 ·10 ⁻ ⁴ .
в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ ξ/ ∂ x = ( Acos(ωt – kx) )x ʹ = — Aksin (ωt – kx).
Ответ: a) A/λ = 5,1 ·10 ⁻ ⁵ ;
б) Vm = 0,11 м/с, Vm/v = 3,2 ·10 ⁻ ⁴;
в) ( ∂ ξ/ ∂ x)m = 3,2 ·10 ⁻ ⁴, V m = v · (d ξ/dx)m , где v = 340 м/с – скорость волны .
4.3-3. Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню на простом примере. В озере на воде поплавок. Бросьте в воду камешек, от него во все стороны пойдут волны. Поплавок колеблется на волнах. Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда колебаний скорости частиц среды
Vm = Aω ( A — амплитуда, ω — циклическая частота).
Скорость распространения волны
v = ω / k ( k — волновое число).
A , ω , k определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos ( ωt – kx ).
4.3-4. Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45 кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ = 50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника, амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед косинусом):
A = (A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂ соответственно
A ₁ = ( A ₀ / r ₁ ) · e ⁻ ᵞ r₁ , (**)
A ₂ = ( A ₀ / r ₂ ) · e ⁻ ᵞ r ₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
η = ( r ₂ / r ₁ ) · e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ отсюда η r ₁ / r ₂ = e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ , отсюда, по определению логарифма, имеем
ln ( η r ₁ / r ₂ ) = γ( r ₂ — r ₁ ), отсюда
γ = ln(3 · 5 /10 )/(10 — 5 ) ≈ 0,08 м ⁻ ¹ .
б). Для нахождения скорости смещения частиц среды V найдём частную производную по времени t от (1):
V = ∂ ξ / ∂ t = ( A ₀ / r ) · e ⁻ ᵞ ʳ ·( — ω sin ( ω t — kr ) ).
С учётом ω = 2πν, имеем
V = — ( 2 π ν A ₀ /r ) ·e ⁻ ᵞ ʳ ·sin ( ω t-kr ) .
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
4.3-5. Плоская звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со скоростью 300 мс в воздухе, плотность которого равна 1 , 2 кгм ³ . Определить интенсивность волны.
Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300 мс
ρ = 1,2 кгм³
I − ?
Интенсивность I звуковой волны
I = ρ а² ω ² V /2 и т.к. ω = 2 πν , то
I = ρ а²(2 πν )² V /2.
I = 1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6. Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне. Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l = πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1. Электромагнитная волна с частотой 6 · 10 ¹⁴ Гц распространяется в стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и значение волнового числа?
Решение:
ν = 6 · 10¹⁴ Гц
n = 1,5
c = 3 · 10⁸ м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны в стекле:
V = c / n . (1)
Длина волны в стекле:
λ = V / ν = c /( nν ). (*)
Волновое число k:
k = 2 π / λ или с учётом (*)
k = 2 πnν /с. (2)
Вычисления по (1), (2)
V = 3 · 10⁸/1,5 = 2 · 10⁸ м/с.
k = 2 · 3,14 · 1,5 · 6 · 10¹⁴/(3 · 10⁸) = 1,88 · 10⁷ (1/м).
Ответ: V = 2 · 10⁸ м/с; k = 1,88 · 10⁷ (1/м).
4.4-2. Определить показатель преломления призмы из парафина , если его диэлектрическая проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C / V . (1)
С – скорость света в вакууме.
Скорость света в среде
V = C /√( Ԑμ ). (2)
Из (1) и (2) имеем
n = √( Ԑμ ).
n = √(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________
🔥 Видео
Лекция 2 ВолныСкачать

10. Волновое уравнение на отрезке. Сложные задачиСкачать

Решение волнового уравнения в три руки под запись на камеру 8000fpsСкачать

Решение волнового уравнения в прямоугольникеСкачать

Классические уравнения | волновое уравнение | элементарнейшие случаи двумерных волнСкачать

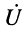
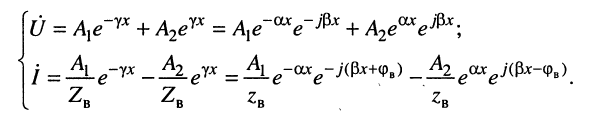
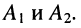
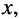 т. е. в любом сечении линии, и напряжение
т. е. в любом сечении линии, и напряжение 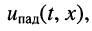 и ток
и ток 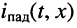 являются гармоническими колебаниями;
являются гармоническими колебаниями;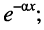
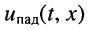 к амплитуде тока
к амплитуде тока 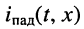 равно модулю волнового сопротивления
равно модулю волнового сопротивления 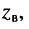 а разность фаз между ними равна аргументу
а разность фаз между ними равна аргументу 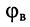 волнового сопротивления линии;
волнового сопротивления линии;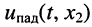 или тока
или тока 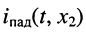 в сечении
в сечении 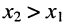 отстаёт по фазе от колебания и
отстаёт по фазе от колебания и 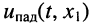 или
или 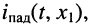 поскольку коэффициент фазы является величиной положительной:
поскольку коэффициент фазы является величиной положительной: 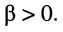
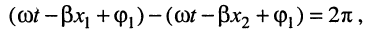
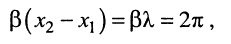
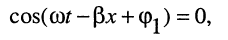
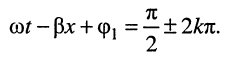
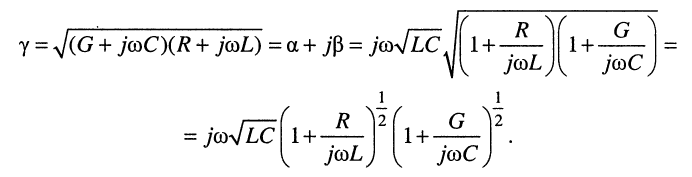
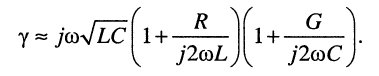
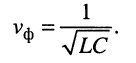
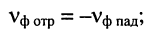
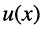 (ток) в любой точке длинной линии
(ток) в любой точке длинной линии 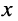 х является суммой напряжений (токов) падающей и отражённой волн:
х является суммой напряжений (токов) падающей и отражённой волн: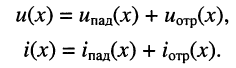
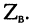
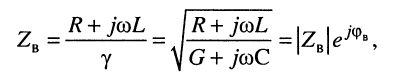
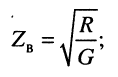
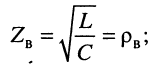
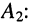
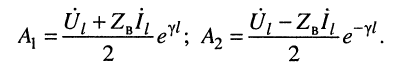
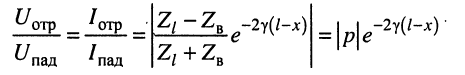
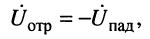
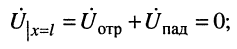
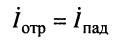
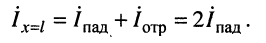
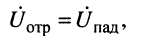
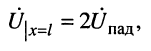
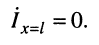
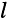
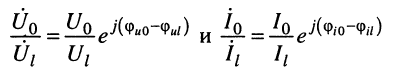
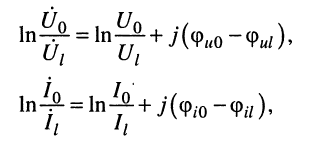
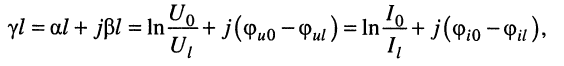
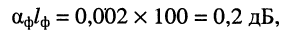
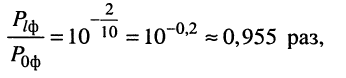
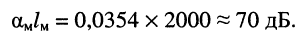
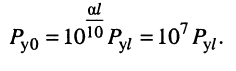
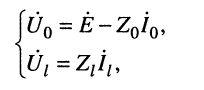
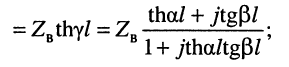
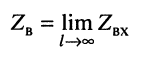
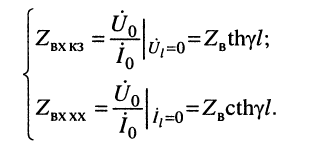
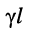
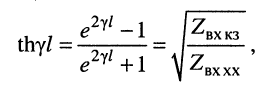
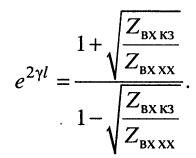
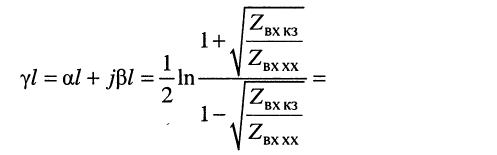
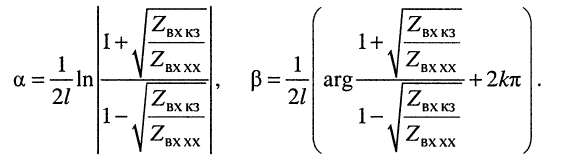
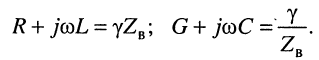


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)



.jpg)