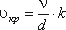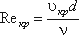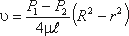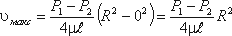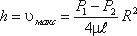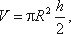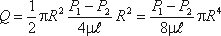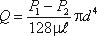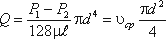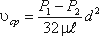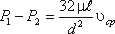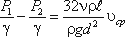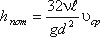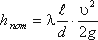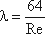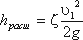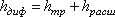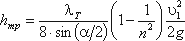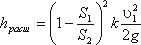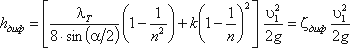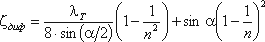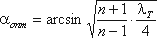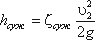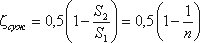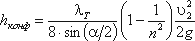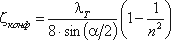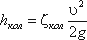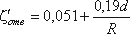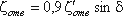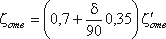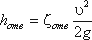Коэффициент трения лямбда в уравнении дарси вейсбаха при турбулентном движении потока зависит от

Видео:Гидравлические сопротивления. Сопротивления трения. Уравнение Дарси-ВейсбахаСкачать

Коэффициент трения лямбда в уравнении дарси вейсбаха при турбулентном движении потока зависит от

Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода — это линейные потери; в других — они сосредоточены на очень коротких участках, длиной которых можно пренебречь, — на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.

Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

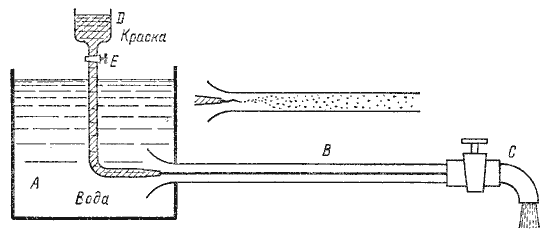
При наблюдении за движением жидкости в трубах и каналах, можно заметить, что в одном случае жидкость сохраняет определенный строй своих частиц, а в других — перемещаются бессистемно. Однако исчерпывающие опыты по этому вопросу были проведены Рейнольдсом в 1883 г. На рис. 4.1 изображена установка, аналогичная той, на которой Рейнольдс производил свои опыты.

Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.

Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ _кр.

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

Как показывает опыт, для труб круглого сечения Re_кр примерно равно 2300.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.

В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.

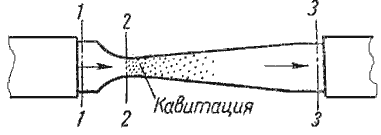
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.

При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.

Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.

При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.

Таким образом, кавитация — это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.

Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.

Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.

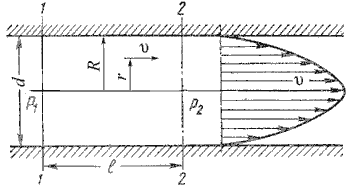
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью — квадратичную параболу (рис.4.3).

Уравнение, связывающее переменные υ и r, имеет следующий вид:

где P1 и P2 — давления соответственно в сечениях 1 и 2.

У стенок трубы величина r = R, , значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной

Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.

Максимальная скорость дает высоту параболоида

Как известно из геометрии, объем параболоида высотой h и площадью ρR 2 равен

а в нашем случае

Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид

Расход в трубе можно выразить через среднюю скорость:

Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).

Потеря давления в трубопроводе будет равна

Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

Так как левая часть полученного равенства равна потерям напора h_пот в трубе постоянного диаметра, то окончательно это равенство примет вид:

Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:

где λ — коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re 2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

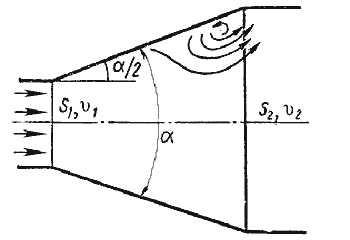
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

где k — коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

откуда коэффициент сопротивления диффузора можно выразить формулой

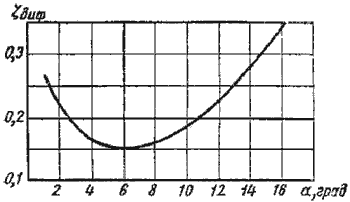
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рис.4.11).

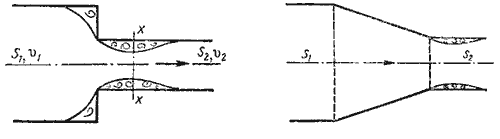
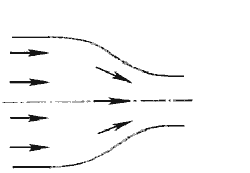
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).

Полная потеря напора определится по формуле ;

где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

в которой n = S₁/S₂ — степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

где коэффициент сопротивления конфузора определяется по формуле

в которой n = S₁/S₂ — степень сужения.

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).

5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

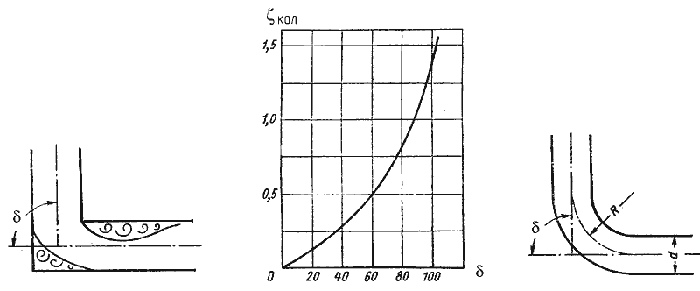
где ζ_кол — коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рис.4.16).

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 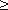1 при турбулентном течении можно воспользоваться эмпирической формулой:

Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Вывод формулы Дарси-Вейсбаха

Преобразуем полученное нами на прошлой лекции выражение закона Гагена-Пуазейля (6.7), выразив расход Q через произведение средней скорости и площади поперечного сечения

для удобства использования зависимости (7.1) при решении практических задач преобразуем ее следующим образом: коэффициент трения на единицу длины (коэффициент Дарси), получим окончательно потери по длине

учитывая, что , получим

Обозначая через гидравлический коэффициент трения на единицу длины (коэффициент Дарси), получим окончательно, что потери по длине

Зависимость (7.2) называется формулой Дарси-Вейсбаха и следует отметить, что для ламинарного режима течения гидравлический коэффициент трения получен теоретическим путем.

Видео:Коэффициент тренияСкачать

Турбулентный режим течения. Пульсация скорости

Турбулентный режим течения является более сложным для исследования, чем ламинарный, вследствие интенсивного перемешивания жидкости, пульсации скоростей и давлений. В настоящее время модель турбулентного потока представляют состоящей из трех зон (рис.7.1):

Вязкого подслоя 1, переходной области 2 и области развитого течения или ядра потока 3.

Вязкий подслой 1 располагается в непосредственной близости от стенок, в нем наблюдаются турбулентные пульсации, но они заглушаются силами вязкости. Поэтому в весьма тонком вязком подслое характер течения обусловливается в основном вязким трением. Средняя толщина вязкого подслоя может быть больше или меньше средней высоты выступов шероховатости стенок.

В переходной области силы вязкости соизмеримы с силами инерции и здесь наблюдается неустойчивый режим течения.

В ядре потока течение имеет четко выраженный турбулентный характер с интенсивным перемешиванием жидкости.

Скорость и давление в любой точке турбулентного потока изменяются во времени, причем беспорядочно, непериодически отклоняясь от некоторого устойчивого среднего положения (рис.7.2). Поэтому мгновенную скорость можно предусматривать в виде двух составляющих: -осредненная по времени и -скорость пульсации, которая может быть как со знаком «+», так и со знаком «-». Тогда в общем случае можно записать

Введение понятия осредненной скорости позволило предложить осредненную модель турбулентного потока, которая нашла широкое применение в инженерной гидравлике. Для такой модели справедливы все результаты и зависимости, полученные раньше. Это относится к уравнениям Бернулли, неразрывности и т.д. Распределение скоростей по сечению турбулентного потока носит более сложный характер, чем при ламинарном. Эпюра скоростей носит логарифмический характер и описывается выражением:

n зависит от Re для гидравлически гладких труб.

— осредненная во времени локальная скорость;

-динамическая скорость, определяемая выражением

где — напряжение турбулентного трения;

-плотность; ?-постоянная Кармана, ?= 0,4; с — константа, определяемая из условия, что максимальная осредненная скорость находится в центре потока, т.е. при . Тогда можно записать

турбулентный скорость поток гидравлика

Эпюра осредненных скоростей при турбулентном режиме течения характеризуется следующими особенностями:

• — скорости на поверхности стенки равны нулю;
• — в пристенном слое на весьма малом расстоянии от стенки скорость изменяется от нуля до значений, мало отличающихся от значений скорости в центре потока;
• — в ядре потока скорости изменяются относительно мало, а поэтому мал и градиент скорости.

В связи с вышеупомянутым, коэффициент кинетической энергии или коэффициент Кориолиса в уравнении Бернулли при турбулентном движении принимаем равным , т.е. распределение скоростей более равномерное.

Видео:Закон БернуллиСкачать

Коэффициент трения для турбулентного течения: что и как найти

В этой статье «Коэффициент трения для турбулентного потока» и коэффициент трения для турбулентного потока, связанные с некоторыми сведениями, будут обсуждаться. Распространенным методом определения коэффициента трения для турбулентного потока является диаграмма Муди.

Коэффициент трения представляет собой физический параметр, который является безразмерным. Турбулентный поток для конкретного поля заданного типа является постоянным. Коэффициент трения для турбулентного потока зависит только от геометрии канала и числа Рейнольдса. Течение называется турбулентным, если число Рейнольдса больше 3500.

Видео:Закон БернуллиСкачать

Чему равен коэффициент трения турбулентного потока?

Максимальной системой жидкости в ядерных установках является работающая с проточным типом турбулентного течения. Сопротивление этого потока подчиняется уравнению Дарси – Вейсбаха.

Трение турбулентного потока – это измерение напряжения сдвига, которое прикладывается к стенке стержня или трубы во время турбулентного течения. Турбулентное течение подчиняется уравнению Дарси – Вейсбаха, которое прямо пропорционально квадрату средней скорости текущей жидкости в определенной области..

Турбулентный поток:-

1. Когда значение Число Рейнольдса более 3500 этот тип течения называется турбулентным течением.
2. Математический анализ турбулентного течения не слишком прост.
3. Скорость турбулентного потока слишком высока.
4. Неравномерное движение возникает в жидкостях, которые текут в движении в турбулентном потоке.
5. Возникает среднее движение, в котором течет боковая жидкость.
6. Турбулентное течение вообще очень распространенный тип течения.
7. профиль скорости Турбулентность потока на определенном участке быстро падает, если он касается стенки трубы или стержня.
8. Профиль скорости турбулентного потока в определенной области явно плоский, если речь идет о центральном сечении стержня или трубы.

Видео:Гидравлика и гидрология (лекция 5)Скачать

Формула коэффициента трения для турбулентного потока:

Уравнение Коулбрука – Уайта определяется как f для коэффициента трения Дарси, функция для числа Рейнольдса как , относительная шероховатость трубы выражается как ε / Dh как для гладких, так и для шероховатых труб.

Формула коэффициента трения для турбулентного потока:

= гидравлический диаметр для заполнения жидкостью круглых трубопроводов

= Внутренний диаметр области, откуда течет турбулентный поток

= Гидравлический радиус для заполнения жидкостью круглых трубопроводов

= Внутренний диаметр области, откуда течет турбулентный поток/4

Уравнение Коулбрука решается численно из-за его неявного характера. В настоящее время W-функцию Ламберта также используют для получения откровенной переформулировки уравнения Коулбрука.

Расширенные формы: —

Дополнительная математическая форма уравнения Коулбрука:

1.7384…. = 2 log (2 * 3.7) = 2 log (7.4)

1.1364…. = 1.7384… = – 2 log (2) = 2 log

(7.4) – 2 log (2) = 2 log (3.7)

9.287 = 18.574/2 = 2.51 * 3.7

Видео:Местные гидравлические сопротивленияСкачать

Как рассчитать коэффициент трения для турбулентного потока?

Процесс расчета коэффициента трения для турбулентного потока приведен ниже.

1. Сначала нам нужно определить значение числа Рейнольдса для турбулентного течения по этой формуле,
2. 
3. На следующем шаге относительная шероховатость должна быть рассчитана по формуле frac, значение которой должно быть меньше 0.01.
4. На последнем шаге используйте формулу Муди для шероховатости с помощью числа Рейнольдса,
5. 

Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Коэффициент трения при турбулентном течении в трубе:

Диапазон коэффициента трения для турбулентного течения в трубе равен

Для гладкой трубы,

Для шероховатой трубы,

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Коэффициент трения при турбулентном течении в гладкой трубе:

Коэффициент трения при турбулентном течении в гладкой трубе можно объяснить с помощью корреляции Блазиуса. Корреляция Блазиуса является простейшей формой определения коэффициента трения Дарси.

Корреляция Блазиуса применима только к турбулентному течению в гладких трубах, но не применима к турбулентному течению в неровных трубах. Допустимо значение 100000 числа Рейнольдса корреляции Блазиуса. В некоторых случаях турбулентное течение в неровных трубах применяется только из-за его простоты.

Математическое уравнение корреляции Блазиуса турбулентного течения в неровных трубах приведено ниже,

После этого уравнение корректируется и выражается как

f является функцией для,

D = диаметр трубы, выраженный в метрах, футах

R = радиус кривой, выраженный в метрах, футах

H = шаг по геликоиду, выраженный в метрах, футах

Re = число Рейнольдса, которое безразмерно

Число Рейнольдса действительно для,

Расширенные формы: —

Дополнительная математическая форма уравнения Коулбрука:

1.7384…. = 2 log (2 * 3.7) = 2 log (7.4)

1.1364…. = 1.7384… = – 2 log (2) = 2 log

(7.4) – 2 log (2) = 2 log (3.7)

9.287 = 18.574/2 = 2.51 * 3.7

Видео:Местные гидравлические сопротивленияСкачать

Коэффициенты трения при турбулентном течении в изогнутых трубах:

Чтобы рассчитать падение давления в змеевике или трубе, необходимо сначала рассчитать коэффициент трения.

Факторы трения для турбулентного потока в изогнутых трубах обсуждаются ниже.

D = внутренний диаметр змеевика или трубы

R = Дарий катушки или спирали трубы

De = номер декана

= переходное число Рейнольдса

= коэффициент трения змеевика или трубы, которые гладкие

= коэффициент трения для шероховатого змеевика или трубы

= Коэффициент трения для гладкого змеевика или трубы

Когда в трубе или змеевике возникает однофазный поток, который имеет изогнутую форму, в змеевике или трубе возникает вторичная картина течения, в это время начинают изменяться коэффициент трения и поведение жидкости.

В результате стабилизации потока жидкости на выходе происходит увеличение числа Рейнольдса в точке входа потока в змеевик или трубу, происходит переход течения от ламинарного к турбулентному.

Математическая форма этого условия приведена ниже,

Для расчета коэффициента трения в трубе или змеевике необходимо число Дина,

После этого мы легко можем определить коэффициент трения для гладкого змеевика или трубы.

Для расчета полностью турбулентных потоков определите коэффициент трения для гладкого змеевика или трубы, используя это уравнение:

Видео:Расчёт простого трубопроводаСкачать

Коэффициент трения диаграммы Муди для турбулентного потока:

В турбулентном течении соотношение между числом Рейнольдса выражается как Re, коэффициент трения выражается как , а относительную шероховатость представляют как это сложно.

Выражение для коэффициента трения диаграммы Муди для турбулентного потока:

Видео:Гидравлика и гидрология (лекция 6)Скачать

Часто задаваемые вопросы: —

Видео:ГГд лекция 10Скачать

Вопрос:- Напишите о Диаграмма коэффициента трения Дарси.

Решение:- Диаграмма коэффициента трения Дарси представляет собой комбинацию четырех физических параметров, таких как коэффициент потери давления, число Рейнольдса, относительная шероховатость змеевика или трубы и соотношение диаметров змеевика или трубы.

Диаграмма коэффициента трения Дарси представляет собой безразмерный физический фактор с помощью уравнения Дарси – Вейсбаха, который можно записать как

Падение давления можно рассчитать как,

Выражение для коэффициента трения Дарси для ламинарного потока:

В турбулентном течении соотношение между числом Рейнольдса выражается как Re, коэффициент трения выражается как , а относительную шероховатость представляют как это сложно.

Выражение для коэффициента трения Дарси для турбулентного потока:

Последние больше сообщений о механических

Об Индрани Банерджи

Привет. Я Индрани Банерджи. Я получил степень бакалавра в области машиностроения. Я человек с энтузиазмом, и я человек, который положительно относится ко всем аспектам жизни. Я люблю читать книги и слушать музыку.

🎦 Видео

Формула ПуазёйляСкачать

Лекция КНИТУ, ауд. A-233, МАХП, 10.25-11.55Скачать

Галилео. Эксперимент. Закон БернуллиСкачать

Местные гидравлические сопротивленияСкачать

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Лабораторная работа «Измерение коэффициента трения скольжения»Скачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать