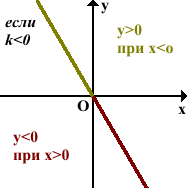Коэффициент прямой пропорциональности называется число k в уравнении вида y kx y

Видео:Функция прямой пропорциональности. 7 класс.Скачать

Коэффициент прямой пропорциональности

Что такое коэффициент прямой пропорциональности? Коэффициент прямой пропорциональности это как?

С прямой пропорциональностью неразрывно связано понятие коэффициент прямой пропорциональности.

Прямая пропорциональность есть функция вида y = kx, см. Прямая пропорциональность определение.

В этой формуле k есть коэффициент прямой пропорциональности.

Рассмотрим примеры коэффициента прямой пропорциональности.

Коэффициент прямой пропорциональности примеры

Пример коэффициента прямой пропорциональности

Здесь коэффициент пропорциональности равен 5. О чем это говорит?

Если мы будем делить значения переменной y на значения переменной x, то всегда будем получать 5, а это и есть наш коэффициент прямой пропорциональности.

Возьмем для примера из области определения три любые значения икс, пусть это будут 2, 30 и 61.

Найдем соответствующие значения y и заполним таблицу для y = 5x

Далее, если мы будем делить значения переменной y на значения переменной x, то всегда будем получать коэффициент пропорциональности 5

То, что все эти частные равны одному и тому же числу 5, и говорит о том, что наша функция y = 5x есть прямая пропорциональность.

Может коэффициент пропорциональности быть целым?

Здесь коэффициент пропорциональности равен 10.

Может коэффициент пропорциональности быть отрицательным?

Здесь коэффициент пропорциональности равен минус 10.

Может коэффициент пропорциональности быть дробным?

Здесь коэффициент пропорциональности равен минус десять целых пять десятых.

Видео:Занятие 1. График линейной функции y=kx+bСкачать

Прямая пропорциональность y = kx и её график

Определение прямой пропорциональности

Если машина движется со скоростью 50 км/ч, пройденное расстояние (в километрах) в зависимости от времени (в часах) s = 50t. Время мы определяем как $tgeq0$. Но механика позволяет нам рассчитать не только будущее положение тела, но и прошлое, подставив в формулу $t lt 0$ и запросто «прокрутив» время назад. Поэтому в общем случае, если движение было и остаётся постоянным, мы получаем:

Можно представить себе не только отрицательное время («поход в прошлое»). Ещё проще ввести отрицательные координаты: направо идём – координата растёт, становится положительной, поворачиваем налево – уменьшается, становится отрицательной.

В задачах, связанных с экономикой, величины также могут уходить в «плюс» и «минус»: покупки/продажи, кредиты/депозиты, доходы/затраты, прибыли/убытки . Часто эти величины изменяются на какую-то постоянную сумму с течением времени.

Если обобщить формулы, описывающие подобные зависимости, то получаем:

$$<left< begin- infty lt x lt + infty — аргумент, quad любое quad действительное quad число \ k = const ≠ 0 quad — параметр, quad константа \ y = kx quad — функцияend right.>$$

Функция такого вида называется прямой пропорциональностью .

Если $k gt 0$, то чем больше x, тем больше y – функция возрастает.

Если $k lt 0$, то чем больше x, тем больше y – функция убывает.

График прямой пропорциональности

Графиком прямой пропорциональности является прямая, проходящая через начало координат.

Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:

Алгоритм построения графика прямой пропорциональности

• Выбрать произвольное значение аргумента $x_*neq 0$
• Вычислить соответствующее значение функции $y_*=kx_*$
• Отметить на координатной плоскости точку $(x_*,y_* )$
• Провести прямую через начало координат (0;0) и точку $(x_*,y_* )$

Эта прямая – график прямой пропорциональности y=kx.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Функция прямая пропорциональность

Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).

Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.

Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).

Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).

Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.

Свойства функции прямой пропорциональности

1) Область определения — множество действительных чисел:

2) Область значений — множество действительных чисел:

3) Нуль функции (y=0) при x=0.

4) При k>0 функция y=kx возрастает, при k 0 график функции проходит через I и III координатные четверти.

Функция принимает положительные значения при положительных значениях аргумента:

Функция принимает отрицательные значения при отрицательных значениях аргумента:

Число k называется угловым коэффициентом прямой y=kx.

k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.

Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.

🎥 Видео

Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Прямая пропорциональность и её график. Алгебра, 7 классСкачать

Алгебра 7 класс. 8 октября. y=kxСкачать

Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Алгебра 7 Линейная функция y=kxСкачать

Алгебра 8 класс (Урок№3 - График функции y=kx)Скачать

Функция y=k/x и ее график. 7 класс.Скачать

Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

7 класс - Алгебра - Определение углового коэффициентаСкачать

Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

Прямая пропорциональность и её графикСкачать

Линейная функция и её график. Алгебра, 7 классСкачать

19 Функция y=kx+b и ее графикСкачать

Линейная функция и ее график. 7 класс.Скачать

Алгебра. Раздел 3. Тема 6. Прямая пропорциональность. Угловой коэффициент прямой y=kx+bСкачать

Построение графика прямой пропорциональностиСкачать

[ОГЭ] На рисунках изображены графики функций вида у = кх + ЬСкачать