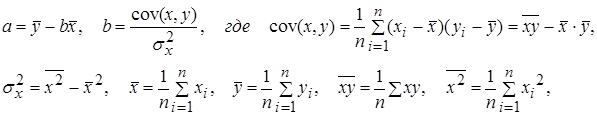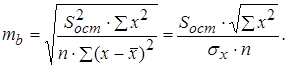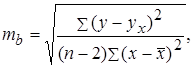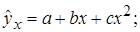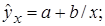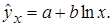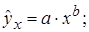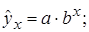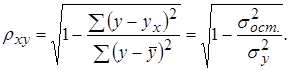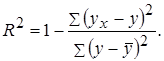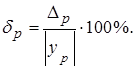Коэффициент корреляции уравнение регрессии шкала чеддока

Для оценки коэффициента линейной корреляции, ее множественного индекса или определения статистических зависимостей количественных показателей от качественных характеристик применяют шкалу Чеддока. Она условна, но широко используется в эконометрике, при построении сложных и многофакторных математических моделей.

Шкала Чеддока, как качественная статистическая характеристика в технико-экономических исследованиях успешно применяется в медицине, экономике, маркетинге и социологии.

На практике в медицине шкала Чеддока чаще всего применяется при расчёте математической статистики и вычисления вероятности событий. Например, при изучении общественного состояния здоровья населения или для углубленного изучения заболеваемости или смертности, в зависимости от возраста и пола, от какого-нибудь заболевания.

Соотношение Чеддока

Базисным научным подходом служит убеждение в том, что ни одно событие не происходит случайно. Математические или статистические закономерности никогда не рассматривают изолированно, обособлено, вне зависимости от влияющих факторов. Любое событие априори считается результатом совместного воздействия множества сил или обстоятельств.

К примеру, на уровень продаж в среднестатистическом магазине влияют:

• площадь торгового помещения;
• уровень освещенности;
• профессионализм персонала и менеджерского состава;
• витринная экспозиция товара;
• дополнительные услуги и сервис;
• покупательная способность населения;
• другие скрытые, неявные и неочевидные факторы.

Еще одним показательным примером служит количество детей в семье.

Оно зависит от:

• продолжительности супружеской жизни;
• религиозных взглядов родителей;
• материального состояния;
• социального статуса;
• репродуктивного здоровья;
• социально-культурных и этнических особенностей.

Шкала Чеддока (коэффициент корреляции определяет зависимости в точном числовом выражении) позволяет с математической достоверностью оценить уровня влияния каждого фактора в отдельности, степень их совместного воздействия на изучаемый показатель или событие.

Соотношение результативных признаков дает возможность переводить любой числовой показатель или количественное значение в качественный параметр. Зависимости шкалы Чеддока-Снедекора приведены в таблице.

Корреляционный коэффициент	0,1-0,3	0,4-0,5	0,6-0,7	0,8-0,9	0,91-0,99
Характеристика связи	Незначительная	Умеренная	Ощутимая	Высокая	Сильная

Математическое соотношение используют для построения одно- или многофакторных линейных моделей при статистическом анализе. Такие модели позволяют определить наличие взаимосвязи рассматриваемых переменных, характеристик, силу влияния или взаимосвязи.

Шкалу Чеддока используют для точного определения ковариационного момента в теории вероятностей, математической статистике, эконометрической сфере. Коэффициент позволяет установить линейную, обратную или квадратную зависимость случайных величин.

Способ обработки больших массивов статистических данных с точным определением тесноты прямой либо обратной связи различных параметров называют корреляционным анализом. Его невозможно выполнять без соотношения Чеддока-Снедекора.

Коэффициенты корреляции зависимости от типов измерительных шкал

В сфере статистического анализа применяют специальные постоянные значения, которые позволяют точно установить взаимосвязь между переменными показателями, измеренными с помощью различных шкал.

Это своеобразное приведение к единому знаменателю. К переменным x и y, вычисляемым в дихотомической шкале, применяют коэффициент ассоциаций Пирсона. Если только одна из непостоянных величин дихотомическая (двоичная) используют точечное двухрядное корреляционное значение.

Виды шкал, в которых применяют соотношение Чеддока-Снедекора:

• X-признаков. Представляет собой способ организации переменных величин в наборах данных, свойств, значений и характеристик для различных статистических наблюдений – метеорологических, медицинских, товарно-сырьевых.
• Интервальная. Отображает разницу между значениями, которые можно рассчитать, но эти соотношения лишены статистического смысла. Интервальная шкала имеет сочетанные свойства номинальной и порядковой математической схемы. Ее используют для вычисления количественного изменения признака или объекта на заданном временном отрезке. Пример – измерение температуры морской воды. Утром она +19°С, к вечеру повышается до +24°С, то есть становится в 1,26 раз больше.
• Ранговая. Используют для классификации признаков, свойств, событий или объектов по принципу «больше-меньше», «теплее-холоднее», «выше-ниже». При измерениях в такой шкале изучаемым объектам присваивают числовое значение в соответствии с выраженностью вычисляемого свойства. Его определяют с помощью соотношения Чеддока-Снедекора.
• Номинальная. Содержит исключительно данные, которые не могут быть упорядочены. С ними не производят арифметические действия. Такую шкалу используют для сортировки массивов статистических данных или объектов по общему признаку. К значениям применяют бисерально-точечный коэффициент корреляции согласно соотношению Чеддока-Снедекора.

При обеих дихотомических переменных используют четырехполевую зависимость в соответствии со шкалой, по которой производились вычисления. Нелинейная взаимосвязь изучаемых объектов лишает смысла введение корреляционной зависимости.

Что такое Шкала Чеддока

Аналитическая группировка количественных данных, качественных характеристик или изучаемых свойств объектов позволяет построить график эмпирической связи между несколькими переменными.

Шкала Чеддока-Снедекора

Шкала Чеддока коэффициент корреляции отображает в числовом выражении. Если он равен или больше 0,7313, влияние фактора либо взаимосвязь свойств считают высокой. Шкалу применяют при вычислении регрессивного (обратного) соотношения показателей.

Геометрический смысл корреляционного коэффициента демонстрирует различие в угле наклона и траектории осей x и y при графическом отображении зависимости. Линейное соотношение указывает на наличие прямой связи переменных или их взаимного влияния.

Оно принимает значение от -1 до +1. Первый показатель означает регрессивную связь, второй – прямую. Шкала Чеддока – это соотношение между случайными факторами или переменными величинами, позволяющее переводить качественные характеристики объектов в относительно точное числовое значение.

В сфере статистического анализа особый смысл имеет расчет множественного корреляционного коэффициента. Он отражает тесноту прямой или линейной связи основной переменной с несколькими влияющими факторами, рассматриваемыми в совокупности.

Множественный коэффициент корреляции, определяемый с помощью шкалы Чеддока-Снедекора, позволяет привести к единому знаменателю результативные признаки и факторные.

Для вычисления остаточной общей суммы квадратов погрешностей или отклонений применяют формулу ∑(y_i-y_x) 2 . Построение регрессионных математических моделей с вычислениями по шкале Чеддока актуально при создании прогностических систем.

В них учитывают только допустимые значения факторных признаков или независимых переменных. Формула Чеддока-Снедекора позволяет предсказать показатель Y при любом отклонении линии Х на графике взаимосвязи.

При прогнозировании среднегодового уровня продаж определенного товара или расчете экономических показателей предприятия за отчетный период можно вычислить соответствие переменных y и x на любом отрезке времени с графическим представлением зависимости.

Правила ввода данных

Применяют группировку значений по общим характеристикам или сортировку статистического массива по одному признаку в номинальной шкале. Правила ввода данных различаются в зависимости от выстраиваемой модели, используемых математической системы, способа обработки.

Для формульных, табличных и графических представлений принципы заполнения информацией используют разные. Правила группировки данных облегчают статистическую обработку.

При сортировании двоичных совокупностей числовые значения классифицируют для учета каждого значения одновременно по обоим интервалам. Их размещают на пересечении соответствующих строк и столбцов.

Правила техники группирования данных для использования в вычислениях по шкале Чеддока-Снедекора:

1. Подобрать подходящее интервальное значение для каждой переменной.
2. Нанести найденные показатели на соответствующие координатные оси графического отображения.
3. Провести от каждой точки соединяющие и направляющие линии для создания рабочей координатной сетки.
4. Поместить каждую пару связанных переменных величин в соответствующую клетку корреляционного поля, присвоив указывающую на свойства отметку.
5. Суммировать значения в строках и столбцах для получения маргинальных вычислений.

В формульные и табличные корреляционные системы вводить значения проще, чем в графические. Нужно всего лишь подставить необходимый коэффициент из приведенной выше шкалы зависимостей.

Показатели корреляции и детерминации

Соотношение Чеддока-Снедекора применяют при анализе массивов статистических данных, изучении практической значимости влияющих факторов или свойств объектов. Его используют построении синтезированных моделей для прогнозирования событийной вероятности.

Шкала Чеддока позволяет дать качественную оценку тесноте связи или взаимного влияния переменных величин. Коэффициент бинарной корреляции имеет особое значение в регрессивных вычислениях степени обратного воздействия результативных признаков на предмет исследования.

В таких расчетах не обойтись без дополнительного показателя. В этом качестве в формулу вводят коэффициент детерминации, который всегда равен квадрату корреляционного показателя. Дополнительный параметр записывают в неизменном виде R 2 .

Показатель детерминации в математических моделях представляет собой долю дисперсии – диапазона возможного разброса цифровых значений случайной переменной относительно вычислительного ожидания.

Коэффициент детерминации получают из известной величины корреляционного показателя, подобранного по шкале Чеддока-Снедекора. Величину рассматривают в качестве универсальной формульной меры зависимостей одной случайной переменной от ряда прочих.

Частный случай показателя детерминации – отношение R 2 линейного, бинарного или множественного корреляционного коэффициента зависимого объекта к факторным величинам.

Такая формула справедлива исключительно для моделей с известным постоянным значением результативного признака. При вычислении двоичной обратной связи (регрессии) значение квадрата корреляционного показателя, называемого индексом детерминации, располагается в диапазоне от -1 до +1.

Для расчета парной регрессии с константой применяют формулу общего вида SS_tot=SS_reg+SS_res. По результатам вычислений делают вывод о силе связи или взаимного влияния изучаемых факторов.

Показатель детерминации демонстрирует цифровое значение доли вариации результативного признака объекта или события. При интерпретации величины R 2 коэффициента корреляции его представляют в процентном выражении.

К примеру, 0,847 2 = 0,7174 означает, что в 71,74% случаев при изменении факторного показателя результативный признак приобретает соответствующее значение. Уравнение отличает высокая точность при правильном подборе значений по шкале Чеддока-Снедекора.

Оставшиеся 28,26% показателя детерминации приходятся на неучтенные в модели факторы. При отсутствии заметной статистической связи между корреляционными коэффициентами переменных для вычисления асимптотического распределения используют уравнение х 2 (К-1), где К – количество влияющих факторов.

Средняя ошибка аппроксимации

В социологических исследованиях, медицинской статистике, эконометрике значения силы взаимного влияния или степени устойчивости зависимостей часто рассчитывают с использованием замены объектов родственными и упрощенными.

Такой метод научного поиска называют аппроксимацией. Она позволяет изучать количественные характеристики, качественные свойства, факторные признаки с большей точностью и меньшим уровнем погрешности.

В теории чисел с помощью аппроксимации исследуют диофантовы приближения. В геометрии метод замены применяют при рассмотрении пересекающихся ломаных кривых. В эконометрической дисциплине распространены вычисления с применением средней ошибки аппроксимации.

Так называют диапазон отклонений расчетных величин зависимой переменной от фактического значения. Метод имеет особое значение в уравнениях линейной бинарной регрессии.

Качественные характеристики результирующего или влияющего фактора в разных математических моделях оценивают с помощью средней либо абсолютной ошибки аппроксимации.

Не превышающее 5-7% погрешности значение свидетельствует о правильном подборе соотношения уравнения с исходными данными. Если средняя ошибка аппроксимации выходит за пределы указанного диапазона, формулу не используют для статистических вычислений.

Шкала Чеддока (коэффициент корреляции, отклоняющийся менее, чем на 1% от показателя 1,00 гласит о стойкой функциональной связи объектов, событий или свойств) позволяет приблизить объем совокупности к фактическому значению результативного признака.

Показатель всегда отличается от теоретической величины, рассчитанной с применением уравнения парной регрессии. В редких случаях ошибка аппроксимации изначально равна нулю. Допустимый предел погрешности составляет 8-10%.

Отрицательные значения

Любую вычисленную статистическую величину с коэффициентом корреляции подвергают математическому испытанию на достоверность. Совокупность наблюдений или массивов разнородных данных представляет собой определенную выборку, в которой есть погрешности.

Поэтому такие расчеты воспринимают не абсолютной истиной, а относительно точной оценкой влияющих факторов, качественных характеристик объектов, степени связи факторов.

Отрицательные значения при вычислениях с применением шкалы Чеддока типичны для регрессивных моделей, целью которых служит установление обратной связи между объектами исследования в точном цифровом выражении. Коэффициент корреляции в таких уравнениях может принимать значения от -1 до 0.

Видео о шкале Чеддока-Снедекора

Расчет коэффициента корреляции

Методы расчета коэффициента корреляции

При изучении различных социально-экономических явлений выделяют функциональную связь и стохастическую зависимость. Функциональная связь — это такой вид связи, при которой некоторому взятому значению факторного показателя соответствует лишь одно значение результативного показателя. Функциональная связь проявляется во всех случаях исследования и для каждой определенной единицы анализируемой совокупности.

Размещено на www.rnz.ru

В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.

Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:

Шкала Чеддока количественной оценки степени тесноты связи

Величина показателя тесноты связи	Характер связи
До |±0,3|	Практически отсутствует
|±0,3|-|±0,5|	Слабая
|±0,5|-|±0,7|	Умеренная
|±0,7|-|±1,0|	Сильная

При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.

Формула расчета коэффициента корреляции

В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента. Общая формула для расчета коэффициента корреляции имеет следующий вид:

Формула расчета коэффициента корреляции

где r — линейный коэффициент корреляции.

Опираясь на математические свойства средней, общую формулу можно представить следующим образом, получив следующее выражение:

Формула расчета линейного коэффициента парной корреляции

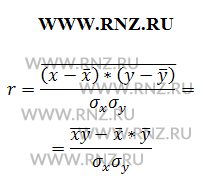
Выполняя дальнейшие преобразование, можно получить следующие формулы вычисления коэффициента корреляции Пирсона:

Формула расчета коэффициента корреляции Пирсона

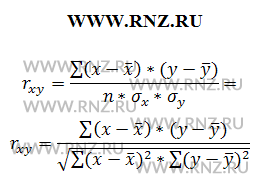
где n — число наблюдений.

Выполняя вычисление по итоговым данным для расчета показателя корреляции, его можно рассчитать с использованием следующих формул:

Пирсон онлайн

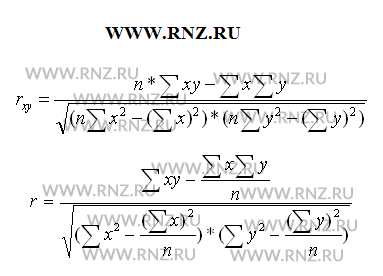
Методом расчета показателя корреляции является вычисление данного показателя с использованием его взаимосвязи с дисперсиями факторного и результативного признаков по следующей формуле:

Формула расчета коэффициента корреляции через дисперсии

Последние три приведенные формулы используются для изучения взаимосвязи между признаками в совокупностях незначительной величины — до 30 наблюдений.

Также показатель тесноты связи можно определить на основе его взаимосвязи с показателями уравнения регрессии, используя следующее отношение:

Формула расчета коэффициента корреляции через показатели регрессии

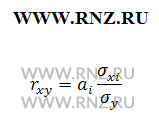
где а_i — коэффициент регрессии в уравнении связи;

σ_хi — среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

Линейный коэффициент корреляции несет в себе важную информацию для успешного изучения социально-экономических явлений и процессов, распределение которых близко к нормальному. Теоретически является обоснованным, что условие r_xy = 0 является необходимым и достаточным для того, чтобы факторный и результативный признаки x и y являлись независимыми. При указанном условии, когда показатель корреляции равен нулю, показатели регрессии также имеют нулевые значения, а прямые линии регрессии у по х и х по у являются взаимно перпендикулярными на графике (параллельными: одна прямая — оси х, а другая прямая — оси y).

В том случае, когда r_xy = 1, то это означает, что все точки (х, у) расположены на прямой и зависимость между х и у относится к функциональным. При указанном условии прямые линии регрессии совпадают. Указанное положение действует также в случае исследования трех и более показателей, если они подчинены закону нормального распределения.

В целом значение линейного показателя связи находится в диапазоне от — 1 до 1, т.е.: -1

Пример расчета коэффициента корреляции

Приведем пример расчета коэффициента корреляции Пирсона для значений, приведенных в следующей таблице. Для этого используем следующие данные (пример условный):

Значение показателя X	Значение показателя Y
1,1	1,3
1,9	1,1
1,5	1,2
1,9	0,5
1,9	1,5
1,1	1,7
0,9	2
1	0,9
1,3	1,2
1,5	1,7

Количество наблюдений менее 30, поэтому в нашем примере для расчета парного коэффициента корреляции используем следующую формулу:

Для этого составим вспомогательную таблицу:

№ п/п	X	Y	xy	x 2	y 2
1	1,1	1,3	1,43	1,21	1,69
2	1,9	1,1	2,09	3,61	1,21
3	1,5	1,2	1,8	2,25	1,44
4	1,9	0,5	0,95	3,61	0,25
5	1,9	1,5	2,85	3,61	2,25
6	1,1	1,7	1,87	1,21	2,89
7	0,9	2	1,8	0,81	4
8	1	0,9	0,9	1	0,81
9	1,3	1,2	1,56	1,69	1,44
10	1,5	1,7	2,55	2,25	2,89
Итого	14,1	13,1	17,8	21,25	18,87

Методология вычисления: r = (17,8-14,1*13,1/10)/(√((21,25-14,1*14,1/10)*(18,87-13,1*13,1/10))) = -0,4389.

Полученное значение коэффициента корреляции Пирсона говорит о наличии обратной связи между X и Y. Величина коэффициента корреляции Пирсона показывает, что связь между X и Y слабая.

Онлайн калькулятор расчета коэффициента корреляции

В заключении приводим небольшой онлайн калькулятор расчета коэффициента корреляции онлайн, используя который, Вы можете самостоятельно выполнить расчет значения коэффициента корреляции Пирсона и получить интерпретацию рассчитанного значения. При заполнении формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить расчет коэффициента корреляции онлайн быстро и точно. В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значения показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!

Онлайн-калькулятор расчета коэффициента корреляции:

Простейшая обработка данных. Линейная регрессия.

Лабораторная работа №1.

Простейшая обработка данных. Линейная регрессия.

Коэффициент корреляции. Его значимость

Цель: научиться находить коэффициент корреляции и определять его начимость; находить коэффициенты регрессии и строить уравнение регрессии.

Основные сведения

Парная регрессия – это уравнение связи двух переменных у и х:

где у – зависимая переменная (результат, отклик);

х – независимая, объясняющая переменная (фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия: .

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических у _x минимальна.

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и в:

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

.

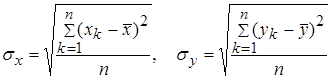
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r _xy для линейной регрессии

Теснота линейной связи между переменными может быть оценена на основании шкалы Чеддока:

Значение коэффициента корреляции при наличии:

Прямой связиОбратной связиСлабая0,1 – 0,3(– 0,3) – (– 0,1)Умеренная0,3 – 0,5(– 0,5) – (– 0,3)Заметная0,5 – 0,7(– 0,7) – (– 0,5)Высокая0,7 – 0,9(– 0,9) – (– 0,7)Весьма высокая0,9 – 1(– 1) – (– 0,9)

Положительное значение коэффициента корреляции говорит о положительной связи между х и у, когда с ростом одной из переменных другая тоже растет. Отрицательное значение коэффициента корреляции означает, с ростом одной из переменных другая убывает, с убыванием одной из переменной другая растет.

Оценку статистической значимости коэффициента корреляции проводят с помощью t-критерия Стьюдента. Выдвигают гипотезу Н₀ о статистически незначимом отличии коэффициента от нуля. Оценка значимости коэффициента корреляции с помощью t-критерия Стьюдента проводится путем сопоставления его значения с величиной случайной ошибки:

Стандартная (случайная) ошибка коэффициента корреляции определяется по формуле:

.

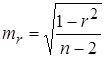
Сравнивая фактическое и табличное (критическое) значения t-статистики –t_табл. и t_факт. – принимает или отвергаем гипотезу Н₀.

Если t_табл. t_факт , то гипотеза Н₀ не отклоняется и признается случайная природа формирования коэффициента корреляции.

Порядок выполнения работы.

По заданной выборке исследовать зависимость результата у от фактора х. Для этого

1. Создать таблицу данных.

2. Найти средние значения , выборочные дисперсии исправленные средние квадратические отклонения .

3. Найти коэффициент корреляции и проверить его значимость.

4. Найти коэффициенты линейного уравнения регрессии.

5. Построить график прямой регрессии.

Пример выполнения лабораторной работы.

В табл. 1.1 приведены данные об объеме производства у (тыс.ед.) в зависимости от численности занятых х (тыс.чел.) некоторой фирмы.

x	11	13	15	18	20	22	24	25	27
y	15	17	21	20	28	33	34	32	29

1. В диапазоне В3:C11 подготовим исходные данные.

2. Вводим следующие формулы:

Ячейка	Формула	Примечание
D3	=B3*C3	Копируем диапазон D3:D11
E3	=B3*B3	Копируем диапазон E3:E11
F3	=C3*C3	Копируем диапазон F3:F11
B12	=СРЗНАЧ(B3:B11)	Копируем диапазон B12:F12
A17	=E12 – B12*B12	Выборочная средняя фактора
B17	=F12 – C12*C12	Выборочная средняя результата
A20	=СТАНДОТКЛОН(B3:B11)	Исправленное среднее квадратическое отклонение фактора
B20	=СТАНДОТКЛОН(С3:С11)	Исправленное среднее квадратическое отклонение результата

Получим следующие результаты (см. рис. 1.1).

Рис. 1.1. Результаты простейшей обработки данных

3. Для определения коэффициента корреляции воспользуемся формулой . Для этого в ячейку Е16 вводим формулу

=( D 12- B 12* C 12)/КОРЕНЬ( A 17* B 17)

Из расчетов следует, что коэффициент корреляции r=0,97. Это свидетельствует о том, что связь между объемом выпуска продукции и численностью занятых весьма высокая и положительная.

4. Для проверки значимости коэффициента корреляции введем вспомогательные данные:

К16 9 число предприятий;

К17 0,05 уровень значимости.

5. Далее вводим следующие формулы:

H19	=КОРЕНЬ((1-E16*E16)/(K16-2))	Стандартная ошибка
H20	=E16/H19	t — статистика
H21	=СТЬЮДРАСПОБР(K17;K16 – 2)	Критическое значение t — статистики
H22	=ЕСЛИ(ABS(H20)>H21; «Значим»; «Незначим»)	Вывод

Таким образом, получим данные, представленные на рис 1.2.

Рис. 1.2. Анализ значимости коэффициента корреляции

6. Для определения коэффициентов уравнения линейной регрессии на

следует в ячейки I3, I4 ввести соответственно следующие формулы:

=(D12-B12*C12)/A17;

=C12-I3*B12.

Значение коэффициента b=1,47 говорит о том, что при увеличении численности занятых на 1 тыс.чел. объем продукции увеличится на 1,74 тыс.ед.

Результаты расчетов приведены на рис.1.3.

Рис. 1.3. Результаты расчетов

7. Для построения графика выделим диапазон В3:С11. Вызовем Мастер диаграмм. Чтобы ось отражала фактические данные, выберем тип диаграммы Точечная. После чего нажмем кнопку Готово. На построенной диаграмме выделим график функции, щелкнув по нему левой кнопкой мыши. Выделение обозначается светлыми маркерами на функции. Нажав правую кнопку мыши, выведем контекстно-зависимое меню, в котором выберем опцию Добавить линию тренда. В окне Линия тренда по вкладке Тип выберем тип функции Линейная, а во вкладке Параметры – установим флажок показывать уравнение на диаграмме. В результате на диаграмме появиться вид теоретической кривой – тренда и ее уравнение (рис.1.4).

Рис. 1.4. Графики фактических данных и построенной регрессии

8. Вычисление параметров регрессии с помощью статистических функций Excel:

КОРРЕЛ(массив1;массив2) вычисляет коэффициент корреляции между двумя переменными; значения первой из них приведены в диапазоне массив1, значения второй – в диапазоне массив2;

НАКЛОН(известные_значения_y;известные_значения_x) служит для определения коэффициента b;

ОТРЕЗОК(известные_значения_y;известные_значения_x) служит для определения коэффициента a.

C27	=КОРРЕЛ(B3:B11;C3:C11)	Коэффициент корреляции
C28	=НАКЛОН(С3:С11;B3:B11)	Коэффициент b
C29	=ОТРЕЗОК(C3:C11;B3:B11)	Коэффициент a

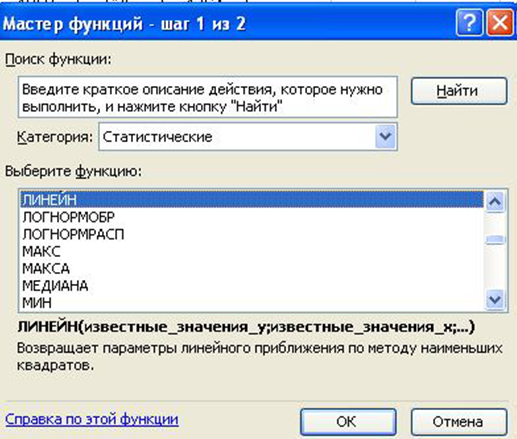
Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии. Порядок вычислений следующий:

1) выделите область пустых ячеек 5х2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики (А27:В3);

2) в главном меню выберите Вставка/Функция;

3) в строке Категория (рис.1.5) выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните ОК.

Рис. 1.5. Диалоговое окно «Мастер функций»

4) Заполните аргументы функции (рис.1.6.):

Известные_значения_у – диапазон, содержащий данные результативного признака;

Известные_значения_х – диапазон, содержащий данные факторов независимого признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0.

Статистика – логическое значение, которое указывает выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводится только оценки параметров уравнения. Далее ОК.

Рис.1.6. Диалоговое окно ввода аргументов функции ЛИНЕЙН

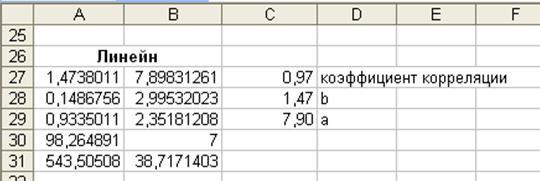
5) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL+SHIFT+ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента	Значение коэффициента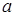
Среднеквадратическое отклонение	Среднеквадратическое отклонение
Коэффициент детерминации	Среднеквадратическое отклонение y
F — статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Результаты регрессионного анализа представлены на рис.1.7.

Рис. 1.7.Результаты регрессионного анализа

Индивидуальное задание к лабораторной работе №1

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции ( y ,млн. руб.) от объема капиталовложений ( x , млн. руб.)

1

2

3

4

5

6

7

8

9

10

1 1

1 2

1 3

1 4

1 5

№	1	2	3	4	5	6	7	8	9	10
x	66	58	73	82	81	84	55	67	81	59
y	133	107	145	162	163	170	104	132	159	116
x	72	52	73	74	76	79	54	68	73	64
y	121	84	119	117	129	128	102	111	112	98
x	38	28	27	37	46	27	41	39	28	44
y	69	52	46	63	73	48	67	62	47	67
x	36	28	43	52	51	54	25	37	51	29
y	104	77	117	137	143	144	82	101	132	77
x	31	23	38	47	46	49	20	32	46	24
y	38	26	40	45	51	49	34	35	42	24
x	33	17	23	17	36	25	39	20	13	12
y	43	27	32	29	45	35	7	32	22	24
x	36	28	43	52	51	54	25	37	51	29
y	85	60	99	117	118	125	56	86	115	68
x	17	22	10	7	12	21	14	7	20	3
y	26	27	22	19	21	26	20	15	30	13
x	12	4	18	27	26	29	1	13	26	5
y	21	10	26	33	34	37	9	21	32	14
x	26	18	33	42	41	44	15	27	41	19
y	43	28	51	62	63	67	26	43	61	33
x	66	58	73	82	81	84	55	67	81	59
y	133	107	145	162	163	170	104	132	159	116
x	72	52	73	74	76	79	54	68	73	64
y	121	84	119	117	129	128	102	111	112	98
x	38	28	27	37	46	27	41	39	28	44
y	69	52	46	63	73	48	67	62	47	67
x	36	28	43	52	51	54	25	37	51	29
y	104	77	117	137	143	144	82	101	132	77
x	31	23	38	47	46	49	20	32	46	24
y	38	26	40	45	51	49	34	35	42	24

Лабораторная работа №2

Основные сведения

Оценку качества построенной модели дает коэффициент (индекс) детерминации , а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

.

Допустимый предел значений средней ошибки аппроксимации – не более 8–10%.

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения раскладывается на две части – «объясненную» и «необъясненную»:

где – общая сумма квадратов отклонений; – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.

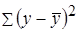
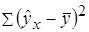
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F — критерия Фишера:

Фактическое значение F -критерия Фишера (1.9) сравнивается с табличным значением при уровне значимости α и степенях свободы k₁ = m и k₂ = n – m — 1. При этом, если фактическое значение F -критерия больше табличного, то признается статистическая значимость уравнения в целом.

Для парной линейной регрессии m = 1, поэтому

Величина F -критерия связана с коэффициентом детерминации , и ее можно рассчитать по следующей формуле:

В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: m _b и m _a .

Стандартная ошибка коэффициента регрессии определяется по формуле:

где 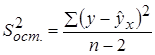– остаточная дисперсия на одну степень свободы.

Величина стандартной ошибки совместно с t – распределением Стьюдента при n — 2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t -критерия Стьюдента: которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы  (n — 2). Доверительный интервал для коэффициента регрессии определяется как .

Стандартная ошибка параметра a определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t -критерий: , его величина сравнивается с табличным значением при n — 2 степенях свободы. Доверительный интервал для коэффициента регрессии определяется как .

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, т.к. он не может одновременно принимать и положительное, и отрицательное значения.

Пример выполнения лабораторной работы.

1. В диапазоне А2:C11 подготовим исходные данные.

2. Введем вспомогательные данные:

Ячейка	Формула	Примечание
C16	9	Число предприятий
C17	0,05	Уровень значимости
C18	=ОТРЕЗОК(C3:C11;B3:B11)	Коэффициент a
C19	=НАКЛОН(С3:С11;B3:B11)	Коэффициент b
C20	=СРЗНАЧ(B3:B11)	Среднее значение фактора
C21	=СРЗНАЧ(C3:C11)	Среднее значение результата

Проверка значимости коэффициента b.

1) Для расчетов сумм квадратов отклонений введем формулы:

Ячейка	Формула	Примечание
D3	=$C$18+$C$19*B3	Копируем диапазон D3:D11
E3	=(C3 — D3)^2	Копируем диапазон E3:E11
F3	=(B3 — $C$20)^2	Копируем диапазон F3:F11
E12	=СУММ(E3:E11)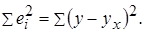
F12	=СУММ(F3:F11)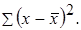

2) Стандартная ошибка параметра b определяется по формуле:

поэтому введем в ячейку D24 формулу:

=(E12/((C16-2)*F12))^0,5.

3) В ячейке D25 рассчитана t-статистика параметра b как отношение величины этого параметра к его стандартной ошибке:

=C19/D24.

4) Критическое значение t-статистики определим в ячейке D26 с помощью функции СТЬЮДРАСПОБР, у которой первым аргументом является пороговая значимость или вероятность (в нашем случае примем ее равной 0,05), а вторым – число степеней свободы (n–2=9–2=7). Таким образом, формула, введенная в D26, должна иметь вид:

=СТЬЮДРАСПОБР($C$17;$C$16-2).

5) Для того чтобы автоматически был получен вывод о значимости параметра b построим в ячейке D27 формулу:

=ЕСЛИ(ABS(D25)>D26;»Значим»;»Незначим»).

6) Для расчета доверительного интервала определяем предельную ошибку в ячейке D28:

=D26*D24.

7) Нижняя граница доверительного интервала в ячейке D29:

=C19-D28.

8) Верхняя граница доверительного интервала в ячейке D30:

=C19+D28.

Таким образом, доверительный интервал параметра b имеет вид (1,12; 1,83).

Проверка значимости коэффициента a .

Ячейка	Формула	Примечание
G3	=B3*B3	Копируем диапазон G3:G11
G12	=СУММ(E3:E11)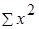
D33	=В24*КОРЕНЬ(G12/C16)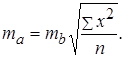
D34	=C18/D33	t – статистика параметра a
D35	=СТЬЮДРАСПОБР($С$17;$C$16– 2)	Критическое значение t — статистики
D36	=ЕСЛИ(ABS(D34)>D35; «Значим»; «Незначим»)
D37	= D35*D33	Предельная ошибка
D38	=C18-D37	Нижняя граница доверительного интервала
D39	=C18+D37	Верхняя граница доверительного интервала

Лабораторная работа №3

Основные сведения

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например

– полиномы различных степеней –

– равносторонняя гипербола –

– полулогарифмическая функция –

2. Регрессии, нелинейные по оцениваемым параметрам, например

– степенная –

– показательная –

– экспоненциальная – .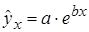

Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов.

Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).

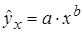
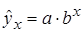
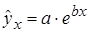
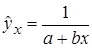
К внутренне линейным моделям относятся, например, степенная функция , показательная – , экспоненциальная – , обратная – .

К внутренне нелинейным моделям можно, например, отнести следующие модели: .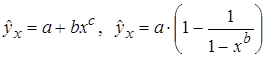

Приведем формулы для расчета параметров наиболее часто используемых типов уравнений регрессии (табл. 1.3):

Вид функции, y	Линеаризация	Параметры уравнения регрессии	Искомое уравнение
Степенная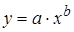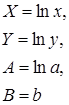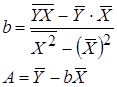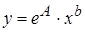
Показательная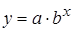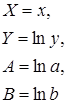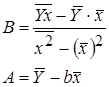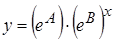
Обратная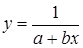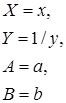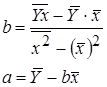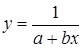
Полулогарифмическая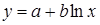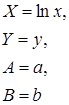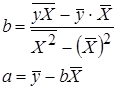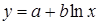
Гиперболическая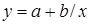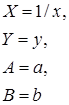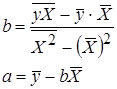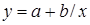
Экспоненциальная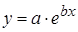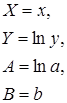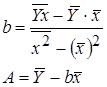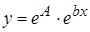

В случае нелинейной зависимости тесноту связи между величинами оценивают по величине корреляционного отношения:

Интервал изменения корреляционного отношения .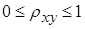

Оценку качества построенной модели дает индекс детерминации .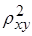

Коэффициент детерминации 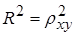– квадрат индекса корреляции –

характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у.

Чем ближе коэффициент детерминации к 1, тем выше качество уравнения регрессии, тем в большей мере оно объясняет поведение отклика.

Порядок выполнения работы.

Используя данные лабораторной работы №1, построить линейную, степенную, показательную, экспоненциальную, полулогарифмическую, гиперболическую и обратную модели и с помощью коэффициента детерминации сравнить эти модели. Для чего необходимо:

1. Найти уравнение регрессии.

2. Найти общую сумму квадратов отклонений и остаточную сумму квадратов отклонений.

3. Найти коэффициент детерминации.

4. Найти параметры регрессии с помощью статистической функции ЛИНЕЙН.

Пример выполнения лабораторной работы.

Создадим новую рабочую книгу с семью листами.

Название листа	Назначение
Линейная	Для анализа линейной модели
Степенная	Для анализа степенной модели
Показательная	Для анализа показательной модели
Обратная	Для анализа обратной модели
Полулогарифмическая	Для анализа полулогарифмической модели
Гиперболическая	Для анализа гиперболической модели
Экспоненциальная	Для анализа экспоненциальной модели

Будем использовать данные из лабораторной работы №1.

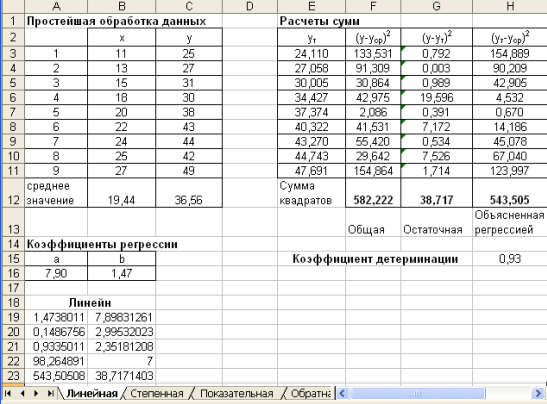
1. Лист Линейная оформим, как показано на рис.1.3:

Рис. 1.3. Лист Линейная

На этом листе коэффициенты линейной регрессии определяются с помощью статистических функций (см. лабораторную работу №1).

Для расчета сумм, которые понадобятся при определении коэффициента детерминации (и при выполнении следующей лабораторной работы), введем формулы:

Ячейка	Формула	Примечание
E3	=$A$16+$B$16*B3	Расчет теоретических значений результата . Копируем диапазон E3:E11
F3	=(C3–$C$12)^2	Копируем диапазон F3:F11
G3	=(C3–E3)^2	Копируем диапазон G3:G11
H3	=(E3-$C$12)^2	Копируем диапазон H3:H11
F12	=СУММ(F3:F11)	Копируем диапазон F12:H12

Замечание. В приведенных формулах неоднократно используется абсолютная адресация, содержащая знак «$». Это необходимо для того, чтобы при копировании формул данный адрес не изменялся. Для того чтобы превратить относительный адрес А16 в абсолютный ($A$16), достаточно нажать клавишу F4 в то время, когда курсор находится на ячейке А16.

Для вычисления коэффициента детерминации в ячейку Н15 введем формулу:

=1-G12/F12.

2. Регрессия в виде степенной функции имеет вид: .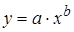

Для нахождения параметров регрессии 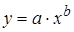необходимо провести ее линеаризацию:

Составляем вспомогательную таблицу для преобразованных данных (рис. 2.3):

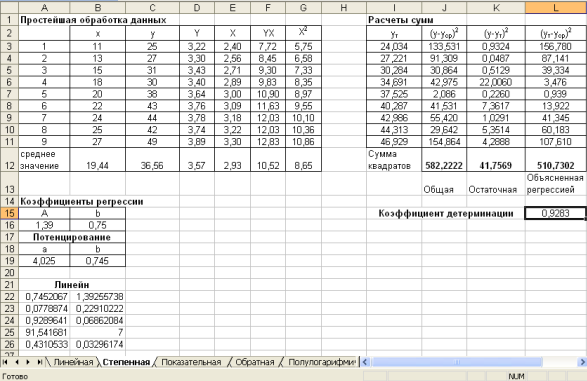
Рис. 2.3 Лист Степенная

Ячейка	Формула	Примечание
D3	=LN(C3)	Y=ln y Копируем диапазон D3:D11
E3	=LN(B3)	X=ln x Копируем диапазон E3:E11
F3	=D3*E3	Копируем диапазон F3:F11
G3	=E3^2	Копируем диапазон G3:G11
D12	=СРЗНАЧ(D3:D11)	Копируем диапазон D12:G12

Для вычисления коэффициентов регрессии введем следующие формулы:

Ячейка	Формула	Примечание
B16	=(F12-E12*D12)/(G12-E12^2)	b
A16	=D12-B16*E12	A

После потенцирования находим искомые коэффициенты регрессии:

Ячейка	Формула	Примечание
A19	=EXP(A16)	a
B19	= B16	b

Тогда уравнение регрессии будет иметь вид: .

Для расчета сумм введем формулы:

Ячейка	Формула	Примечание
I3	=$A$19*B3^$B$19	Расчет теоретических значений результата . Копируем диапазон I3:I11
J3	=(C3–$C$12)^2	Копируем диапазон J3:J11
K3	=(C3–E3)^2	Копируем диапазон K3:K11
L3	=(E3-$C$12)^2	Копируем диапазон L3:L11
J12	=СУММ(J3:J11)	Копируем диапазон J12:L12

Для вычисления коэффициента детерминации в ячейку L15 введем формулу:

=1-K12/J12.

Проведем расчеты параметров регрессии с помощью статистической функции ЛИНЕЙН.

Выделим диапазон А22:В26. введем формулу

=ЛИНЕЙН(D3:D11;E3:E11;1;1).

В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL+SHIFT+ENTER.

3. Расчеты на остальных листах во многом повторяют расчеты, произведенные на листе Степенная, поэтому остальные листы лучше всего получить копированием листа Степенная.

Для этого необходимо:

· находясь на листе Степенная, выделить его полностью, щелкнув мышью на пересечении названий столбцов и строк; с помощью кнопки (Копировать) скопировать лист в Буфер обмена;

· перейти на следующий лист и выделив ячейку А1,щелкнуть мышью по кнопке (Вставить).

Получим следующие результаты (рис. 3.3-7.3):

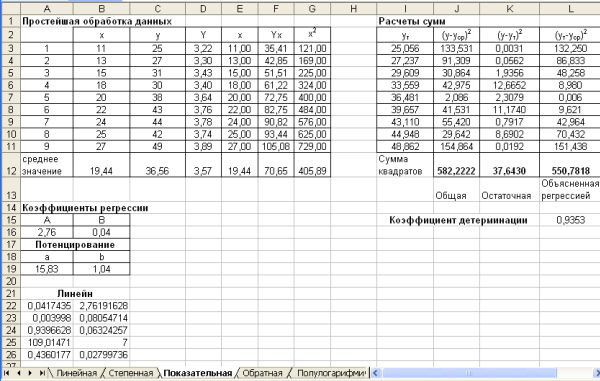
Рис. 3.3. Лист Показательная

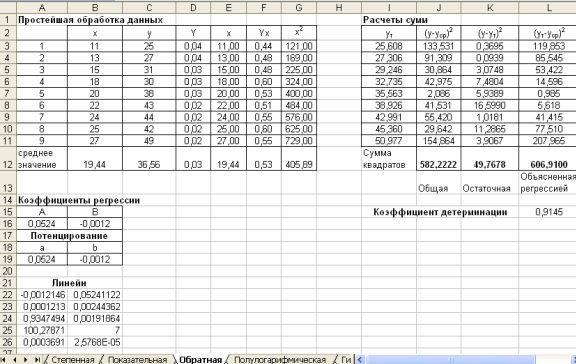
Рис. 4.3. Лист Обратная

Рис. 5.3. Лист Полулогарифмическая

Рис. 6.3. Лист Гиперболическая

Рис. 7.3. Лист Экспоненциальная

Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице (табл. 2.1).

Все уравнения регрессии достаточно хорошо описывают исходные данные. Некоторое предпочтение можно отдать показательной или экспоненциальной функции, для которых значение коэффициента детерминации наибольшее.

Название листа	Уравнение регрессии	Коэффициент детерминации
Линейная		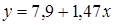0,9335
Степенная		0,9283
Показательная		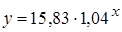0,9353
Обратная		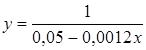0,9145
Полулогарифмическая		0,9060
Гиперболическая		0,8528
Экспоненциальная		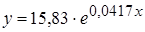0,9353

Лабораторная работа №4

Основные сведения.

Пусть по заданной выборке объема n найдено выборочное уравнение линейной регрессии

С помощью этого уравнения можно прогнозировать значение результата у р при определенном прогнозном значении фактора х р.

Прогнозное значение у р определяется путем подстановки в уравнение регрессии у=а+bх соответствующего прогнозного значения х р.

Точное уравнение регрессии нам неизвестно. Поэтому мы не можем сделать точный прогноз. Можно только утверждать, что прогнозное значение результата у р при данном х р с вероятностью γ попадет в доверительный интервал γр. Вероятность γ называется уровнем надежности.

Ошибка прогноза составляет:

,

где — стандартная ошибка регрессии (дисперсия ошибки или остаточная дисперсия).

Предельная ошибка прогноза, составит:

.

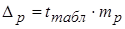
Доверительный интервал прогноза:

.

Точность прогноза можно оценить с помощью относительной ошибки прогноза:

Порядок выполнения работы.

Используя данные к лабораторной работе №1 при х р=20:

1. найти уравнение регрессии;

2. рассчитать доверительный интервал прогноза при значениях уровня надежности 80%, 90%, 95%;

3. найти относительную ошибку прогноза;

4. построить графики линии регрессии с доверительными границами.

Пример выполнения лабораторной работы.

Расчеты для каждого из уровней надежности производить на отдельных листах, которые назовем , соответственно: 80%, 90%, 95%.

I. Лист 80%.

5. В диапазоне А2:C11 подготовим исходные данные.

6. В ячейку В12 запишем значение хр=15,5, для которого необходимо спрогнозировать значение результата ур.

7. Вводим следующие формулы:

8. Для графического представления полученных результатов:

· Вводим следующие формулы:

Таким образом получим данные, представленные на рис. 1.4.

· Выделим одновременно диапазоны В2:С11, E2:E11, H2:I11 (поскольку эти диапазоны несмежные, при этом должна быть нажата клавиша Ctrl);

· Вызовем Мастер диаграмм. Чтобы ось отражала фактические данные, выберем тип диаграммы Точечная;

· Для добавления на диаграмму прогнозируемых значений в Мастере диаграмм на шаге 2 перейдем на вкладку Ряд (рис. 2.4). Щелкнем по кнопке Добавить и введем с помощью левой кнопки мыши: Имя − Прогноз, Значения Х – В12, Значения Y – С29. Щелкнув по кнопке Готово, получим диаграмму, представленную на рисунке 3.4.

Отформатируем диаграмму. Для этого щелкнем дважды по фону и выберем заливку прозрачная, затем щелкнем дважды по линии регрессии и выберем тип линии, цвет и толщину, а переключатель маркера поставим в положение отсутствует. Аналогичным образом форматируются линии, представляющие границы доверительных интервалов, и точки, отображающие прогнозируемые значения. В итоге получим диаграмму, представленную на рис. 4.4.

II. Лист 90% и 95%.

Чтобы получить расчеты для уровней надежности 90% и 95%, достаточно скопировать лист 80% на листы 90% и 95% и ввести на них в ячейку С21 соответственно значения 0,9 и 0,95. При этом диаграммы, полученные при таком копировании, следует удалить и построить заново на основе расчетов, полученных на листах 90% и 95% (рис. 5.4 и 6.4).

Рис. 1.4. Прогнозирование на основании линейной модели при уровне

Рис. 2.4. Шаг 2 Мастера диаграмм

Рис. 3.4. Диаграмма, построена с помощью Мастера

Рис. 4.4. Итоговый вид диаграммы при уровне надежности 80%

Рис. 5.4. Прогнозирование на основании линейной модели при уровне

Рис. 6.4. Прогнозирование на основании линейной модели при уровне

Сравним относительные погрешности прогнозов при различных уровнях надежности, для х р=15,5:

Повышение уровня надежности с 80% до 95% снижает точность прогноза в 19,6/11,7≈1,68 раза.

Лабораторная работа №1.

Простейшая обработка данных. Линейная регрессия.

Последнее изменение этой страницы: 2019-04-20; Просмотров: 718; Нарушение авторского права страницы

🎥 Видео