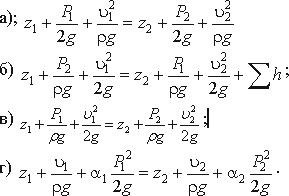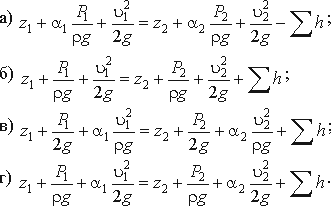Коэффициент кориолиса в уравнении бернулли характеризует режим течения жидкости (8 видео)

Содержание

Коэффициент кориолиса в уравнении бернулли характеризует режим течения жидкости
Коэффициент кориолиса в уравнении бернулли характеризует режим течения жидкости
Гидродинамика. Уравнение Бернулли для потока реальной жидкости.
Режимы движения жидкости
📸 Видео

Видео:Коэффициент КориолисаСкачать

Коэффициент кориолиса в уравнении бернулли характеризует режим течения жидкости

Уравнение Бернулли для реальной и идеальной жидкости

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления

Задача. Пример решения уравнения Бернулли

По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве

Точка 1 – это место где известно давление

Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.

Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.

Что такое идеальная жидкость?

Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.

Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.

Формула Бернулли для реальной жидкости

Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.

Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса

Что такое коэффициент Кориолиса?

Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.

Чему равен коэффициент Кориолиса?

Нд.п. – Это динамические потери. Это потери вызванные движением воды.

Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:

Посмотрите видеоурок по составлению уравнения Бернулли:

Как сделать гидравлический расчет погружного насоса?

Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Коэффициент кориолиса в уравнении бернулли характеризует режим течения жидкости

3.1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется

а) открытым сечением;
б) живым сечением;
в) полным сечением;
г) площадь расхода.

3.2. Часть периметра живого сечения, ограниченная твердыми стенками называется

а) мокрый периметр;
б) периметр контакта;
в) смоченный периметр;
г) гидравлический периметр.

3.3. Объем жидкости, протекающий за единицу времени через живое сечение называется

а) расход потока;
б) объемный поток;
в) скорость потока;
г) скорость расхода.

3.4. Отношение расхода жидкости к площади живого сечения называется

а) средний расход потока жидкости;
б) средняя скорость потока;
в) максимальная скорость потока;
г) минимальный расход потока.

3.5. Отношение живого сечения к смоченному периметру называется

а) гидравлическая скорость потока;
б) гидродинамический расход потока;
в) расход потока;
г) гидравлический радиус потока.

3.6. Если при движении жидкости в данной точке русла давление и скорость не изменяются, то такое движение называется

а) установившемся;
б) неустановившемся;
в) турбулентным установившимся;
г) ламинарным неустановившемся.

3.7. Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени называется

а) ламинарным;
б) стационарным;
в) неустановившимся;
г) турбулентным.

3.8. Расход потока обозначается латинской буквой

3.9. Средняя скорость потока обозначается буквой

3.10. Живое сечение обозначается буквой

3.11. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется

а) траектория тока;
б) трубка тока;
в) струйка тока;
г) линия тока.

3.12. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется

а) трубка тока;
б) трубка потока;
в) линия тока;
г) элементарная струйка.

3.13. Элементарная струйка — это

а) трубка потока, окруженная линиями тока;
б) часть потока, заключенная внутри трубки тока;
в) объем потока, движущийся вдоль линии тока;
г) неразрывный поток с произвольной траекторией.

3.14. Течение жидкости со свободной поверхностью называется

а) установившееся;
б) напорное;
в) безнапорное;
г) свободное.

3.15. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется

а) безнапорное;
б) напорное;
в) неустановившееся;
г) несвободное (закрытое).

3.16. Уравнение неразрывности течений имеет вид

3.17. Уравнение Бернулли для идеальной жидкости имеет вид

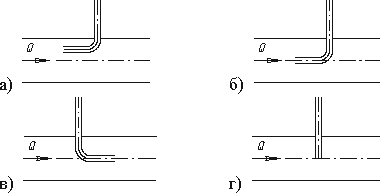
3.18. На каком рисунке трубка Пито установлена правильно

3.19. Уравнение Бернулли для реальной жидкости имеет вид

3.20. Член уравнения Бернулли, обозначаемый буквой z, называется

а) геометрической высотой;
б) пьезометрической высотой;
в) скоростной высотой;
г) потерянной высотой.

3.21. Член уравнения Бернулли, обозначаемый выражением 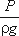называется

а) скоростной высотой;
б) геометрической высотой;
в) пьезометрической высотой;
г) потерянной высотой.

3.22. Член уравнения Бернулли, обозначаемый выражением 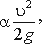называется

а) пьезометрической высотой;
б) скоростной высотой;
в) геометрической высотой;
г) такого члена не существует.

3.23. Уравнение Бернулли для двух различных сечений потока дает взаимосвязь между

а) давлением, расходом и скоростью;
б) скоростью, давлением и коэффициентом Кориолиса;
в) давлением, скоростью и геометрической высотой;
г) геометрической высотой, скоростью, расходом.

3.24. Коэффициент Кориолиса в уравнении Бернулли характеризует

а) режим течения жидкости;
б) степень гидравлического сопротивления трубопровода;
в) изменение скоростного напора;
г) степень уменьшения уровня полной энергии.

3.25. Показание уровня жидкости в трубке Пито отражает

а) разность между уровнем полной и пьезометрической энергией;
б) изменение пьезометрической энергии;
в) скоростную энергию;
г) уровень полной энергии.

3.26. Потерянная высота характеризует

а) степень изменения давления;
б) степень сопротивления трубопровода;
в) направление течения жидкости в трубопроводе;
г) степень изменения скорости жидкости.

3.27. Линейные потери вызваны

а) силой трения между слоями жидкости;
б) местными сопротивлениями;
в) длиной трубопровода;
г) вязкостью жидкости.

3.28. Местные потери энергии вызваны

а) наличием линейных сопротивлений;
б) наличием местных сопротивлений;
в) массой движущейся жидкости;
г) инерцией движущейся жидкоcти.

3.29. На участке трубопровода между двумя его сечениями, для которых записано уравнение Бернулли можно установить следующие гидроэлементы

а) фильтр, отвод, гидромотор, диффузор;
б) кран, конфузор, дроссель, насос;
в) фильтр, кран, диффузор, колено;
г) гидроцилиндр, дроссель, клапан, сопло.

3.30. Укажите правильную запись

3.31. Для измерения скорости потока используется

а) трубка Пито;
б) пьезометр;
в) вискозиметр;
г) трубка Вентури.

3.32. Для измерения расхода жидкости используется

а) трубка Пито;
б) расходомер Пито;
в) расходомер Вентури;
г) пьезометр.

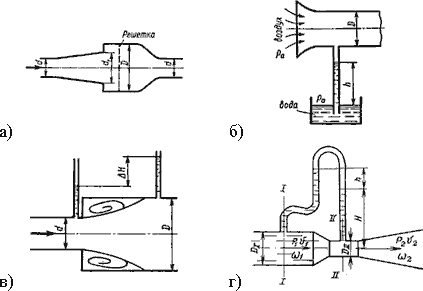
3.33. Укажите, на каком рисунке изображен расходомер Вентури

3.34. Установившееся движение характеризуется уравнениями

3.35. Расход потока измеряется в следующих единицах

3.36. Для двух сечений трубопровода известны величины P₁, υ₁, z₁ и z₂. Можно ли определить давление P₂ и скорость потока υ₂?

а) можно;
б) можно, если известны диаметры d₁ и d₂;
в) можно, если известен диаметр трубопровода d₁;
г) нельзя.

3.37. Неустановившееся движение жидкости характеризуется уравнением

3.38. Значение коэффициента Кориолиса для ламинарного режима движения жидкости равно

3.39. Значение коэффициента Кориолиса для турбулентного режима движения жидкости равно

3.40. По мере движения жидкости от одного сечения к другому потерянный напор

а) увеличивается;
б) уменьшается;
в) остается постоянным;
г) увеличивается при наличии местных сопротивлений.

3.41. Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Гидродинамика. Уравнение Бернулли для потока реальной жидкости.

При трансформации закономерности Бернулли для идеальной жидкости к уравнению потока реальной жидкости требуется принимать во внимание неравномерность разделения скоростей по сечению потока и потери энергии жидкости на внутреннее трение, что объясняется вязкостью жидкости.

В реальной жидкости вязкость формирует сопротивление движению жидкости. Это вызывает появление дополнительных потерь напора (энергии потока).

Распределение скоростей элементарных струек в потоке обычно величины не определенные, для этого в уравнение Бернулли добавляют поправочный коэффициент α.

Коэффициент α принято называть коэффициентом кинетической энергии или коэффициентом Кориолиса. Он характеризует неравномерное распределение скоростей в живом сечении потока, и равняется соотношению кинетической энергии, рассчитанной по реальным скоростям сечения, к той же энергии, вычисленной по средней скорости в этом же сечении потока. Следовательно, указанный коэффициент применяется для преобразования результатов расчетов по средней скорости в соответствие с реальными скоростями.

При турбулентном типе (со значительным перемешиванием, выравнивающим скорости на всех участках потока) кинетическая энергия практически равна полученной через среднюю скорость. Среднее значение коэффициента α берем на промежутке 1,05 – 1,11.

При ламинарном типе (перемешивание отсутствует) неравномерность поля скоростей достаточно велика и кинетическая энергия в 2 раза больше, чем вычисленная по средней скорости, α = 2.

Формула Бернулли для двух сечений потока реальной жидкости записывают так:

Закономерность Бернулли для потока реальной жидкости с физической точки зрения демонстрирует уравнение энергетического баланса. Теряемая энергия трансформируется в тепловую.

Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Режимы движения жидкости

Наука о движении жидкостей под действием внешних сил и о механическом взаимодействии жидкости и соприкасающихся с нею тел при их относительном движении называется гидродинамикой. Рассмотрим некоторые понятия и определения гидродинамики. Поток жидкости — ряд элементарных струек, движущихся в одном направлении в трубе. Живое сечение потока — перпендикулярное к основному направлению движения потока его поперечное сечение. Смоченный периметр — периметр поперечного сечения трубы, с которым соприкасается поток жидкости. Расход жидкости — количество жидкости, протекающей через живое сечение потока в единицу времени. Определяется по формуле Q = Fv, где F — площадь живого сечения, м 2 ; v — скорость движения жидкости, м/с.

Установившееся течение — основные параметры (скорость и давление) потока жидкости в любой точке потока не изменяются во времени. Неустановившееся течение — скорость и давление в определенных точках потока жидкости непостоянные, т. е. меняются во времени. Равномерное течение осуществляется в потоке, имеющем по длине одинаковые живые сечения, при этом в соответствующих точках сечений скорости и давления одинаковы. Неравномерное течение — живое сечение по длине потока жидкости меняется или скорости и давления в живых сечениях распределяются неодинаково.

Существуют два режима течения реальной капельной жидкости: ламинарный (струйный) и турбулентный (вихревой). Когда отдельные слои жидкости при малых скоростях движения перемещаются независимо (обособленно) друг от друга, т. е. наблюдается стройное, а именно послойное движение жидкости, — режим называется ламинарный. После достижения определенной скорости движения жидкости слоистое течение ее нарушается и движение становится беспорядочным, бесформенным — турбулентным.

Английским ученым О. Рейнольдсом было доказано, что характер течения зависит от соотношения между скоростью потока, диаметром трубы и вязкостью жидкости. Безразмерный параметр, называемый числом или критерием Рейнольдса, определяется по выражению Re = vd/v, где v — средняя скорость потока, м/с; d — внутренний диаметр трубы, м; v — коэффициент кинематической вязкости, м 2 /с.

Переход из ламинарного режима в турбулентный (и наоборот) происходит при определенном критическом числе Рейнольдса. При значении Re меньше критического движение потока жидкости ламинарное, при значении больше критического — турбулентное. Ламинарному режиму течения жидкости по гладким металлическим цилиндрическим трубам соответствуют значения Re 2200÷2300. В судовых системах встречаются все виды движения жидкости.

При течении сплошного потока несжимаемой жидкости и установившемся движении в трубе, ограниченной твердыми стенками, расход жидкости в любом живом сечении трубы есть величина постоянная:
Q = F1v1 = F2v2 — · · · = Fnvn = const, (1.2)
где F1 и F2 — площади разных сечений трубы; v1 и v2 — средние скорости течения жидкости в данном сечении трубы.

Уравнение (1.2) называется уравнением сплошности или неразрывности.

К установившемуся сплошному потоку несжимаемой идеальной жидкости, протекающей в жесткой трубе, применим закон сохранения энергии, т. е. энергия любой частицы струйки потока в любом его живом сечении есть величина постоянная и равна Еу = const, где Еу — энергия единицы массы (1 кг) текущей жидкости, или удельная энергия. В общем виде удельная энергия состоит из двух составляющих:
Еу = Еп + Ек, (1.3)
где Еп — потенциальная энергия; Ек — кинетическая энергия. В свою очередь, Еп — z + p/ρ, где z — удельная энергия положения выделенной единицы массы относительно какой-либо плоскости сравнения, называемая геометрическим напором.

В различных живых сечениях потока геометрический напор может иметь разные значения. Энергия положения характеризует работу, которую может произвести масса 1 кг выделенной жидкости при свободном падении с данной высоты. Единица геометрического напора выражается высотой столба жидкости в метрах. Вторая составляющая уравнения (1.3) является удельной энергией давления, т. е. потенциальной энергией 1 кг жидкости, создаваемой гидростатическим давлением, и называется пьезометрическим напором.

Избыточный гидростатический напор
p = ρh, (1.4)
где ρ — плотность жидкости; h — высота свободной поверхности жидкости от центра данного сечения. Из (1.4) следует, что h — = р/ρ. В рассматриваемых живых сечениях величина пьезометрических напоров равна
h1= p/ρ, h2 = p2/ρ, · · · , hн = pн/ρ (1.5)
Кинетическая энергия жидкости Ек = 0,5mv2. Отнесенная к 1 кг массы жидкости, т. е. когда m = 1 /g, кинетическая энергия (скоростной напор) равна Ек = v2/(2g). Величина Ек может измеряться высотой столба жидкости. Это следует из определения скорости свободно падающего тела v — √ 2ghc, откуда hс = v2/(2g)- Поэтому hc — это высота, падая с которой в среде, не имеющей сопротивления, 1 кг жидкости приобретает скорость v. В рассматриваемых живых сечениях потока скоростные напоры будут соответственно равны
Уравнение (1.7) называется уравнением Бернулли. Согласно этому уравнению полная удельная энергия идеальной жидкости в любом живом сечении элементарной струйки постоянна.

Рис. 1.1. К выводу уравнения Бернулли для идеальной жидкости

Рис. 1.2. Схема истечения жидкости из резервуара

На рис. 1.1 показаны картина истечения идеальной жидкости из резервуара по наклонной трубе переменного сечения (диаметры d1, d2, d3) и положение линий а—b—с—d—е—g, характеризующих энергетическое соотношение в различных сечениях потока. Так, в любом сечении трубы диаметром d1 кинетическая энергия (скоростной напор) жидкости hc1 больше кинетической энергии (скоростного напора) hс2 в любых сечениях трубы диаметром d2, тогда как потенциальная энергия (пьезометрический напор) h2 > h1.

Уравнение Бернулли можно истолковать и чисто геометрически. В самом деле, каждый член этого уравнения имеет линейную размерность. На рис. 1.1 можно заметить, что z1 и z2 — геометрические высоты сечений 1—1 и 2—2 над плоскостью сравнения, обозначенной условно 0—0; h1 и h2, а также hc1 и hc2 — соответственно пьезометрические и скоростные высоты в указанных сечениях.

При движении реальной (вязкой) жидкости скорости в сечении потока будут различны, что изменит значение энергии жидкости, проходящей в единицу времени через сечение потока. Неравномерность скоростей по сечению потока учитывается коэффициентом Кориолиса а, который равен 1,05—1,1 и в расчетах часто опускается.

Помимо учета неравномерности распределения скоростей по сечению потока для реальной жидкости необходимо учитывать потери напора на преодоление сопротивлений, которые обозначим hw. Тогда уравнение (1.7) примет вид
z1 + p1/ρ + a1v21/(2g) = z2 + p2/ρ + a2v22/(2g) + hw. (1.8)
Потеря напора hw при движении жидкости по трубопроводам, в свою очередь, состоит из потери напора по длине трубопровода hT и потери местных сопротивлений hм, т. е. hw = hт + hм.

Пользуясь уравнением Бернулли, рассмотрим случай установившегося течения жидкости по трубопроводу постоянного диаметра, присоединенному к резервуару, в котором поддерживается постоянное давление р2 и площадь сечения которого во много раз больше сечения трубопровода (v1v2 ≈ 0). Пусть в выходном сечении трубопровода действует постоянное давление р2 (рис. 1.2). Тогда на основании уравнения Бернулли можем написать z1 + (p1 — p2)/ρ = H = v2/(2g) или v = √2gR.

Контрольные вопросы
1. Какие вы можете дать определения понятиям «судовое устройство», «судовая система», «вспомогательный механизм»?

2. Какие свойства реальных жидкостей вы знаете?

3. Что такое вязкость и в каких единицах она измеряется?

4. Какие режимы течения реальной капельной жидкости вы знаете? Что такое критерий Рейнольдса и его значение при переходе от ламинарного режима к турбулентному?

5. Какой физический смысл имеет уравнение Бернулли?

6. Что такое расход жидкости и по какой формуле он определяется?

7. В чем отличие геометрического напора от гидростатического?