Коэффициент кориолиса в уравнении бернулли

Видео:Коэффициент КориолисаСкачать

Коэффициент кориолиса в уравнении бернулли

Уравнение Бернулли для реальной и идеальной жидкости

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления

Задача. Пример решения уравнения Бернулли

По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве

Точка 1 – это место где известно давление

Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.

Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.

Что такое идеальная жидкость?

Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.

Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.

Формула Бернулли для реальной жидкости

Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.

Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса

Что такое коэффициент Кориолиса?

Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.

Чему равен коэффициент Кориолиса?

Нд.п. – Это динамические потери. Это потери вызванные движением воды.

Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:

Посмотрите видеоурок по составлению уравнения Бернулли:

Как сделать гидравлический расчет погружного насоса?

Видео:Закон БернуллиСкачать

Энергетический смысл уравнения Бернулли

Определения

Элементарная струйка – струйка жидкости, боковая поверхность которой образована линией тока, проходящей через бесконечно малый замкнутый контур. Распределение скоростей по поперечному сечению элементарной струйки считается равномерным, по причине малости площади поперечного сечения, поэтому коэффициент Кориолиса 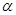равен единице.

Идеальная жидкость – модель жидкости, применяемая для расчётов реальных гидродинамических процессов.

Для идеальной жидкости приняты следующие допущения:

· отсутствуют касательные напряжения между слоями жидкости, следовательно,

отсутствует вязкость жидкости, следовательно, отсутствует трение между слоями жидкости, следовательно, в жидкости отсутствуют потери напора;

· жидкость является не сжимаемой;

· в жидкости отсутствует теплопроводность, т.е. жидкость не изменяет свой объём при изменении температуры;

· поток жидкости является сплошным, т.е. в жидкости отсутствуют места пустот или переуплотнений.

Виды уравнения Бернулли

Для элементарной струйки идеальной жидкости

Для элементарной струйки коэффициент Кориолиса равен единице, в идеальной жидкости отсутствуют потери, поэтому уравнение Бернулли будет иметь вид:

(1)

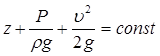
Для потока реальной жидкости

Для потока жидкости коэффициент Кориолиса будет иметь значение отличное от единицы, и зависеть от режима течения, для ламинарного режима α = 2, для турбулентного режима α = 1,05-1,1. Реальная жидкость имеет вязкость, следовательно, в реальной жидкости будут потери напора, поэтому уравнение Бернулли будет иметь вид:

Геометрический смысл уравнения Бернулли

Рассмотрим уравнение Бернулли для элементарной струйки идеальной жидкости (1).

В уравнении (1) все три слагаемых имеют линейную размерность [м]. Соответственно каждую высоту можно представить в виде реальных отрезков:

геометрическая высота, представляет собой расстояние от оси элементарной струйки (трубопровода) до поверхности земли.

пьезометрическая высота, показывает на какую высоту, может подняться жидкость под действием избыточного давления в данной точке, при условии, что на свободную поверхность действует давление внешней газообразной среды (т.е. атмосферное давление).

скоростная высота, показывает высоту, при падении с которой, частица жидкости достигла бы скорости .

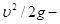
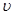
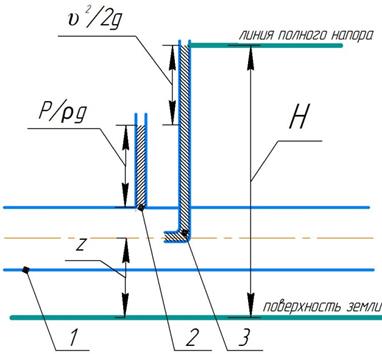
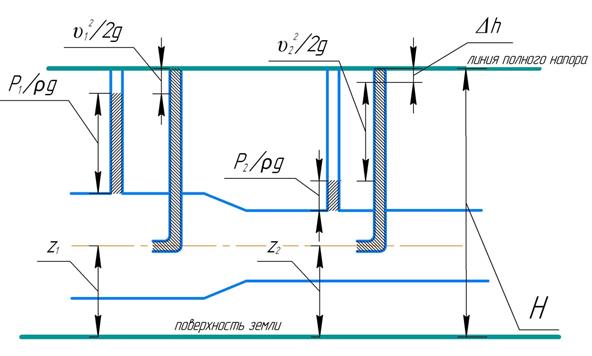
Рис. 1 Иллюстрация геометрического смысла уравнения Бернулли.

1 – элементарная струйка; 2 – пьезометр; 3 – трубка Пито (прибор для измерения скоростной высоты).

Геометрический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх слагаемых уравнения Бернулли остаётся величиной постоянной и равной величине полного напора Н [м].

(2)

Энергетический смысл уравнения Бернулли

Умножим каждое слагаемое уравнения (2) на величину ускорения свободного падения:

В итоге получаем слагаемые, который можно описать с точки зрения энергии:

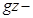
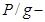
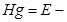
где удельная потенциальная энергия положения, т.е. если поднять жидкость массой 1 кг на высоту , то она будет иметь потенциальную энергию ;

удельная потенциальная энергия давления;

удельная кинетическая энергия;

полная удельная механическая энергия элементарной струйки.

Энергетический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх удельных энергий остаётся величиной постоянной и равной величине полной удельной механической энергии Е [Дж]. Возможна и другая формулировка: уравнение Бернулли – это есть закон сохранения энергии для элементарной струйки (потока) жидкости, который отображает взаимный переход кинетической и потенциальной энергии.

Потери

В потоке реальной жидкости в уравнение Бернулли добавляется слагаемое 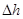, которое

представляет собой величину потерь напора. Запишем уравнение Бернулли для двух произвольных сечений потока жидкости:

С геометрической точки зрения потери отображаются отрезком, расположенным над скоростным напором, при этом потери отображаются во втором сечении.

Рис. 2. Иллюстрация потерь напора.

С энергетической точки зрения 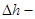это величина, показывающая, сколько энергии жидкость тратит на преодоление различных сопротивлений при переходе из первого сечения во второе сечение.

6. Порядок проведения расчётов:

1. Определить величину расхода жидкости:

2. Поскольку диаметры d₁=d₃, дальнейшие расчёты для широких частей трубопровода будут одинаковы. Поэтому будем проводить расчёт для одной широкой части трубопровода, при этом параметры жидкости, обозначая через индекс _1-3

Определить площади поперечного сечения трубопроводов S_1-3, S₂ [м];

3. Определить скорость течения жидкости:

4. Определить режим течения жидкости:

5. Определить величины скоростного напора: ;

6. На листе А4 построить график, зависимости изменения пьезометрического напора от

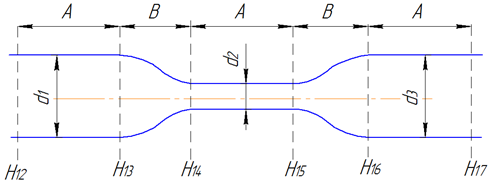
длины сечения трубопровода.По оси Х откладываются расстояния между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см

Рис. 3 Условное изображение исследуемого

трубопровода с точками подключения пьезометров.

По оси Y откладываются показания соответствующих пьезометров. В результате получится шесть точек, который соединяются ломаной линией. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

7. На листе А4 построить график, зависимость изменения скоростного напора от длины

сечения трубопровода.По оси Х откладывается расстояние между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см.

По оси Y откладываются значения скоростного напора. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

8. Вывод о работе с описанием графиков

Таблица 1. Результаты опыта

Видео:Уравнение Бернулли гидравликаСкачать

Названия и энергетический смысл напоров, входящих в уравнение Бернулли.

Геометрический напор(ρ g h) — характеризует удельную потенциальную энергию положения в данной точке ( данном сечении).

Статический напор (p) — ( пьезометрический) напор, характеризует удельную потенциальную энергию давления.

Скоростной ( динамический) напор (рν 2 /2) — удельная кинетическая энергия.

17.Коэффициент Кориолиса в уравнении Бернулли. С какой целью он добавлен в это уравнение? Каковы его значения для ламинарного и турбулентного потоков?

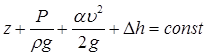
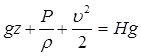
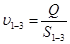
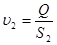
, коэффициент Кориолиса является отношением кинетической энергии потока, вычисленной по настоящему распределению скоростей в сечении, к кинетической энергии, определенной по значению средней скорости, он называется коэффициентом кинетической энергии. Пример: Рассмотрим поток, состоящий из двух ручьев, скорости которых соответственно равны: , Действительная кинетическая энергия равна сумме кинетических энергий ручьев: , Средняя скорость: . Тогда, кинетическая энергия потока, вычисленная по средней скорости: 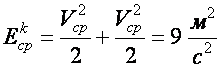. Коэффициент Кориолиса . Как видно, действительная кинетическая энергия больше средней, а коэффициент Кориолиса всегда больше единицы. Чем больше неравномерность распределения скоростей в поперечных сечениях потока, тем коэффициент Кориолиса имеет большее значение. Для ламинарного потока жидкости в трубах , а для турбулентного . То есть при турбулентном потоке скорости в сечении распределены более равномерно, чем при ламинарном потоке.

Дата добавления: 2015-02-16 ; просмотров: 15 | Нарушение авторских прав

💡 Видео

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Что такое сила Кориолиса?Скачать

Видео 6 Понятие о силе КориолисаСкачать

10. Уравнения БернуллиСкачать

Сила КориолисаСкачать

Уравнение Бернулли Метод БернуллиСкачать

Расчет водоснабжения и отопления с уравнением БернуллиСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Что такое сила Кориолиса?Скачать

Сложение ускорений точки. Ускорение КориолисаСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Галилео. Эксперимент. Закон БернуллиСкачать