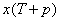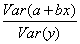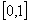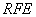Коэффициент a1 уравнения yi a0 a1xi et равен своему математическому ожиданию если (8 видео)

Содержание

Коэффициент a1 уравнения yi a0 a1xi et равен своему математическому ожиданию если
Эконометрика (часть 1-1)
Ниже указаны кнопки, нажмите на ту соц. сеть или месенджер, который Вы используете или заполните форму для того, чтобы мы ответили Вам на e-mail.
Ответы по гос эконометрике
Эконометрика.doc
📹 Видео

Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Коэффициент a1 уравнения yi a0 a1xi et равен своему математическому ожиданию если

136. Как правило в эталонной категории
• все фиктивные переменные равны 0

137. Категория — это событие, которое определенно __________________ в каждом наблюдении.
• либо происходит, либо нет

138. Когда делается предсказание на момент времени 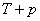, предполагается, что известна величина
•

139. Коэффициент R 2 вычисляется по формуле: R 2 = .
•

140. Коэффициент автокорреляции 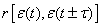случайных остатков в модели АР (1) равен:
•

141. Коэффициент автокорреляции определяется соотношением: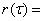
•

142. Коэффициент автокорреляции члена ряда 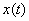с самим собой равен:
• 1

143. Коэффициент детерминации R 2 изменяется в пределах
•

144. Коэффициент детерминации равен __________________ выборочной корреляции между y и a + bx.
• квадрату

145. Коэффициент наклона в уравнении линейной регрессии показывает __________________ изменяется y при увеличении x на одну единицу.
• на сколько единиц

146. Коэффициент ранговой корреляции имеет дисперсию
• 1/ (n — 1)

147. Коэффициент Тейла лежит в пределах
• от 0 до 1

148. Коэффициент Тейла основан на расчете
• среднеквадратичного значения ошибки прогноза приростов

149. Коэффициент Тейла служит критерием
• успешности сделанного прогноза

150. Коэффициент Тейла является более точным показателем, чем
•

Видео:Коэффициент детерминации. Основы эконометрикиСкачать

Эконометрика (часть 1-1)

Решение промежуточных тестов
Выполнение практически (семинарских работ)
Решение итогового теста

ЕСЛИ У ВАС НЕ ПОЛУЧАЕТСЯ СДАТЬ ДАННЫЙ ПРЕДМЕТ ИЛИ НЕТ ВРЕМЕНИ, НАПИШИТЕ НАМ, ВЫПОЛНИМ БЫСТРО И НА ХОРОШУЮ ОЦЕНКУ. МЫ БОЛЕЕ 7 ЛЕТ ЗАНИМАЕМСЯ РЕШЕНИЕМ ТЕСТОВ И НАПИСАНИЕМ РАБОТ ДЛЯ ВАШЕГО ВУЗА.

Ниже указаны кнопки, нажмите на ту соц. сеть или месенджер, который Вы используете или заполните форму для того, чтобы мы ответили Вам на e-mail.

Чтобы написать через WhatsApp или Viber, данные приложения должны стоять у Вас на компьютере или войдите на сайт mum . zdai . ru с мобильного телефона, где стоят эти приложения, увидите мигающий круг онлайн консультанта, нажмите на него и выберите ту иконку месенджера, с которого желаете написать. В дальнейшем, мы останемся у Вас в списке чатов, можете писать сразу из месенжера.

Вопросы теста:

Если в уравнении регрессии увеличить x на единицу, то в результате этого yв среднем изменится на величину:
При исследовании зависимости себестоимости продукции y от объема выпуска x1 и производительности труда x2 по данным n=20 предприятий получено уравнение регрессии и среднеквадратические отклонения коэффициентов регрессии и . Можно ли при уровне значимости ?=0,05 утверждать, что знач имы коэффициенты
Что минимизируется согласно методу наименьших квадратов:
Переменные, которые формируются вне модели, называются
По данным n=25 регионов получена регрессионная модель объема реализации медикаментов на одного жителя у в зависимости от доли городского населения х1 и числа фармацевтов х2
на 10 тыс. жителей: и среднеквадратичное отклонение коэффициентов регрессии и Начиная с какого уровня значимости ? можно утверждать, что y зависит от доли городского населения х1 :
Свойства коэффициентов регрессии как случайных величин зависят от свойств ________ уравнения
При исследовании зависимости себестоимости продукции y от объема выпуска x1 и производительности труда x2
В чем состоит условие независимости погрешностей регрессионной модели :
Проверить гипотезу о гомоскедастичности регрессионных остатков можно с помощью:
В модели регрессионного анализа к распределению ошибок наблюдения , а именно к их математическому ожиданию и дисперсии предъявляются требования:
Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения , а именно к их математическому ожиданию и дисперсии .
Чему равна оценка дисперсии элемента b1 вектора b.
Эконометрический инструментарий базируется на методах и моделях
Если для случайных ошибок справедливо равенство для всех i=1,2,…,n, то это свидетельствует:
В чем состоит условие гомоскедастичности в регрессионной модели временного ряда, если :
При исследовании зависимости себестоимости продукции y от объема выпуска x1 и производительности труда x2
по данным n=20 предприятий получено уравнение регрессии и среднеквадратические отклонения коэффициентов регрессии: и . Определите с д оверительной вероятностью ?=0,99, на какую величину максимально может измениться себестоимость продукции y, если объем производства увеличить на единицу:
Статистика критерия для проверки значимости коэффициента регрессии имеет вид:
График выборочной автокорреляционной функции называется
Согласно методу наименьших квадратов для получения оценок b 0 и b 1 минимизируется:
В регрессионном анализе м_ат_ематическое ожидание _и дисперсия регрессионных остатков , отвечают следующим требованиям:
В чем условие гетероскедастичности в регрессионной модели временного ряда, если :
Если качественная независимая переменная принимает m значений, то необходимо определить:
По данным n=15 фирм исследована зависимость прибыли y от числа работающих x вида была получена оценка остаточной дисперсии и обратная матрица . Определите, чему равна дисперсия оценки коэффициента регрессии :
Параметр b в степенной модели является:
Трехшаговый метод наименьших квадратов – это метод:
Степень адекватности модели при оценки двухшаговым методом наименьших квадратов считается тем больше, чем:
Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии __________наблюдений
Модель скользящей средней имеет вид
Задача исследования зависимости одной зависимой переменной от нескольких объединяющих переменных решается с помощью
К нелинейным моделям по параметрам относятся модели
Если F-статистика Фишера превысит критическое значение F_крит, то регрессия считается
Стандартизованный коэффициент регрессии показывает
Стандартизованный коэффициент регрессии показывает
Стандартизованный коэффициент регрессии показывает
Необходимо исследовать зависимость между результатами письменных вступительных и курсовых экзаменов по математике. Получены следующие данные о числе решенных задач на вступительных экзаменах X (задание – 10 задач) и курсовых экзаменах Y (задания – 7 задач) 12 студентов, а также распределение этих студентов по фактору «пол»: Тогда линейная регрессивная модель Y по X с использованием фиктивной переменной по фактору пол имеет вид
№ студентаЧисло решенных задачПол студента№ студентаЧисло решенных задачПол студента
Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
Фиктивными называют переменные:
Статистической (или стохастической, вероятностной) получила название зависимость
Если для случайных ошибок справедливо равенство , для всех i=1,2,…,n, то это свидетельствует:
Верхнее число степеней свободы F-статистики в случае парной регрессии равно
Экономико-математическая модель становится эконометрической, если
Какое уравнение регрессии нельзя свести к линейному виду:
Корреляционной зависимостью между двумя переменными называется
Реальные экономические объекты, исследуемые с помощью эконометрических методов,описываются с помощью
Наиболее наглядным видом выбора уравнения парной регрессии является:
Выборочным уравнением регрессии называется уравнение
Коэффициент корреляции может принимать значения:
Остаточная сумма квадратов равна нулю:
Корреляционная зависимость может быть представлена в виде
Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
Добавление в уравнение множественной регрессии новой объясняющей переменной:
С помощью обратной матрицы определяется
С увеличением числа объясняющих переменных скорректированный коэффициентдетерминации: Для реализации двухшагового метода наименьших квадратов необходимо, чтобы:
Для получения эффективной оценки вектора b используют
Наилучший способ устранения автокорреляции – установление ответственного за нее фактора и включение соответствующей ___________ переменной в регрессию
Значение статистики Дарбина – Уотсона находится между значениями
Автокорреляция первого порядка – ситуация, когда случайный член Uк коррелирует с
Коэффициент a 1 уравнения вычисляется по формуле:
Уравнению регрессии соответствует множественный коэффициент корреляции . Какая доля вариации результативного показателя y (%) объясняется входящими в уравнение регрессии переменными х1 и х2 :
Свойство постоянства дисперсий ошибок регрессии называется гомоскедастичностью,Классическая нормальная линейная регрессионная модель имеет вид
Какое из уравнений является степенным:
Модельным уравнением регрессии называется уравнение
Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R 2 для модели парной регрессии равен
Суть коэффициента детерминации состоит в следующем:
Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
Переменная Y, имеющая при заданных значениях факторов некоторое распределение называется
С помощью обратной матрицы определяется
С помощью обратной матрицы определяется
Множественный коэффициент корреляции . Определите, какой процент дисперсии зависимой переменной объясняется влиянием факторов x1 и x2:
Если для случайных ошибок справедливо равенство для всех i=1,2,…,n, то это свидетельствует:
Уравнением линейной парной регрессии является уравнение:
На экзамене в группе из 15 студентов 4 человека получили отличную оценку, 8 человек- оценку хорошо, 3 человека – оценку удовлетворительно. Средний бал по группе равен:
На основании наблюдений за 50 семьями построено уравнение регрессии y =284,56+0,672 x где y – потребление, x – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
Временным динамическим рядом называется выборка наблюдений, в которой важны
Параметр называется __________, если косвенный метод наименьших квадратов дает несколько его оценок
Уравнение регрессии линейное, если
Суть коэффициента детерминации состоит в следующем:
Пусть имеются условные данные о средних расходах на конечное потребление (yt , денежных единиц) за 8 лет. Эконометрическая модель имеет вид Коэффициент a 1 уравнения равен своему математическому ожиданию, если:
По данным таблицы найдите уравнение регрессии Y по XМодель множественной регрессии можно представить в виде
Модель распределенных лагов имеет вид
Модель авторегрессии и распределенных лагов имеет вид
Какое из следующих уравнений нелинейно по оцениваемым параметрам:
Границы интервальной оценки свободного члена уравнения регрессии отстоят от точечной оценки на величину, не превышающую:
В хорошо подобранной модели остатки должны (выберите необходимые пункты):
Коэффициент a₁ уравнения Y_i = a ₀ + a ₁ X_i + e_t равен своему математическому ожиданию, если:
Уравнению регрессии соответствует множественный коэффициент корреляции . Какая доля вариации результативного показателя y (%) объясняется входящими в уравнение регрессии переменными х1 и х2 :
При исследовании зависимости себестоимости продукции y от объема выпуска x1 и производительности труда x2
по данным n=20 предприятий получено уравнение регрессии и среднеквадратические отклонения коэффициентов регрессии: _{и .} увеличить на 1%, учитывая при этом, что _:

Выборочный частный коэффициент корреляции вычисляется по формуле Скорректированный коэффициент детерминации: Приведенная форма системы одновременных уравнений имеет вид:
Если при оценке __________ уравнения в качестве инструментальных переменных используются экзогенные переменные, то получаемые при этом оценки совпадают с оценками косвенного метода наименьших квадратов Коэффициент a₁ уравнения Y_i = a ₀ + a ₁ X_i + e_t вычисляется по формуле:
Для решения одновременных уравнений применяется
Коэффициент детерминации при двухшаговом методе наименьших квадратов может быть:
Кейнсианская модель формирования доходов является
МНКдает__________дляданнойвыборкизначениекоэффициентадетерминацииR2
Мультипликативнаястепеннаямодельлегкосводитсяклинейнойпутем___________обеихчастейуравнения
С помощью обратной матрицы определяется
Сувеличениемчислаобъясняющихпеременныхскорректированныйкоэффициентдетерминации:
F-статистика для____________является вточности квадратом t-статистики дляrx,y
Привысокомуровнезначимостипроблемазаключаетсяввысокомрискедопущения
Поданным таблицы коэффициент эластичности равен
Граничноезначениеобластипринятиягипотезысp%-нойвероятностьюсовершитьошибкуIродаопределяется__________приp-процентномуровнеСкорректированныйкоэффициентдетерминациивычисляетсяпоформуле
Стандартизованные коэффициенты регрессии:
Явление, когда строгая линейная зависимость между переменными приводит к невозможности применения МНК, называется
Для функции Кобба-Дугласа у=100k 1/3 ×i 2/3 эластичность выпуска продукции по капиталу равна
Для функции Кобба-Дугласа у=100k1/3?i2/3 эластичность выпуска продукции по капиталу равна
Модель оказывается с математической точки зрения предпочтительней модели , если выполняется условие
Если , то значение a 1 будет:
Если , то значение a 1 будет:
Уравнение идентифицируемо, если:
Приведенная форма Кейнсианской модели имеет вид
Лаговые переменные – это:
Уравнение неидентифицируемо, если:
Общий вид системы одновременных уравнений представляется в матричной форме как
Тождества, которые содержатся в системе одновременных уравнений, имеют вид:
Для определения параметров сверхидентифицируемой модели:
Модель идентифицируема, если:
Второе условие Гаусса – Маркова предполагает, что дисперсия случайного члена __________ в каждом наблюдении
Для определения параметров неидентифицируемой модели:
Приведенная система одновременных уравнений имеет вид: Если система идентифицируема, и количество экзогенных переменных Х совпадает с количеством эндогенных переменных Y, оценки двушагового метода совпадают с оценками ___________ метода наименьших квадратов
Экономический временной ряд – это ряд, который
В модели множественной регрессии за изменение _________ регрессии отвечает несколько объясняющих переменных
Временной ряд в виде аддитивной модели имеет вид
Модель с распределением Койка лаговых объясняющих переменных имеет вид
Поправка Прайса – Уинстена – метод спасения ________________ в автокорреляционной схеме первого порядка
Прогноз развития на основе экстраполяция временных рядов является эффективным в рамках _________ периода прогнозирования
Временной (динамический) ряд имеет вид
Временной (динамический) ряд имеет вид
Автоковариация k-го порядка временного ряда Yt вычисляется по формуле
Модель авторегрессии возмущения или автокорреляция временного ряда имеет вид
Третье условие Гаусса – Маркова состоит в том, что cov(ui,uj) = 0, если Мультипликативная степенная модель легко сводится к линейной путем ___________ обеих частей уравнения Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно: Граничное значение области принятия гипотезы с p%-ной вероятностью совершить ошибку I рода определяется __________при p-процентном уровне значимости
При высоком уровне значимости проблема заключается в высоком риске допущения
Для построения модели линейной множественной регрессии вида y = a + b ₁ x ₁ + b ₂ x ₂ необходимое количество наблюдений должно быть не менее:
Для построения модели линейной множественной регрессии вида необходимое количество наблюдений должно быть не менее:
Для построения модели линейной множественной регрессии вида необходимое количество наблюдений должно быть не менее:
Множественный коэффициент корреляции . Определите, какой процент дисперсии зависимой переменной объясняется влиянием факторов x1 и x2:
Второе условие Гаусса – Маркова заключается в том, что
Коэффициент детерминации определяется по формуле
Скорректированный коэффициент детерминации вычисляется по формуле
При выборе спецификации модели следует руководствоваться ________ анализом
Структурный параметр называется _________, если он может быть однозначно оценен с помощью косвенного метода наименьших квадратов
В двухшаговом методе наименьших квадратов оценки обладают свойствами:
Уравнение сверхидентифицируемо, если:
Функция Кобба – Дугласа имеет вид Y =
Модель оказывается предпочтительней модели _______, если скорректированный коэффициент детерминации при удалении регрессоров Z увеличивается
Системы одновременных или регрессионных уравнений используются, когда
Тест Чоу применяют:
Гетероскедастичность ошибок в регрессионных моделях означает, что они имеют:
По данным n=15 фирм исследована зависимость прибыли y от числа работающих x вида была получена оценка остаточной дисперсии и обратная матрица Определите, чему равна при доверительной вероятности ?=0.95 верхняя граница интервальной оценки коэффициента регрессии при х :
По данным n=15 фирм исследована зависимость прибыли y от числа работающих x вида была получена оценка остаточной дисперсии и обратная матрица Определите, чему равна при доверительной вероятности γ=0.95 верхняя граница интервальной оценки коэффициента регрессии при х :
Для моделей с переменной структурой характерно следующее:
Могут ли фиктивные переменные применяться для моделирования сезонных колебаний:
Границы интервальной оценки коэффициента регрессии отстоят от точечной оценки на величину, не превышающую:
Если в уравнении регрессии увеличить x на единицу, то в результате этого yв среднем изменится на величину:

Среднее арифметическое значения временного ряда имеет вид
Производственная функция Кобба-Дугласа имеет вид
Мультиколлинеарность в эконометрических исследованиях чаще проявляется
Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
Стандартизованные коэффициенты регрессии β _i :
По таблице найти скорректированный коэффициент детерминации

Переменные, формирующие внутри функционирования объекта, называются
Для получения достоверных данных о распределении какой-либо случайной величины, необходимо иметь
Набор показателей экономических переменных, полученных в данный момент времени называются
Качество модели из относительных отклонений по каждому наблюдению оценивает:
Если случайная величина принимает значения Х1….,Хn с вероятностями Р1. Рn соответственно, то математическое ожидание случайной величины —
Коэффициент корреляции может принимать значения:
Коэффициент корреляции r_xy может принимать значения: На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:
Модель с распределением Койка лаговых объясняющих переменных оценивается с помощью
Временной ряд в виде мультипликативной модели имеет вид
Экономический временной ряд отличается от технологического тем, что
Статические характеристики временного лага
Аддитивная модель временного ряда строится, если:
Модель авторегрессии и проинтегрированного скользящего среднего имеет вид
Мультипликативная модель временного ряда строится, если:
Функция Кобба – Дугласа называется
Модель сосредоточенного лага имеет вид
Тесты на гетероскедастичность – это
Для регрессии второго порядка y= 12+7x₁-3x₂ отклонение от регрессии наблюдения (х₁=2, х₂=1, y=20) равно
При проведении теста Голдфелда – Квандта из рассмотрения исключаются ______ наблюдений
Временной лаг — это При применении взвешенного метода наименьших квадратов используется формула
Модель авторегрессии и скользящей средней имеет вид
Дисперсия временного ряда вычисляется по формуле
Авторегрессионная модель первого порядка имеет вид
Модели временных рядов – это
График зависимости автокорреляционной функции временного ряда от величины лага называется
Автокорреляция k-го порядка временного ряда Yt — коэффициент корреляции вычисляется по формуле
Для модели потребления Фридмена могут быть применены
Коэффициент автокорреляции для таблицы по 6-ти пар наблюдений

Число степеней свободы для t-статистики равно числу наблюдений в выборке __________ количество оцениваемых коэффициентов
При использовании уровня значимости, равного 5%, истинная гипотеза отвергается в _____ случаев
Стандартное отклонение оценки b для параметра β вычисляется по формуле
Утверждение о том, что неизвестный параметр модели принадлежит заданному множеству А, называется
Точность оценок по МНК улучшается, если увеличивается
Оценка стандартного отклонения случайной величины, полученная по данным выборки, называется стандартной ___________ случайной величины
Эксперимент по методу Монте-Карло – искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных
Оценивание каждого параметра в уравнении регрессии поглощает _________ свободы в выборке
Второй шаг метода Зарембки заключается в пересчете наблюдений y в новые
По данным таблицы коэффициент эластичности равенЕсли наблюдаемое значение F-статистики при тестировании гипотезы оказывается меньше 1, то модель ______ оказывается предпочтительнее чем, модель
Если наблюдаемое значение F-статистики при тестировании гипотезы y = 0 оказывается меньше 1, то модель ______ оказывается предпочтительнее чем, модель Y = X β + Zy +ɛ
Экзогенные переменные – это:
Если ∑( X_i ɛ _i ) ≠ 0, то значение a₁ будет:
Отличия экзогенных переменных от эндогенных заключается в том, что они
Наибольшее распространение в эконометрических исследованиях получили:
Проблема, связанная со смещением оценки коэффициентов регрессии, в одном случае, или с утратой эффективности этих оценок в другом случае неправильной спецификации переменных, перестает существовать, если коэффициент парной корреляции между переменными равен
Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина – Уотсона
Модель сверхидентифицируема, если:
Эффективная процедура оценивания систем регрессионных уравнений сочетает метод одновременного оценивания и метод интсрументальных переменных, и при этом называется
Параметр, для которого существует несколько способов выражения через коэффициенты приведенной формы, называется
Переменные, которые формируются внутри модели называются
структурный параметр называется ___________, если его значение невозможно получить, даже зная точные значения параметров приведенной формы
Для определения параметров точно идентифицируемой модели:
Модель неидентифицируема, если:
Тест ранговой корреляции Спирмена – тест на
Фиктивную переменную для коэффициента наклона вводят как ____________ фиктивной переменной, отвечающей за исследуемую категорию, и интересующей нефиктивной переменной
Автокорреляция – нарушение ___________ условия Гаусса – Маркова
Эндогенные переменные – это:
Аддитивная модель временного ряда имеет вид:
На первом этапе применения теста Голдфелда – Квандта в выборке все наблюдения
Авторегрессионная модель скользящей средней порядков p и q соответственно имеет вид
Тесты по определения автокорреляции между соседними членами – это
В обобщенной линейной модели в отличие от классической модели ковариация и дисперсия объясняющих переменных могут быть
На основе поквартальных данных построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 0,8 – I квартал, 1,2 – II квартал и 1,3 – III квартал. Значение сезонной компоненты за IV квартал есть:
Использование автокорреляционных остатков
Члены временного ряда __________ одинаково распределенными
Построение аддитивной и мультипликативной моделей сводится к расчету значений
Модель скользящей средней q-го порядка имеет вид
Мультипликативная модель временного ряда имеет вид: Критерий Дарбина-Уотсона применяется для:
Коэффициент, который измеряет корреляцию между членами одного и того же ряда называется Коэффициент автокорреляции:
Число периодов, по которым рассчитывают коэффициент автокорреляции называется Метод наименьших квадратов — метод нахождения оценок параметров регрессии, основанный на минимизации _______ квадратов остатков всех наблюдений
Переменные, задаваемые извне называются Значимость уравнения регрессии в целом оценивает: Коэффициент наклона в уравнении линейной регрессии показывает ___________изменяется y при увеличении x на одну единицу
Эффективная оценка – несмещенная оценка, имеющая ______________ среди всех несмещенных оценок Необходимость применения специальных статистических методов для обработки экономической информации вызвана ________ данных
Всю совокупность реализаций случайной величины называют __________совокупностью
Объясняющие переменные могут считаться детерминированными, если они принимают
Некоррелированность возмущений независимых случайных величин выражается уравнением
Для функции y = a + b / x + ε средний коэффициент эластичности имеет вид:
Для функции средний коэффициент эластичности имеет вид:
Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют____________________
Стандартное отклонение случайной величины характеризует среднее ожидаемое расстояние между наблюдениями этой случайной величины и ее
Классический метод к оцениванию параметров регрессии основан на:
Задачами регрессионного анализа являются
Мерой разброса значений случайной величины служит
Значение оценки является ____________
Коэффициент линейного парного уравнения регрессии:
В эконометрической модели объясненная часть – это
По данным таблицы коэффициент корреляции равен

Логарифмическое преобразование позволяет осуществить переход от нелинейной модели y = 5x2u к модели
Критерий Г. Чоу может быть использован при построении регрессионных моделей при воздействии ________________ признаков
При вычислении t-статистики применяется распределение____________
Показатель выборочной ковариации позволяет выразить связь между двумя переменными
Для функции y = 4x 0,2 , эластичность равна_________
Способ оценивания (estimator) – общее правило для получения _____________ какого-либо параметра по данным выборки
Невыполнение 2 и 3 условий Гаусса – Маркова, приводит к потере свойства_________оценок
При использовании метода Монте-Карло результаты наблюдения генерируются с помощью :
Тест Бокса – Кокса (решетчатый поиск) – прямой компьютерный метод выбора наилучших значений ______________ модели в заданных исследователем пределах с заданным шагом (решеткой):
Если из экономических соображений известно, что β ≥ β₀ , то нулевая гипотеза отвергается только при
t-статистика для коэффициента корреляции r определяется как
По четырем предприятиям региона (см. табл.) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов х₂(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х₁ (%), тогда уравнение множественной регрессии имеет вид

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Ответы по гос эконометрике

Автор работы: Пользователь скрыл имя, 06 Декабря 2010 в 11:53, шпаргалка

Описание

Ответы на 8 вопросов по экономическому моделированию.

Работа состоит из 1 файл

Видео:Расстановка коэффициентов в окислительно-восстановительных реакцияхСкачать

Эконометрика.doc

Спецификация экономических моделей

Парная линейная регрессия

Линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием М(Y ½ X=x_i) зависимой переменной Y и одной объясняющей переменной X (x_i — значения независимой переменной в i-ом наблюдении, i = l, 2, . n).

Для отражения того факта, что каждое индивидуальное значение y_i отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (3.5) случайное слагаемое e _i,

Соотношение (3.6) называется теоретической линейной регрессионной моделью; b ₀ и b ₁ — теоретическими параметрами (теоретическими коэффициентами) регрессии; e _i — случайным отклонением.

Следовательно, индивидуальные значения y_i представляются в виде суммы двух компонент: систематической ( b ₀ + b ₁ × x_i) и случайной ( e _i). В общем виде теоретическую линейную регрессионную модель будем представлять в виде

Задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным (x_i, у_i, i = 1, 2, . n) для переменных X и Y:

а) получить наилучшие оценки неизвестных параметров b ₀ и b ₁;

б) проверить статистические гипотезы о параметрах модели;

в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии

где y_теор(x_i) — оценка условного математического ожидания M(Y ÷ Х = x_i);

a_* и b_* — оценки неизвестных параметров b ₀ и b ₁, называемые эмпирическими (выборочными) коэффициентами регрессии. Следовательно, в конкретном случае

где отклонение e_i — оценка теоретического случайного отклонения e _i.

Коэффициенты a_* и b_* эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации одной из следующих сумм:

Однако первая сумма не может быть мерой качества найденных оценок в силу того, что существует бесчисленное количество прямых (в частности, Y = у_ср), для которых S e_i = 0.

Метод определения оценок коэффициентов из условия минимизации второй суммы называется методом наименьших модулей (МНМ).

Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется третья сумма. Он получил название метод наименьших квадратов (МНК). Среди других методов определения оценок коэффициентов регрессии отметим метод моментов (ММ), метод максимального правдоподобия (ММП) и метод центра неопределённости (МЦН).

Парная нелинейная регрессия

Нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства — трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и др.

Могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.

Все нелинейные регрессии делятся на два класса:

1) регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам:

полиномы разных степеней

2) регрессии, нелинейные по оцениваемым параметрам:

Модель множественной регрессии

Множественная регрессия – это уравнение статистической связи с несколькими независимыми переменными:

где y — зависимая переменная (результативный признак);

x₁, x₂, …, x_p – независимые переменные (факторы). Все эти переменные входят в уравнение (5.1) с некоторыми коэффициентами.

Возможны разные виды уравнения множественной регрессии, чаще используются следующие функции: линейные и нелинейные.

В линейной множественной регрессии коэффициенты при х_i характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменных значениях других факторов, закреплённых на среднем уровне.

При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности к потреблению. Например, если функция потребления С_t имеет вид С_t = b₀ + b₁* R_t + b₂* R_t-1 + e _t, то потребление за t-й период времени зависит от дохода того же периода R_t и от дохода предшествующего периода R_t-1. Соответственно, коэффициент b₁ характеризует эффект от единичного возрастания дохода R_t при неизменном уровне предыдущего дохода. Коэффициент b₁ обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на величину b = b₁+b₂. Коэффициент b рассматривается здесь как долгосрочная предельная склонность к потреблению.

Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления C_t-1:

В этом уравнении параметр b₁ также характеризует краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода. Долгосрочная предельная склонность к потреблению имеет вид b₁/(1- b₂).

В степенной функции y_теор(x₁,x₂,…,x_p) = a × x1 b1 × x2 b2 × … × xp bp коэффициенты b1, b2, …, bp являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

2.Понятие корреляции. Виды коэффициентов корреляции, экономический смысл их определения

Корреляция — вероятностная или статистическая зависимость, не имеющая строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия. В случае корреляционной зависимости, изменение одной случайной величины приводят к изменению среднего значения другой случайной величины. Особенность корреляции состоит в том, что связи обнаруживаются не в единичных случаях, а в массовых явлениях, следовательно, необходимо иметь как можно больше объектов наблюдения.

Корреляция рассчитывается по формуле:

(1) — математическое ожидание х, — математическое ожидание y. (Математическое ожидание – среднее значение случай величины.)

cov (x,y) – ковариация переменных (ковариация определяет меру взаимодействия двух случайных переменных)

σ_x – стандартное отклонение x; σ_y – стандартное отклонение y.

D(x) – дисперсия случайной величины х; D(y) – дисперсия случайной величины y. Дисперсия характеризует отклонение (разброс, рассеяние) значений случайной величины относительно среднего значения.

Формулу (1) можно представить в виде:

Коэффициенты корреляции бывают следующих видов:

1)парные коэффициенты корреляции

2)частные коэффициенты корреляции

3)коэффициенты множественной корреляции.

Парные коэффициенты корреляции используются для измерения тесноты связи между двумя переменными без учета их взаимодействия с другими переменными. Например,

С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов. В связи с этим возникают два типа задач: задачи измерения комплексного влияния на результативную переменную нескольких переменных и задачи определения тесноты связи между двумя переменными при фиксированных значениях остальных переменных. Задачи первого типа решаются с помощью множественных коэффициентов корреляции, задачи второго типа — с помощью частных коэффициентов корреляции.

Частный, или чистый, коэффициент корреляции между двумя признаками (х и y) при исключении влияния третьего признака (z) рассчитывается по формуле:

остаточная дисперсия(остаточная сумма квадратов) = S2

Если выразить остаточную дисперсию через показатель детерминации S2 остат = s 2у*(1 — r2), то формула коэффициента частной корреляции примет вид:

В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: y= a+b1*x1+ b2*x2+ b3*x3

Коэффициент частной корреляции, измеряющий влияние на у фактора хi, при неизменном уровне других факторов, можно определить по формуле